辛普森公式求函数的近似积分【通用计算】
利用辛普森公式可以近似求出复杂函数的积分值,公式如下:
∫ a b f ( x ) d x ≈ h 3 [ y 0 + y 2 n − 1 + 4 ( ∑ i = 1 n − 1 y 2 i − 1 ) + ∑ i = 1 n − 1 y 2 i ] \int_{a}^{b} f(x) dx \approx \frac{h}{3}\left[ y_0 + y_{2n-1} + 4(\sum\limits_{i=1}^{n-1} y_{2i-1}) + \sum\limits_{i=1}^{n-1} y_{2i} \right] ∫abf(x)dx≈3h[y0+y2n−1+4(i=1∑n−1y2i−1)+i=1∑n−1y2i]
其中 y 0 y_0 y0 到 y 2 n − 1 y_{2n-1} y2n−1的值是原函数在等分点上的函数值。
下面是一个简单的示例:
import numpy as npdef calculate_simpson_integral(target_fun, left_zone, right_zone, zone_num):""" 使用辛普森规则计算积分近似值 """# 计算区间的步长step_len = (right_zone - left_zone) / zone_num# 在区间上生成 zone_num+1 个等距的点dots = np.linspace(left_zone, right_zone, zone_num + 1)# 求分段点的函数值fun_values = target_fun(dots)# 利用公式求近似积分值return step_len / 3 * (fun_values[0] + fun_values[-1] +4 * np.sum(fun_values[1:-1:2]) +2 * np.sum(fun_values[2:-2:2]))# 测试
def integral_function(x):""" 定义被积函数"""return x ** 2# 定义区间参数和分区数量
left_zone = 0
right_zone = 1
zone_num = 100
result = calculate_simpson_integral(integral_function, left_zone, right_zone,zone_num)print("定积分的近似值为:", result)你可以根据实际需要定义被积函数,然后利用calculate_simpson_integral求其在指定区间上的积分值。
相关文章:

辛普森公式求函数的近似积分【通用计算】
利用辛普森公式可以近似求出复杂函数的积分值,公式如下: ∫ a b f ( x ) d x ≈ h 3 [ y 0 y 2 n − 1 4 ( ∑ i 1 n − 1 y 2 i − 1 ) ∑ i 1 n − 1 y 2 i ] \int_{a}^{b} f(x) dx \approx \frac{h}{3}\left[ y_0 y_{2n-1} 4(\sum\limits_{i1…...

即插即用 | YOLOv8热力图可视化方法详解,揭秘AI如何「看」世界!【附完整源码】
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...
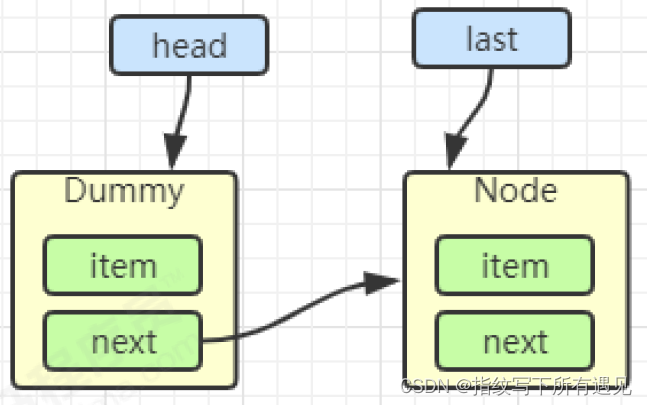
多线程学习D10 收尾了应该
线程安全集合类概述 重点介绍java.util.concurrent.* 下的线程安全集合类,可以发现它们有规律,里面包含三类关键词:Blocking、CopyOnWrite、Concurrent Blocking 大部分实现基于锁,并提供用来阻塞的方法 CopyOnWrite 之类容器修改…...

ai可以做思维导图吗?当然是可以的!
ai可以做思维导图吗?在快节奏的现代生活中,思维导图作为一种高效的信息组织和表达工具,越来越受到人们的青睐。随着人工智能(AI)技术的不断发展,AI思维导图软件也应运而生,它们不仅能够帮助用户…...

景源畅信数字:抖音小店的入住门槛大不大?
近年来,随着短视频平台的崛起,抖音小店逐渐成为了众多商家和创业者关注的焦点。那么,抖音小店的入住门槛究竟大不大呢?本文将从四个方面对这一问题进行详细阐述。 一、注册流程 抖音小店的注册流程相对简单,只需按照官方指引完成…...
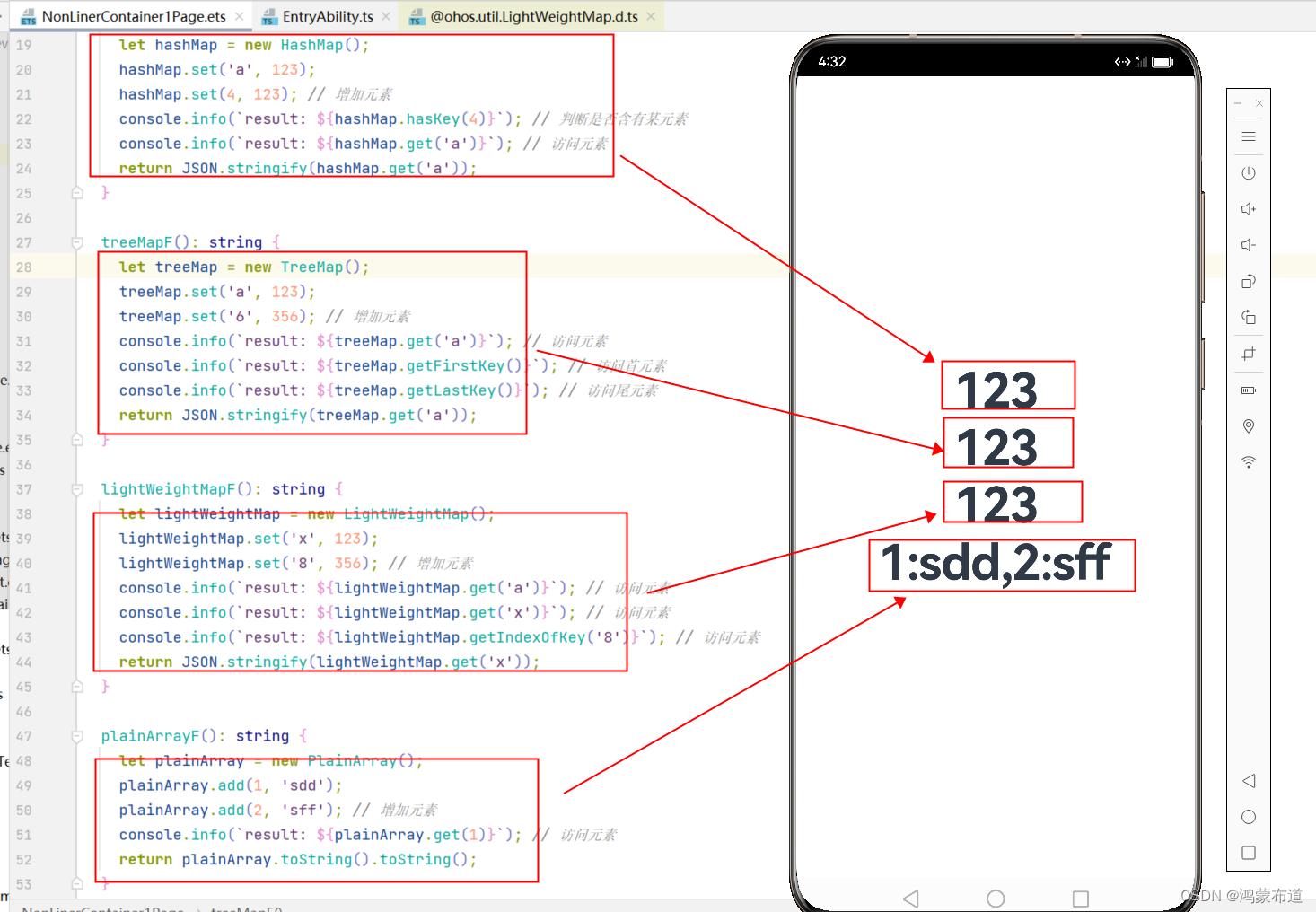
鸿蒙开发-ArkTS语言-容器-非线性容器
鸿蒙开发-UI-web 鸿蒙开发-UI-web-页面 鸿蒙开发-ArkTS语言-基础类库 鸿蒙开发-ArkTS语言-并发 鸿蒙开发-ArkTS语言-并发-案例 鸿蒙开发-ArkTS语言-容器 文章目录 前言 一、非线性容器 1.HashMap 2.HashSet 3.TreeMap 4.TreeSet 5.LightWeightMap 6.LightWeightSet 7.P…...

【C语言】指针篇- 深度解析Sizeof和Strlen:热门面试题探究(5/5)
🌈个人主页:是店小二呀 🌈C语言笔记专栏:C语言笔记 🌈C笔记专栏: C笔记 🌈喜欢的诗句:无人扶我青云志 我自踏雪至山巅 文章目录 一、简单介绍Sizeof和Strlen1.1 Sizeof1.2 Strlen函数1.3 Sie…...

【设计模式】单例模式的前世今生
文章目录 引言简介起航!向“确保某个类在系统中只有一个实例”进发 ⛵️Lazy SingletonDouble-checked locking(DCL) SingletonVolatile SingletonAtomic SingletonMeyers Singleton 附:C静态对象的初始化 引言 说起单例模式&…...

厦门网上在线教育系统,线下老师怎么转型到线上网上授课?
现在很多 线下老师都想转到线上做网课,但是在转线上过程中会出现很多问题,很多人都不知道怎么开始,今天小编和大家说一下要注意的。 一、你要有一套适合线上的教学视频 首先你要准备做的课程内容是什么,怎么讲,讲什么&…...
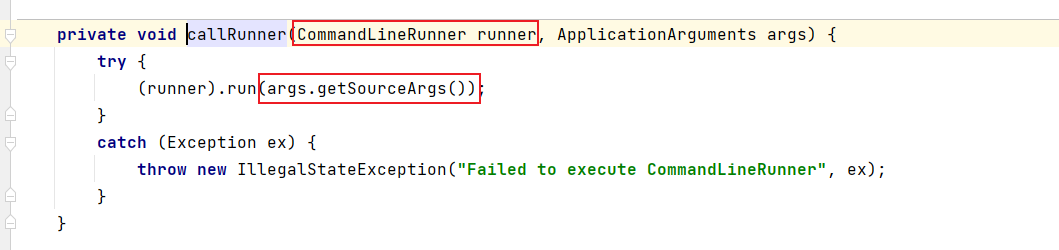
Spring底层入门(九)
boot的执行流程分为构造SpringApplication对象、调用run方法两部分 1、Spring Boot 执行流程-构造 通常我们会在SpringBoot的主启动类中写以下的代码: 参数一是当前类的字节码,参数二是main的args参数。 public class StartApplication {public static…...
)
掌握Android Fragment开发之魂:Fragment的深度解析(下)
在上一篇文章中,我们深入探讨了Fragment 通信,包含Fragment 向 Activity 传递数据、Activity 向 Fragment 传递数据、Fragment 之间的通信方式。感兴趣的朋友,请前往查阅: 掌握Android Fragment开发之魂:Fragment的深度…...
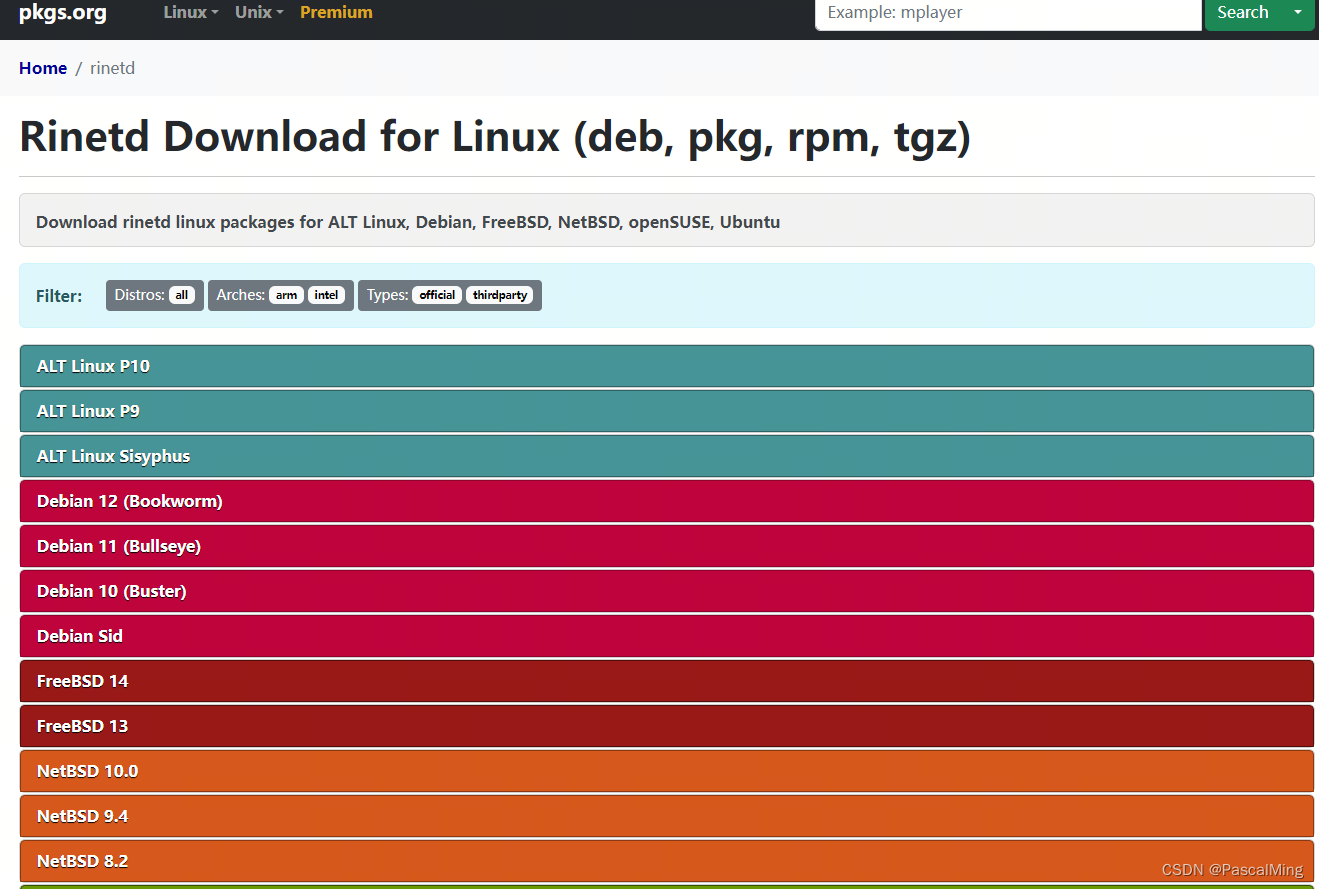
小巧简单实用的Linux端口转发工具Rinetd
Linux下实现端口转发有很多种方法,尤其是在可以联网的情况下,更是容易。最近在资源受限的定制系统中,找到一个方便离线安装和使用的端口转发工具Rinetd,安装包仅几十K,而且有很多版本的Linux发行系统的支持。 1、安装…...

HackBar 新手使用教程(入门)
啥是Hackbar? Hackbar是一个Firefox 的插件,它的功能类似于地址栏,但是它里面的数据不受服务器的相应触发的重定向等其它变化的影响。 有网址的载入于访问,联合查询,各种编码,数据加密功能。 这个Hackbar可以帮助你在测试SQL注入,XSS漏洞和网站的安全性,主要是帮助…...

<Linux> 权限
目录 权限人员相对于文件来说的分类更改权限文件的拥有者与所属组umask粘滞位 权限 权限是操作系统用来限制对资源访问的机制,权限一般分为读、写、执行。系统中的每个文件都拥有特定的权限、所属用户及所属组,通过这样的机制来限制哪些用户、哪些组可以…...

Nacos Docker 快速部署----解决nacos鉴权漏洞问题
Nacos Docker 快速部署 1. 说明 1.1 官方文档 官方地址 https://nacos.io/zh-cn/docs/v2/quickstart/quick-start.html docker启动文件的gitlhub地址 https://github.com/nacos-group/nacos-docker.git 问题: 缺少部分必要配置与说明 1.2 部署最新版本Nacos&…...
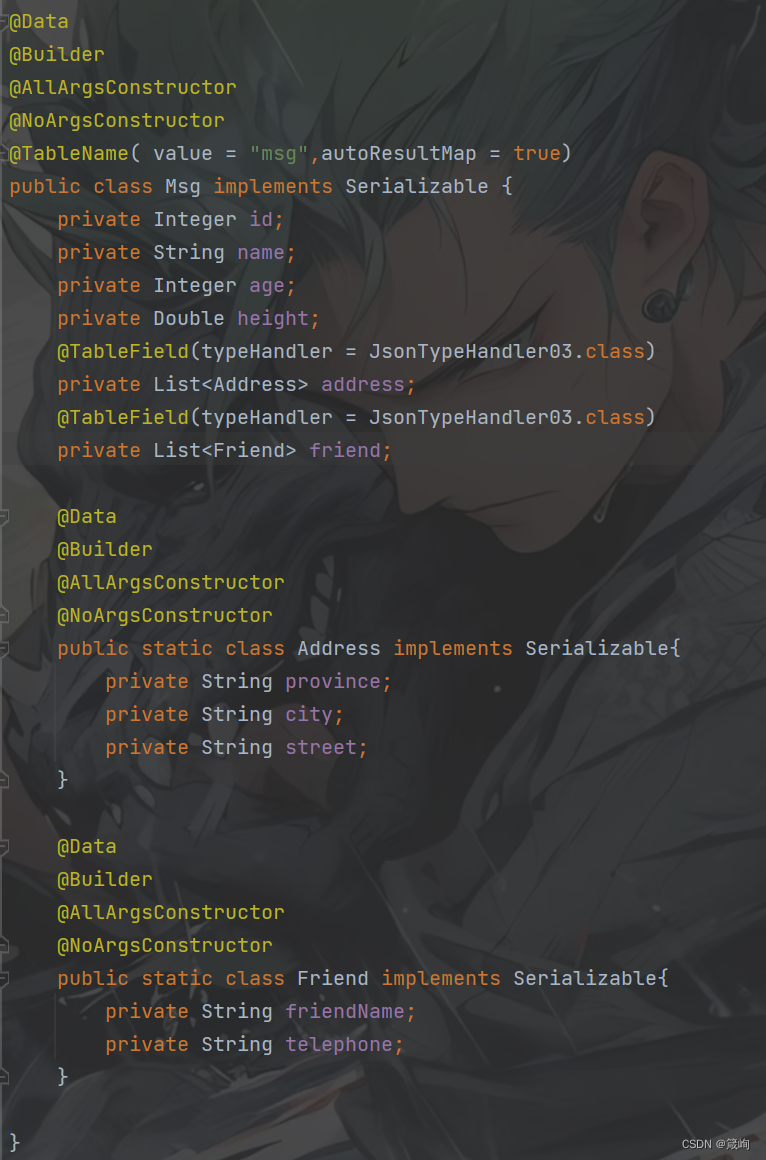
存储或读取时转换JSON数据
一、 数据库类型 二、使用Hutool工具 存储时将数据转换为JSON数据 获取时将JSON数据转换为对象 发现问题: 原本数据对象是Address 和 Firend但是转换完成后数据变成了JSONArray和JSONObject 三、自定义TypeHandler继承Mybatis的BaseTypeHandler处理器 package …...

Spring Data JPA的作用和用法
Spring Data JPA 是 Spring 框架的一个模块,它提供了一种数据访问抽象,允许以一种声明式和简洁的方式来处理数据库操作。它基于 Java Persistence API (JPA),是一个行业标准的 ORM(对象关系映射)规范,用于将…...
【go项目01_学习记录08】
学习记录 1 模板文件1.1 articlesStoreHandler() 使用模板文件1.2 统一模板 1 模板文件 重构 articlesCreateHandler() 和 articlesStoreHandler() 函数,将 HTML 抽离并放置于独立的模板文件中。 1.1 articlesStoreHandler() 使用模板文件 . . . func articlesSt…...

Java中的线程
一、创建线程的几种方式? ① 通过继承Thread类并重写run方法 ,实现简单但不可以继承其他类 Thread底层也是实现了Runnable接口,重写的是run而不是start方法 ②实现Runnable接口并重写run方法, 避免了单继承的局限性ÿ…...
(完整代码))
顺序表的实现(迈入数据结构的大门)(完整代码)
seqlist.h #pragma once typedef int SLDataType;#include<stdio.h> #include<stdlib.h> #include<assert.h>typedef struct SeqList {SLDataType* a;int size; // 有效数据个数int capacity; // 空间容量 }SL;//初始化和销毁 void SLInit(SL* ps); void SL…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
