Java 7大排序
🐵本篇文章将对数据结构中7大排序的知识进行讲解

一、插入排序
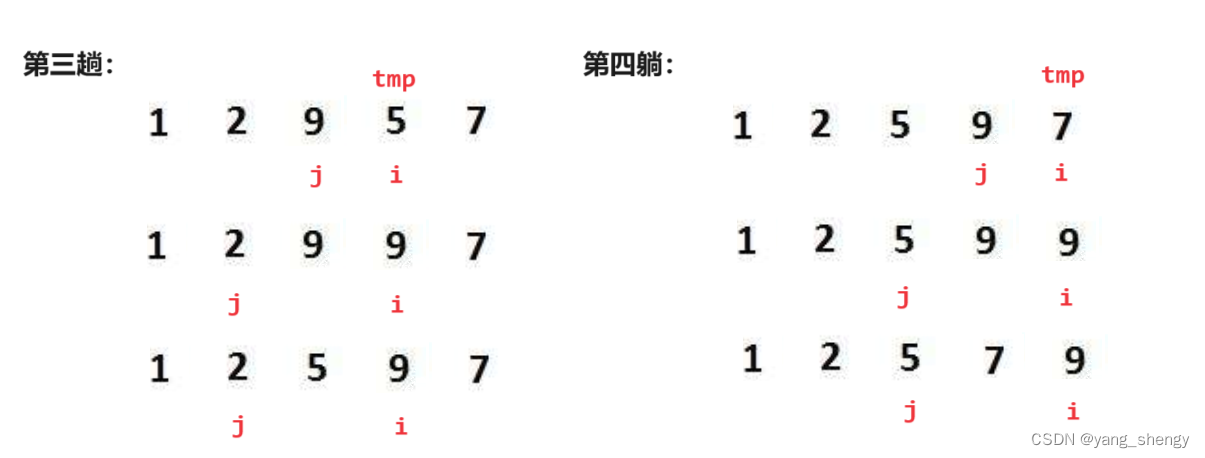
有一组待排序的数据array,以升序为例,从第二个数据开始(用tmp表示)依次遍历整组数据,每遍历到一个数据都再从tmp的前一个数据开始(下标用j表示)从后往前依次和其进行比较,如果tmp比它小,则令array[j + 1] = array[j];
1.1 实例讲解
第一趟:

第二趟:

第三趟和第四躺:
1.2 代码实现
public void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (tmp < array[j]) {array[j + 1] = array[j]; //将tmp移动到当前数据顺序的最小位置处,此步操作相当于给tmp腾位置} else {break;}}array[j + 1] = tmp;}}
在该排序算法中,当tmp前面出现比其小的元素时,则再往前的数据也一定比tmp小,所以插入排序是元素越有序,其效率越快的排序算法
时间复杂度:O(N²)
空间复杂度:O(1)
稳定
二、希尔排序
希尔排序是对直接插入排序的优化,它会将一组数据进行分组,然后针对每一组进行直接插入排序,那么该如何进行分组:定义一个gap,代表同一组数据的间隔,比如由一组数据:6,5,4,3,2,1;gap = 2,则6,4,2为一组,5,3,1为一组。在gap = 2的情况下的每一组数据排序完毕后,要缩小gap并再进行分组,然后再对每一组进行插入排序,随着gap的减小,该组数据会变得越来越有序,当gap = 1时,此时数据已经接近有序了,所以效率会非常快
2.1 实例讲解
第一躺:
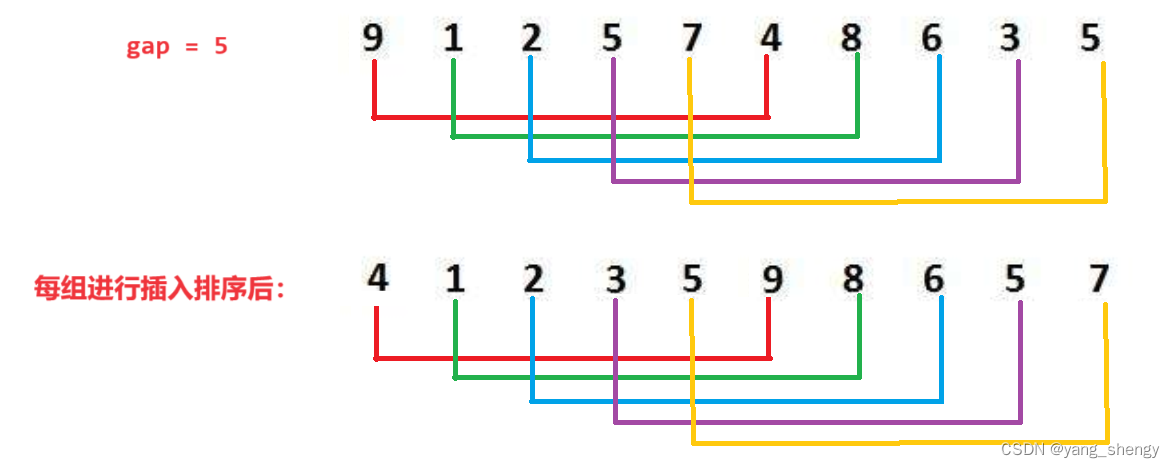
第二趟:
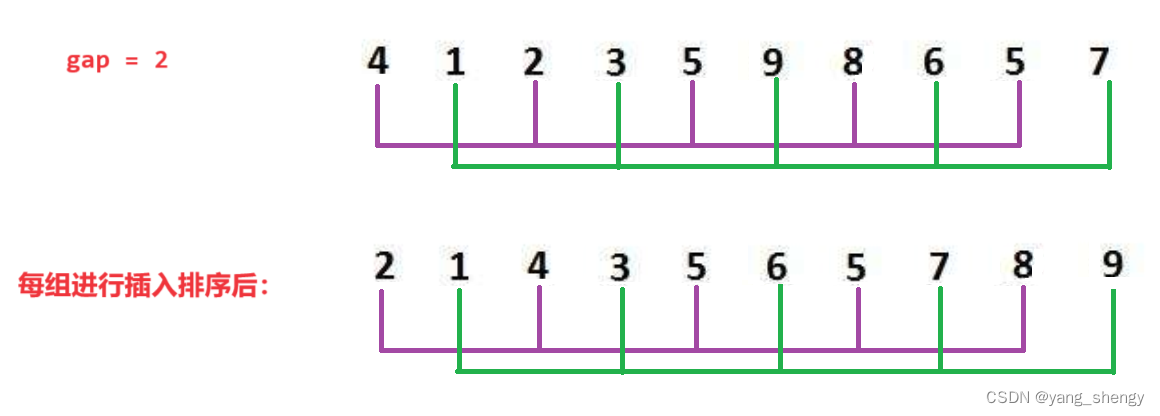
第三趟:

2.2 代码实现
public void shellSort(int[] array) {int gap = array.length;while(gap > 1) { //当gap = 1时分组结束gap = gap / 2;shell(array, gap);}}private void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (tmp < array[j]) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}
希尔排序不稳定
三、选择排序
选择排序较为简单,这里直接讲实例
3.1 实例讲解
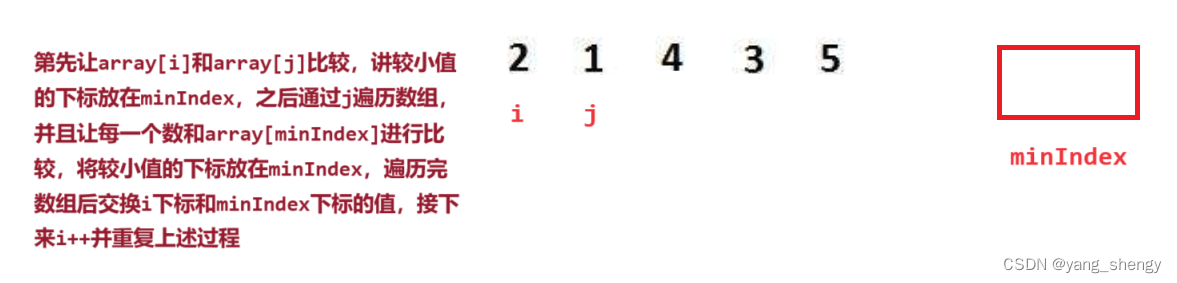
第一躺:

第二趟:

第三趟:

第四躺和第五躺也都是如此排序的,由于数据已经有序,这里就不再演示
3.2 代码实现
public void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;int j = i + 1;for (; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, minIndex, i);}}private void swap(int[] array, int minIndex, int i) {int tmp = array[minIndex];array[minIndex] = array[i];array[i] = array[minIndex];}
选择排序的效率不是很高,日常开发使用较少
时间复杂度:O(N²)
空间复杂度:O(1)
不稳定
四、堆排序
在上篇文章:Java优先级队列(堆)中进行了讲解,这里只给出代码:
4.1 代码实现
public void createHeap(int[] array) { //创建大根堆int usedSize = array.length;for (int parent = (usedSize - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array, parent, usedSize);}}private void siftDown(int[] array, int parent, int end) { //向下调整int child = 2 * parent + 1;while(child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[parent] < array[child]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}private void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public void heapSort(int[] array) { //堆排序createHeap(array);int end = array.length - 1;while(end > 0) {swap(array, 0, end);siftDown(array, 0, end - 1);end--;}}堆排序:
时间复杂度:O(N * logN)
空间复杂度:O(1)
不稳定
五、冒泡排序
冒泡排序在C语言阶段也进行了详细讲解,这里也只给出代码:
5.1 代码实现
public void bubbleSort(int[] array) {for (int i = array.length - 1; i > 0; i--) {for (int j = 0; j < i; j++) {if (array[j] > array[j + 1]) {int tmp = array[j];array[j] = array[j + 1];array[j + 1] = tmp;}}}}
冒泡排序
时间复杂度:O(N²)
空间复杂度:O(1)
稳定
六、快速排序
6.1 实例讲解
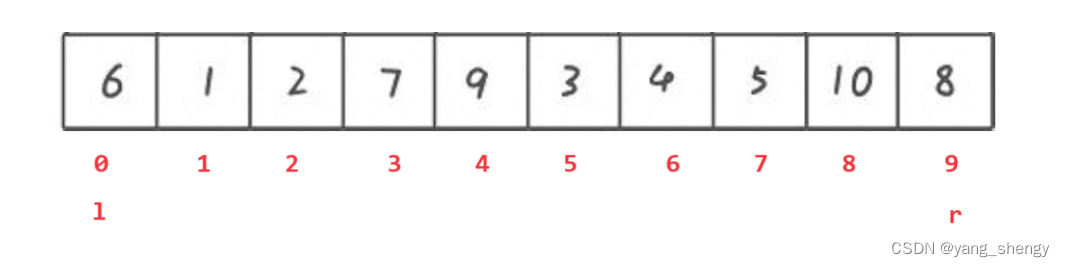
以最左边的数作为基准,先从数组的最右边开始遍历,当找到比基准小的数时停止,然后从数组的最左边开始遍历,当找到比基准大的数时停止,这时将 l 和 r 所对应的值进行交换,之后重复上述过程直到 left 和 right 相遇,相遇的下标定义为pivot,最后将pivot下标的值和tmp进行交换
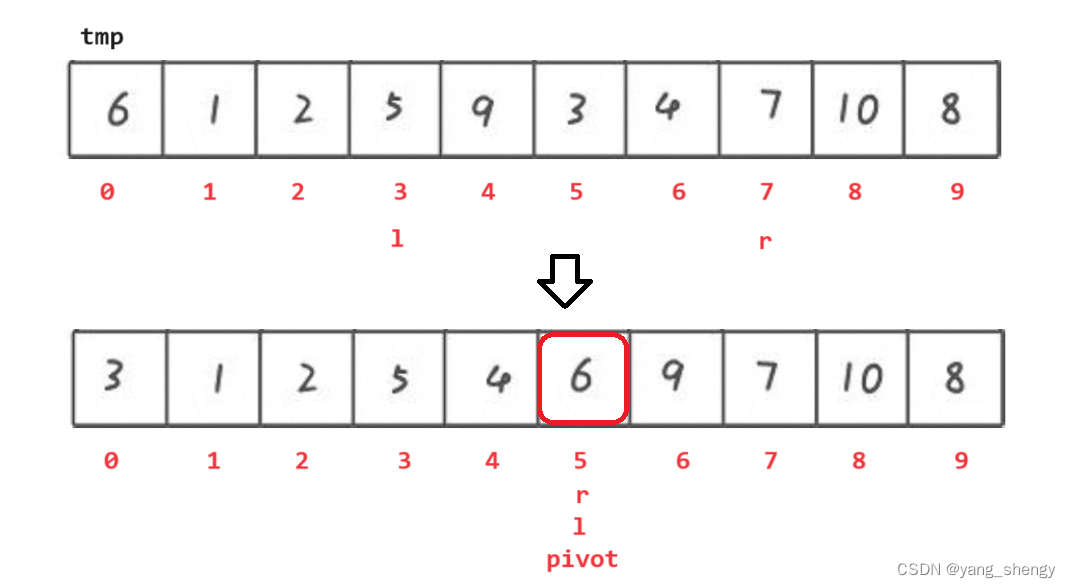
此时6的左边都是比其小的数,6的右边都是比其大的数;之后分别对6左边的数据和右边的数据进行重复的操作
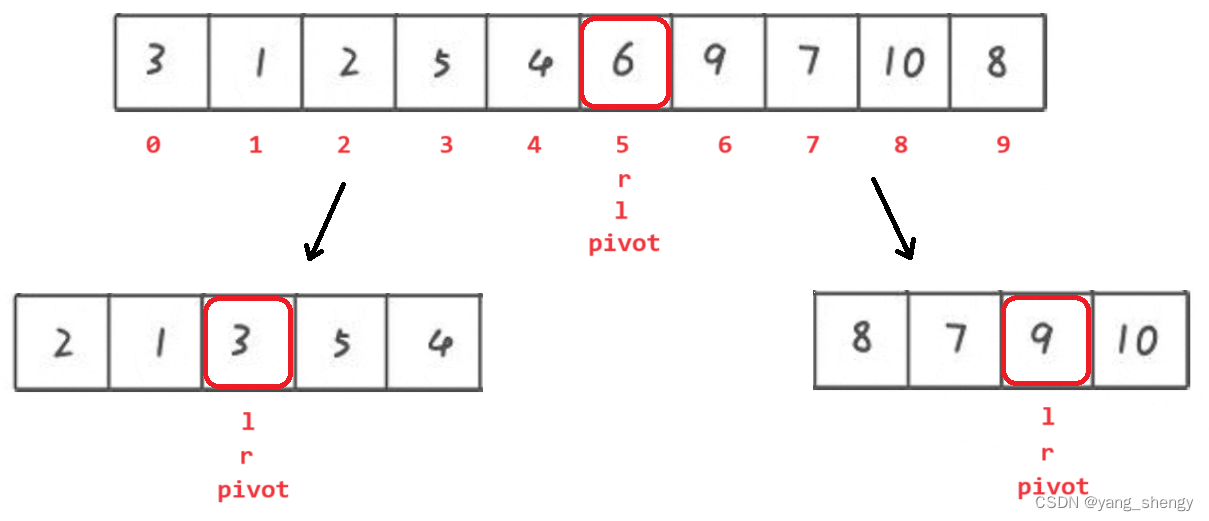
之后再对这两组数据的pivot的两边进行重复操作,由此可以联想到使用递归,类似于二叉树
6.2 代码实现
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {int pivot = partition(array, start, end); //通过paratition方法得到 left 和 right 相遇的下标 (paratition后续再实现)quick(array, start, pivot - 1); //递归 pivot 的左边quick(array, pivot + 1, end); //递归 pivot 的右边}上述的 quick 方法中还缺少递归结束的条件,第一种不难想到就是left 和 right相遇时
第二种情况如下图:
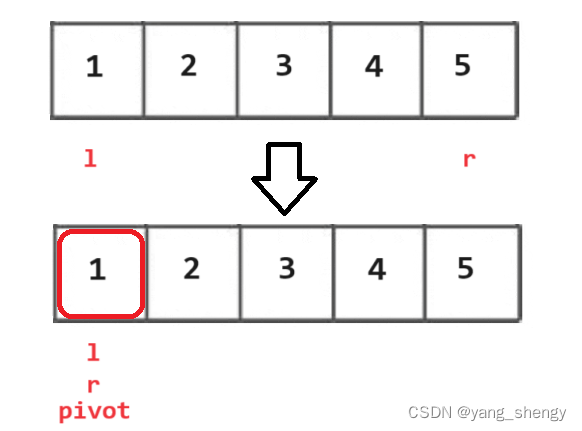
上图的下一步是r = pivot - 1;开始递归pivot的左边,但其左边并没有数据,所以当left > right时结束递归
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}private void quick(int[] array, int start, int end) {if (start >= end) {return;}int pivot = partition1(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}private int partition(int[] array, int left, int right) { //确定pivotint tmp = array[left]; //基准int i = left;while(left < right) {while(left < right && array[right] >= tmp) {right--;}while(left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, i, right);return left;}上述的 partition 确定pivot的下标被称为Hoare法,接下来再介绍一种 “挖坑法”

仍然是先从右边开始遍历,找到比tmp小的数则放在空出来的位置,此时right下标的位置就空出来了,然后从左边开始遍历找到比tmp大的数则放在空出来的位置,重复上述过程
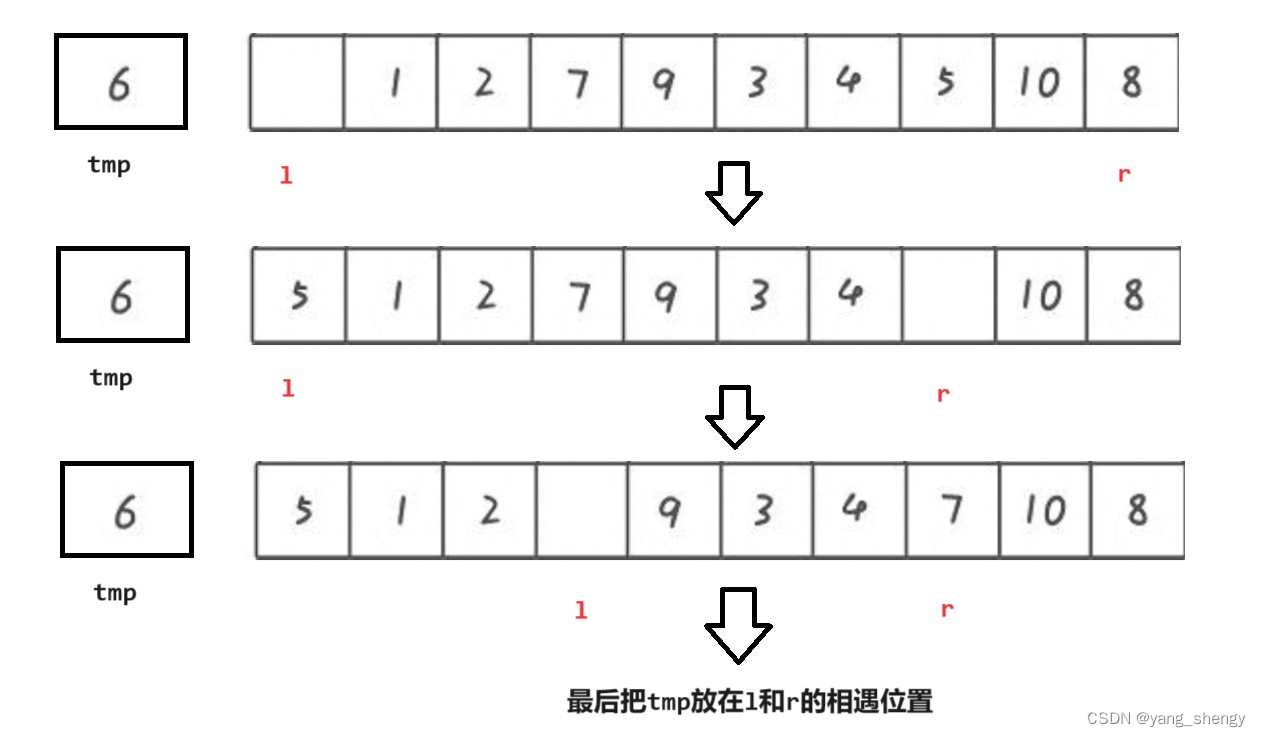
// 挖坑法private int partition(int[] array, int left, int right) {int tmp = array[left];while(left < right) {while(left < right && array[right] >= tmp) {right--;}array[left] = array[right];while(left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}
6.3 快速排序的优化
一组数据在较为理想的情况下,每次找到的基准元素都可以将这组数据分为大致相等的两部分,此时的快速排序算法的时间复杂度为 O(nlogn) ,但是也会存在一些极端的情况:每次找到的基准元素都是这组数据的最大值或最小值,此时会出现"单分支"的情况,时间复杂度为O(n^2)

6.3.1 三数取中法
改优化方法主要针对趋于有序的待排数组(升序或逆序),比如有这样一组数据:1,2,3,4,5在每一次取基准元素之前,分别取该数组的第一个数,最后一个数和中间的数,取这三个数的中间大的数和第一个数进行交换,交换完后上述数组就会变成:3,2,1,4,5,这样就是上述提到的较为理想的情况
private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果待排数组趋于有序,则采用三数取中法进行优化int index = middleNum(array, start, end);swap (array, start, index);int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}
6.3.2 递归到小的子区间时,进行直接插入排序
之前有说道:待排数据的有序性越强,直接插入排序的效率越高,所以可以考虑当快排的递归深度较深或者说递归到的子区间较小时,采用直接插入排序,这样也可以提升快速排序的效率
private static void quick(int[] array, int start, int end) {if (start >= end) {return;}//如果区间较小,则使用这种优化if (end - start + 1 <= 10) {insertSort(array, start, end);return;}int pivot = partition(array, start, end);quick (array, start, pivot - 1);quick (array, pivot + 1, end);}public static void insertSort(int[] array, int start, int end) { //这里不能只传数组,因为并不是对整个数组进行插入排序,而是某一个子区间进行直接插入排序for (int i = start + 1; i <= end; i++) { //由于只是对特定的区间进行插入排序,所以这里要限定空间int tmp = array[i];int j = i - 1;for (; j >= start; j--) { // >=startif (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
快速排序时间复杂度:最好:O(N*logN),最坏:O(N²),平均:O(N*logN)
空间复杂度:O(logN)
不稳定
七、归并排序
7.1 实例讲解
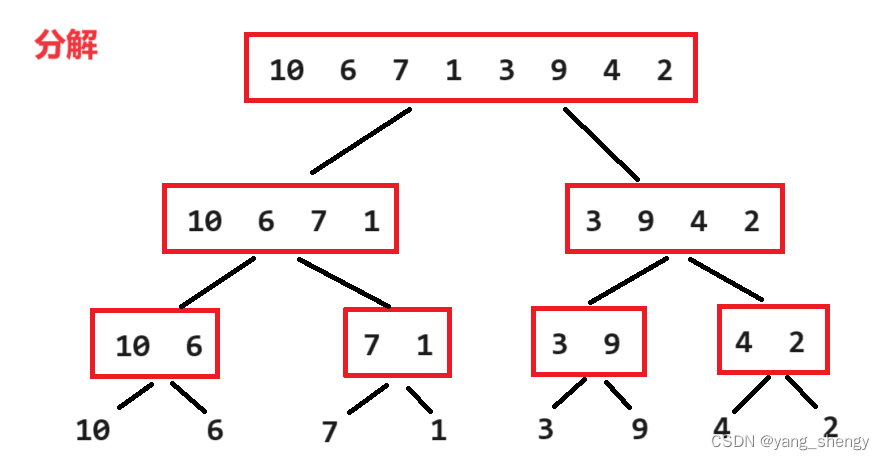
归并排序是先将待排数组递归的进行两两分组,直到每组只有一个元素,之后两两递归的进行有序合并
7.2 代码实现
先进行分解
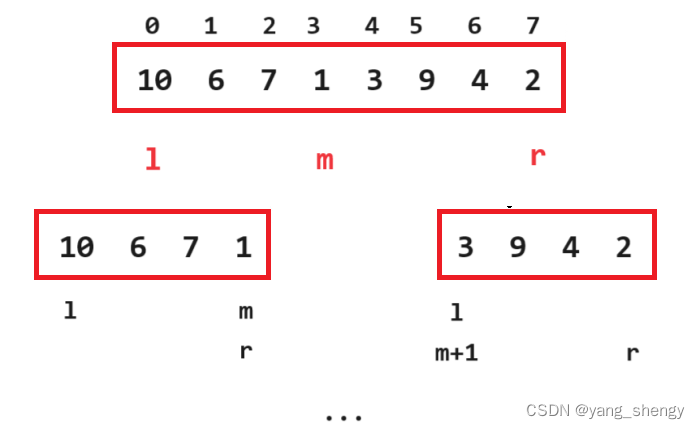
public static void mergeSort (int[] array) {//将待排数组进行分解mergeFunc(array, 0, array.length - 1);}private static void mergeFunc (int[] array, int left, int right) {if (left >= right) {return;}int mid = left + ((right - left) >> 1); //得到改组数据的中间下标//分别分解数组的左边和右边mergeFunc (array, left, mid);mergeFunc (array, mid + 1, right);//将分解后的数组进行 二路归并merge (array, left, mid, right);}
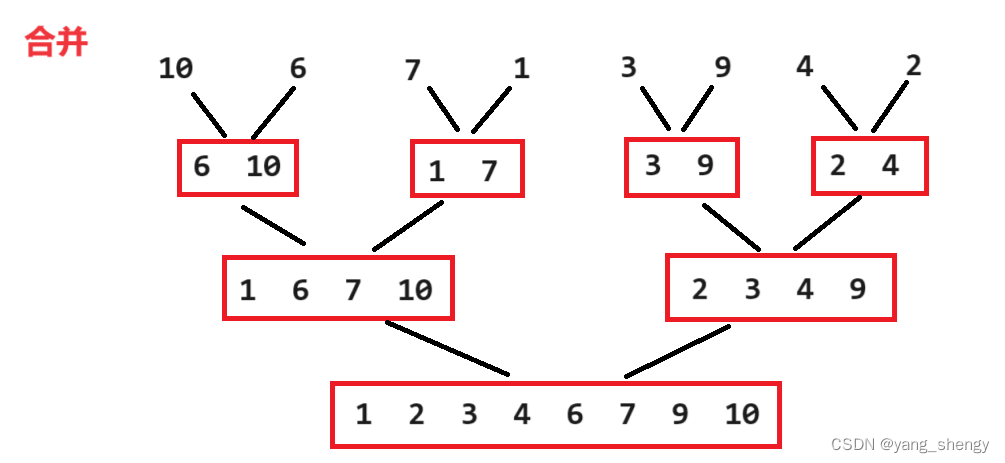
之后进行合并,以下面这一组为例:

将上面这两组数据进行有序合并,可以给这两组数据的第一个元素和最后一个元素的下标分别定义为s1,e1,s2,e2;之后再创建一个数组tmpArr,每次比较s1和s2的值,并将较小的值放在tmpArr中,(如果s1的值较小则s1++,反之s2++),然后将tmpArr中的数据再拷贝到原数组中
private static void merge (int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int[] tmpArr = new int[right - left + 1];int k = 0;//1.保证两个表都有数据while (s1 <= e1 && s2 <= e2) {if (array[s1] < array[s2]) {tmpArr[k++] = array[s1++];} else {tmpArr[k++] = array[s2++];}}//2.上个循环走完之后,可能还有一个表的数据没有全部放到tmpArr中while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}//3.将tmpArr中的数据拷贝回原数组中for (int i = 0; i < k; i++) {array[i + left] = tmpArr[i]; //array[i + left]是因为合并的两组数据不一定是原数组的0下标开始}}
时间复杂度:O(N*logN)
空间复杂度:O(N)
不稳定
🙉本篇文章到此结束
相关文章:

Java 7大排序
🐵本篇文章将对数据结构中7大排序的知识进行讲解 一、插入排序 有一组待排序的数据array,以升序为例,从第二个数据开始(用tmp表示)依次遍历整组数据,每遍历到一个数据都再从tmp的前一个数据开始࿰…...

vue3 - 图灵
目录 vue3简介整体上认识vue3项目创建Vue3工程使用官方脚手架创建Vue工程[推荐] 主要⼯程结构 数据双向绑定vue2语法的双向绑定简单表单双向绑定复杂表单双向绑定 CompositionAPI替代OptionsAPICompositionAPI简单不带双向绑定写法CompositionAPI简单带双向绑定写法setup简写⽅…...

java设计模式八 享元
享元模式(Flyweight Pattern)是一种结构型设计模式,它通过共享技术有效地支持大量细粒度的对象。这种模式通过存储对象的外部状态在外部,而将不经常变化的内部状态(称为享元)存储在内部,以此来减…...

ELK原理详解
ELK原理详解 一、引言 在当今日益增长的数据量和复杂的系统环境中,日志数据的收集、存储、分析和可视化成为了企业运营和决策不可或缺的一部分。ELK(Elasticsearch、Logstash、Kibana)堆栈凭借其高效的性能、灵活的扩展性和强大的功能&…...
多线程学习Day09
10.Tomcat线程池 LimitLatch 用来限流,可以控制最大连接个数,类似 J.U.C 中的 Semaphore 后面再讲 Acceptor 只负责【接收新的 socket 连接】 Poller 只负责监听 socket channel 是否有【可读的 I/O 事件】 一旦可读,封装一个任务对象&#x…...

第33次CSP认证Q1:词频统计
🍄题目描述 在学习了文本处理后,小 P 对英语书中的 𝑛n 篇文章进行了初步整理。 具体来说,小 P 将所有的英文单词都转化为了整数编号。假设这 𝑛n 篇文章中共出现了 𝑚m 个不同的单词,则把它们…...
pytorch加载模型出现错误
大概的错误长下面这样: 问题出现的原因: 很明显,我就是犯了第一种错误。 网上的修改方法: 我觉得按道理哈,确实,蓝色部分应该是可以把问题解决了的。但是我没有解决,因为我犯了另外一个错…...
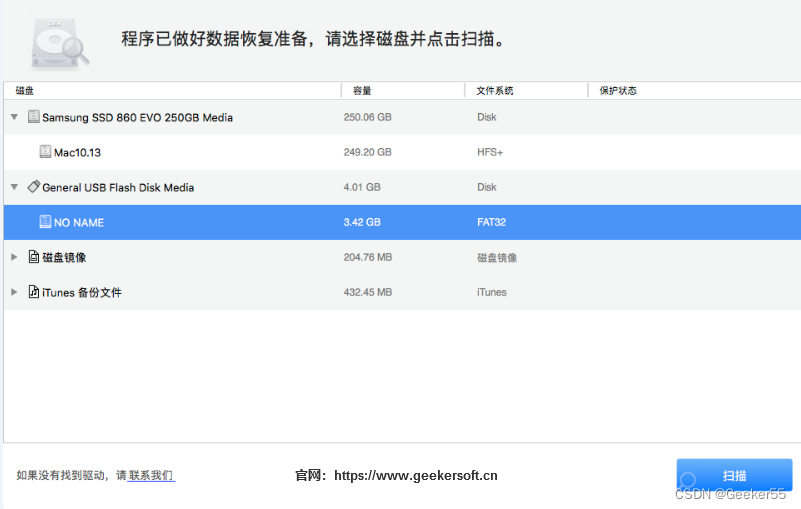
如何在Mac上恢复格式化硬盘的数据?
“嗨,我格式化了我的一个Mac硬盘,而没有使用Time Machine备份数据。这个硬盘被未知病毒感染了,所以我把它格式化为出厂设置。但是,我忘了备份我的文件。现在,我想恢复格式化的硬盘驱动器并恢复我的文档,您能…...

华为OD机试 - 手机App防沉迷系统(Java 2024 C卷 100分)
华为OD机试 2024C卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷C卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测试…...
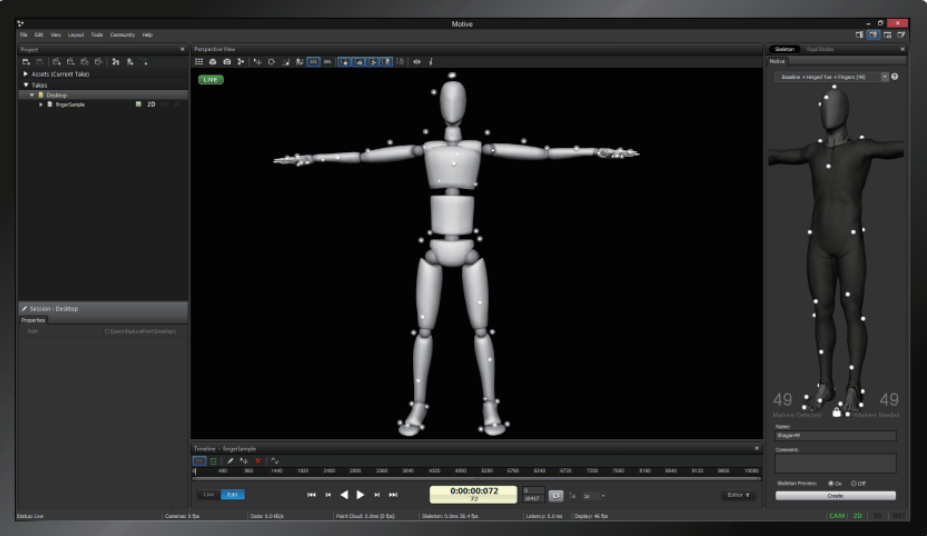
搜维尔科技:光学动作捕捉系统用于城市公共安全智慧感知实验室
用户名称:西安科技大学 主要产品:Optitrack Priime41 光学动作捕捉系统(8头) 在6米8米的空间内,通过8个Optitrack Priime41光学动作捕捉镜头,对人体动作进行捕捉,得到用户想要的人体三维空间坐…...
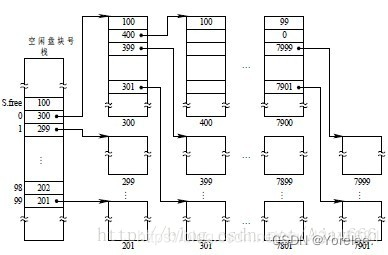
保研面试408复习 4——操作系统、计网
文章目录 1、操作系统一、文件系统中文件是如何组织的?二、文件的整体概述三、UNIX外存空闲空间管理 2、计算机网络一、CSMA/CD 协议(数据链路层协议)二、以太网MAC帧MTU 标记文字记忆,加粗文字注意,普通文字理解。 1、…...

实战攻防中关于文档的妙用
一、PPT钓鱼 简单制作一个用于钓鱼的PPTX文件 一般那种小白不知道PPT也能拿来钓鱼,这里主要是借用PPT中的”动作按钮”, 我们在插入的地方,选择“动作按钮” 然后在弹出的窗口处: 比如填入上线CS的语句:powershell.exe -nop -w …...

【使用ChatGPT的API之前】OpenAI API提供的可用模型
文章目录 一. ChatGPT基本概念二. OpenAI API提供的可用模型1. InstructGPT2. ChatGPT3. GPT-4 三. 在OpenAI Playground中使用GPT模型-ing 在使用GPT-4和ChatGPT的API集成到Python应用程序之前,我们先了解ChatGPT的基本概念,与OpenAI API提供的可用模型…...

【C语言】模拟实现深入了解:字符串函数
🔥引言 本篇将模拟实现字符串函数,通过底层了解更多相关细节 🌈个人主页:是店小二呀 🌈C语言笔记专栏:C语言笔记 🌈C笔记专栏: C笔记 🌈喜欢的诗句:无人扶我青云志 我自…...

钩子函数onMounted定义了太多访问MySQL的操作 导致数据库异常
先放几种后端遇到的异常,多数和数据库有关 pymysql.err.InternalError: Packet sequence number wrong - got 102 expected 1 127.0.0.1 - - [09/May/2024 17:49:37] "GET /monitorLastTenList HTTP/1.1" 500 AttributeError: NoneType object has no at…...
Excel文件解析---超大Excel文件读写
1.使用POI写入 当我们想在Excel文件中写入100w条数据时,使用XSSFWorkbook进行写入时会发现,只有将100w条数据全部加载到内存后才会用write()方法统一写入,效率很低,所以我们引入了SXXFWorkbook进行超大Excel文件读写。 通过设置 …...

TypeScript基础:类型系统介绍
TypeScript基础:类型系统介绍 引言 TypeScript,作为JavaScript的一个超集,引入了类型系统,这为开发大型应用程序带来了诸多好处。本文将介绍TypeScript类型系统的基础知识,帮助初学者理解其概念和用法。 基础知识 …...
【Unity】Unity项目转抖音小游戏(一) 项目转换
UnityWEBGL转抖音小游戏流程 业务需求,开始接触一下抖音小游戏相关的内容,开发过程中记录一下流程。 相关参考: 抖音文档:https://developer.open-douyin.com/docs/resource/zh-CN/mini-game/develop/guide/game-engine/rd-to-SC…...

element-ui 中修改loading加载样式
element-ui 中的 loading 加载功能,默认是全屏加载效果 设置局部,需要自定义样式或者修改样式,方法如下: import { Loading } from element-uiVue.prototype.$baseLoading (text) > {let loadingloading Loading.service({…...
)
QT登录界面,(页面的切换)
以登陆界面为例,(QDialog) 1.主界面先构造login 的对话框类 int main(int argc, char *argv[]) {QApplication a(argc, argv);//先显示Login的界面Study_Login_Dialog login;............ }2.Login的类,可以用自定义的信号&#…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...
