数据结构与算法学习笔记-二叉树的顺序存储表示法和实现(C语言)
目录
前言
1.数组和结构体相关的一些知识
1.数组
2.结构体数组
2.二叉树的顺序存储表示法和实现
1.定义
2.初始化
3.先序遍历二叉树
4.中序遍历二叉树
5.后序遍历二叉树
6.完整代码
前言
二叉树的非递归的表示和实现。
1.数组和结构体相关的一些知识
1.数组
在C语言中,可以将数组作为参数传递给函数。当数组作为参数传递时,实际上传递给函数的是数组的地址,而不是数组的副本。这意味着,在函数内部对数组进行的修改会影响到原始数组。
例如在下面的代码中,我们把数组名作为参数传递给modifyArray函数,在函数中修改数组的值,main函数打印原来的数组,会发现原来的数组也被修改。
#include <stdio.h>
#include <stdlib.h>void modifyArray(int *s,int size){for (int i = 0; i < size; i++) {s[i] = s[i] * 10;}printf("\n");
}int main(int argc, const char *argv[]) {int arr[5] = {1,2,3,4,5};int length = sizeof(arr) / sizeof(arr[0]);printf("修改之前的数组:\n");for (int i = 0; i < length;i++) {printf("%d\t",arr[i]);}modifyArray(arr,length);printf("\n修改之前的数组:\n");for (int i = 0; i < length;i++) {printf("%d\t",arr[i]);}printf("\n");return 0;
}
当然上述的函数我们还可以写成数组的形式。
void modifyArray(int s[],int size){for (int i = 0; i < size; i++) {s[i] = s[i] * 10;}printf("\n");
}2.结构体数组
在上述的代码中,我们使用数组操作基本数据类型非常的方便。当时当我们需要自定义数据类型的时候,上述的代码就不满足我们的需求了。例如我们需要表示学生数组的时候,因为每个学生都有自己的属性,姓名,年龄等等,这个时候我们就需要使用结构体数组。
在数据结构中,我们有时候需要使用数组表示一些数据类型,因此有时候我们需要把数组声明为全局函数。代码实例如下:
#include <stdio.h>
#include <stdlib.h>// 学生结构体
typedef struct {char name[50]; // 姓名int age; // 年龄
} Student;int main() {// 创建一个包含3个学生对象的数组并初始化Student students[3] = {{"张三", 20},{"李四", 21},{"王五", 22}};// 输出学生信息printf("学生信息如下:\n");for (int i = 0; i < 3; i++) {printf("学生姓名:%s\n", students[i].name);printf("学生年龄:%d\n", students[i].age);}return 0;
}2.二叉树的顺序存储表示法和实现
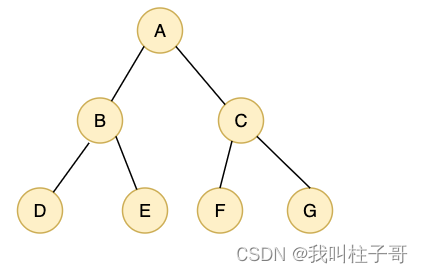
图1.完全二叉树
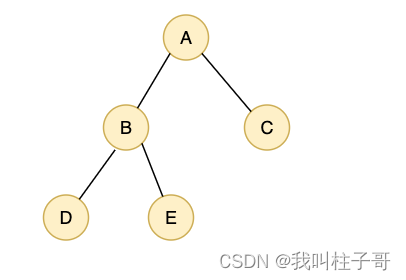
图2.普通二叉树
我们使用一组连续的存储空间表示树的结构。按照从上到下、从左到右的顺序存储完全二叉树的的节点,对于一般二叉树上的点,我们使用0表示不存在该节点。
对于图1来说,内存中的存储结构如下图3所示。

图3.完全二叉树的存储结构
如果不是二叉树,假如我们使用0表示结点不存在,图2所示的存储结构如图4所示。

图4.普通二叉树
下面我们看看如果使用代码来实现。
1.定义
我们使用数组实现二叉树的顺序存储
#define MAX_TREE_SIZE 100typedef char TElemType;
typedef int Status;typedef TElemType SqBiTree[MAX_TREE_SIZE];2.初始化
初始化时候,将数组中的元素全部设为"\0"
// 初始化二叉树
Status initSqBiTree(SqBiTree tree) {for (int i = 0; i< MAX_TREE_SIZE; i++) {tree[i] = '\0';}// 将二叉树所有元素初始化为空return 1; // 初始化成功
}3.先序遍历二叉树
遍历二叉树之前我们观察下根节点、左子树节点、右子树节点的规律。
根节点的下标为a[0].左子树上的节点的下标依次为1,3,...2*i+1,右子树上的节点的下标依次为2,4,...2*i+2
// 前序遍历二叉树
void preOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 访问根节点printf("%c ", tree[node_index]);// 递归遍历左子树preOrderTraverse(tree, 2 * node_index + 1);// 递归遍历右子树preOrderTraverse(tree, 2 * node_index + 2);}
}4.中序遍历二叉树
// 中序遍历二叉树
void inOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 递归遍历左子树inOrderTraverse(tree, 2 * node_index + 1);// 访问根节点printf("%c ", tree[node_index]);// 递归遍历右子树inOrderTraverse(tree, 2 * node_index + 2);}
}5.后序遍历二叉树
// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 递归遍历左子树postOrderTraverse(tree, 2 * node_index + 1);// 递归遍历右子树postOrderTraverse(tree, 2 * node_index + 2);// 访问根节点printf("%c ", tree[node_index]);}
}6.完整代码
#include <stdio.h>#define MAX_TREE_SIZE 100typedef char TElemType;
typedef int Status;typedef TElemType SqBiTree[MAX_TREE_SIZE];// 初始化二叉树
Status initSqBiTree(SqBiTree tree) {for (int i = 0; i< MAX_TREE_SIZE; i++) {tree[i] = '\0';}// 将二叉树所有元素初始化为空return 1; // 初始化成功
}// 前序遍历二叉树
void preOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 访问根节点printf("%c ", tree[node_index]);// 递归遍历左子树preOrderTraverse(tree, 2 * node_index + 1);// 递归遍历右子树preOrderTraverse(tree, 2 * node_index + 2);}
}// 中序遍历二叉树
void inOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 递归遍历左子树inOrderTraverse(tree, 2 * node_index + 1);// 访问根节点printf("%c ", tree[node_index]);// 递归遍历右子树inOrderTraverse(tree, 2 * node_index + 2);}
}// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 递归遍历左子树postOrderTraverse(tree, 2 * node_index + 1);// 递归遍历右子树postOrderTraverse(tree, 2 * node_index + 2);// 访问根节点printf("%c ", tree[node_index]);}
}int main(int argc, const char *argv[]) {SqBiTree tree;// 初始化二叉树initSqBiTree(tree);// 构造一个简单的二叉树,根节点为'A',左子树为'B',右子树为'C'tree[0] = 'A';tree[1] = 'B';tree[2] = 'C';tree[3] = 'D';tree[4] = 'E';tree[5] = '\0';tree[6] = '\0';// 输出初始化后的二叉树printf("前序遍历结果为:");preOrderTraverse(tree, 0);printf("\n");printf("中序遍历结果为:");inOrderTraverse(tree, 0);printf("\n");printf("后序遍历结果为:");postOrderTraverse(tree, 0);printf("\n");return 0;
}// 后序遍历二叉树
void postOrderTraverse(SqBiTree tree, int node_index) {if (node_index < MAX_TREE_SIZE && tree[node_index] != '\0') {// 递归遍历左子树postOrderTraverse(tree, 2 * node_index + 1);// 递归遍历右子树postOrderTraverse(tree, 2 * node_index + 2);// 访问根节点printf("%c ", tree[node_index]);}
}int main(int argc, const char *argv[]) {SqBiTree tree;// 初始化二叉树initSqBiTree(tree);// 构造一个简单的二叉树,根节点为'A',左子树为'B',右子树为'C'tree[0] = 'A';tree[1] = 'B';tree[2] = 'C';tree[3] = 'D';tree[4] = 'E';tree[5] = '\0';tree[6] = '\0';// 输出初始化后的二叉树printf("前序遍历结果为:");preOrderTraverse(tree, 0);printf("\n");printf("中序遍历结果为:");inOrderTraverse(tree, 0);printf("\n");printf("后序遍历结果为:");postOrderTraverse(tree, 0);printf("\n");return 0;
}
在main函数中,我们构建了一个图2所示的二叉树,控制台打印信息如下:

相关文章:

数据结构与算法学习笔记-二叉树的顺序存储表示法和实现(C语言)
目录 前言 1.数组和结构体相关的一些知识 1.数组 2.结构体数组 2.二叉树的顺序存储表示法和实现 1.定义 2.初始化 3.先序遍历二叉树 4.中序遍历二叉树 5.后序遍历二叉树 6.完整代码 前言 二叉树的非递归的表示和实现。 1.数组和结构体相关的一些知识 1.数组 在C语…...

如何在Windows和Linux中杀死Python进程
在开发和运行Python脚本的过程中,有时我们需要强制结束正在运行的Python进程。这可能是因为脚本运行出现了不可预见的错误,或者我们需要停止一个长时间执行的任务。无论原因如何,了解如何在不同操作系统中正确、安全地终止Python进程都是一项…...

零基础怎么快速进行单细胞分析?
近一段时间正在努力学习单细胞相关的理论知识,发现单细胞测序和普通的真核细胞的转录组非常相似。两者之间的最大的区别在于,一个测的是单个细胞的表达,一个测的是一堆细胞的表达之和。所以从这里就可以理解,为什么网上很多教程都…...
--1965. 丢失信息的雇员)
力扣数据库题库学习(5.10日)--1965. 丢失信息的雇员
1965. 丢失信息的雇员 问题链接🐷 思路分析 先看问题的描述 编写解决方案,找到所有 丢失信息 的雇员 id。当满足下面一个条件时,就被认为是雇员的信息丢失:雇员的 姓名 丢失了,或者雇员的 薪水信息 丢失了返回这些…...
漫威争锋Marvel Rivals怎么搜索 锁区怎么搜 游戏搜不到怎么办
即将问世的《漫威争锋》(Marvel Rivals)作为一款万众期待的PvP射击游戏新星,荣耀携手漫威官方网站共同推出。定档5月11日清晨9时,封闭Alpha测试阶段将正式揭开序幕,持续时间长达十天之久。在此首轮测试窗口,…...
SpringBoot实现统一返回值+全局异常处理
在这里首先感谢的就是程序员老罗,从他的项目里面学到了这些东西。 首先就是去创建一个SpringBoot项目,这里我就不多做赘述了 封装一个统一返回对象 package com.example.demo.vo;public class ResponseVO<T> {private String status;private In…...
windows连接CentOS数据库或Tomcat报错,IP通的,端口正常监听
错误信息 数据库错误: ERROR 2003 (HY000): Cant connect to MySQL server on x.x.x.x (10060) Tomcat访问错误: 响应时间过长 ERR_CONNECTION_TIMED_OUT 基础排查工作 【以下以3306端口为例,对于8080端口来说操作是一样的,只需…...
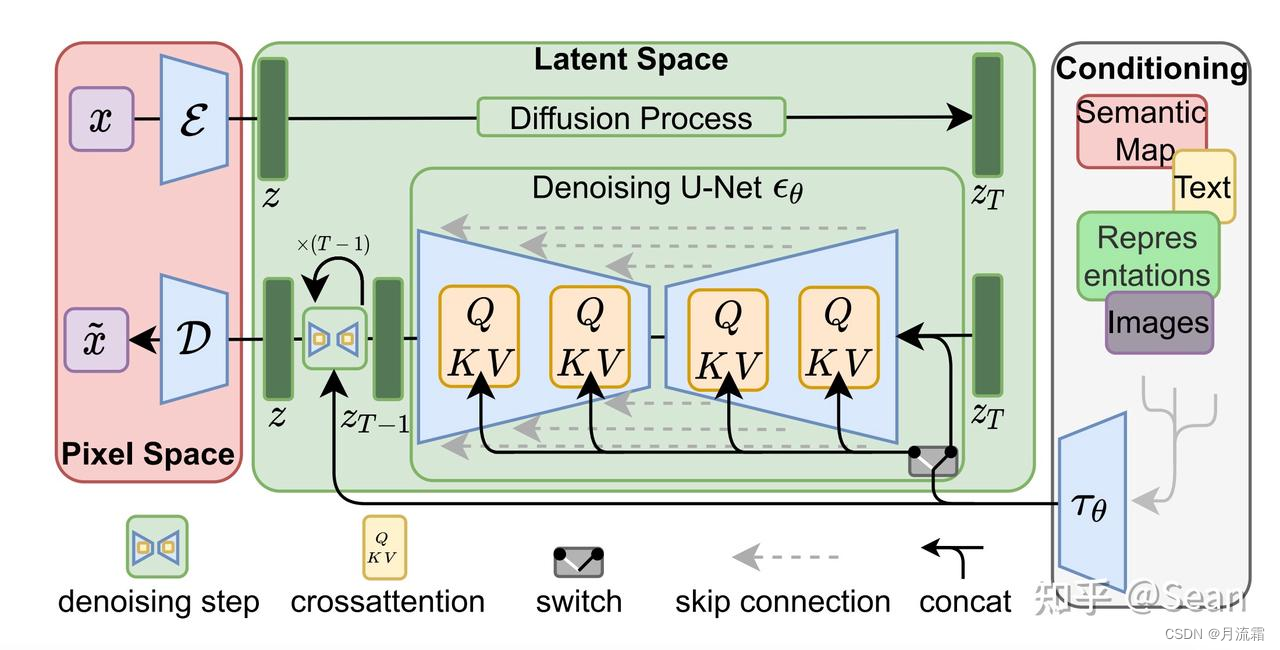
超详细的胎教级Stable Diffusion使用教程(一)
这套课程分为五节课,会系统性的介绍sd的全部功能和实操案例,让你打下坚实牢靠的基础 一、为什么要学Stable Diffusion,它究竟有多强大? 二、三分钟教你装好Stable Diffusion 三、小白快速上手Stable Diffusion 四、Stable dif…...
—— mediasoup 之媒体流score评分计算(一))
流媒体服务器(20)—— mediasoup 之媒体流score评分计算(一)
目录 前言 正文 《流媒体服务器》专栏总览丨蓄力计划_开源流媒体服务器对比-CSDN博客 前言 mediasoup 有一套评估媒体传输通道优劣的机制,主要是通过 score 评分来判断的。今天就先介绍一下这个机制的大体逻辑,后面的文章再详细介绍具体计算的算法。 正文 mediasoup 的…...

用keras识别狗狗
一、需求场景 从照片从识别出狗狗 from keras.applications.resnet50 import ResNet50 from keras.preprocessing import image from keras.applications.resnet50 import preprocess_input, decode_predictions import numpy as np# 加载预训练的ResNet50模型 model ResNet5…...
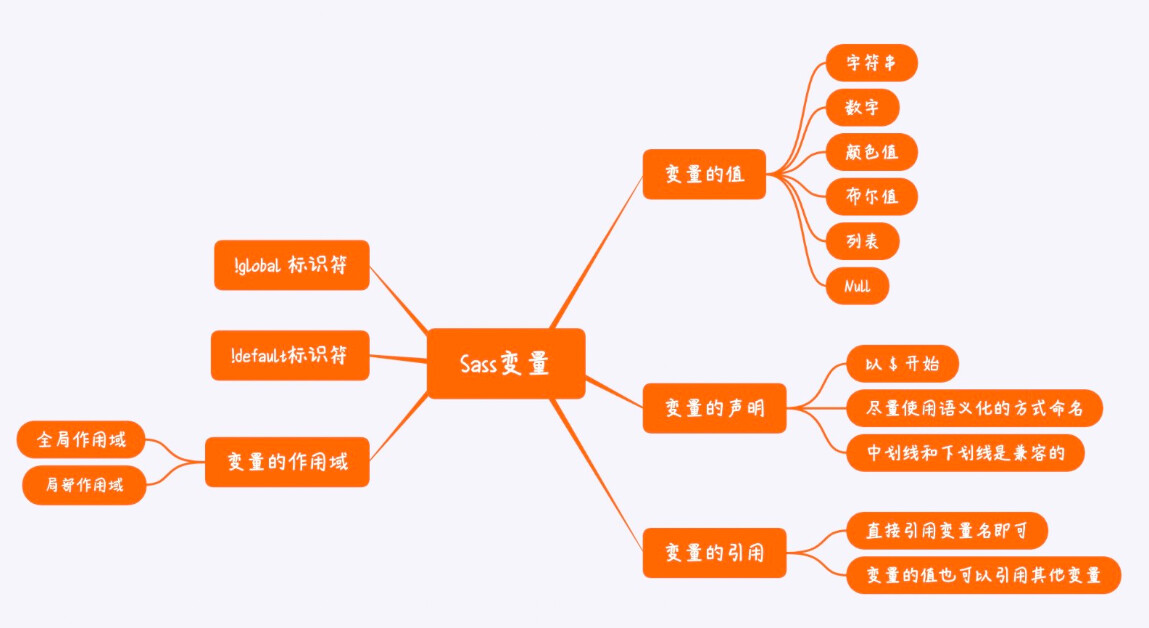
Sass语法介绍-变量介绍
02 【Sass语法介绍-变量】 sass有两种语法格式Sass(早期的缩进格式:Indented Sass)和SCSS(Sassy CSS) 目前最常用的是SCSS,任何css文件将后缀改为scss,都可以直接使用Sassy CSS语法编写。 所有有效的 CSS 也同样都是有效的 SCSS。 Sass语…...

可调恒流电子负载的基础认识
可调恒流电子负载是模拟真实负载的电子设备,它可以模拟各种不同类型和功率的负载。这种设备的主要功能是接收电源输入,然后以恒定的电流输出,以便对电源或电池进行测试和校准。 首先,我们需要了解什么是恒流,恒流是指在…...
)
开源模型应用落地-模型记忆增强-概念篇(一)
一、前言 语言模型的记忆是基于其训练数据。具体而言,对于较长的文本,模型可能会遗忘较早的信息,因为它的记忆是有限的,并且更容易受到最近出现的内容的影响。模型无法跨越其固定的上下文窗口,而是根据当前上下文生成回应。 提升模型记忆能力有多种方法,比如改进模型的结…...
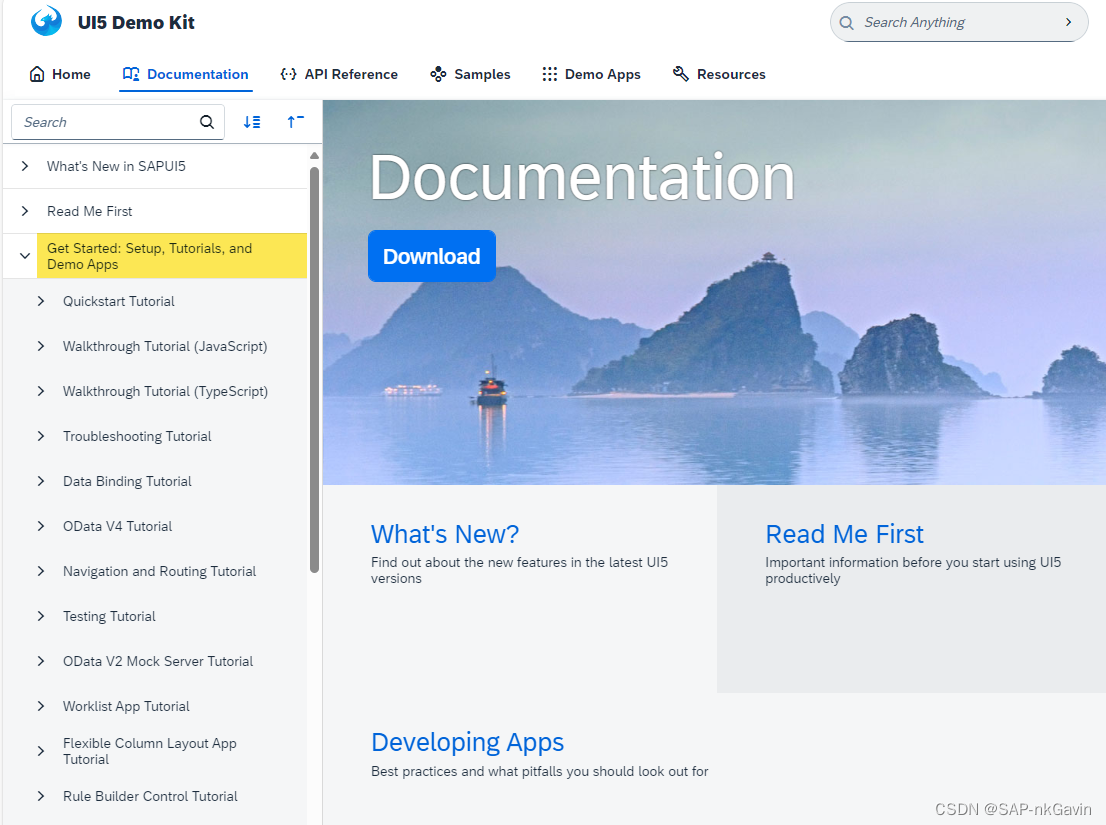
SAPUI5基础知识1 - 概览,库,支持工具,自学教程
1. SAPUI5 概览 1.1 SAPUI5 SAPUI5是一种用于构建企业级Web应用程序的开发框架。它是由SAP开发的,基于HTML5、CSS3和JavaScript技术。 SAPUI5提供了一套丰富的UI控件和工具,使开发人员能够快速构建现代化、可扩展和可定制的应用程序。 它还提供了数据…...

常见的获取dom元素的方法
获取 DOM 元素是前端开发中非常常见的操作。以下是几种常用的方法来获取 DOM 元素,以及它们的适用场景和示例: 1. getElementById 用于获取具有指定 id 属性的元素。 示例 let element document.getElementById(myId); 2. getElementsByClassName …...

走进CHEN MEI HUA的设计哲学:书写东方女性力量与态度的时尚篇章
在时尚的舞台中央,品牌不止是商品,更是故事的讲述者、文化的传承者。CHEN MEI HUA,一个源自中国上海的高端女装品牌,以其独特的设计理念及文化内核,成为了时尚界一颗耀眼的明珠。今天,让我们一起走进CMH的世…...

ESrally单机向量检索性能测试全流程
ESrally单机向量检索性能测试全流程 测试方案的尝试 准备测试 ES 的向量检索性能,Vespa 方案由于下载依赖库存在网络问题无法执行成功,终止;开源工具 ann-benchamrk 是一个用于评估近似最近邻(ANN)搜索库的性能测试工具,这个本是最佳选择,但是也由于需要 pip 安装几十…...
小红书释放被封手机号 无限注册
前几年抖音也可以释放被封手机号 那时候都不重视 导致现在被封手机号想释放 基本不可能的 或者就是最少几百块 有专业的人帮你通过某些信息差释放 本教程是拆解 小红书被封手机号怎么释放,从今年开始,被封的手机号无法注销了 所以很困扰 那么本教程来…...

Docker快速启动清单
以下容器均使用 Docker version 24.0.2 版本测试使用,这里需要注意一下,高版本的Docker不支持镜像V1版本,不知道怎么操作才可以让它支持,所以推荐使用低版本 如果觉得不直观,或者觉得有点乱,可以访问以下网…...
京东手势验证码-YOLO姿态识别+Bézier curve轨迹拟合
这次给老铁们带来的是京东手势验证码的识别。 目标网站:https://plogin.m.jd.com/mreg/index 验证码如下图: 当第一眼看到这个验证码的时候,就头大了,这玩意咋识别??? 静下心来细想后的一个方案…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
