数据可视化训练第二天(对比Python与numpy中的ndarray的效率并且可视化表示)
绪论
千里之行始于足下;继续坚持
1.对比Python和numpy的性能
使用魔法指令%timeit进行对比
需求:
- 实现两个数组的加法
- 数组 A 是 0 到 N-1 数字的平方
- 数组 B 是 0 到 N-1 数字的立方
import numpy as np
def numpy_sum(text_num):"""numpy的测试函数"""arra=np.arange(text_num) ** 2arrb=np.arange(text_num) ** 3return arra+arrbdef python_sum(text_num):"""原生Python的测试函数"""ab_sum=[]a=[value**2 for value in range(0,text_num)]b=[value**3 for value in range(0,text_num)]for i in range(0,text_num):ab_sum.append(a[i]+b[i])return ab_sumtext_num=100#保存Python的测试时间
#100,1000的数组长度测试起来时间可能比较小;可视化不太方便
python_times=[]
#进行到1000000次的时间测试
while text_num <= 1000000:result= %timeit -o python_sum(text_num)text_num=text_num*10python_times.append(result.average)#保存numpy的测试时间
numpy_times=[]
text_num=100
while text_num <= 1000000:result= %timeit -o numpy_sum(text_num)numpy_times.append(result.average)text_num=text_num*10下面通过折线图进行对比
#数据可视化对比
import matplotlib.pyplot as plt
from matplotlib.ticker import ScalarFormatterx_values=[100,1000,10000,100000,1000000]
python_y_values=np.array(python_times)*1000000
numpy_y_values=np.array(numpy_times)*1000000
fig,ax=plt.subplots()
ax.plot(x_values,python_y_values,linewidth=3,label='python')
ax.plot(x_values,numpy_y_values,linewidth=3,label='numpy')
ax.set_title("Comparing Numpy's Time with Python",fontsize=14)
ax.set_xlabel('text sum',fontsize=14)
ax.set_ylabel('time/us',fontsize=14)
#设置显示所有刻度
#ax.set_xticks(x_values,minor=True)
#使x轴完全表示,使用formatter自定义格式
formatter=ScalarFormatter(useMathText=True)#使用数学格式表示
formatter.set_powerlimits((0,7))
ax.xaxis.set_major_formatter(formatter)
ax.legend()#显示label标签
plt.show(
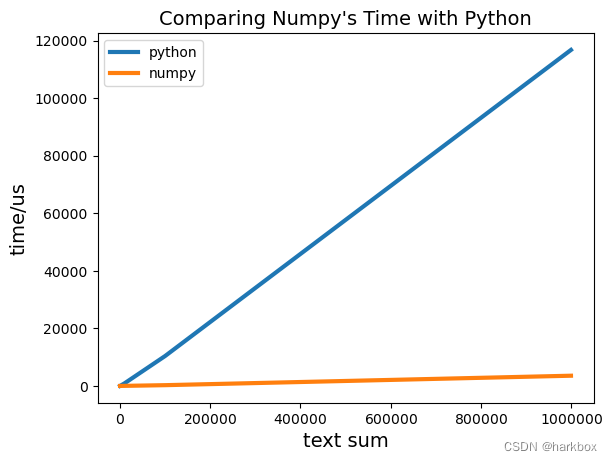
绘制柱状图
#绘制柱状图
fig,ax=plt.subplots()
bar_width=0.35
ax.bar(x_values,python_y_values,bar_width,label='Python')
ax.bar(x_values,numpy_y_values,bar_width,label='Numpy')ax.legend()#legend() 函数用于添加图例到图形上,就是右上角的图形
plt.tight_layout()
plt.show()
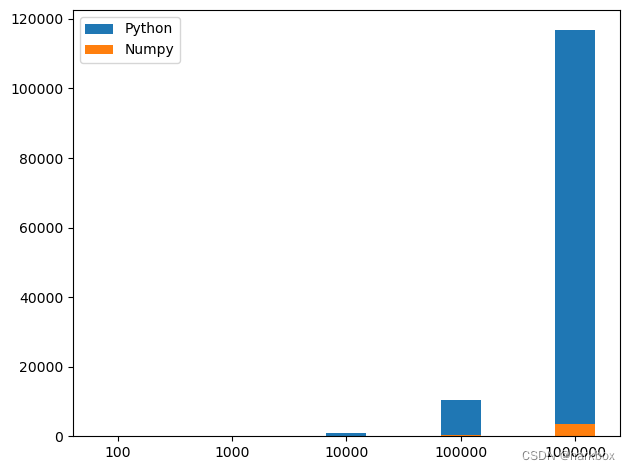
100和1000的时间太短了;可以从100000开始到100000000这样可视化会比较好看
相关文章:

数据可视化训练第二天(对比Python与numpy中的ndarray的效率并且可视化表示)
绪论 千里之行始于足下;继续坚持 1.对比Python和numpy的性能 使用魔法指令%timeit进行对比 需求: 实现两个数组的加法数组 A 是 0 到 N-1 数字的平方数组 B 是 0 到 N-1 数字的立方 import numpy as np def numpy_sum(text_num):"""…...
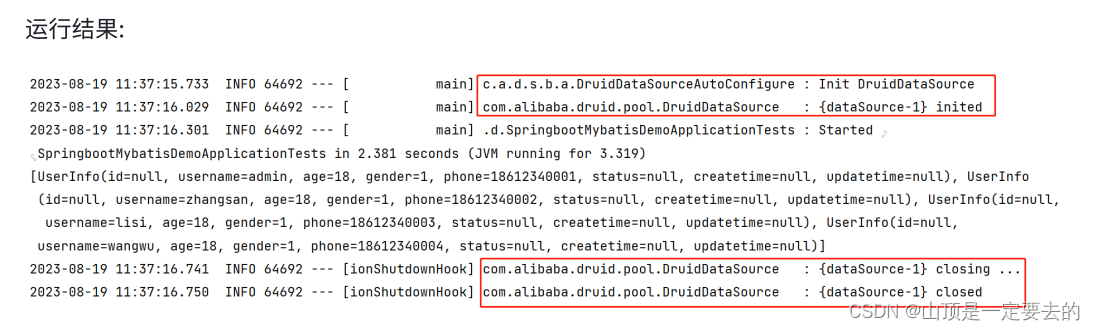
【Java EE】数据库连接池详解
文章目录 🎍数据库连接池🌸Hikari🌸Druid 🍀MySQL开发企业规范⭕总结 🎍数据库连接池 在上⾯Mybatis的讲解中,我们使⽤了数据库连接池技术,避免频繁的创建连接,销毁连接 下⾯我们来了解下数据库连接池 数据库连接池负…...

正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-15.4讲 GPIO中断实验-IRQ中断服务函数详解
前言: 本文是根据哔哩哔哩网站上“正点原子[第二期]Linux之ARM(MX6U)裸机篇”视频的学习笔记,在这里会记录下正点原子 I.MX6ULL 开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了正点原子教学视频和链接中的内容。…...

如何平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验?
平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验,是RPA实施中的一个关键挑战。以下是一些策略和最佳实践: ### 1. 安全设计原则 从设计阶段就将安全性纳入考虑,遵循安全设计原则。这意味着在开发RPA解决方案时࿰…...
地球行星UE5和UE4
地球行星,包含多种地球风格,可蓝图控制自转和停止,可材质自转. 支持版本4.21-5.4版本 下载位置:https://mbd.pub/o/bread/ZpWZm5lv b站工坊:https://gf.bilibili.com/item/detail/1105582041 _______________________…...

7.k8s中的名称空间namespace
目录 一、Namespace(命名空间) 二、查看系统的名称空间 1.查看系统中的名称空间列表 2.单独查看一个名称空间下的对应资源 三、名称空间的管理 1.创建名称空间 1.1响应式创建 1.2声明式创建 2.删除名称空间 四、资源引用名称空间 一、Namespace(命名空间) 命名空间(Name…...

上海企业源代码防泄密解决方案,企业源代码防泄密如何应对?
随之互联网的发展,企业员工因离职把企业源代码泄露或删库跑路的事情屡见不鲜,各大互联网公司基本都会出现源代码泄露的事情,这样的问题也成了企业在发展过程中不可避免的问题。企业源代码泄露会给企业带来的损失也是不可估量的,据…...

将要上市的自动驾驶新书《自动驾驶系统开发》中摘录各章片段 4
第十三章 车联网 数字化设备正变得越来越普遍并且相互联系。这些设备向数字生态系统智能部分的演进创造了迄今为止尚未解决安全问题的新颖应用。一个特定的例子是车辆,随着车辆从简单的交通方式发展到具有新的感知和通讯功能的智能实体,就成为智能城市的…...

OpenSearch 与 Elasticsearch:7 个主要差异及如何选择
OpenSearch 与 Elasticsearch:7 个主要差异及如何选择 1. 什么是 Elasticsearch? Elasticsearch 是一个基于 Apache Lucene 构建的开源、RESTful、分布式搜索和分析引擎。它旨在处理大量数据,使其成为日志和事件数据管理的流行选择。 Elasti…...

[Docker]容器的网络类型以及云计算
目录 知识梗概 1、常用命令2 2、容器的网络类型 3、云计算 4、云计算服务的几种主要模式 知识梗概 1、常用命令2 上一篇已经学了一些常用的命令,这里补充两个: 导出镜像文件:[rootdocker ~]# docker save -o nginx.tar nginx:laster 导…...
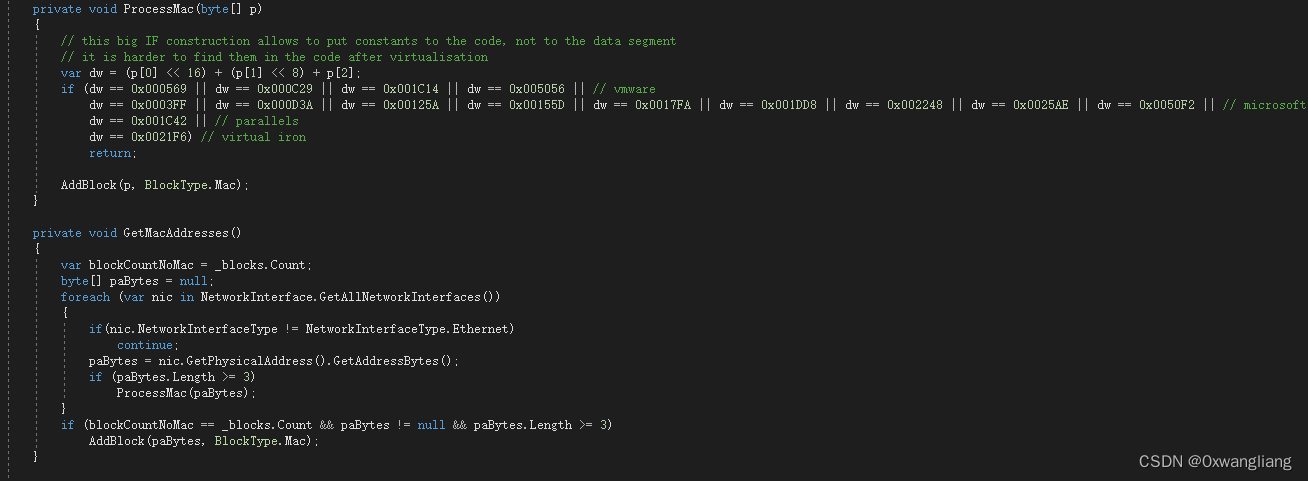
VMP 简单源码分析(.net)
虚拟机 获取CPU的型号 实现了一个指令集解释器,每个操作码对应一个特定的处理函数,用于执行相应的指令操作。在执行字节码时,解释器会根据操作码查找并调用相应的处理函数来执行指令。 截获异常 先由虚拟机处理 处理不了再抛出异常 priva…...

数据结构与算法学习笔记-二叉树的顺序存储表示法和实现(C语言)
目录 前言 1.数组和结构体相关的一些知识 1.数组 2.结构体数组 2.二叉树的顺序存储表示法和实现 1.定义 2.初始化 3.先序遍历二叉树 4.中序遍历二叉树 5.后序遍历二叉树 6.完整代码 前言 二叉树的非递归的表示和实现。 1.数组和结构体相关的一些知识 1.数组 在C语…...

如何在Windows和Linux中杀死Python进程
在开发和运行Python脚本的过程中,有时我们需要强制结束正在运行的Python进程。这可能是因为脚本运行出现了不可预见的错误,或者我们需要停止一个长时间执行的任务。无论原因如何,了解如何在不同操作系统中正确、安全地终止Python进程都是一项…...

零基础怎么快速进行单细胞分析?
近一段时间正在努力学习单细胞相关的理论知识,发现单细胞测序和普通的真核细胞的转录组非常相似。两者之间的最大的区别在于,一个测的是单个细胞的表达,一个测的是一堆细胞的表达之和。所以从这里就可以理解,为什么网上很多教程都…...
--1965. 丢失信息的雇员)
力扣数据库题库学习(5.10日)--1965. 丢失信息的雇员
1965. 丢失信息的雇员 问题链接🐷 思路分析 先看问题的描述 编写解决方案,找到所有 丢失信息 的雇员 id。当满足下面一个条件时,就被认为是雇员的信息丢失:雇员的 姓名 丢失了,或者雇员的 薪水信息 丢失了返回这些…...
漫威争锋Marvel Rivals怎么搜索 锁区怎么搜 游戏搜不到怎么办
即将问世的《漫威争锋》(Marvel Rivals)作为一款万众期待的PvP射击游戏新星,荣耀携手漫威官方网站共同推出。定档5月11日清晨9时,封闭Alpha测试阶段将正式揭开序幕,持续时间长达十天之久。在此首轮测试窗口,…...
SpringBoot实现统一返回值+全局异常处理
在这里首先感谢的就是程序员老罗,从他的项目里面学到了这些东西。 首先就是去创建一个SpringBoot项目,这里我就不多做赘述了 封装一个统一返回对象 package com.example.demo.vo;public class ResponseVO<T> {private String status;private In…...
windows连接CentOS数据库或Tomcat报错,IP通的,端口正常监听
错误信息 数据库错误: ERROR 2003 (HY000): Cant connect to MySQL server on x.x.x.x (10060) Tomcat访问错误: 响应时间过长 ERR_CONNECTION_TIMED_OUT 基础排查工作 【以下以3306端口为例,对于8080端口来说操作是一样的,只需…...
超详细的胎教级Stable Diffusion使用教程(一)
这套课程分为五节课,会系统性的介绍sd的全部功能和实操案例,让你打下坚实牢靠的基础 一、为什么要学Stable Diffusion,它究竟有多强大? 二、三分钟教你装好Stable Diffusion 三、小白快速上手Stable Diffusion 四、Stable dif…...
—— mediasoup 之媒体流score评分计算(一))
流媒体服务器(20)—— mediasoup 之媒体流score评分计算(一)
目录 前言 正文 《流媒体服务器》专栏总览丨蓄力计划_开源流媒体服务器对比-CSDN博客 前言 mediasoup 有一套评估媒体传输通道优劣的机制,主要是通过 score 评分来判断的。今天就先介绍一下这个机制的大体逻辑,后面的文章再详细介绍具体计算的算法。 正文 mediasoup 的…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...
