elementUi中的el-table合计行添加点击事件
elementUi 文档中,合计行并没有点击事件,这里自己实现了合计行的点击事件。
created() {this.propertyList = [{ property: 'order', label: '序号' },{ property: 'deptName', label: '单位名称' },{ property: 'contentPublishQuantity', label: '文章数量' },{ property: 'readQuantity', label: '浏览量' },{ property: 'likeQuantity', label: '点赞量' },{ property: 'collectionQuantity', label: '收藏量' },]},mounted() {let that = thissetTimeout(() => {const footerWrapper = this.$el.querySelector('.el-table__footer-wrapper');const cells = this.$el.querySelectorAll('.el-table__footer-wrapper td .cell');// 给文章数量和收藏量添加样式let clickIndex = [2,5]if (cells.length) {cells.forEach((cell, index) => {if (clickIndex.includes(index)) {cell.style.color = '#409EFF'cell.style.cursor = 'pointer'}})}// 在合计行添加点击事件footerWrapper.addEventListener('click', (event) => {// 检查点击事件是否发生在合计行的单元格上const targetCell = event.target.closest('.el-table__cell');if (targetCell) {// 获取点击的列索引const columnIndex = Array.from(targetCell.parentNode.children).indexOf(targetCell);if (columnIndex !== -1) {console.log('当前点击项:',that.propertyList[columnIndex])}}});}, 500)},
相关文章:

elementUi中的el-table合计行添加点击事件
elementUi 文档中,合计行并没有点击事件,这里自己实现了合计行的点击事件。 created() {this.propertyList [{ property: order, label: 序号 },{ property: deptName, label: 单位名称 },{ property: contentPublishQuantity, label: 文章数量 },{ pro…...

Zookeeper集群搭建的一些问题
问题描述一: Cannot open channel to 2 at election address /192.168.60.132:3888解决方案: 查看zookeeper配置文件zoo.cfg / zoo_sample.cfg中集群配置部分 server.1zoo1-net1:2888:3888|zoo1-net2:2889:3889 server.2zoo2-net1:2888:3888|zoo2-net2…...
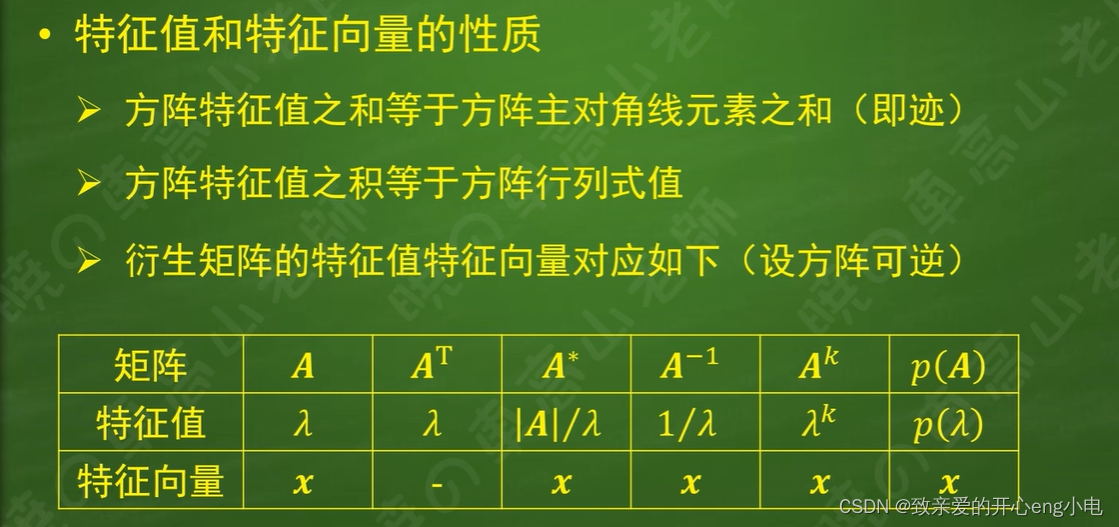
【线性代数】俗说矩阵听课笔记
基础解系的概念 线性方程组的解 21行列式和矩阵秩Rank的等价刻画 子式 标准型 利用子式求解矩阵的rank 24零积秩不等式 齐次线性方程组的基础解系 rank的两个重要结论 ¥25伴随矩阵的rank 奇异矩阵:行列式0的矩阵 31线性相关,线性无关&#…...

物联网技术在数字化工厂中的应用,你知道多少?——青创智通
工业物联网解决方案-工业IOT-青创智通 物联网(IoT)技术在数字化工厂的应用正日益成为工业革命的重要推动力。随着科技的飞速发展,物联网技术不断革新,其在数字化工厂中的应用也呈现出愈发广泛和深入的态势。本文将详细探讨物联网…...
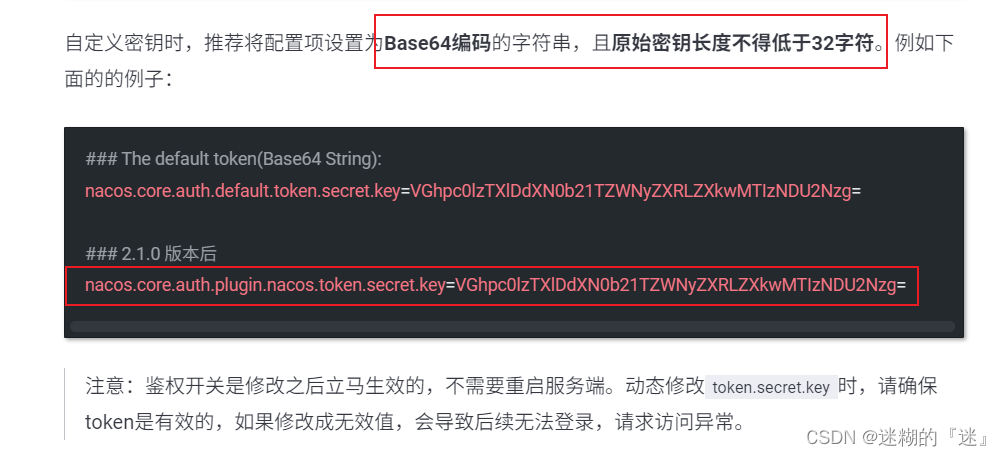
nacos开启登录开关启动报错“Unable to start embedded Tomcat”
nacos 版本:2.3.2 2.2.2版本之前的Nacos默认控制台,无论服务端是否开启鉴权,都会存在一个登录页;在之后的版本关闭了默认登录页面,无需登录直接进入控制台操作。在这里我们可以在官网可以看到相关介绍 而我现在所用的…...
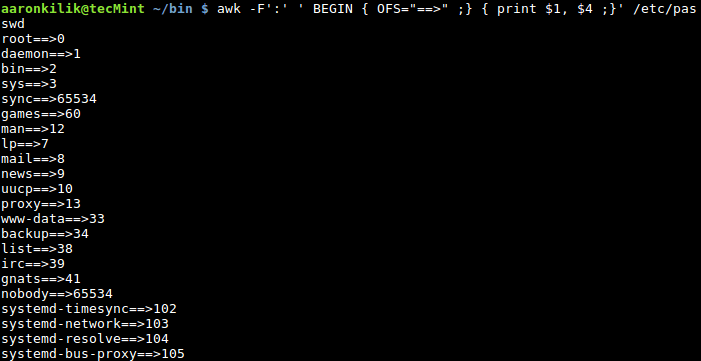
Linux|了解如何使用 awk 内置变量
引言 当我们揭开 Awk 功能部分时,我们将介绍 Awk 中内置变量的概念。您可以在 Awk 中使用两种类型的变量:用户定义的变量和内置变量。 内置变量的值已经在 Awk 中定义,但我们也可以仔细更改这些值,内置变量包括: FILEN…...

代码随想录-算法训练营day29【回溯算法05:递增子序列、全排列】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第七章 回溯算法part05* 491.递增子序列 * 46.全排列 * 47.全排列 II详细布置 491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 https://programmercarl.com…...

704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target&a…...

php回车变br、php显示br
在 PHP 中,如果你想将回车符(\n)转换为 HTML 的 <br> 标签来实现换行显示,可以使用内置函数 nl2br()。这个函数会将文本中的换行符替换为 <br> 标签。以下是使用 nl2br() 函数的示例代码: <?php $tex…...
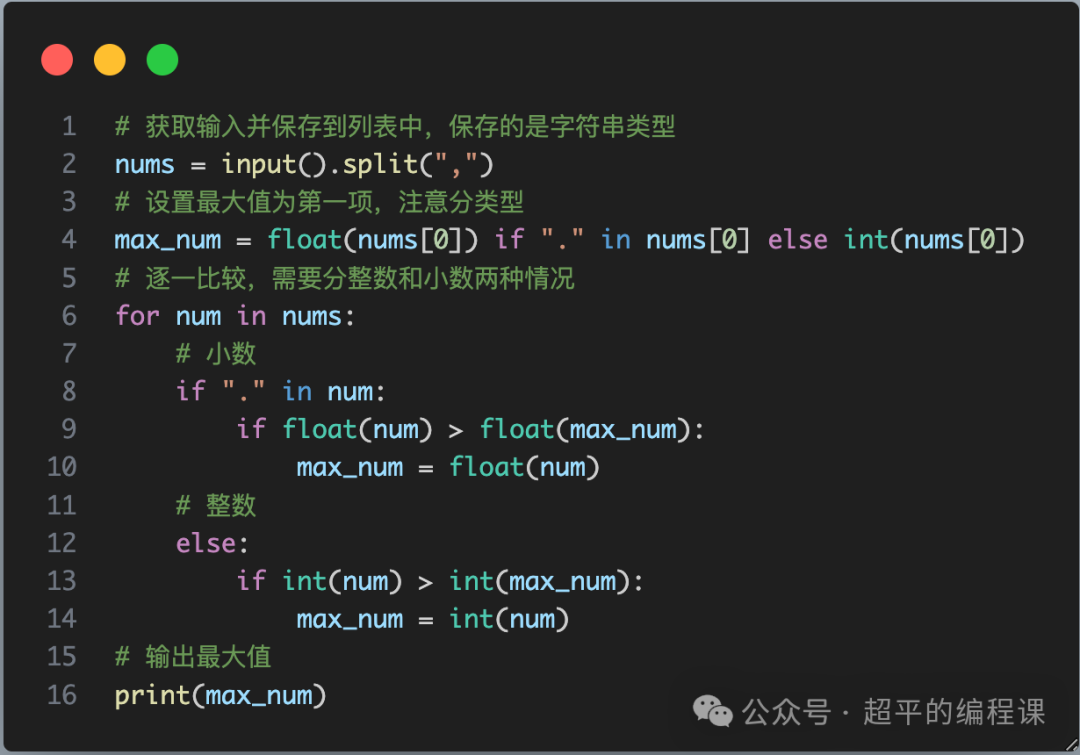
找最大数字-第12届蓝桥杯国赛Python真题解析
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第60讲。 找最大数字&#…...

蓝桥杯 算法提高 ADV-1170 阶乘测试 python AC
找规律题,遍历i中有几个m就加几,和m的多少次数有关 第一版👇 try:while True:n, m map(int, input().split())ll [i for i in range(1, n 1) if i % m 0]ans len(ll)M mwhile ll:lll []M * mfor i in ll:if i % M 0:lll.append(i)a…...

阿里巴巴杭州全球总部正式启用,创新“减碳大脑”科技减碳 | 最新快讯
来源:封面新闻 封面新闻记者付文超 5 月 10 日,记者获悉,位于未来科技城的阿里巴巴杭州全球总部新园区正式启用,这是阿里巴巴目前最大的综合性办公园区。从空中俯瞰,园区正中央呈现阿里标志性的笑脸 logo,这…...
)
蓝桥杯国赛练习题真题Java(矩阵计数)
题目描述 一个 NM 的方格矩阵,每一个方格中包含一个字符 O 或者字符 X。 要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。 问这样的矩阵一共有多少种? 输入描述 输入一行包含两个整数 N,M (1≤N,M≤5)。 输出描述 输出一个整数代表答案。…...
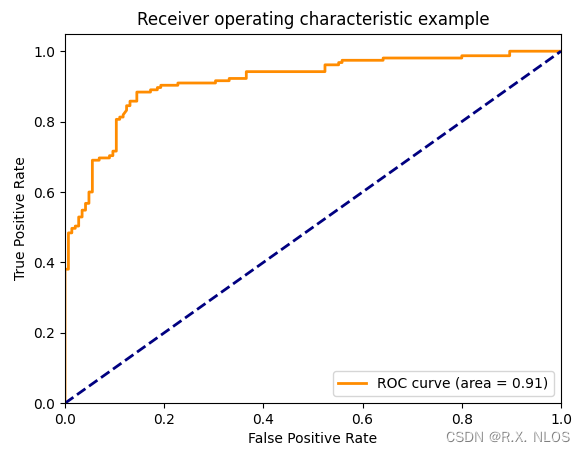
概念解析 | ROC曲线:评估分类模型
注1:本文系"概念解析"系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:ROC曲线的含义和绘制 概念解析 | ROC曲线:评估分类模型 第一部分:通俗解释 在我们的日常生活中,经常会遇到需要做出判断和选择的情况。比如,当你收到一封邮件时…...
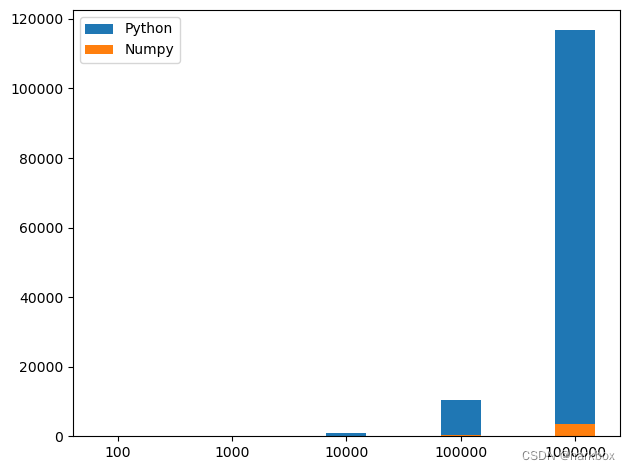
数据可视化训练第二天(对比Python与numpy中的ndarray的效率并且可视化表示)
绪论 千里之行始于足下;继续坚持 1.对比Python和numpy的性能 使用魔法指令%timeit进行对比 需求: 实现两个数组的加法数组 A 是 0 到 N-1 数字的平方数组 B 是 0 到 N-1 数字的立方 import numpy as np def numpy_sum(text_num):"""…...
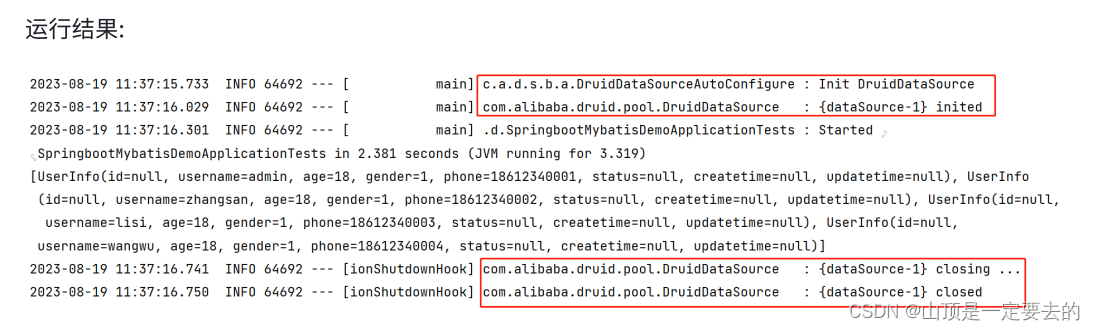
【Java EE】数据库连接池详解
文章目录 🎍数据库连接池🌸Hikari🌸Druid 🍀MySQL开发企业规范⭕总结 🎍数据库连接池 在上⾯Mybatis的讲解中,我们使⽤了数据库连接池技术,避免频繁的创建连接,销毁连接 下⾯我们来了解下数据库连接池 数据库连接池负…...

正点原子[第二期]Linux之ARM(MX6U)裸机篇学习笔记-15.4讲 GPIO中断实验-IRQ中断服务函数详解
前言: 本文是根据哔哩哔哩网站上“正点原子[第二期]Linux之ARM(MX6U)裸机篇”视频的学习笔记,在这里会记录下正点原子 I.MX6ULL 开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了正点原子教学视频和链接中的内容。…...

如何平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验?
平衡RPA机器人的安全性与业务敏捷性,同时不牺牲用户体验,是RPA实施中的一个关键挑战。以下是一些策略和最佳实践: ### 1. 安全设计原则 从设计阶段就将安全性纳入考虑,遵循安全设计原则。这意味着在开发RPA解决方案时࿰…...
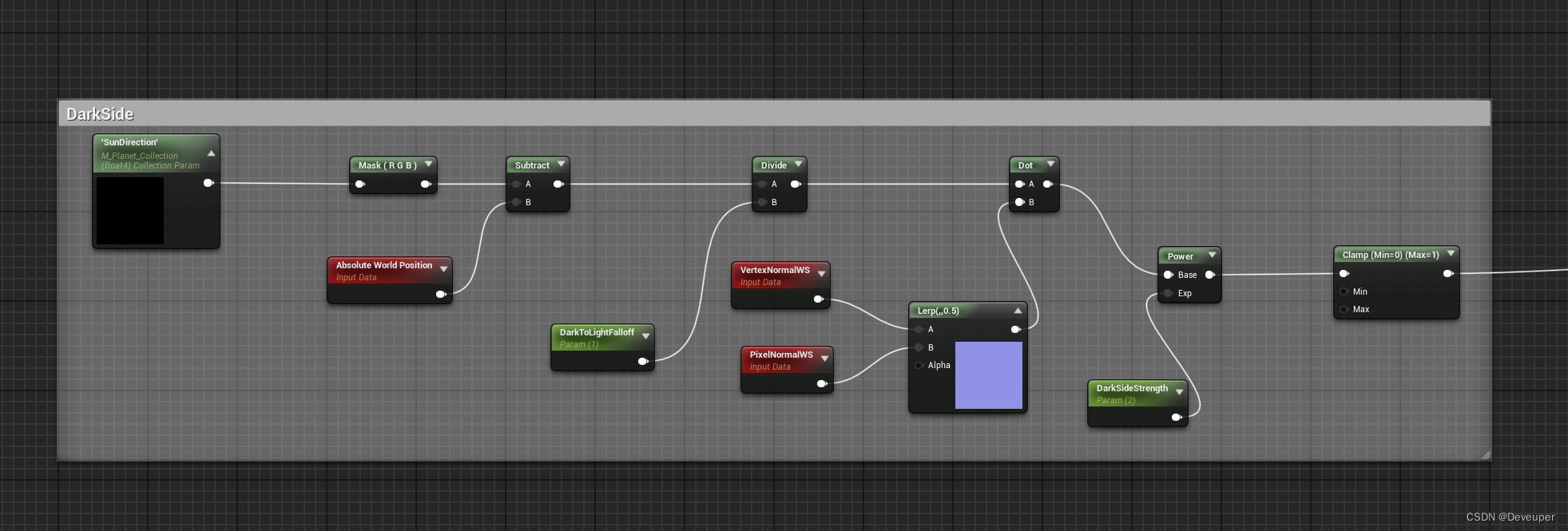
地球行星UE5和UE4
地球行星,包含多种地球风格,可蓝图控制自转和停止,可材质自转. 支持版本4.21-5.4版本 下载位置:https://mbd.pub/o/bread/ZpWZm5lv b站工坊:https://gf.bilibili.com/item/detail/1105582041 _______________________…...

7.k8s中的名称空间namespace
目录 一、Namespace(命名空间) 二、查看系统的名称空间 1.查看系统中的名称空间列表 2.单独查看一个名称空间下的对应资源 三、名称空间的管理 1.创建名称空间 1.1响应式创建 1.2声明式创建 2.删除名称空间 四、资源引用名称空间 一、Namespace(命名空间) 命名空间(Name…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
