结合场景,浅谈深浅度拷贝
有两段代码是这样的:
A段:
List<String> list1 = new ArrayList<>();
Bear B = new Bear();
for(Apple apple : apples){B.url = apple.url;B.content = apple.content;list1.add(Bear);
}B段:
List<String> list1 = new ArrayList<>();
for(Apple apple : apples){
Bear B = new Bear();B.url = apple.url;B.content = apple.content;list1.add(Bear);
}显而易见,这两段代码的区别在于Bear对象的创建的位置不同,第一段代码里面,先创建了一个 Bear 对象 B,然后在循环中不断更新 B 的属性,并将同一个 B 对象多次添加到 list1 中。由于 list1 中存储的是对象的引用,因此最终 list1 中存储的是多个指向同一个 Bear 对象的引用。
而第二段代码中,我们在每次循环中都创建了一个新的 Bear 对象 B,并将其添加到 list1 中。因此,list1 中存储的是多个不同的 Bear 对象的引用。
所以,其实两次list的存储的Bear对象结果会是不同的,第一段代码存了一堆一样的Bear,那么问题来了:我想不重复创建Bear对象,但是也能达到第二段效果,应该怎么做?
答案是使用深度拷贝;
在修复代码之前,深浅度拷贝的定义我们复习下:
浅拷贝(Shallow Copy):
- 浅拷贝是指在复制对象时,只复制对象本身和其内部引用的对象的引用,而不复制引用的对象本身。
- 在浅拷贝中,新对象和原对象共享内部引用的对象,即新对象和原对象的引用指向同一个内部对象。
- 如果原对象的属性是基本数据类型,那么浅拷贝会复制这些属性的值;如果原对象的属性是引用类型,那么浅拷贝只会复制引用,而不会复制引用指向的对象。
深度拷贝(Deep Copy):
- 深度拷贝是指在复制对象时,不仅复制对象本身,还会递归复制对象内部引用的对象,直到所有引用的对象都被复制。
- 在深度拷贝中,新对象和原对象的所有引用对象都是独立的,即新对象和原对象的引用指向不同的内部对象。
- 无论原对象的属性是基本数据类型还是引用类型,深度拷贝都会复制所有属性的值或引用指向的对象。
原理比较:
- 浅拷贝只复制对象本身和其内部引用的对象的引用,因此新对象和原对象共享内部引用的对象,可能会导致对象之间的状态相互影响。
- 深度拷贝会递归复制对象内部引用的对象,确保新对象和原对象的所有引用对象都是独立的,避免对象之间的状态相互影响。
那么好,我们基于该原理改造下我们的第一段代码:
首先需要重写Bear对象,重写clone方法:
public class Bear implement Clone{private String url;private String content;//构造函数等省略@Overridepublic Bear clone(){try{Bear cloned = (Bear) super.clone(); // 首先调用父类的 clone 方法进行浅拷贝// 对象的属性进行深度拷贝cloned.url = new String(this.url);cloned.content = new String(this.content);return cloned; }catch(CloneNotSupportedException e){throw new AssertionError();}}}写完Bear类的clone方法后,就可以用它的clone方法来做对象复制,最终第一段代码改写如下:
List<String> list1 = new ArrayList<>();
Bear originalBear = new Bear(); // 假设有一个原始的 Bear 对象
for(Apple apple : apples){Bear clonedBear = originalBear.clone(); // 使用克隆方法创建新的 Bear 对象clonedBear.url = apple.url;clonedBear.content = apple.content;list1.add(clonedBear);
}这样修改后,可以避免多次创建新对象,同时确保 list1 中加载不同的 Bear 对象。
相关文章:

结合场景,浅谈深浅度拷贝
有两段代码是这样的: A段: List<String> list1 new ArrayList<>(); Bear B new Bear(); for(Apple apple : apples){B.url apple.url;B.content apple.content;list1.add(Bear); } B段: List<String> list1 new A…...
生成指定范围的随机整数
private static final Random RANDOM new Random();// 生成指定范围的随机整数public static int generateRandomInt(int min, int max) {return RANDOM.nextInt(max - min 1) min;}public static void main(String[] args) {Integer count 5;Integer randomInt generateR…...

少的缓存穿透是缓存击穿,大量的是缓存雪崩
只要请求穿过了缓存层,直接打到了数据库,我就把这个现象理解为缓存穿透。 只要缓存失效了,就会出现缓存穿透,然后根据失效缓存数量的多少,划分出缓存击穿和缓存雪崩 缓存一致性 先改redis再改mysql。...

设备能耗数据在线监测
在追求可持续发展和绿色经济的当下,企业对于设备能耗的管理愈发重视。设备能耗数据在线监测,不仅能帮助企业实时掌握设备的运行状况,还能为企业节能减排、降低运营成本提供有力支持。HiWoo Cloud平台凭借其先进的技术和丰富的经验,…...

springboot整合websocket,超简单入门
springBoot整合webSocket,超简单入门 webSocket简洁 WebSocket 是一种基于 TCP 协议的全双工通信协议,它允许客户端和服务器之间建立持久的、双向的通信连接。相比传统的 HTTP 请求 - 响应模式,WebSocket 提供了实时、低延迟的数据传输能力。…...

代码随想录算法训练营第三十四天| 860.柠檬水找零 406.根据身高重建队列 452. 用最少数量的箭引爆气球
860.柠檬水找零 题目链接 思路 三种情况,一种贪心,在bill为20时,有一次贪心选择:优先考虑先找105,再考虑找3*5,因为5可以用于bill10和bill20两种情况 解题方法 第一种:bill5,直接收 第二种…...
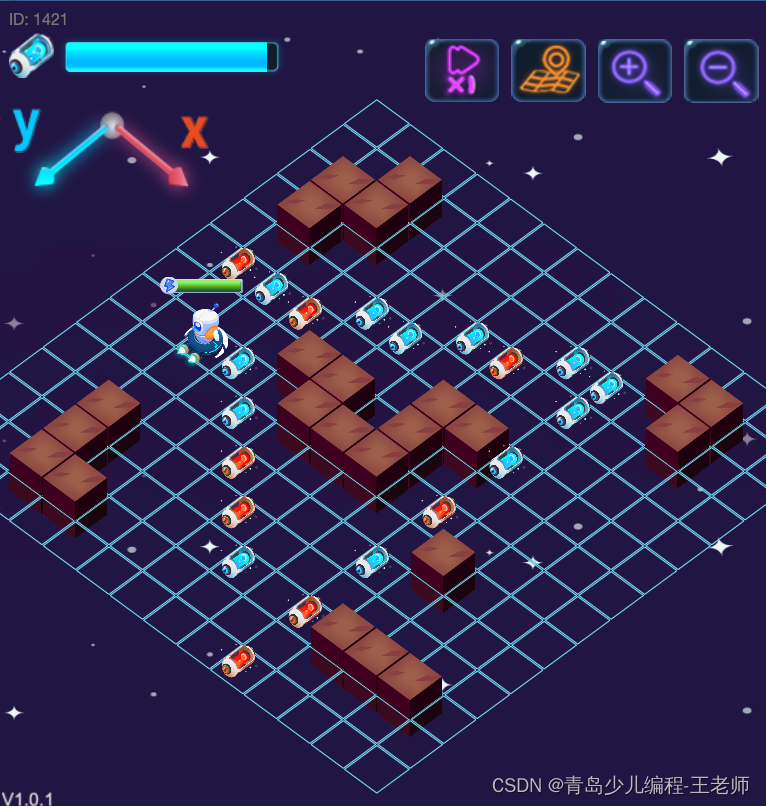
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2 1、 for i in range(3):Dev.step(3)Dev.turnRight()Dev.step(4)Dev.turnLeft()2、 for i in range(3):Spaceship.step(3)Spaceship.turnRight()Spaceship.step(1)3、 Dev.turnLeft() Dev.step(Dev.x - Item[1].…...

12.轻量级锁原理及其实战
文章目录 轻量级锁原理及其实战1.轻量级锁的核心原理2.轻量级锁的演示2.1.轻量级锁的演示代码2.2.结果分析 3.轻量级锁的分类3.1.普通自旋锁3.2.自适应自旋锁 4.轻量级锁的膨胀 轻量级锁原理及其实战 引入轻量级锁的主要目的是在多线程环境竞争不激烈的情况下, 通过…...
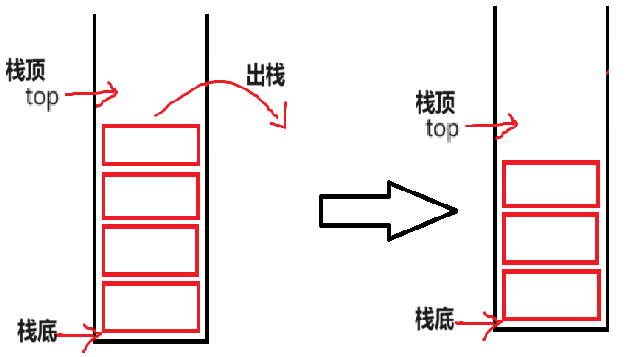
栈结构(c语言)
1.栈的概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈&am…...

【C++】C/C++中新const用法:const成员
欢迎来到CILMY23的博客 本篇主题为: C/C中新const用法:const成员 个人主页:CILMY23-CSDN博客 系列专栏:Python | C | C语言 | 数据结构与算法 | 贪心算法 | Linux 感谢观看,支持的可以给个一键三连,点赞…...

武汉凯迪正大—钢管焊缝裂纹探伤仪
产品概述 武汉凯迪正大无损探伤仪是一种便携式工业无损探伤仪器, 能够快速便捷、无损伤、精确地进行工件内部多种缺陷(裂纹、夹杂、气孔等)的检测、定位、评估和诊断。既可以用于实验室,也可以用于工程现场。 设置简单,…...

为什么 IP 地址通常以 192.168 开头?
在网络配置中,我们经常会遇到以 192.168 开头的 IP 地址,例如 192.168.0.1 或者 192.168.1.100。 这些地址通常用于局域网中,但为什么要选择以 192.168 开头呢? 本文将深入探讨这个问题,并解释其背后的原因和历史渊源…...

elementUi中的el-table合计行添加点击事件
elementUi 文档中,合计行并没有点击事件,这里自己实现了合计行的点击事件。 created() {this.propertyList [{ property: order, label: 序号 },{ property: deptName, label: 单位名称 },{ property: contentPublishQuantity, label: 文章数量 },{ pro…...

Zookeeper集群搭建的一些问题
问题描述一: Cannot open channel to 2 at election address /192.168.60.132:3888解决方案: 查看zookeeper配置文件zoo.cfg / zoo_sample.cfg中集群配置部分 server.1zoo1-net1:2888:3888|zoo1-net2:2889:3889 server.2zoo2-net1:2888:3888|zoo2-net2…...
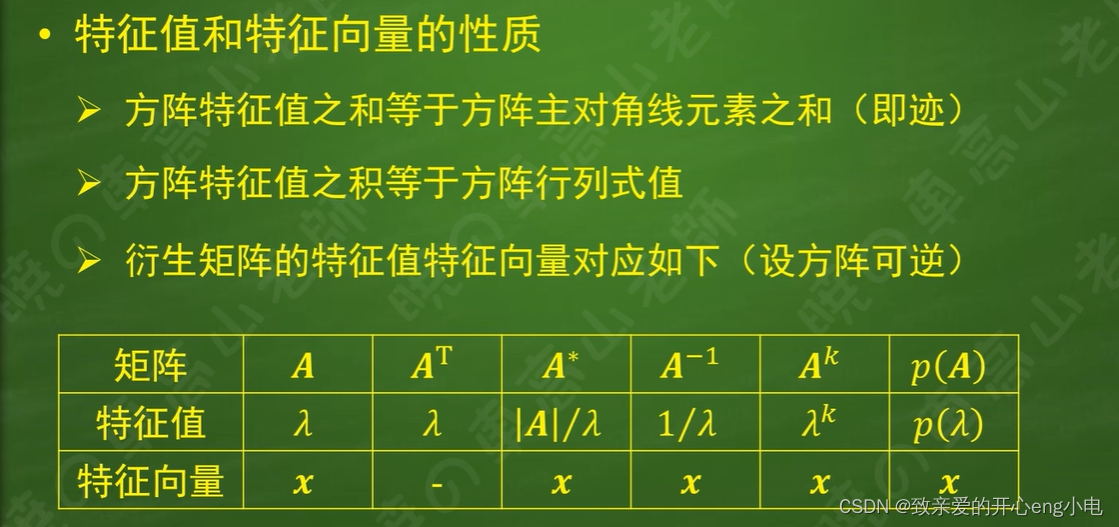
【线性代数】俗说矩阵听课笔记
基础解系的概念 线性方程组的解 21行列式和矩阵秩Rank的等价刻画 子式 标准型 利用子式求解矩阵的rank 24零积秩不等式 齐次线性方程组的基础解系 rank的两个重要结论 ¥25伴随矩阵的rank 奇异矩阵:行列式0的矩阵 31线性相关,线性无关&#…...

物联网技术在数字化工厂中的应用,你知道多少?——青创智通
工业物联网解决方案-工业IOT-青创智通 物联网(IoT)技术在数字化工厂的应用正日益成为工业革命的重要推动力。随着科技的飞速发展,物联网技术不断革新,其在数字化工厂中的应用也呈现出愈发广泛和深入的态势。本文将详细探讨物联网…...
nacos开启登录开关启动报错“Unable to start embedded Tomcat”
nacos 版本:2.3.2 2.2.2版本之前的Nacos默认控制台,无论服务端是否开启鉴权,都会存在一个登录页;在之后的版本关闭了默认登录页面,无需登录直接进入控制台操作。在这里我们可以在官网可以看到相关介绍 而我现在所用的…...
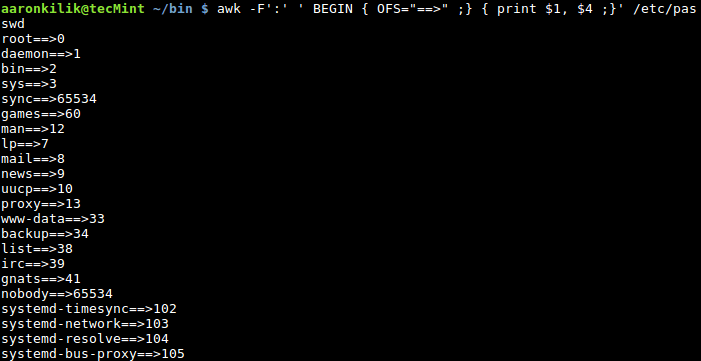
Linux|了解如何使用 awk 内置变量
引言 当我们揭开 Awk 功能部分时,我们将介绍 Awk 中内置变量的概念。您可以在 Awk 中使用两种类型的变量:用户定义的变量和内置变量。 内置变量的值已经在 Awk 中定义,但我们也可以仔细更改这些值,内置变量包括: FILEN…...

代码随想录-算法训练营day29【回溯算法05:递增子序列、全排列】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第七章 回溯算法part05* 491.递增子序列 * 46.全排列 * 47.全排列 II详细布置 491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 https://programmercarl.com…...

704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target&a…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
