【Linux】Centos7配置JDK
1.启动虚拟机、Xshell、Xftp
2.在Xshell中新建一个会话,用于连接到虚拟机中
3.因为虚拟机里自带有JDK,所以需要先卸载自带的JDK
3.1.查询已安装的 jdk 列表
rpm -qa | grep jdk

3.2.将查询到的全部删除
yum -y remove XXX(上面查询到的 jdk 名称)
需要一个一个的进行卸载,直到查询不到

4.上传安装包并进行解压
4.1创建文件夹 /usr/local/java
mkdir -p /usr/local/java
将Linux版JDK安装包通过Xftp上传至Linux中的/usr/local/java文件夹中
4.2.将 jdk 压缩包解压到 /usr/local/java 目录下,需要先切换到该目录下
cd /usr/local/java
tar -zxvf jdk-8u151-linux-x64.tar.gz -C /usr/local/java/

5.配置 jdk 的环境变量
vim /etc/profile
打开后

添加以下内容,保存并退出
# JAVAHOME
export JAVA_HOME=/usr/local/java/jdk1.8.0_151
export CLASSPATH=.:$JAVA_HOME/lib:$JAVA_HOME/jre/lib
export PATH=$PATH:$JAVA_HOME/bin
6.让配置文件生效
source /etc/profile
7.校验
java -version

相关文章:

【Linux】Centos7配置JDK
1.启动虚拟机、Xshell、Xftp 2.在Xshell中新建一个会话,用于连接到虚拟机中 3.因为虚拟机里自带有JDK,所以需要先卸载自带的JDK 3.1.查询已安装的 jdk 列表 rpm -qa | grep jdk3.2.将查询到的全部删除 yum -y remove XXX(上面查询到的 j…...

pytorch中统计一个数在tensor中出现了几次
pytorch中统计一个数在tensor中出现了几次 在PyTorch中,可以使用torch.eq()函数配合torch.sum()来统计某个数值在Tensor中出现的次数。torch.eq()函数会返回一个新的Tensor,其中对于每个元素来说,如果和指定的数值相等,则该位置为…...
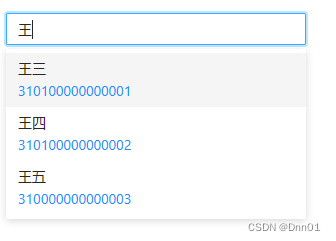
a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题
a-auto-complete 请求后端数据做模糊查询,解决下拉框选择选不上,不回显的问题 记录一个a-auto-complete卡bug卡了两天,找不到哪里的问题下拉框选择选不上,不回显,最后终于解决了。 我还对下拉框显示的内容做了小调整。…...

Leetcode—724. 寻找数组的中心下标【简单】
2024每日刷题(129) Leetcode—724. 寻找数组的中心下标 实现代码 class Solution { public:int pivotIndex(vector<int>& nums) {int sum accumulate(nums.begin(), nums.end(), 0);int prefix 0;for(int i 0; i < nums.size(); i) {i…...

C语言 | Leetcode C语言题解之第72题编辑距离
题目: 题解: static inline int Min(const int a, const int b, const int c) {int min (a < b) ? a : b;return (min < c) ? min : c; }int minDistance(char * word1, char * word2){int m strlen(word1), n strlen(word2);int dp[m 1][n…...

AI视频教程下载:零代码创建AI智能体、AI Agents和ChatGPT的Gpts
这门课程专注于提示工程的掌握,教你以精确的方式引导GPT,利用它们的生成能力产生卓越的AI驱动结果。一步一步地,你将学会创建多样化的GPT军团——每个都设计来满足特定的专业需求。 从提供个性化职业变更指导的职业教练AI,到以惊…...

汽车之家,如何在“以旧换新”浪潮中大展拳脚?
北京车展刚刚落幕,两重利好正主导汽车市场持续升温:新能源渗透率首破50%,以及以旧换新详细政策进入落地期。 图源:中国政府网 在政策的有力指引下,汽车产业链的各个环节正经历着一场深刻的“连锁反应”。在以旧换新的…...
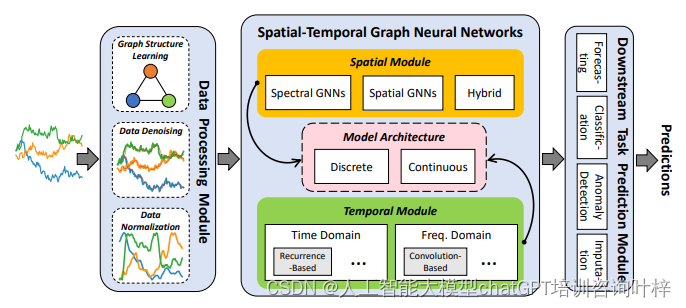
图神经网络(GNNs)在时间序列分析中的应用
时间序列数据是记录动态系统测量的主要数据类型,由物理传感器和在线过程(虚拟传感器)大量生成。时间序列分析对于解锁可用数据中隐含的丰富信息至关重要。随着图神经网络(GNNs)的最近进展,基于GNN的方法在时…...

Qt QShortcut快捷键类详解
1.简介 QShortcut是一个方便的工具类,用于在应用程序中创建快捷键。通过设置快捷键和关联的处理函数,可以实现快速执行某个操作的功能。 // 创建一个快捷键,关联到MyWidget类的keyPressEvent()函数 QShortcut *shortcut new QShortcut(QKe…...

003 redis分布式锁 jedis分布式锁 Redisson分布式锁 分段锁
文章目录 Redis分布式锁原理1.使用set的命令时,同时设置过期时间2.使用lua脚本,将加锁的命令放在lua脚本中原子性的执行 Jedis分布式锁实现pom.xmlRedisCommandLock.javaRedisCommandLockTest.java 锁过期问题1乐观锁方式,增加版本号(增加版本…...

Jackson工具,java对象和json字符串之间的互相转换
一、maven依赖引入jackson <dependency><groupId>com.fasterxml.jackson.core</groupId><artifactId>jackson-databind</artifactId><version>2.12.5</version></dependency>jackson-databind依赖见下: <depend…...

【设计模式】之装饰器模式
系列文章目录 【设计模式】之模板方法模式 【设计模式】之责任链模式 【设计模式】之策略模式 【设计模式】之工厂模式(三种) 前言 今天给大家介绍23种设计模式中的装饰器模式。🌈 一、什么是装饰器模式 装饰器模式(Decora…...

leetcode_46.全排列
46. 全排列 题目描述:给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2&#…...
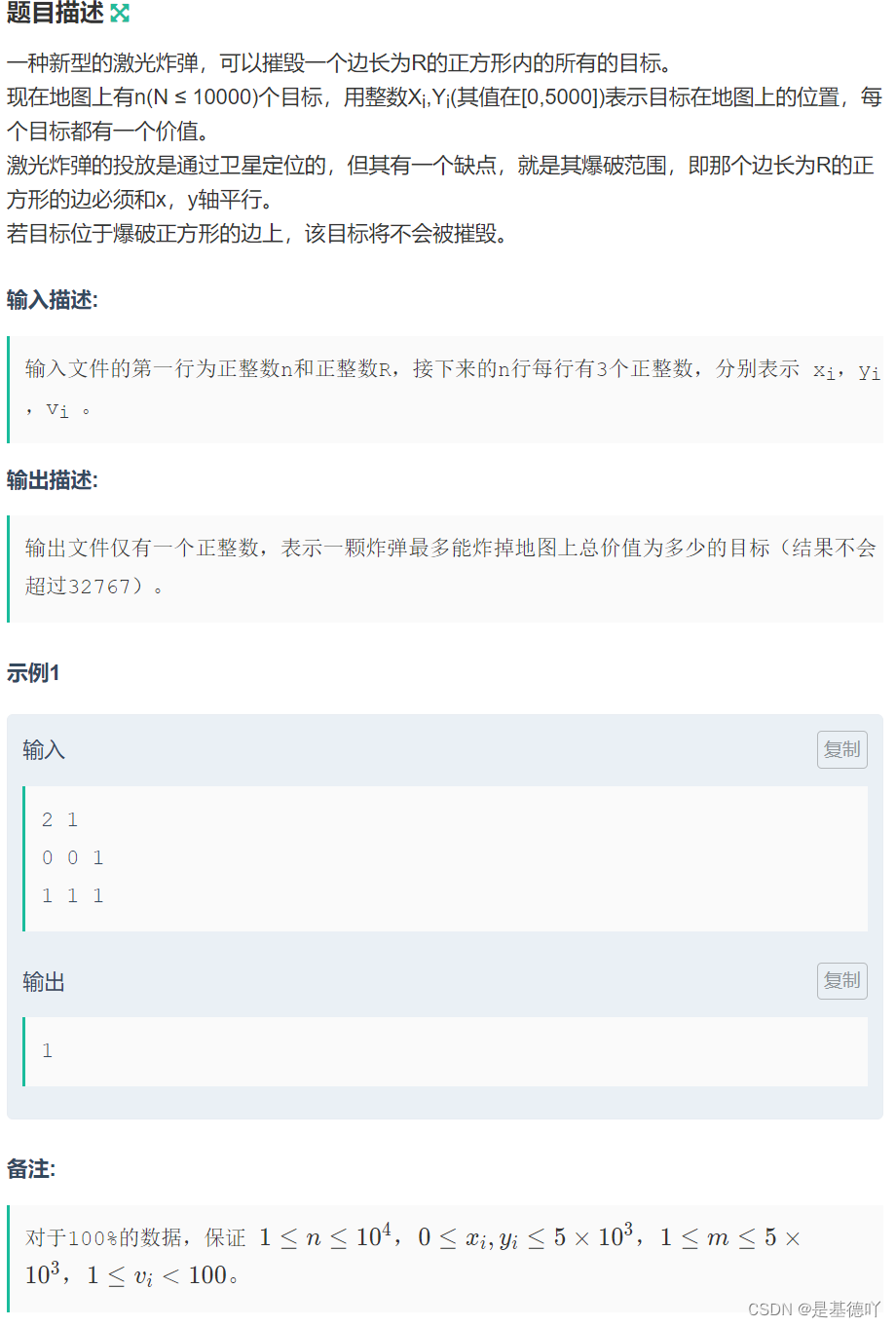
【牛客】[HNOI2003]激光炸弹
原题链接:登录—专业IT笔试面试备考平台_牛客网 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 二维前缀和板题。 注意从(1,1)开始存即可,所以每次输入x,y之后,要x,y。 因为m的范围最大为…...

Docker与Harbor:构建企业级私有Docker镜像仓库
目录 引言 一、本地私有仓库 (一)基本概述 (二)搭建本地私有仓库 1.下载registry镜像 2.启动容器 3.上传本地镜像 4.客户端下载镜像 二、Harbor简介 (一)什么是 Harbor (二ÿ…...

推荐几个傻瓜式短视频去水印在线网站
在数字化时代,短视频已成为信息传播的重要方式之一。随着TikTok、Instagram Reels、抖音等平台的流行,短视频的制作和分享成为了日常生活的一部分。然而,在分享或编辑这些短视频时,去除水印成为了一项不可或缺的需求。水印是视频原…...
大模型LLM之SFT微调总结
一. SFT微调是什么 在大模型的加持下现有的语义理解系统的效果有一个质的飞跃;相对于之前的有监督的Pre-Train模型;大模型在某些特定的任务中碾压式的超过传统nlp效果;由于常见的大模型参数量巨大;在实际工作中很难直接对大模型训…...
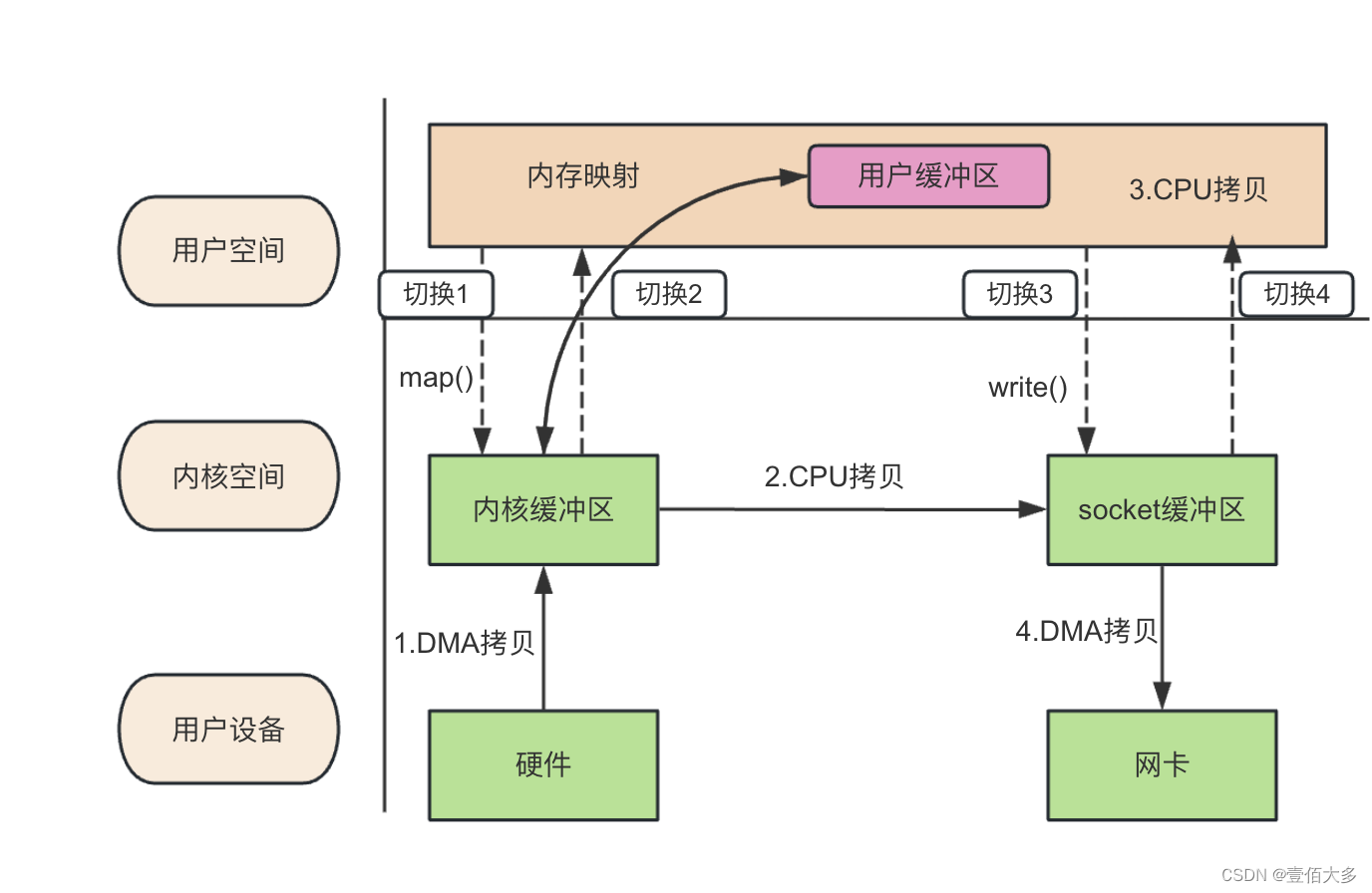
【RocketMQ问题总结-2】
RocketMQ 消息持久化 Broker通过底层的Netty服务器获取到一条消息后,会把这条消息的内容写入到一个CommitLog文件里去(一个Broker进程就只有一个CommitLog文件,也就是说这个Broker上所有Topic的消息都会写入这个文件)。 同时&…...

掌握Android Fragment开发之魂:Fragment的深度解析(上)
Fragment是Android开发中用于构建动态和灵活界面的基石。它不仅提升了应用的模块化程度,还增强了用户界面的动态性和交互性,允许开发者将应用界面划分为多个独立、可重用的部分,每个部分都可以独立于其他部分进行操作。本文将从以下几个方面深…...

深度解读DreamFusion:一站式AI解决方案
DreamFusion是一款备受瞩目的人工智能解决方案,它整合了多种AI技术,为用户提供了一站式的解决方案。本文将全面解读DreamFusion,探讨其特点、功能和应用场景,助您深入了解这一创新工具。 1. 特点概述 DreamFusion具备以下显著特…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
