代码随想录算法训练营第36期DAY19
DAY19
104二叉树的最大深度
根节点的高度就是最大深度。
非递归法:
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int maxDepth(TreeNode* root) {
- queue<TreeNode*> que;
- int md=0;
- if(root!=nullptr) que.push(root);
- while(!que.empty())
- {
- md++;
- int size=que.size();
- for(int i=0;i<size;i++)
- {
- TreeNode* node=que.front();
- que.pop();
- if(node->left) que.push(node->left);
- if(node->right) que.push(node->right);
- }
- }
- return md;
- }
- };
递归法:
核心:
- class Solution {
- public:
- int getdepth(TreeNode* node) {
- if (node == NULL) return 0;
- int leftdepth = getdepth(node->left); // 左
- int rightdepth = getdepth(node->right); // 右
- int depth = 1 + max(leftdepth, rightdepth); // 中
- return depth;
- }
- int maxDepth(TreeNode* root) {
- return getdepth(root);
- }
- };
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int geth(TreeNode* root)
- {
- if(root==nullptr) return 0;//叶子之下的,高度为0
- return 1+max(geth(root->left),geth(root->right));
- }
- int maxDepth(TreeNode* root) {
- return geth(root);
- }
- };
559 n叉树的最大深度
递归,非递归写过了,不写了:
- /*
- // Definition for a Node.
- class Node {
- public:
- int val;
- vector<Node*> children;
- Node() {}
- Node(int _val) {
- val = _val;
- }
- Node(int _val, vector<Node*> _children) {
- val = _val;
- children = _children;
- }
- };
- */
- class Solution {
- public:
- int maxDepth(Node* root) {
- if(root==nullptr) return 0;
- int depth=0;
- for(int i=0;i<root->children.size();i++)
- {
- depth=max(depth,maxDepth(root->children[i]));
- }
- return depth+1;
- }
- };
111二叉树的最小深度
非递归法:
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int minDepth(TreeNode* root) {
- int ld=0;
- queue<TreeNode*> que;
- if(root!=nullptr) que.push(root);
- while(!que.empty())
- {
- int size=que.size();
- ld++;
- for(int i=0;i<size;i++)
- {
- TreeNode* node=que.front();
- que.pop();
- if(node->left) que.push(node->left);
- if(node->right) que.push(node->right);
- if(node->left==nullptr&&node->right==nullptr) return ld;
- }
- }
- return ld;
- }
- };
递归法:
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- //后序遍历
- int getd(TreeNode* root)
- {
- if(root==nullptr) return 0;
- int leftd=getd(root->left);
- int rightd=getd(root->right);
- //中
- if(root->left==nullptr&&root->right!=nullptr) return 1+rightd;
- if(root->left!=nullptr&&root->right==nullptr) return 1+leftd;
- return 1+min(leftd,rightd);
- }
- int minDepth(TreeNode* root) {
- return getd(root);
- }
- };
222完全二叉树的节点个数
层序遍历法:
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int countNodes(TreeNode* root) {
- int res=0;
- queue<TreeNode*> que;
- if(root!=nullptr) que.push(root);
- while(!que.empty())
- {
- int size=que.size();
- res+=size;
- for(int i=0;i<size;i++)
- {
- TreeNode* node=que.front();
- que.pop();
- if(node->left) que.push(node->left);
- if(node->right) que.push(node->right);
- }
- }
- return res;
- }
- };
递归法:
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int countNodes(TreeNode* root) {
- if(root==nullptr) return 0;
- return 1+countNodes(root->left)+countNodes(root->right);
- }
- };
从完全二叉树的定义入手:
来自代码随想录:
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,就说明是满二叉树。
代码;
- /**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
- class Solution {
- public:
- int fulltree(TreeNode* root)
- {
- if(root==nullptr) return 0;
- TreeNode* left=root->left;
- TreeNode* right=root->right;
- int leftdepth=0,rightdepth=0;
- //求左子树深度
- while(left)
- {
- left=left->left;
- leftdepth++;
- }
- while(right)
- {
- right=right->right;
- rightdepth++;
- }
- if(leftdepth==rightdepth) return (2<<leftdepth)-1;
- //如果没找到满二叉树,就继续向左向右递归(后序遍历)+1表示中节点
- return fulltree(root->left)+fulltree(root->right)+1;
- }
- int countNodes(TreeNode* root) {
- return fulltree(root);
- }
- };


总结
深度:任意节点与根节点的距离(从1开始,也就是:根节点深度是1);用前序遍历来求,
高度:任意节点到叶子节点的距离。用后序遍历来求。(找叶子:要把孩子的信息返回给节点,所以用后序遍历)。根节点的高度就是二叉树的最大深度。
记忆:深根(前序) 高叶(后序)
写前序是比较麻烦的。一般写后序了。
相关文章:

代码随想录算法训练营第36期DAY19
DAY19 104二叉树的最大深度 根节点的高度就是最大深度。 非递归法: /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) …...
C#图像:1.图像区域分割与提取
(1)创建一个名为SplitImage的窗体的应用程序,将窗体改名为FormSplitImage。 (2)创建一个名为ImageProcessingLibrary的类库程序,为该工程添加名为ImageProcessing的静态类 (3)为Imag…...
炸弹使用技巧
掼蛋掼蛋,打的就是炸弹。炸弹是指掼蛋中由4-8张相同牌点的牌组成的牌型,需要注意的是:每局牌中都有两张红桃的牌型为逢人配,可以配除了大小王以外的任意牌,因此掼蛋中牌数最多的炸弹可以达到10张。 两副扑克牌中&#…...
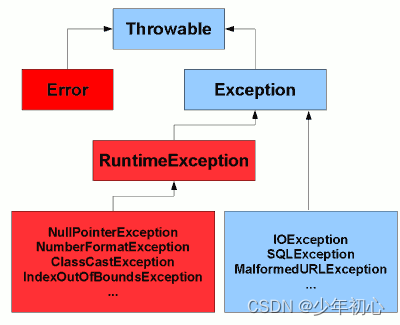
SpringAop详解
文章目录 一、Spring自定义注解1、什么是注解👨🏫2、注解的目的或作用💞3、JDK内置注解💫 【内置元注解 一共八个固定注解】4、元注解 🎯5、自定义注解📸5、Java反射API和类加载过程51、什么是反射基本原…...
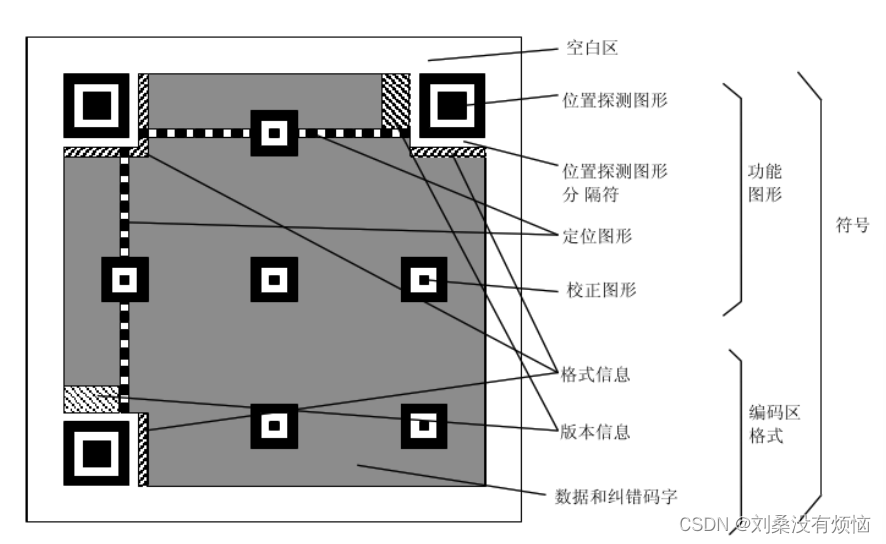
对XYctf的一些总结
对XYctf的一些总结 WEB 1.http请求头字段 此次比赛中出现的: X-Forwarded-For/Client-ip:修改来源ip via:修改代理服务器 还有一些常见的字段: GET:此方法用于请求指定的资源。GET请求应该安全且幂等,…...

Visual Studio和Visual Studio Code适用于哪些编程语言
Visual Studio和Visual Studio Code都适用于多种编程语言,它们的适用编程语言如下: Visual Studio适用于: C#Visual Basic .NETF#CJavaScriptTypeScriptPythonHTML/CSSJava(通过插件支持) Visual Studio Code适用于…...
缓存菜品操作
一:问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大。 二:实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: 每个分…...

达梦数据库常用命令整理
1.数据库自身信息 1.1 查询实例信息 SQL> select name inst_name from v$instance;行号 INST_NAME ---------- --------- 1 DMSERVER已用时间: 11.211(毫秒). 执行号:15.1.2 查询数据库当前状态 SQL> select status$ from v$instance;行号 STATUS$ -…...
Vue 组件的三大组成部分
Vue 组件通常由三大组成部分构成:模板(Template)、脚本(Script)、样式(Style) 模板部分是组件的 HTML 结构,它定义了组件的外观和布局。Vue 使用基于 HTML 的模板语法来声明组件的模…...

MoneyPrinter中的文字转声音国内替换方案
背景: 在进行MoneyPrinter项目国内环境搭建中,发现框架本身的TikTok文字转语音部分的代码已经不能用了,最好是能够找到国内网站的替换方案。 实现: 感谢网站:https://www.text-to-speech.cn/ 代码: # -*…...
消除试卷手写笔迹的软件免费的有哪些?这几款都不错
消除试卷手写笔迹的软件免费的有哪些?在数字化学习的浪潮中,学生们越来越频繁地利用电子设备来完成学习任务。然而,当纸质试卷需要被数字化并再次利用时,如何高效地消除手写笔迹便成为了一个有待解决的问题。那么,今天…...

智能创作时代:AI 如何重塑内容生成游戏规则
文章目录 前言一:自动化内容生成文章生成视频制作音频创作 二:内容分发与推广智能推荐系统社交媒体优化 三:内容分析与优化数据分析用户反馈质量控制 结语 前言 在数字化时代的浪潮中,内容生产与消费已成为信息传播的核心。随着人…...

大数据------JavaWeb------Tomcat(完整知识点汇总)
Web服务器——Tomcat Web服务器定义 它是一个应用程序(软件),对HTTP协议的操作进行封装,使得程序员不必直接对协议进行操作,让Web开发更便捷 Web服务器主要功能 封装HTTP协议操作,简化开发将Web项目部署到…...

LMDeploy笔记
随谈模型部署 模型部署包含的内容很多,来聊聊。 访存bottleneck 首先,基于transformer的计算是访存密集型任务。 so? 过去,我们表达模型的性能,通常会用ops,macs这些指标,也计算量来衡量模型的推理时间ÿ…...

Unity 状态机
文章目录 前言一、状态机二、应用1、场景切换2、人物行为切换3、宝箱、机关切换4、AI 三、人物行为总结 前言 提到Unity状态机,接触不久的开发者会想到Unity的动画状态机,而对于老油条来说,可能会回忆起自己实现的动画状态机。当然ÿ…...

一毛钱不到的FH8208C单节锂离子和锂聚合物电池一体保护芯片
前言 目前市场上电池保护板,多为分体方案,多数场合使用没有问题,部分场合对空间有进一步要求,或者你不想用那么多器件,想精简一些,那么这个芯片就很合适,对于充电电池来说,应在使用…...
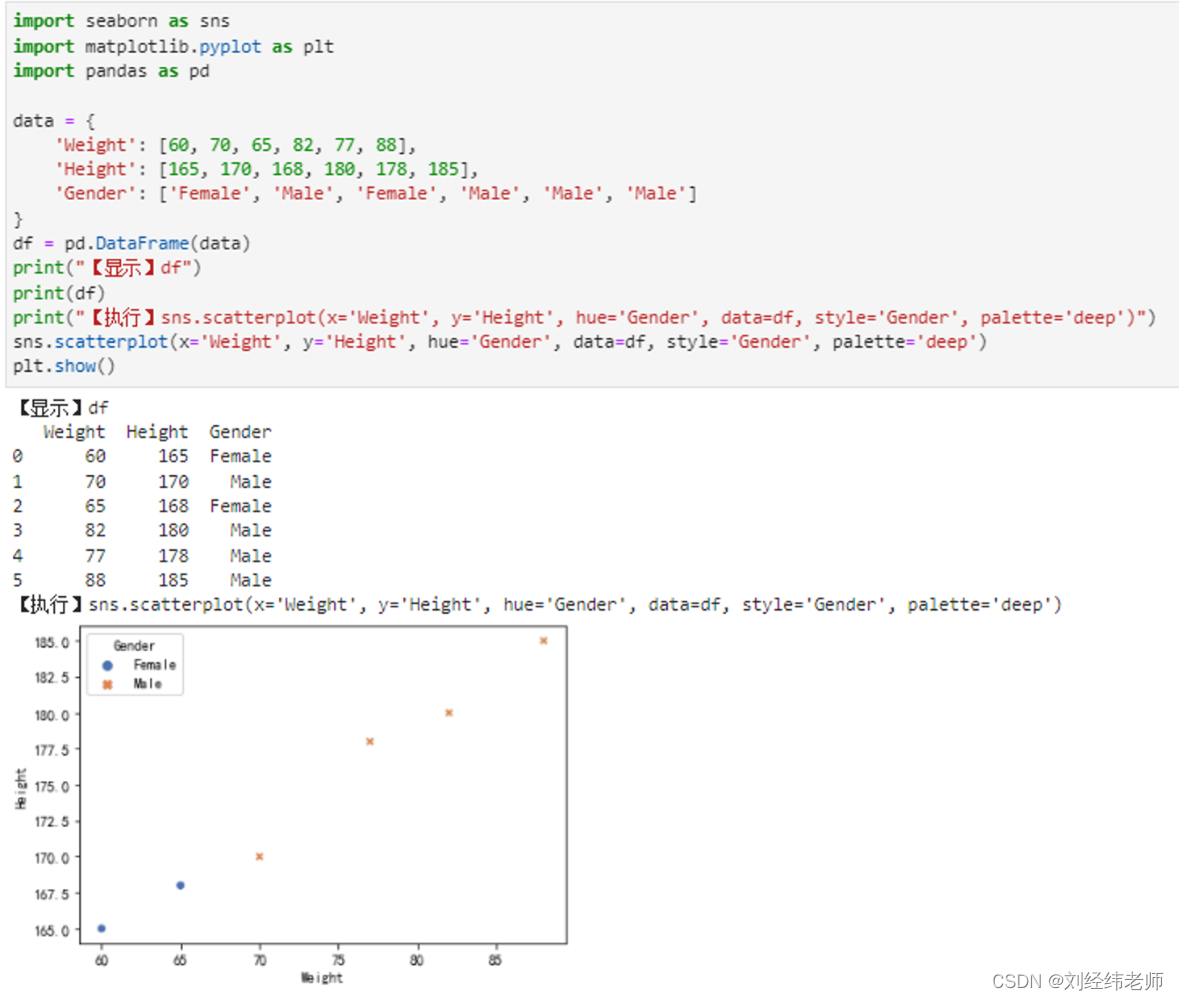
python数据可视化:显示两个变量间的关系散点图scatterplot()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 python数据可视化: 显示两个变量间的关系 散点图 scatterplot() [太阳]选择题 请问关于以下代码表述错误的选项是? import seaborn as sns import matplotlib.pyplot …...

【QT教程】QT6硬件高级编程入门 QT硬件高级编程
QT6硬件高级编程入门 使用AI技术辅助生成 QT界面美化视频课程 QT性能优化视频课程 QT原理与源码分析视频课程 QT QML C扩展开发视频课程 免费QT视频课程 您可以看免费1000个QT技术视频 免费QT视频课程 QT统计图和QT数据可视化视频免费看 免费QT视频课程 QT性能优化视频免费看…...
)
Android 蓝牙实战——蓝牙电话通话状态同步(二十四)
前面分析了蓝牙电话通话状态的广播,我们可以在蓝牙电话中实时监听蓝牙电话的状态,但如果是其他音乐类 APP 呢,在播放的时候也需要知道当前是否有通话正在进行,但是有完全没必要实时监听电话的状态,这就需要一个获取通话状态的方法。 一、通话状态处理 1、CallsManager …...
docker 指定根目录 迁移根目录
docker 指定根目录 迁移根目录 1、问题描述2、问题分析3、解决方法3.1、启动docker程序前就手动指定docker根目录为一个大的分区(支持动态扩容),事前就根本上解决根目录空间不够问题3.1.0、方法思路3.1.1、docker官网安装文档3.1.2、下载docker安装包3.1.3、安装doc…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
