暴力法解决最近对问题和凸包问题-实现可视化
目录
最近对问题
凸包问题
最近对问题
顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。
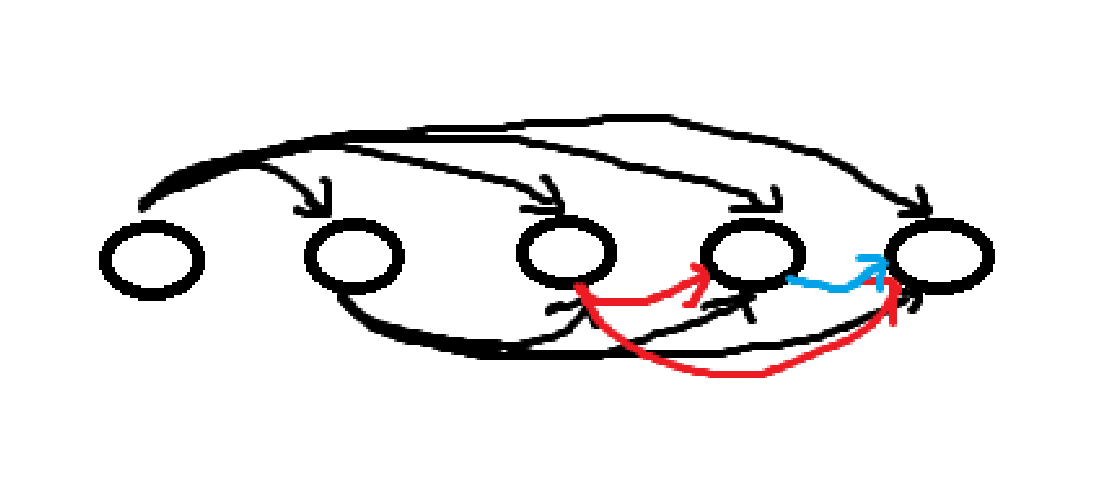
大概思路就是如图(每个圈代表一个数对)
第一个和其他四个比较
第二个和其他三个比较
.......
最后比较最小的
代码
图形化界面主要是easyx的graphics
#include<iostream>
#include <fstream>
#include<graphics.h>
#include <conio.h>
using namespace std;
#define Max 20 //20个点的凸包问题
#define maxn 10000
#define time 15
typedef struct {int a;int b;
}point;
void draw_point(point x[]);
void draw_line(int a, int b, int c, int d);
void judge(point x[]);
int main() {point x[Max];
ifstream in("a.txt");cout << "从txt中读取点坐标如下:" << endl;for (int i = 0; i < 20; i++){in >> x[i].a;in >> x[i].b;}for (int i = 0; i < 20; i++){cout << i + 1 << ":" << "(" << x[i].a << "," << x[i].b << ")" << endl;}cout << endl << endl;in.close();cout << "存储的数据如下:" << endl;draw_point(x);judge(x);getchar();return 0;
}
void judge(point x[]) {int i, j, a, b, c, n, num1 = 0, num2 = 0;int flag;for (i = 0; i < Max; i++){for (j = i + 1; j < Max; j++){b = x[i].a - x[j].a;a = x[j].b - x[i].b;c = x[i].a * x[j].b - x[j].a * x[i].b;
for (n = 0; n < Max; n++){if (n != i && n != j){flag = x[n].a * a + x[n].b * b;if (flag < c)num1++;else if (flag > c)num2++;else {num1++;num2++;};}}if (num1 == 18 || num2 == 18){cout << "如下两点是极边:" << "(" << x[i].a << "," << x[i].b << ")" << "(" << x[j].a << "," << x[j].b << ")" << endl;draw_line(x[i].a, x[i].b, x[j].a, x[j].b);}num1 = num2 = 0;}}
}
void draw_point(point x[]) {initgraph(880, 680, SHOWCONSOLE);setorigin(320, 240);int a, b;for (int i = 0; i < Max; i++) {a = x[i].a * time;b = x[i].b * time;fillcircle(a, b, 4);}
}
void draw_line(int a, int b, int c, int d)
{line(a * time, b * time, c * time, d * time);
}运行结果
先写一个a.txt文件的点(20个)

运行(可视化界面)

凸包问题
凸包问题就是在一个有n个点集的平面上,找出所有的“极点”,这些极点所构成的边界能够把其他所有的点都能包含在内。
思路
由两个点连起来的直线会将平面分成两部分,其中半个平面的点都满足ax+by>c ,另一半平面中的点都满足ax+by<c ,对于线上的点来说满足ax+by=c。因此,算法的思路就是对于每个点带入ax+by-c,判断表达式结果的符号是否相同即可。
代码
#include<iostream>
#include<fstream>
#include<graphics.h>
#include<cmath>
#include<algorithm>
using namespace std;
#define Max 20 // 最大点数
#define maxn 10000
#define time 15
typedef struct {int a;int b;
} point;
void draw_point(point x[]);
void draw_line(int a, int b, int c, int d);
void closest_pair(point x[]);
int main() {point x[Max];
ifstream in("points.txt");
cout << "从txt文件中读取点坐标:" << endl;for (int i = 0; i < Max; i++) {in >> x[i].a;in >> x[i].b;}for (int i = 0; i < Max; i++) {cout << i + 1 << ": (" << x[i].a << ", " << x[i].b << ")" << endl;}cout << endl << endl;in.close();
cout << "存储的数据如下:" << endl;draw_point(x);closest_pair(x);getchar();closegraph(); // 关闭图形窗口return 0;
}
void closest_pair(point x[]) {int min_distance = INT_MAX;int pair1 = -1, pair2 = -1;
for (int i = 0; i < Max; i++) {for (int j = i + 1; j < Max; j++) {int distance = pow(x[i].a - x[j].a, 2) + pow(x[i].b - x[j].b, 2);if (distance < min_distance) {min_distance = distance;pair1 = i;pair2 = j;}}}
cout << "最近的点对:" << endl;cout << "(" << x[pair1].a << ", " << x[pair1].b << ") 和 (" << x[pair2].a << ", " << x[pair2].b << ")" << endl;
// 绘制最近的点对连线draw_line(x[pair1].a, x[pair1].b, x[pair2].a, x[pair2].b);
}
void draw_point(point x[]) {initgraph(880, 680, SHOWCONSOLE);setorigin(320, 240);int a, b;for (int i = 0; i < Max; i++) {a = x[i].a * time;b = x[i].b * time;fillcircle(a, b, 4);}
}
void draw_line(int a, int b, int c, int d) {line(a * time, b * time, c * time, d * time);
}运行结果
先写一个points.txt文件的点(20个)

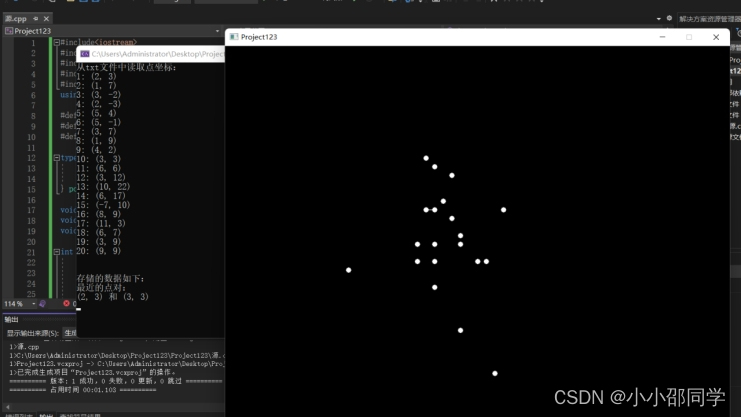
运行:(可视化界面)
相关文章:

暴力法解决最近对问题和凸包问题-实现可视化
目录 最近对问题 凸包问题 最近对问题 顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。 大概思路就是如图(每个圈代表一个数对) 第一个和其他四个比较 第二个和其他三个比较 …...
[Kubernetes] Rancher 2.7.5 部署 k8s
server: 192.168.66.100 master: 192.168.66.101 node1: 192.168.66.102 文章目录 1.rancher server 安装docker2.部署k8s3.kubeconfig4.测试集群 1.rancher server 安装docker 所有主机开通ipv4 vi /etc/sysctl.conf#加入 net.ipv4.ip_forward 1#配置生效 sysctl -prancher…...
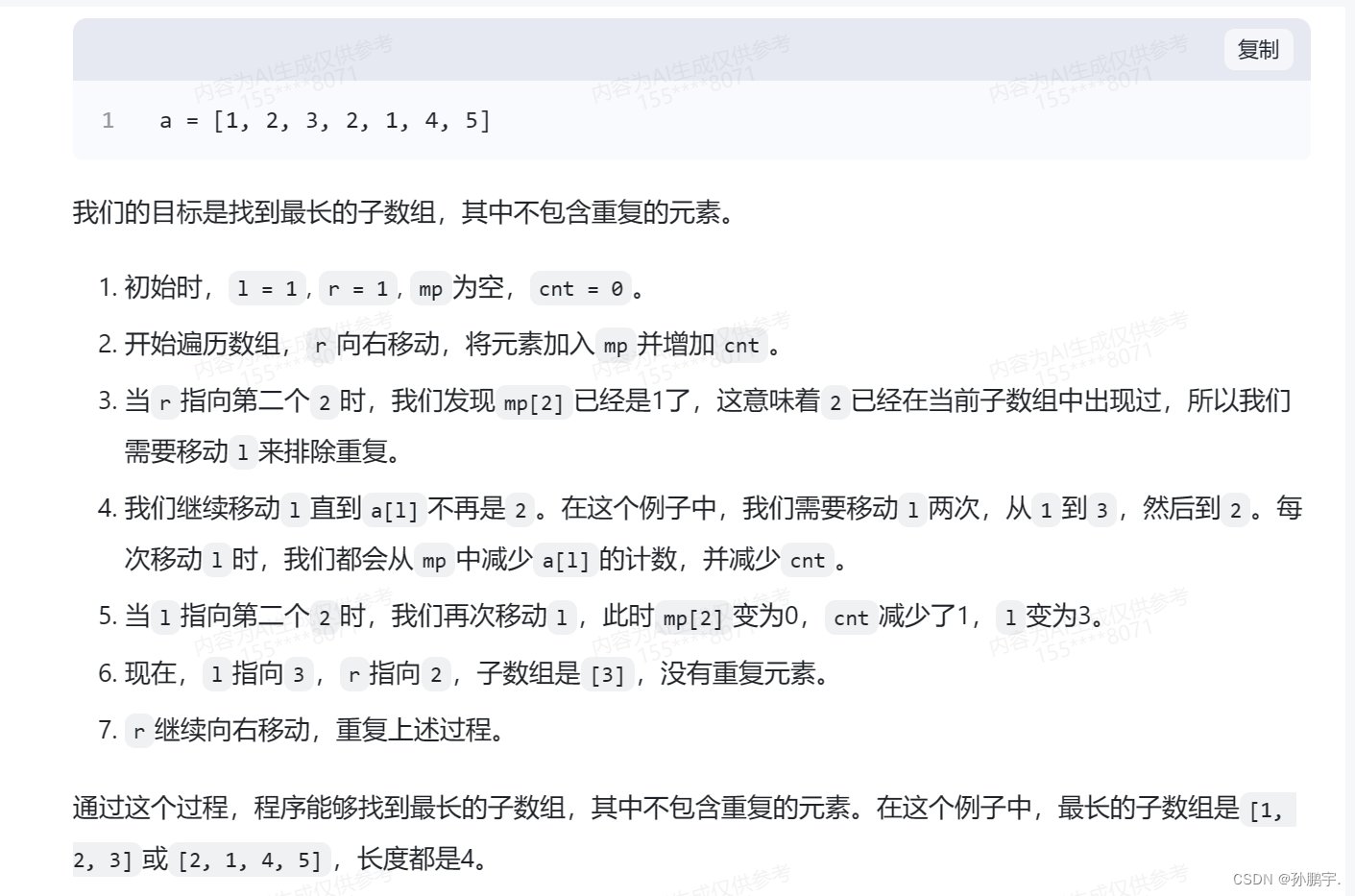
码题杯 世界警察 思想:双指针
https://www.matiji.net/exam/brushquestion/4/4446/16A92C42378232DEB56179D9C70DC45C 双指针 思路是这样的,首先r指针向右走,如果r指针遇到了和l指针一样的,那么l指针就,一直加到r指针的位置,此时a[l]a[r]࿰…...
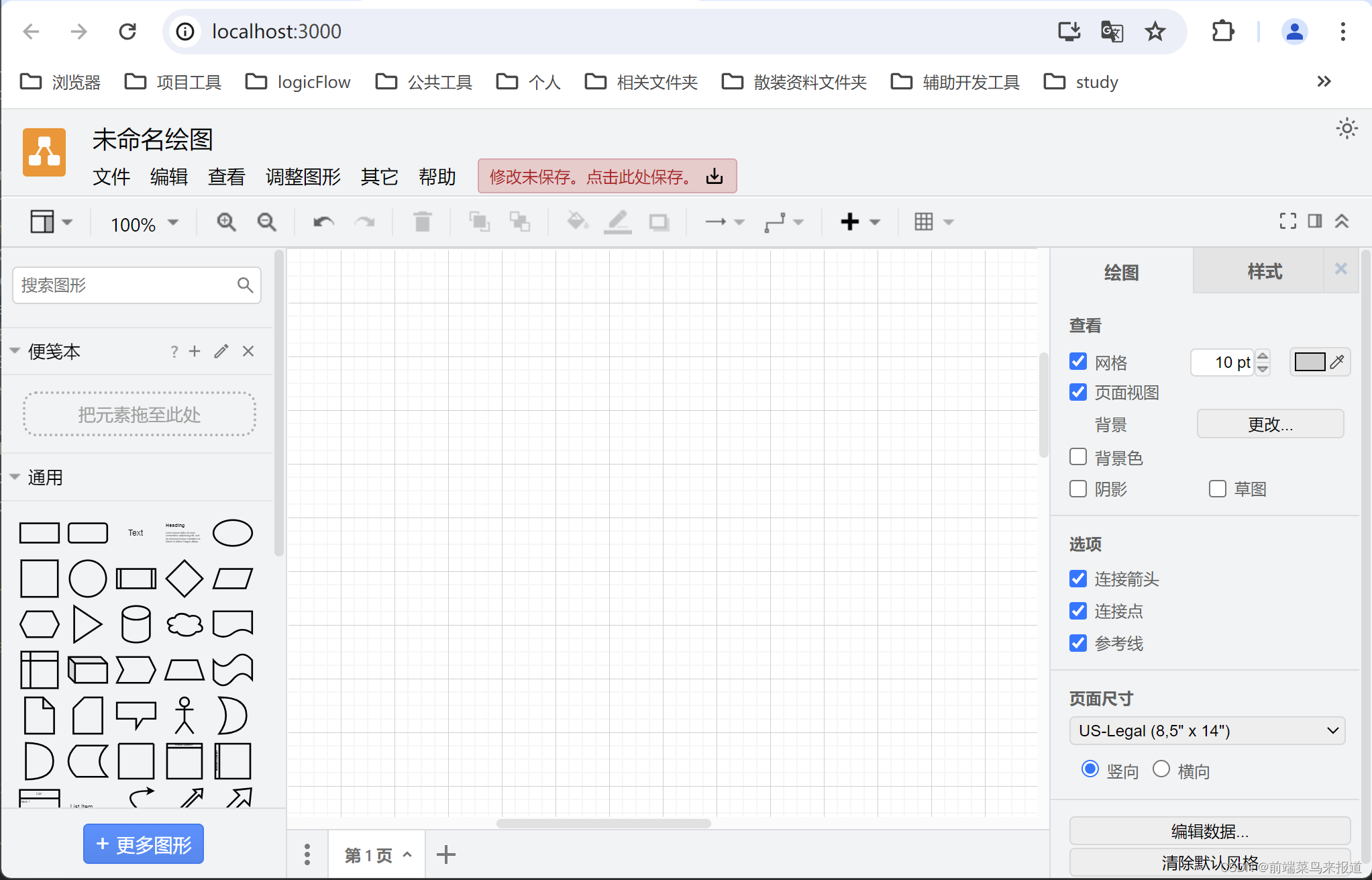
drawio 网页版二次开发(1):源码下载和环境搭建
目录 一 说明 二 源码地址以及下载 三 开发环境搭建 1. 前端工程地址 2. 配置开发环境 (1)安装 node.js (2)安装 serve 服务器 3. 运行 四 最后 一 说明 应公司项目要求,需要对drawio进行二次开发&…...

算法训练Day33 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 class Solution { public:int fib(int n) {if(n<1) return n;int pre2 0;int pre1 1;int result 0;for(int i2; i<n; i ){result pre1pre2;pre2 pre1;pre1 result;}return result;} };参考文章:代码随想录- 509. 斐波那契数 70. 爬楼梯…...
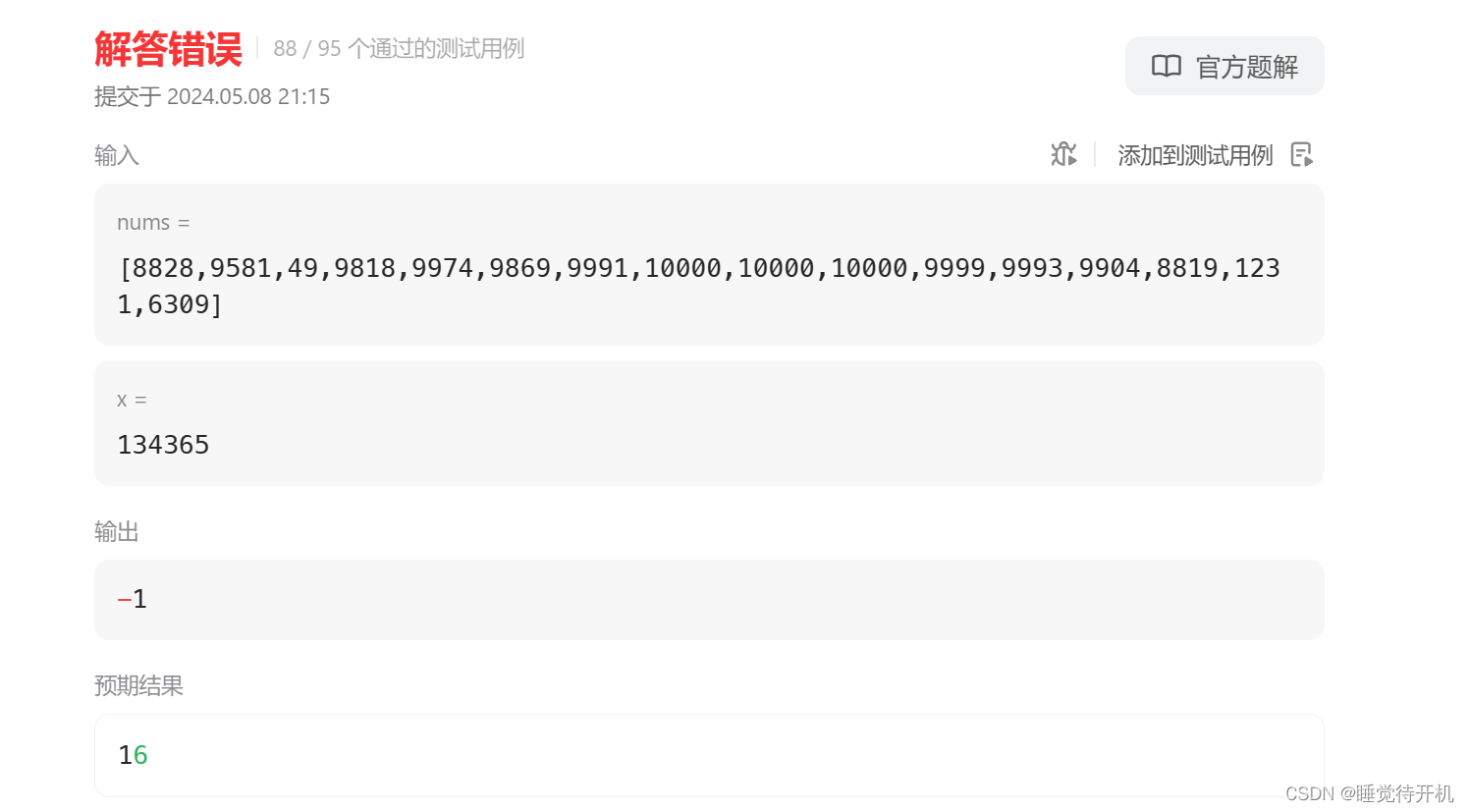
【算法】滑动窗口——将x减到0的最小操作数
本节博客主要是讲的我解“将x减到0的最小操作数”这道题的思路历程,从最开始的想法到代码提交的详细记录,有需要借鉴即可。 目录 1.题目2.代码示例3.细节3.1left越界3.2特殊情况 4.总结 1.题目 题目链接:LINK 看题目意思是就是给你一个数X&…...

《引爆流量获客技术》实操方法,手把手教你搭建盈利流量池
[1]-先导课.mp4 [2]-第1节:设计客户终身价值的方法和买客户思维.mp4 [3]-第2节:【渠道模型】解决谁是我的客户如何找到.mp4 [4]-第3节:【诱饵模型】解决 如何获得更多的客户.mp4 [5]-第4节:【钩子模型】解决让目标客户主动找你…...
【记录】常见的前端设计系统(Design System)
解释一下设计系统的定义,以及在国内,都有那些优秀的设计系统可以学习,希望可以帮到大家。 什么是设计系统(Design System)? 设计系统(Design System)是一套综合性的指导原则、组件和规则&…...

如何使用Whisper音频合成模型
Whisper 是一个通用语音识别模型,由 OpenAI 开发。它可以识别多种语言的语音,并将其转换为文本。Whisper 模型采用了深度学习技术,具有高准确性和鲁棒性。 1、技术原理及架构 Whisper 的工作原理:音频被分割成 30 秒的片段&#…...
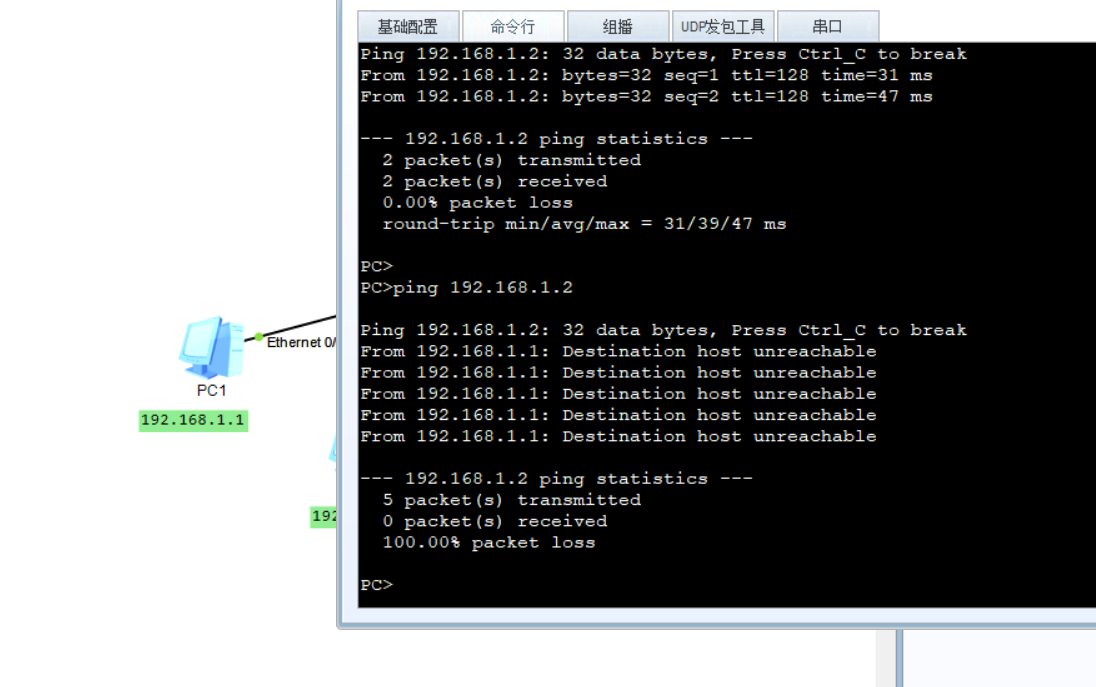
网络相关笔记
IPv4地址 IPv4地址通常以“点分十进制”形式书写,即四个0-255之间的十进制数,各数之间用英文句点(.)分隔,例如:192.0.2.1。总共32位的地址空间可以表示大约42亿个不同的地址。 IPv4地址结构包括ÿ…...

由C# yield return引发的思考
前言 当我们编写 C# 代码时,经常需要处理大量的数据集合。在传统的方式中,我们往往需要先将整个数据集合加载到内存中,然后再进行操作。但是如果数据集合非常大,这种方式就会导致内存占用过高,甚至可能导致程序崩溃。 …...

【问题解决】EasyExcel导出数据,并将数据中的实体类url转为图片
EasyExcel导出数据,并将数据中的实体类url转为图片 在导出excel数据时,用户要求把存储二维码url转为图片保存,然后研究了一下具体实现。 代码展示: public void exportData(String pointName, String districtName, String str…...
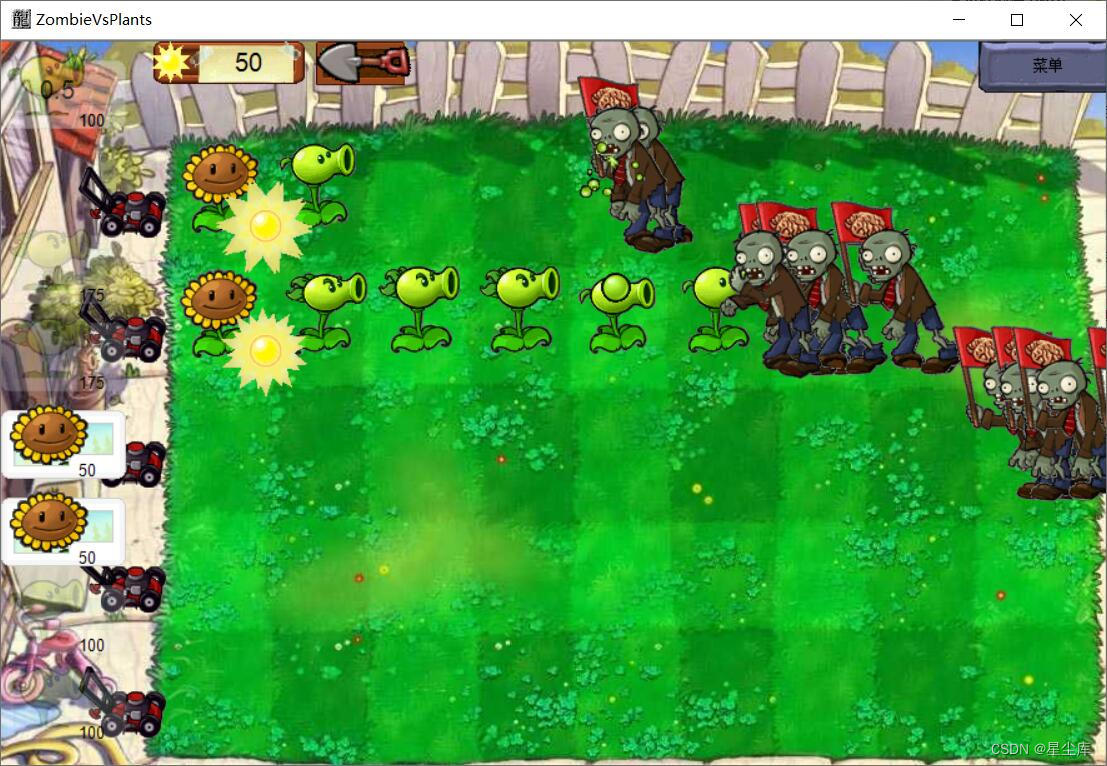
winform植物大战僵尸
winform植物大战僵尸 植物大战僵尸源码 半成品 需要的拿去学习 登陆注册选择关卡 向日葵 豌豆射手 双枪豌豆射手 项目获取: 项目获取:typora: typora/img (gitee.com) 备用项目获取链接1:yifeiyixiang/kamo: 源码下载 (github.com) 备用…...

Pointnet++改进即插即用系列:全网首发UIB轻量化模块
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入UIB,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3 步骤三...

【视频格式转换】【ffmepg】对mp4文件进行重新编码输出新的mp4文件
【视频格式转换】【ffmepg】对mp4文件进行重新编码输出新的mp4文件 背景 之前开发调试了个能正常调用ffmpeg解码mp4文件得到yuv数据的testbed(把ffmpeg开源库移植并交叉编译到一个嵌入式平台),用了好几年了,今天用来挂测一批新的采集视频mp4文件&#x…...
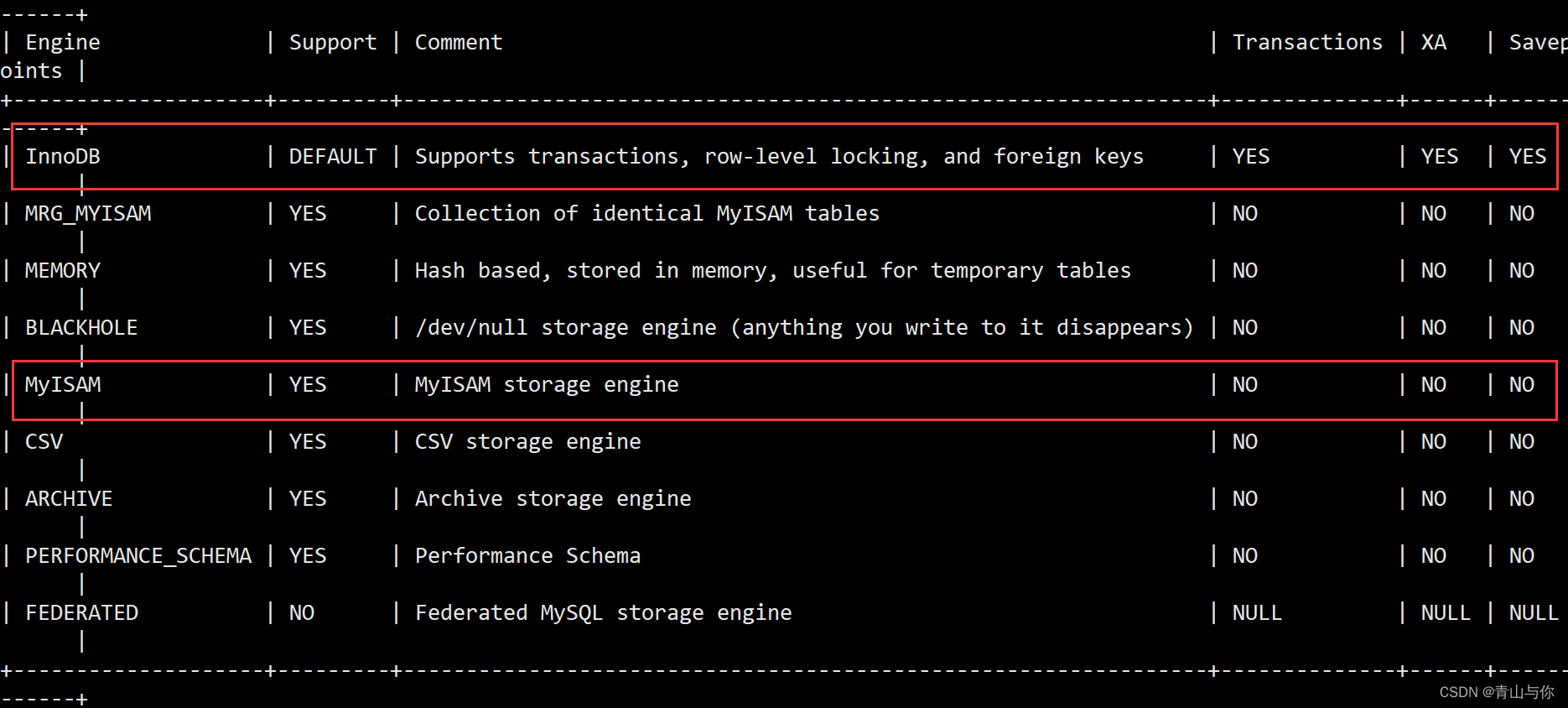
mysql基础概念
文章目录 登录mysqlmysql和mysqld数据库操作主流数据库MYSQL架构SQL分类 登录mysql 登录mysql连接服务器,mysql连接时可以指明主机用-h选项,然后就可以指定主机Ip地址,-P可以指定端口号 -u指定登录用户 -P指定登录密码 查看系统中有无mysql&…...
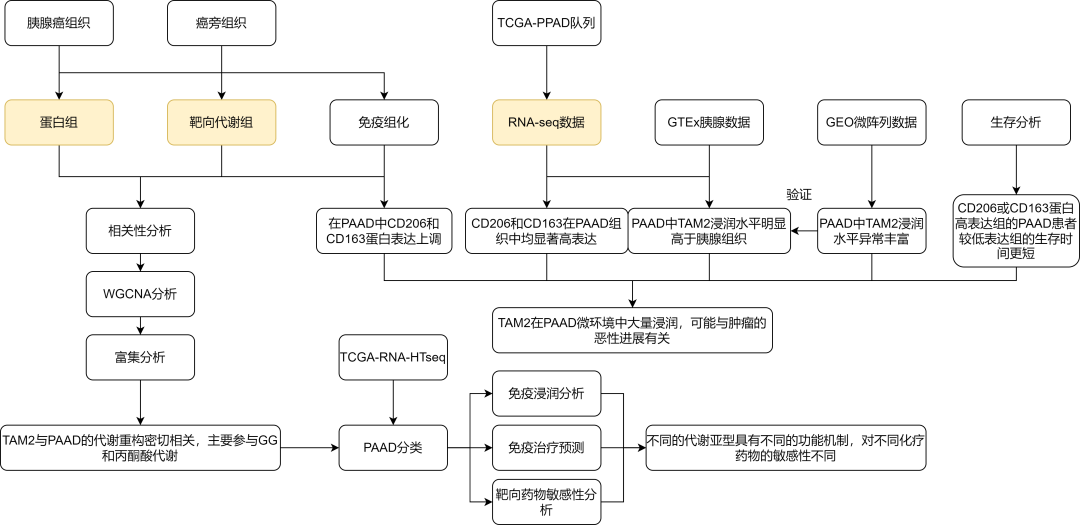
成功案例(IF=7.3)| 转录组+蛋白质组+代谢组联合分析分析揭示胰腺癌中TAM2相关的糖酵解和丙酮酸代谢重构
研究背景 肿瘤的进展和发展需要癌细胞的代谢重编程,癌细胞能量代谢模式的改变可以满足快速增殖和适应肿瘤微环境的需要。肿瘤微环境(TME)中的代谢状态受到多种因素的影响,包括血管生成、与其他细胞的相互作用和系统代谢。代谢异质…...

【C++ | 函数】默认参数、哑元参数、函数重载、内联函数
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 ⏰发布时间⏰:2024-05-04 1…...

Spring事件
📝个人主页:五敷有你 🔥系列专栏:Spring⛺️稳中求进,晒太阳 Spring事件 简洁 Spring Event(Application Event)就是一个观察者模式,一个bean处理完任务后希望通知其他Bean的…...
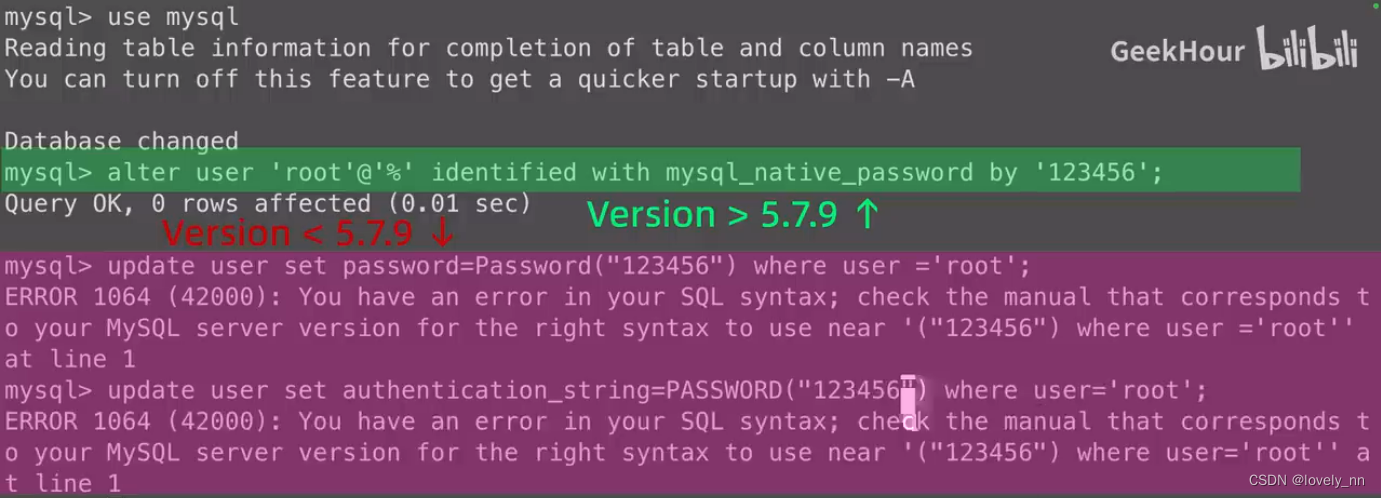
mysql安装及基础设置
关系型数据库 MySQL是一种关系型数据库管理系统,采用了关系模型来组织数据的数据库,关系数据库将数据保存在不同的表中,用户通过查询 sql 来检索数据库中的数据。 yum 方式安装 mysql # yum -y install mysql-server # systemctl start my…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
