图形网络的自适应扩散 笔记
1 Title
Adaptive Diffusion in Graph Neural Networks(Jialin Zhao、Yuxiao Dong、Ming Ding、Evgeny Kharlamov、Jie Tang)【NIPS 2021】
2 Conclusion
The neighborhood size in GDC is manually tuned for each graph by conducting grid search over the validation set, making its generalization practically limited. To address this issue,this study proposes the adaptive diffusion convolution (ADC)* strategy to automatically learn the optimal neighborhood size from the data. Furthermore, this paper breaks the conventional assumption that all GNN layers and feature channels (dimensions) should use the same neighborhood size for propagation.
3 Good Sentences
1、B oth strategies are limited to a pre-determined and fixed neighborhood for passing and receiving messages. Essentially, these methods have an implicit assumption that all graph datasets share the same size of receptive field during the message passing process.(The limitations of previous GCN methods)
2、To eliminate the manual search process of the optimal propagation neighborhood in GDC, we propose the adaptive diffusion convolution (ADC) strategy that supports learning the optimal neighborhood from the data automatically. ADC achieves this by formalizing the task as a bilevel optimization problem, enabling the customized learning of one optimal propagation neighborhood size for each dataset. In other words, all GNN layers and feature channels (dimensions) share the same neighborhood size during message passing on each graph.(The motivation of this study which can solve the problems GDC meets)
3、
为了消除GDC中最优传播邻域的人工搜索过程,我们提出了支持从数据中自动学习最优邻域的自适应扩散卷积(ADC)策略。ADC通过将任务形式化为一个双层优化问题来实现这一点,允许为每个数据集定制学习一个最优传播邻域大小。换句话说,所有GNN层和特征通道(维度)在每个图上传递消息时共享相同的邻域大小。
为了进一步实现这一目标,ADC能够从数据中自动学习每个GNN层和每个特征通道的自定义邻域大小。通过为每层学习唯一的传播邻域,ADC可以使gnn从不同的图结构中捕获邻居信息,这完全依赖于数据和下游学习目标。
同样,通过学习每个特征通道的不同邻域大小,gnn能够选择性地对每个邻居的多个特征信号进行建模。总之,ADC使gnn与图结构和所有特征通道完全耦合。
Neighborhood Radius in GNNs
本文研究了半监督节点分类问题。输入包括无向网络G = (V;E),其中节点集V包含n个节点,E为边集,A∈为图G的对称邻接矩阵。给定输入特征矩阵X和节点标签Y的一个子集,任务是预测剩余节点的标签。
Neighborhood Radius in Message Passing Networks:
在消息传递网络中,每个节点会收集来自其邻居节点的特征信息,并将这些信息聚合起来以更新自己的状态。消息传递网络可以简单定义为:![]()
这个过程通常在图神经网络的每一层中进行。"Neighborhood Radius" 指的是在消息传递过程中,一个节点能够聚合多远距离邻居的信息。其中,表示第
层的隐藏特征,
, X为输入特征的第1层隐藏特征,
(·)表示特征变换,γ(·)表示特征传播。
特征转换函数描述了特征如何在每个节点内部转换,特征传播函数描述了特征如何在节点之间传播。
![]()
![]()
![]() ,D为对角线上的元素是节点的度的矩阵
,D为对角线上的元素是节点的度的矩阵![]() ,
,表示变换后的隐特征,不过GCN使用带有自循环的邻接矩阵A。
大多数基于图的模型都可以表示![]()
=
![]() ,
,![]()
邻居半径r被定义为:![]() ,
,表示k个步距节点的影响。对于较大的r,这意味着模型更强调远距离节点,即全局信息。对于较小的r,这意味着模型放大了局部信息。对于GCN,邻域半径r = 1
Neighborhood Radius in Graph Diffusion Convolution
图扩散卷积(GDC)的传播解决了从离散跳数的特征传播到连续图扩散的推广问题: ,k从0到无穷求和,使得每个节点都聚集了整个图的信息。而权重系数满足
,k从0到无穷求和,使得每个节点都聚集了整个图的信息。而权重系数满足![]() ,这样在传播过程中信号强度不会被放大或减弱。论文原句:In this work, we focus on heat kernel,也就是说作者令
,这样在传播过程中信号强度不会被放大或减弱。论文原句:In this work, we focus on heat kernel,也就是说作者令![]()
HK:热核将先验知识引入到GNN模型中,这意味着特征在节点之间的传播遵循牛顿冷却定律,即两个节点之间的特征传播速度与它们之间的特征差成正比。在形式上,这种先验知识可以描述为:
其中N(i)表示节点i的邻域,表示节点i在扩散时间t后的特征。微分方程可解为:
![]() ,X(t)为扩散时间t后的特征矩阵,
,X(t)为扩散时间t后的特征矩阵,![]() 是热核
是热核
Neighborhood radius  in diffusion models
in diffusion models
根据邻域半径的定义,GDC的热核版本邻域半径的定义为:

这表明t是基于热核的GDC的邻域半径,即t成为多跳数模型中跳数(hop-number)的完美连续替代。
Adaptive Diffusion Convolution
其中,拉普拉斯矩阵,对于每个图数据集,需要手动网格搜索步骤来确定与邻域半径相关的参数t,此外,对于每个数据集中的所有特征通道和传播层,t是固定的。
Training Neighborhood Radius
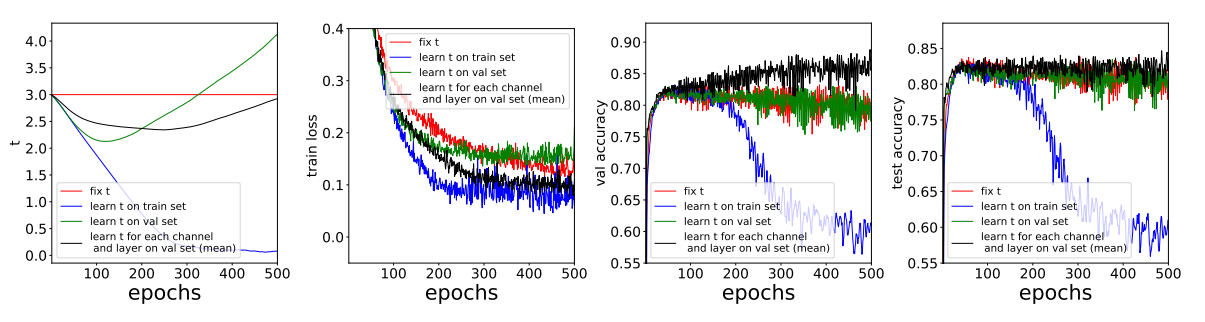
上图显示了学习t的训练过程。随着epoch的增加,在训练集(蓝色)上学习时,t和训练损失都减小。同时,验证和测试精度急剧下降,因为t趋于零(更多的epoch) -表示每个节点只能使用自己的特征来预测标签, 也就是说,直接在训练集上学习t会导致过拟合。
为了解决这个问题,本文提出了一种通过在验证集上使用模型的梯度来训练t的方法。该模型的目标是找到使验证损失![]() ,其中w表示特征变换函数中所有其他可训练参数,w *表示使训练损失
,其中w表示特征变换函数中所有其他可训练参数,w *表示使训练损失![]() 。该策略可以形式化为一个双层优化问题
。该策略可以形式化为一个双层优化问题
如果按上面的方法,每次更新t时,需要使w收敛到最优值,这就太贵了。一种近似方法是每次更新w时更新t,也就是说,![]()
![]() ,其中,e表示训练epoch的个数,α1和α2分别表示训练集和验证集的学习率。
,其中,e表示训练epoch的个数,α1和α2分别表示训练集和验证集的学习率。
Training Neighborhood Radius for Each Layer and Channel:
对于GDC, 一个数据集有一个邻域半径t,即所有GNN层和所有特征通道(维度)都有相同的t。先前模型无法实现这一目标的障碍在于,考虑到随着参数数量的增加,时间复杂度呈指数增长,对每个特征通道和GNN层的传播函数分别进行手动调整或网格搜索是不可行的挑战。然而,前面提到的在模型训练过程中更新t的策略使得ADC能够自适应地学习所有层和所有特征通道的特定t。本文通过将特征传播函数扩展到每个层和通道,即从t到,得到自适应扩散卷积(ADC),
 ,其中
,其中表示第
层和第
通道的邻域半径t,
表示隐藏特征
的第
列,即通道
上的特征,
![]() 表示第
表示第层和第
通道上的特征传播函数.

Generalized adaptive diffusion convolution (GADC):
在不损失一般性的情况下,可以将ADC扩展为广义ADC (GADC),即不将权系数θk限制为热核。因此,得到GADC的特征传播为:

式中,表示第
层和第
通道上
跳邻居的权系数。
Results
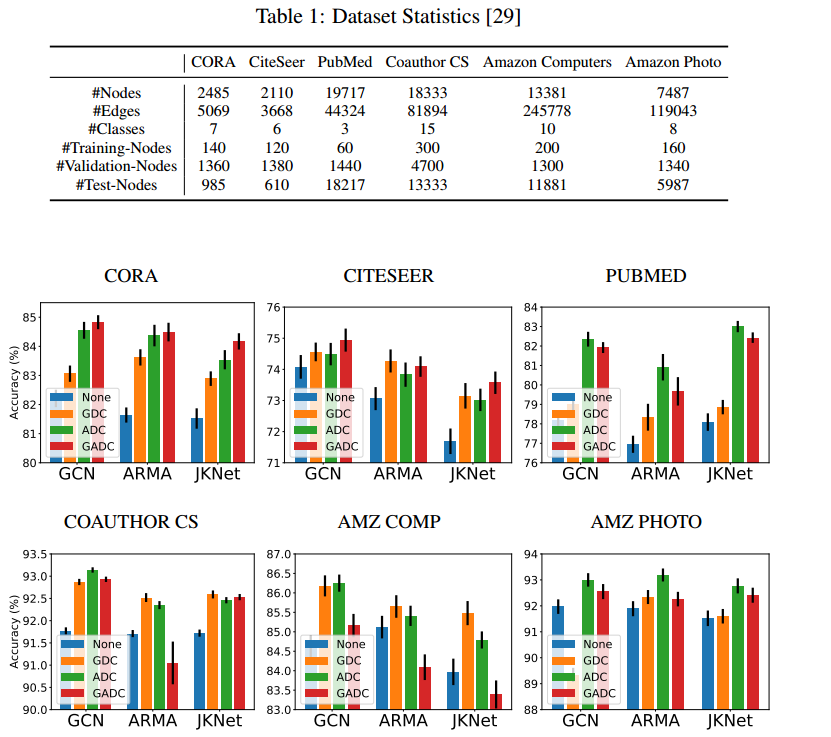
相关文章:

图形网络的自适应扩散 笔记
1 Title Adaptive Diffusion in Graph Neural Networks(Jialin Zhao、Yuxiao Dong、Ming Ding、Evgeny Kharlamov、Jie Tang)【NIPS 2021】 2 Conclusion The neighborhood size in GDC is manually tuned for each graph by conductin…...

vue基础配置
vite.config.ts import { defineConfig } from vite import vue from vitejs/plugin-vue import path from "path"; //引入svg需要用到的插件 import { createSvgIconsPlugin } from vite-plugin-svg-icons //mock插件提供方法 import { viteMockServe } from vite-…...
C++基础中的存储类别
存储的类别是变量的属性之一,C语言定义了4种变量的存储类别,分别是auto变量、static变量、register变量和extern变量。以下重点介绍这几种类型。 一、auto变量 auto变量是C默认的存储类型。函数内未加存储类型说明的变量均被称为自动变量,即…...
【NPM】Nginx Proxy Manager 一键申请 SSL 证书,自动续期,解决阿里云SSL免费证书每3个月失效问题
文章目录 1、NPM 简介2、实战Step 1:环境搭建 也可以看作者安装笔记 Step 2:创建容器 2.1 在系统任意位置创建一个文件夹,此文档以~/nginx-proxy-manager为例。2.2 创建docker-compose.yaml2.3 启动NPM服务 Step 3:配置反向代理3…...
教你解决PUBG绝地求生游戏中闪退掉线无法重连回去的问题
《绝地求生》(PUBG),作为一款在全球范围内掀起热潮的战术竞技游戏,以其栩栩如生的战场环境和令人心跳加速的生存冒险博得了广大玩家的青睐。然而,一些玩家在经历了一场惊心动魄的对局后,却面临了一个不大不…...
LAMP+phpMyAdmin部署)
24 Debian如何配置Apache2(4)LAMP+phpMyAdmin部署
作者:网络傅老师 特别提示:未经作者允许,不得转载任何内容。违者必究! Debian如何配置Apache2(4)LAMP+phpMyAdmin部署 《傅老师Debian小知识库系列之24》——原创 ==前言== 傅老师Debian小知识库特点: 1、最小化拆解Debian实用技能; 2、所有操作在VM虚拟机实测完成;…...

centos安装paddlespeech各种报错解决方案
背景 windows系统安装paddlespeech一路顺利 centos安装之前也是正常 今天centos再次安装各种报错,避免以后遇到浪费时间,记录下来,也给大家节约时间 报错 报错1 module numpy has no attribute complex. 解决方案 降低numpy # 1. 卸载当前numpy库 pip uninstall numpy…...

谈基于ATTCK框架的攻击链溯源
引言 网络安全在当今数字化时代变得尤为关键,而MITRE公司开发的ATT&CK框架则成为了安全专业人员的重要工具。ATT&CK是一种广泛使用的攻击行为分类和描述框架。其目的在于提供一个共同的语言,使安全专业人员能够更好地理解攻击者的行为和目标&…...

在Ubuntu下搭建自己的以太坊私有链
最近要对链及链上应用进行压测,为了方便操作及分析问题,就自己搭建了一个eth私链。当前版本安装官方指引发现有卡点,于是决定整理一个文档,为其他有需要的朋友提供便捷操作,节约时间。 一、环境配置 linux操作系统:Ubuntu 20.04.6 LTS (Focal Fossa) go version: go1…...

巩固学习4
python中函数逆置的几种方法 s input()for i in range(len(s)-1,-1,-1):#从最后一位开始,步长为-1print(s[i],end)用for语句循环逆置 s input() s list(s) n len(s) for i in range(n//2):s[i],s[n-1-i] s[n-1-i],s[i]#从中间反转字符串 res "".j…...

Conda安装rasterio报错
Conda安装rasterio报错 文章目录 Conda安装rasterio报错问题解决参考 问题 在conda环境中安装rasterio包之后,本来可以正常运行的,但是之后又重新安装了一个gdal,导致原来的引用rasterio的包的程序不可正常运行了 conda install rasterio c…...
linux安装 mysql
环境:centOS8 一、安装 1 安装wget库 sudo yum -y install wget 2. 安装 mysql 换yum源 亲测成功!!!!!! 换yum源 1.下载对应版本的repo文件 wget -O CentOS-Base.repo http://mirrors…...
暴力法解决最近对问题和凸包问题-实现可视化
目录 最近对问题 凸包问题 最近对问题 顾名思义就是采用蛮力法求出所有点之间的距离,然后进行比较找出第一个最近对,一个一个进行比较。 大概思路就是如图(每个圈代表一个数对) 第一个和其他四个比较 第二个和其他三个比较 …...
[Kubernetes] Rancher 2.7.5 部署 k8s
server: 192.168.66.100 master: 192.168.66.101 node1: 192.168.66.102 文章目录 1.rancher server 安装docker2.部署k8s3.kubeconfig4.测试集群 1.rancher server 安装docker 所有主机开通ipv4 vi /etc/sysctl.conf#加入 net.ipv4.ip_forward 1#配置生效 sysctl -prancher…...
码题杯 世界警察 思想:双指针
https://www.matiji.net/exam/brushquestion/4/4446/16A92C42378232DEB56179D9C70DC45C 双指针 思路是这样的,首先r指针向右走,如果r指针遇到了和l指针一样的,那么l指针就,一直加到r指针的位置,此时a[l]a[r]࿰…...
drawio 网页版二次开发(1):源码下载和环境搭建
目录 一 说明 二 源码地址以及下载 三 开发环境搭建 1. 前端工程地址 2. 配置开发环境 (1)安装 node.js (2)安装 serve 服务器 3. 运行 四 最后 一 说明 应公司项目要求,需要对drawio进行二次开发&…...

算法训练Day33 |● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
509. 斐波那契数 class Solution { public:int fib(int n) {if(n<1) return n;int pre2 0;int pre1 1;int result 0;for(int i2; i<n; i ){result pre1pre2;pre2 pre1;pre1 result;}return result;} };参考文章:代码随想录- 509. 斐波那契数 70. 爬楼梯…...
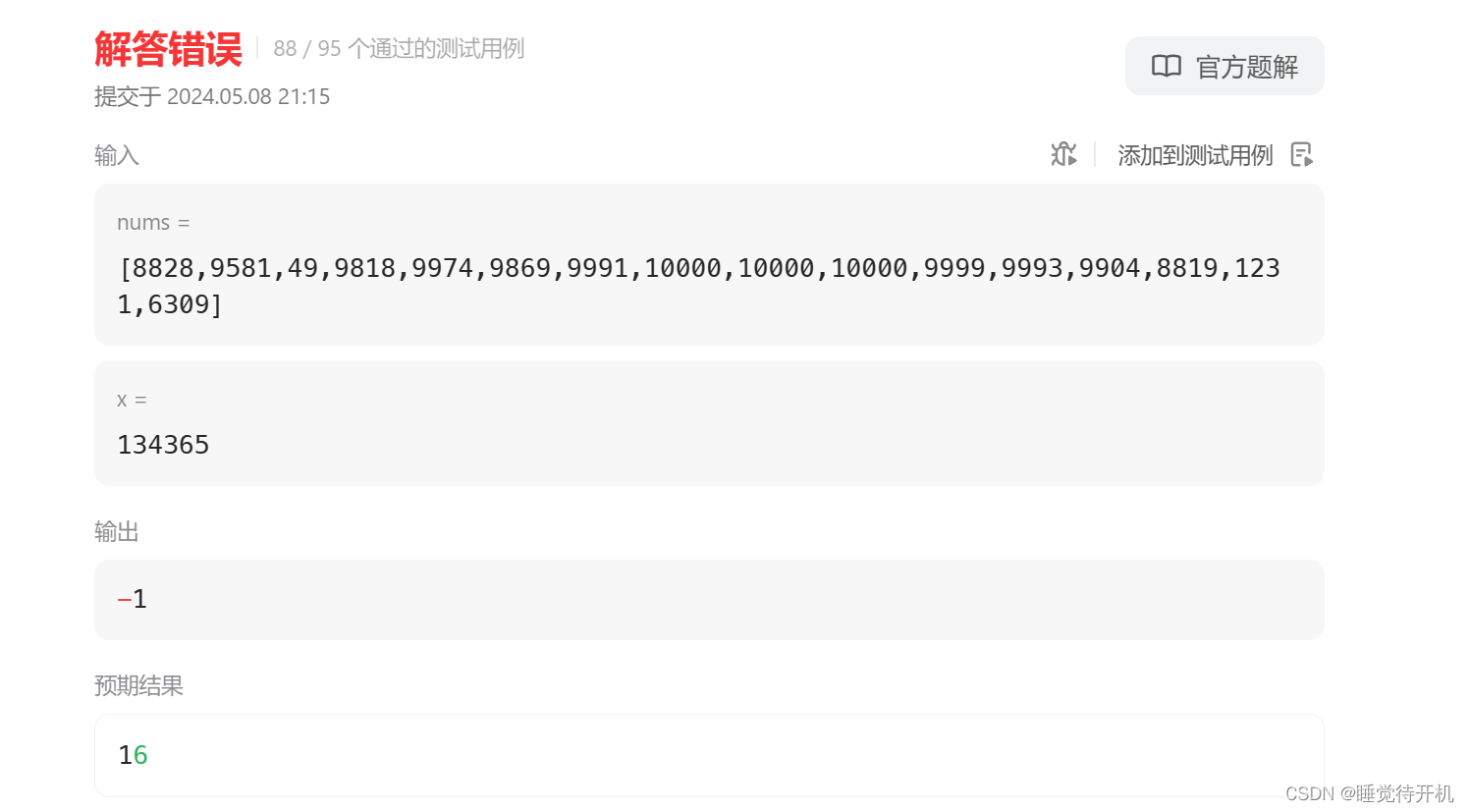
【算法】滑动窗口——将x减到0的最小操作数
本节博客主要是讲的我解“将x减到0的最小操作数”这道题的思路历程,从最开始的想法到代码提交的详细记录,有需要借鉴即可。 目录 1.题目2.代码示例3.细节3.1left越界3.2特殊情况 4.总结 1.题目 题目链接:LINK 看题目意思是就是给你一个数X&…...

《引爆流量获客技术》实操方法,手把手教你搭建盈利流量池
[1]-先导课.mp4 [2]-第1节:设计客户终身价值的方法和买客户思维.mp4 [3]-第2节:【渠道模型】解决谁是我的客户如何找到.mp4 [4]-第3节:【诱饵模型】解决 如何获得更多的客户.mp4 [5]-第4节:【钩子模型】解决让目标客户主动找你…...
【记录】常见的前端设计系统(Design System)
解释一下设计系统的定义,以及在国内,都有那些优秀的设计系统可以学习,希望可以帮到大家。 什么是设计系统(Design System)? 设计系统(Design System)是一套综合性的指导原则、组件和规则&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
