当前位置： 首页 > news >正文

每天五分钟深度学习：数学中的极值

news 2026/2/8 5:49:50

本文重点

在数学领域中，极值是一个极其重要的概念，它不仅在纯数学理论研究中占据核心地位，而且在工程、物理、经济等实际应用领域也发挥着不可替代的作用。极值问题涉及函数的最大值和最小值，是微积分学中的一个基本问题。本文旨在详细介绍数学中的极值概念、性质、求解方法以及其在各个领域的应用。

极值的定义与性质

极值的定义

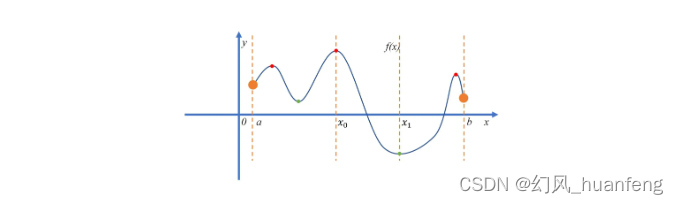
极值是指函数在某一区间内，当自变量取某一特定值时，函数值达到最大或最小。具体来说，如果函数f(x)在x=c处的函数值大于或等于其邻近的所有值，则称f(c)是函数f(x)的局部最大值；如果函数f(x)在x=c处的函数值小于或等于其邻近的所有值，则称f(c)是函数f(x)的局部最小值。如果在整个定义域内，f(c)都是最大的或最小的，则称f(c)是函数f(x)的全局最大值或全局最小值。

极值的性质

极值具有以下基本性质：

（1）极值点处的一阶导数等于零（或不存在）。这是因为如果函数在某点处可导且取得极值，则该点处的一阶导数必须为零。然而，一阶导数等于零的点并不一定是极值点，也可能是拐点或其他类型的点。

（2）极值点处的二阶导数可以用来判断极值的类型。如果函数在某点处二阶导数大于零，则该点是局部最小值；如果二阶导数小于零，则该点是局部最大值。这一性质在求解极值问题时非常有用。

极值问题

相关文章：

每天五分钟深度学习：数学中的极值

本文重点 在数学领域中，极值是一个极其重要的概念，它不仅在纯数学理论研究中占据核心地位，而且在工程、物理、经济等实际应用领域也发挥着不可替代的作用。极值问题涉及函数的最大值和最小值，是微积分学中的一个基本问题。本文旨在详细介绍数学中的极值概念、性质、求解方…...

编程日记 2024/5/10 23:27:44

【Linux】Linux——Centos7安装Tomcat

1.下载Tomcat 安装包 官网地址：Apache Tomcat - Apache Tomcat 9 Software Downloadshttps://tomcat.apache.org/download-90.cgi 2.将下载的安装包上传到 Xftp 上，我是直接放到 usr 下了 3.将安装包解压到 /usr/local/ tar -zxvf apache-tomcat-9.0.8…...

编程日记 2024/5/10 23:26:43

SpringBoot+vue实现右侧登录昵称展示

目录 1. 定义User数据 1.1.在created方法获取数据 1.2.头部导航栏绑定User数据 1.3.在data中定义User数据 2. 获取数据 2.1.接收父组件传递的值 2.2.展示数据 3. 页面效果 在SpringBoot和 Vue.js 结合的项目中实现右侧登录昵称展示，通常涉及到前端的用户界面…...

编程日记 2024/5/10 23:25:41

【网络原理】UDP协议 | UDP报文格式 | 校验和 | UDP的特点 | 应用层的自定义格式

文章目录 一、UDP协议1.UDP的传输流程发送方接收方 2.UDP协议报文格式：长度受限校验和如何校验：CRC算法：循环冗余算法md5算法： 2.UDP的特点 二、开发中常见的自定义格式1.xml（古老）2.json（最流行…...

编程日记 2024/5/10 23:24:40

NodeJs入门知识

**************************************************************************************************************************************************************************** 1、配置Node.js与npm下载（精力所致，必有精品） …...

编程日记 2024/5/10 23:22:37

代码随想录学习Day 34

62.不同路径 题目链接 讲解链接 动归五部曲： 1.确定dp数组及其下标的含义：dp[i][j]的含义是从(0, 0)走到(i, j)所需的步数； 2.确定递推公式：因为只能往右或者往下，所以dp[i][j] dp[i - 1][j] dp[i][j - 1]。 3.…...

编程日记 2024/5/10 23:20:35

由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题

由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题 一、问题详细描述二、问题产生背景三、问题原因四、解决办法1、安装缺少的库2、直接更换更高版本的opencv 五、vs版本对应vc1、版本对应2、vs对应vc查看方法 一、问题详细描述 同样可能会报 &#xff…...

编程日记 2024/5/10 23:18:30

【前端】输入时字符跳动动画实现

输入时字符跳动动画实现 在前端开发中，为了提升用户体验，我们经常需要为用户的交互行为提供即时的反馈。这不仅让用户知道他们的操作有了响应，还可以让整个界面看起来更加生动、有趣。本文将通过一个简单的例子讲解如何实现在用户输入字符时…...

编程日记 2024/5/10 23:17:29

C语言面试重点问题

1. 冒泡排序法 2. strlen、strcpy、strcat、strcmp的用法和原理 3. 大小端的区分 3.1 主函数区分大小端 #include <stdio.h>int main(void) {int num 0x11223344;char *p (char *)&num;if (0x11 *p){printf("大端!\n");}else if (0x44 *p){printf(…...

编程日记 2024/5/10 23:16:27

antlr4略解

文章目录 1. antlr4是用来干什么的&#xff1f;2. 什么是lexer和parser&#xff1f;3. 使用antlr4生成某语言的lexer和parser的具体过程4. 其他 1. antlr4是用来干什么的&#xff1f; 是用来生成某语言lexer和parser的。 通俗点说&#xff0c;就是输入一个语言的规则描述文件&…...

编程日记 2024/5/10 23:15:26

超级好用的C++实用库之文件目录操作

&#x1f4a1; 需要该C实用库源码的大佬们&#xff0c;可扫码关注文章末尾的微信公众号二维码&#xff0c;或搜索微信公众号“希望睿智”。添加关注后&#xff0c;输入消息“超级好用的C实用库”&#xff0c;即可获得源码的下载链接。 概述 文件和目录操作是操作系统层面上的基…...

编程日记 2024/5/10 23:13:23

结合kimi chat的爬虫实战思路

背景 想钻研一下项目组件&#xff0c;找找之后的学习方向。不能自以为是&#xff0c;所以借着网开源项目网站上公布的项目内容看一下&#xff0c;那些是我可以努力去学习的&#xff08;入门的&#xff09;。首先需要获取相关内容&#xff0c;于是爬取整理。 任务1&#xff1a…...

编程日记 2024/5/10 23:12:22

UnsupportedClassVersionError异常如何解决？

下面是异常报错的详细描述 java -version java version "17.0.11" 2024-04-16 LTS Java(TM) SE Runtime Environment (build 17.0.117-LTS-207) Java HotSpot(TM) 64-Bit Server VM (build 17.0.117-LTS-207, mixed mode, sharing) 环境变量已经是jdk17&#xff0c;但…...

编程日记 2024/5/10 23:11:20

LeetCode热题100｜动态规划Part.1｜70.爬楼梯、118.杨辉三角、198.打家劫舍

70.爬楼梯 代码随想录原题&#xff0c;看这篇文章&#xff1a;C动态规划Part.1|动态规划理论基础、509.斐波那契数、70.爬楼梯、746.使用最小花费爬楼梯 118.杨辉三角 题目链接&#xff1a;118.杨辉三角 一刷代码 时间复杂度和空间复杂度都造到 O ( n u m R o w s 2 ) O(num…...

编程日记 2024/5/10 23:10:19

python 根据网址和关键词批量下载影像

最近用到了GLASS的LAI产品&#xff0c;但这个产品的文件夹分得很细&#xff0c;我需要的影像又有8个瓦片&#xff0c;一个一个点击很麻烦&#xff0c;于是探索了批量下载的方法 一、下载1幅 import requests import re import os import requests import re# 网页URLurl &…...

编程日记 2024/5/10 23:06:15

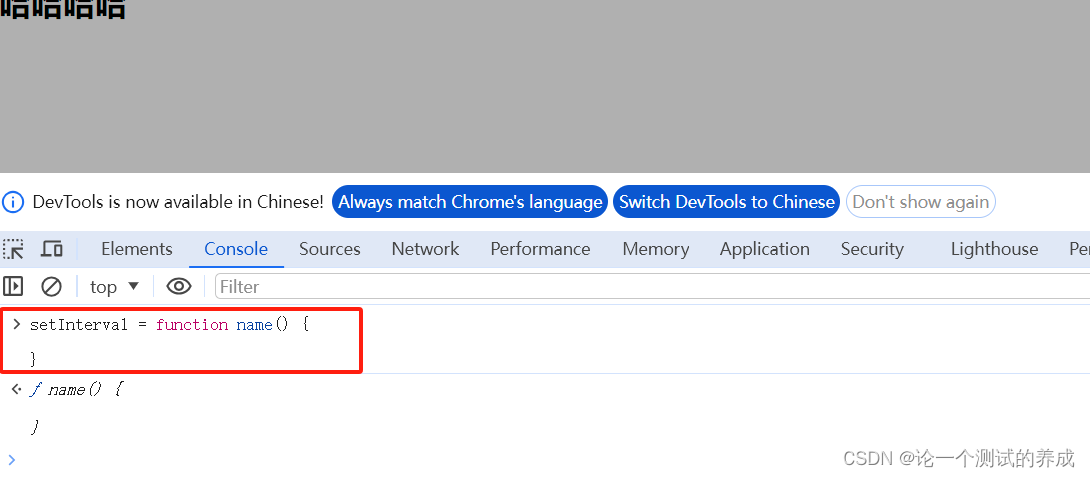
爬虫-无限debug场景 解决方式

解决无限debug 场景1 1. 鼠标右键 选择 continue to here&#xff08;此处不停留&#xff09;2. 鼠标右键 选择 edite breakpoint 设置 10 保证条件不成立 这行永远不执行3.方法置空 1. 方法调用加断点2. 控制台 setInterval function name() {}4. 替换文件 5. hoo…...

编程日记 2024/5/10 23:04:13

[链表专题]力扣206, 203, 19

1. 力扣206 : 反转链表 (1). 题 : 图略 给你单链表的头节点 head &#xff0c;请你反转链表&#xff0c;并返回反转后的链表。示例 1&#xff1a;输入&#xff1a;head [1,2,3,4,5] 输出&#xff1a;[5,4,3,2,1] 示例 2&#xff1a;输入&#xff1a;head [1,2] 输出&#x…...

编程日记 2024/5/10 23:03:11

秋招后端开发面试题 - MySQL基础

目录 MySQL基础前言面试题MySQL 基础篇Mysql 的基础架构&#xff1f;MySQL 的长连接和短连接长连接引起的异常重启问题&#xff1f;说一下 MySQL 执行一条查询语句的内部执行过程&#xff1f;MySQL 查询缓存的功能有何优缺点&#xff1f;MySQL 的常用引擎都有哪些&#xff1f;I…...

编程日记 2024/5/10 23:01:09

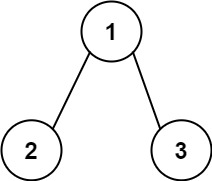
力扣每日一题113：路径总和||

题目 中等 给你二叉树的根节点 root 和一个整数目标和 targetSum &#xff0c;找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节点 是指没有子节点的节点。 示例 1&#xff1a; 输入&#xff1a;root [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSu…...

编程日记 2024/5/10 23:00:07

Thinkphp5 中常见的session 操作方法

在 ThinkPHP 框架中&#xff0c;session 是用于在多个页面或请求之间存储用户信息的机制。以下是在 ThinkPHP 中进行 session 常见操作的一些示例&#xff1a; 启动 Session 在 ThinkPHP 中&#xff0c;通常不需要手动启动 Session&#xff0c;因为框架会在应用启动时自动处理…...

编程日记 2024/5/10 22:57:04

国防科技大学计算机基础课程笔记02信息编码

1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制&#xff0c;因此这个了16进制的数据既可以翻译成为这个机器码&#xff0c;也可以翻译成为这个国标码&#xff0c;所以这个时候很容易会出现这个歧义的情况&#xff1b; 因此&#xff0c;我们的这个国…...

编程新知 2026/2/8 4:37:15

Golang 面试经典题：map 的 key 可以是什么类型？哪些不可以？

Golang 面试经典题&#xff1a;map 的 key 可以是什么类型&#xff1f;哪些不可以&#xff1f; 在 Golang 的面试中&#xff0c;map 类型的使用是一个常见的考点&#xff0c;其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

编程新知 2025/12/20 7:42:02

Xshell远程连接Kali（默认 | 私钥）Note版

前言:xshell远程连接&#xff0c;私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

编程新知 2026/1/28 2:18:42

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2026/1/31 6:04:01

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2026/2/4 15:29:40

全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比

目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec&#xff1f; IPsec VPN 5.1 IPsec传输模式&#xff08;Transport Mode&#xff09; 5.2 IPsec隧道模式&#xff08;Tunne…...

编程新知 2025/11/3 0:44:41

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/2/6 1:04:23

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制

使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下&#xff0c;限制某个 IP 的访问频率是非常重要的&#xff0c;可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案&#xff0c;使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

编程新知 2025/10/22 6:06:44

腾讯云V3签名

想要接入腾讯云的Api&#xff0c;必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口&#xff0c;但总是卡在签名这一步&#xff0c;最后放弃选择SDK&#xff0c;这次终于自己代码实现。 可能腾讯云翻新了接口文档&#xff0c;现在阅读起来&#xff0c;清晰了很多&…...

编程新知 2026/1/24 4:39:04