element ui的table多选
使用el-table的selection-change事件来获取选中的值;
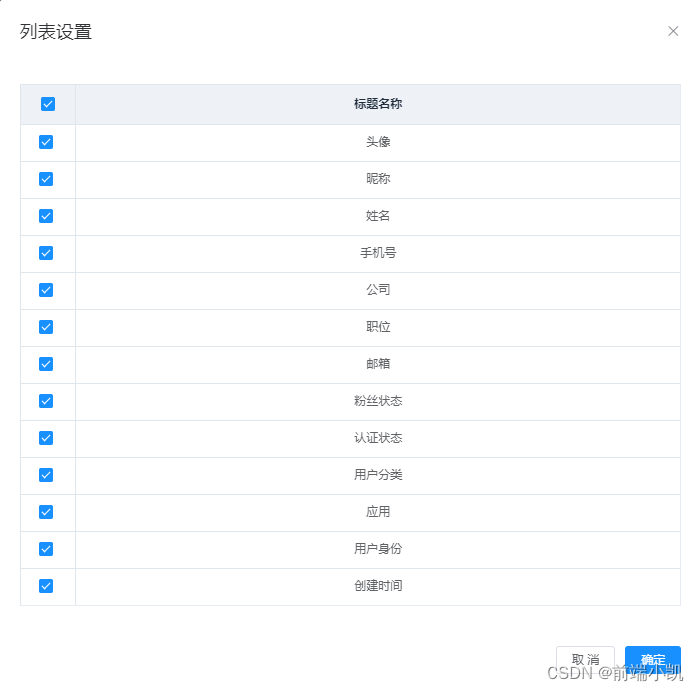
例:
html代码:
<el-button type="primary" @click="openTableSet">列表设置</el-button><!-- 列表设置弹框 -->
<el-dialog :close-on-click-modal="false" title="列表设置" :visible.sync="tableSetShow" append-to-body><el-table ref="tableSet" :data="tableSetData" border style="width: 100%" :cell-style="{ textAlign: 'center' }" header-cell-class-name="table-th" @selection-change="tableSetMultipleChange" v-if="tableSetShow"><el-table-column type="selection" width="55"></el-table-column><el-table-column prop="title" label="标题名称" /></el-table><div slot="footer" class="dialog-footer"><el-button @click="tableSetShow = false">取 消</el-button><el-button type="primary" @click="editTableSetMultiple">确定</el-button></div>
</el-dialog>js变量代码:
// 列表设置显示隐藏
tableSetShow: false,
// 列表设置数据
tableSetData: [{ key: "avatar", title: "头像"},{ key: "nickname", title: "昵称"},{ key: "name", title: "姓名"},{ key: "mobile", title: "手机号"},{ key: "company", title: "公司"},{ key: "position", title: "职位"},{ key: "email", title: "邮箱"},{ key: "subscribe", title: "粉丝状态"},{ key: "authorized", title: "认证状态"},{ key: "type", title: "用户分类"},{ key: "app", title: "应用"},{ key: "identity", title: "用户身份"},{ key: "created_at", title: "创建时间"}
],
// 列表设置多选数据
tableSetMultiple: [],
// 列表绑定多选值判断显示隐藏
tableSetMultipleBinding: []js方法代码:
/*** 打开列表设置*/
openTableSet() {this.tableSetShow = true;this.getTableSetMultiple();
},
/*** 列表设置列表多选改变*/
tableSetMultipleChange(val) {this.tableSetMultiple = [];val.forEach(item => {this.tableSetMultiple.push(item.key);});
},
/*** 列表设置获取数据*/
async getTableSetMultiple() {let params = {list_name: "user"};let res = await getTableColumnData(params);if (res.code == 200) {let data = res.data.json_data;if (data.length == 0) data = ["avatar", "nickname", "name", "mobile", "company", "position", "email","subscribe", "authorized", "type", "app", "identity", "created_at"];this.tableSetMultiple = [];this.tableSetMultipleBinding = [];this.$nextTick(() => {this.tableSetData.forEach(item => {data.forEach(item2 => {if (item.key == item2) {this.tableSetMultiple.push(item.key);this.tableSetMultipleBinding.push(item.key);this.$refs.tableSet ? this.$refs.tableSet.toggleRowSelection(item) : "";};});});});};
},
/*** 列表设置保存数据*/async editTableSetMultiple() {if (this.tableSetMultiple.length == 0) {this.$message.warning("请最少选择一项展示");return false;};let params = {list_name: "user",json_data: this.tableSetMultiple};let res = await updateTableColumnData(params);if (res.code == 200) {this.getTableSetMultiple();this.tableSetShow = false;this.$message.success("保存成功");} else {this.$message.error("保存失败");}
}相关文章:

element ui的table多选
使用el-table的selection-change事件来获取选中的值; 例: html代码: <el-button type"primary" click"openTableSet">列表设置</el-button><!-- 列表设置弹框 --> <el-dialog :close-on-click-mo…...

python基础---基础运算
基础运算 可以使用type获取一个变量的类型 常见的数据类型 整形, 可以存储任意大小的整数, 支持二进制(如0b100,换算成十进制是4)、八进制(如0o100,换算成十进制是64)、十进制(100)…...
【数学】泰勒公式
目录 引言 一、泰勒公式 1.泰勒公式及推导 (1)推导 (2)公式 2.泰勒中值定理 (1)定理1(佩亚诺余项) (2)定理2(拉格朗日余项) …...

C++基础-编程练习题及答案
文章目录 前言一、查找“支撑数”二、数组元素的查找三、爬楼梯四、数字交换五、找高于平均分的人 前言 C基础-编程练习题和答案 一、查找“支撑数” 【试题描述】 在已知一组整数中, 有这样一种数非常怪, 它们不在第一个, 也不在最后一个&…...
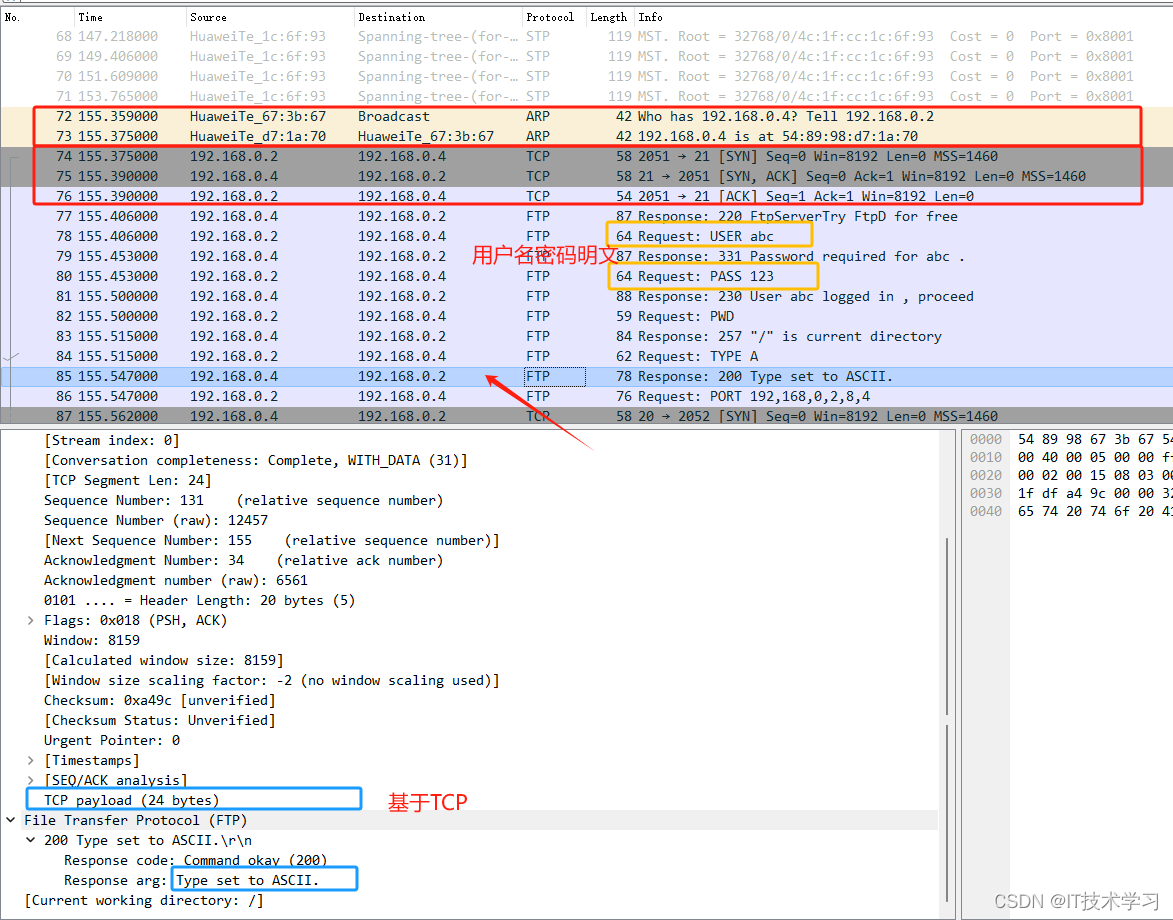
eNSP-抓包解析HTTP、FTP、DNS协议
一、环境搭建 1.http服务器搭建 2.FTP服务器搭建 3.DNS服务器搭建 二、抓包 三、http协议 1.HTTP协议,建立在TCP协议之上 2.http请求 3.http响应 请求响应报文参考:https://it-chengzi.blog.csdn.net/article/details/113809803 4.浏览器开发者工具抓包…...
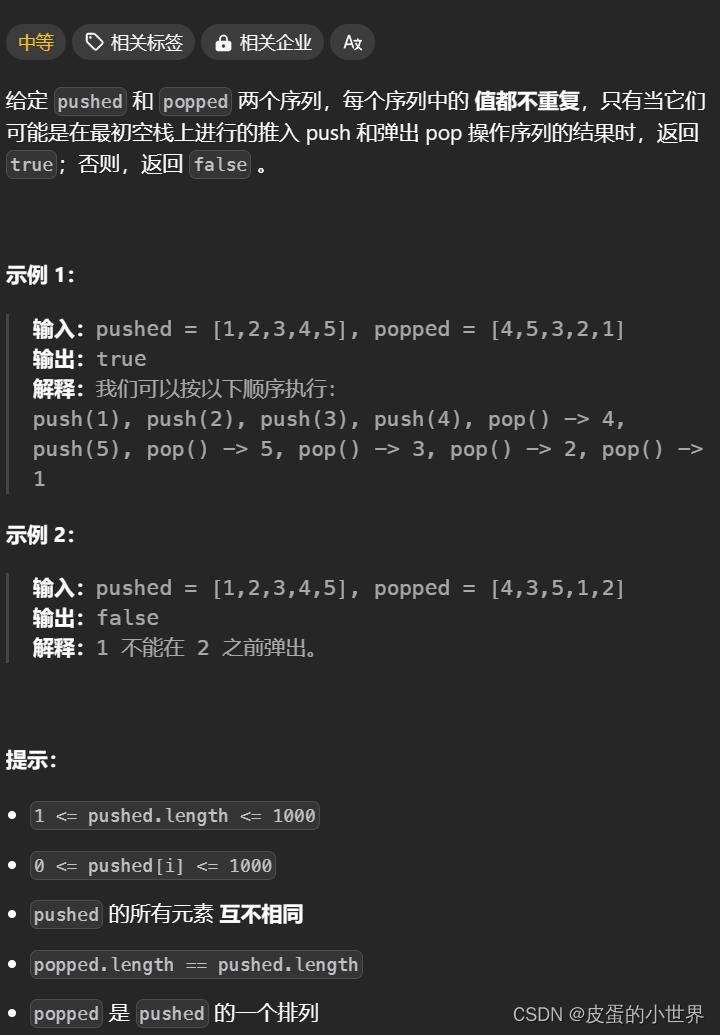
【栈】Leetcode 验证栈序列
题目讲解 946. 验证栈序列 算法讲解 在这里就只需要模拟一下这个栈的出栈顺序即可:使用一个stack,每次让pushed里面的元素入栈,如果当前栈顶的元素等于poped容器中的当前元素,因此就需要让栈顶元素出栈,poped的遍历…...
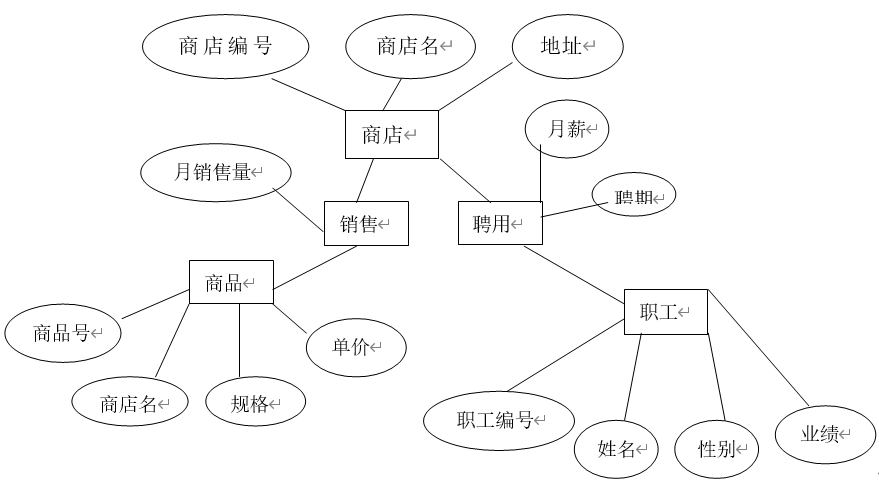
【数据库原理及应用】期末复习汇总高校期末真题试卷08
试卷 一、选择题(每题 2 分,共 30 分) 1. ___ ____是长期存储在计算机内的有组织,可共享的数据集合. A.数据库管理系统 B.数据库系统 C.数据库 D.文件组织 2. 数据库类型是按照 来划分…...
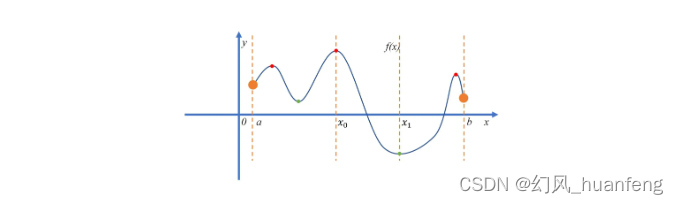
每天五分钟深度学习:数学中的极值
本文重点 在数学领域中,极值是一个极其重要的概念,它不仅在纯数学理论研究中占据核心地位,而且在工程、物理、经济等实际应用领域也发挥着不可替代的作用。极值问题涉及函数的最大值和最小值,是微积分学中的一个基本问题。本文旨在详细介绍数学中的极值概念、性质、求解方…...

【Linux】Linux——Centos7安装Tomcat
1.下载Tomcat 安装包 官网地址:Apache Tomcat - Apache Tomcat 9 Software Downloadshttps://tomcat.apache.org/download-90.cgi 2.将下载的安装包上传到 Xftp 上,我是直接放到 usr 下了 3.将安装包解压到 /usr/local/ tar -zxvf apache-tomcat-9.0.8…...

SpringBoot+vue实现右侧登录昵称展示
目录 1. 定义User数据 1.1.在created方法获取数据 1.2.头部导航栏绑定User数据 1.3.在data中定义User数据 2. 获取数据 2.1.接收父组件传递的值 2.2.展示数据 3. 页面效果 在SpringBoot和 Vue.js 结合的项目中实现右侧登录昵称展示,通常涉及到前端的用户界面…...

【网络原理】UDP协议 | UDP报文格式 | 校验和 | UDP的特点 | 应用层的自定义格式
文章目录 一、UDP协议1.UDP的传输流程发送方接收方 2.UDP协议报文格式:长度受限校验和如何校验:CRC算法:循环冗余算法md5算法: 2.UDP的特点 二、开发中常见的自定义格式1.xml(古老)2.json(最流行…...

NodeJs入门知识
**************************************************************************************************************************************************************************** 1、配置Node.js与npm下载(精力所致,必有精品) …...

代码随想录学习Day 34
62.不同路径 题目链接 讲解链接 动归五部曲: 1.确定dp数组及其下标的含义:dp[i][j]的含义是从(0, 0)走到(i, j)所需的步数; 2.确定递推公式:因为只能往右或者往下,所以dp[i][j] dp[i - 1][j] dp[i][j - 1]。 3.…...
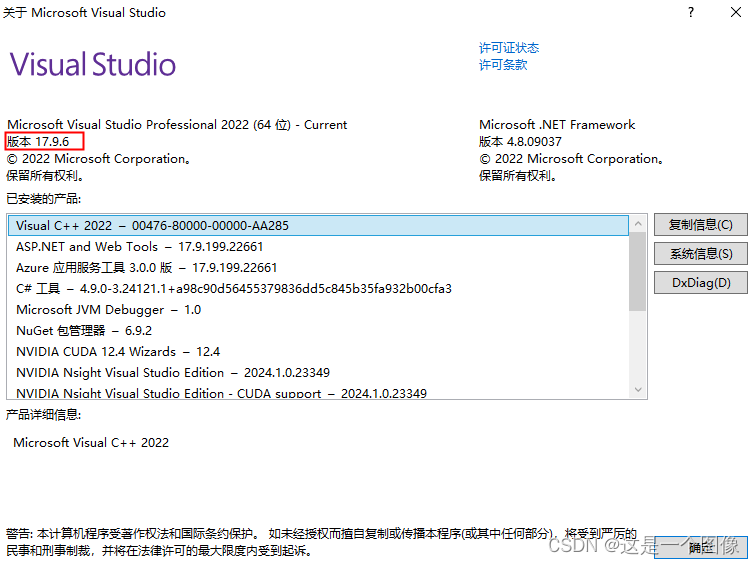
由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题
由于找不到MSVCP120D.dll,无法继续执行代码。重新安装程序可能会解决此问题 一、问题详细描述二、问题产生背景三、问题原因四、解决办法1、安装缺少的库2、直接更换更高版本的opencv 五、vs版本对应vc1、版本对应2、vs对应vc查看方法 一、问题详细描述 同样可能会报 ÿ…...

【前端】输入时字符跳动动画实现
输入时字符跳动动画实现 在前端开发中,为了提升用户体验,我们经常需要为用户的交互行为提供即时的反馈。这不仅让用户知道他们的操作有了响应,还可以让整个界面看起来更加生动、有趣。本文将通过一个简单的例子讲解如何实现在用户输入字符时…...

C语言面试重点问题
1. 冒泡排序法 2. strlen、strcpy、strcat、strcmp的用法和原理 3. 大小端的区分 3.1 主函数区分大小端 #include <stdio.h>int main(void) {int num 0x11223344;char *p (char *)#if (0x11 *p){printf("大端!\n");}else if (0x44 *p){printf(…...

antlr4略解
文章目录 1. antlr4是用来干什么的?2. 什么是lexer和parser?3. 使用antlr4生成某语言的lexer和parser的具体过程4. 其他 1. antlr4是用来干什么的? 是用来生成某语言lexer和parser的。 通俗点说,就是输入一个语言的规则描述文件&…...

超级好用的C++实用库之文件目录操作
💡 需要该C实用库源码的大佬们,可扫码关注文章末尾的微信公众号二维码,或搜索微信公众号“希望睿智”。添加关注后,输入消息“超级好用的C实用库”,即可获得源码的下载链接。 概述 文件和目录操作是操作系统层面上的基…...
结合kimi chat的爬虫实战思路
背景 想钻研一下项目组件,找找之后的学习方向。不能自以为是,所以借着网开源项目网站上公布的项目内容看一下,那些是我可以努力去学习的(入门的)。首先需要获取相关内容,于是爬取整理。 任务1:…...

UnsupportedClassVersionError异常如何解决?
下面是异常报错的详细描述 java -version java version "17.0.11" 2024-04-16 LTS Java(TM) SE Runtime Environment (build 17.0.117-LTS-207) Java HotSpot(TM) 64-Bit Server VM (build 17.0.117-LTS-207, mixed mode, sharing) 环境变量已经是jdk17,但…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
