数据结构中的栈(C语言版)
一.栈的概念
栈是一种常见的数据结构,它遵循后进先出的原则。栈可以看作是一种容器,其中的元素按照一种特定的顺序进行插入和删除操作。
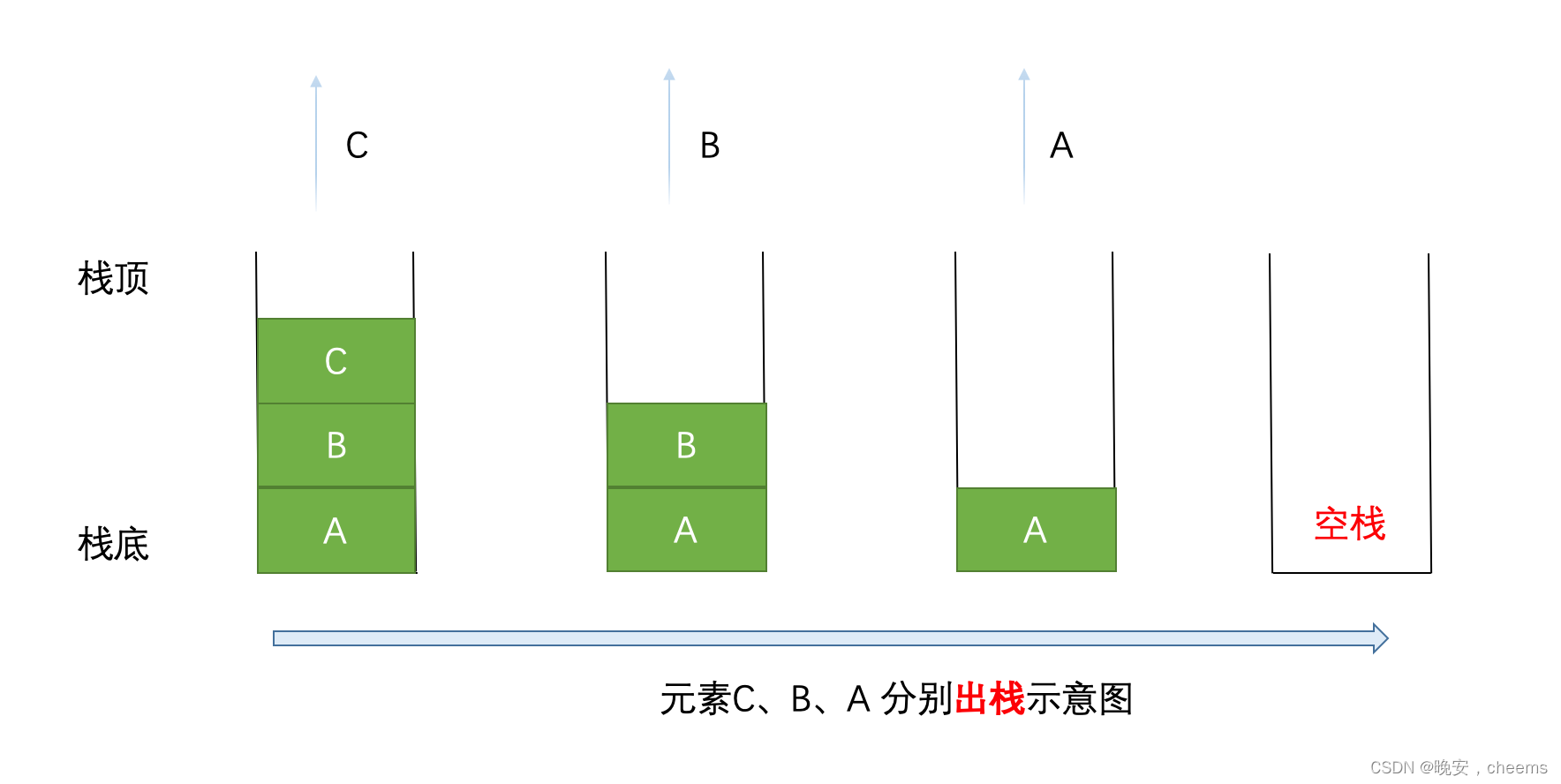
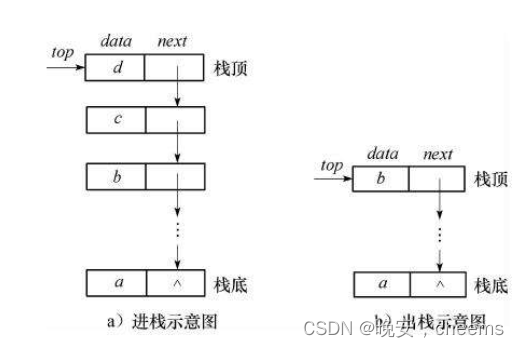
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈。出数据也在栈顶。
1.栈的特点
1.元素的插入和删除操作只能在栈的一端进行,该端被称为栈顶。
2.最后插入的元素是第一个被删除的元素,因此称为后进先出。
3.栈中的元素没有编号或索引,只有栈顶指针来指示栈的当前位置。
2.栈的优点
-
简单高效:栈的操作是基于后进先出(LIFO)的原则,入栈和出栈操作都只涉及栈顶元素,因此操作的时间复杂度都是O(1),使得栈的操作非常高效。
-
空间效率高:栈的底层实现可以使用数组或链表,无论是使用静态数组还是动态链表,都可以根据实际需要灵活分配内存,因此在空间利用上比较高效。
-
递归和回溯:栈在递归和回溯算法中扮演着重要的角色。递归函数调用时会将当前函数的状态(包括局部变量、返回地址等)压入栈中,当递归函数返回时,栈顶的状态会被弹出,恢复到上一层递归函数的状态。
-
撤销操作:栈可以用于实现撤销操作,比如文本编辑器中的撤销功能。每当执行一个操作时,将操作的状态存储在栈中,当需要撤销时,只需从栈中弹出最近的状态。
3.栈的缺点
-
容量限制:栈的容量是有限的,无论是基于数组还是链表实现的栈,都会受到内存大小的限制。当栈的元素个数超过容量时,会发生栈上溢(stack overflow)的错误。
-
无随机访问:栈的特点是只能在栈顶进行插入和删除操作,没有提供随机访问的能力。如果需要访问或修改栈中的其他元素,必须先将栈顶的元素弹出,直到达到目标位置。
-
不灵活:栈的特性决定了它的使用场景受到一定的限制。对于需要随机访问、频繁插入和删除的场景,栈可能不是最佳选择。
二.栈的功能
栈作为一种数据结构,具有以下几个主要的功能:
-
入栈:将元素添加到栈的顶部(栈顶)。新元素成为栈顶,原有的栈顶元素依次向下移动。入栈操作可以用于将数据添加到栈中。
-
出栈:从栈的顶部(栈顶)移除元素。被移除的元素是最后一个入栈的元素,即栈顶元素。出栈操作会改变栈的结构,并返回被移除的元素。
-
获取栈顶元素:获取栈顶的元素,但不对栈进行修改。这个操作可以让我们查看栈顶的元素,而不改变栈的结构。
-
判断栈是否为空:检查栈是否不包含任何元素。如果栈中没有元素,即栈为空,该函数返回真;否则,返回假。
-
判断栈是否已满:检查栈是否已达到其容量上限。对于基于数组实现的栈,如果数组已满,即栈已满,该函数返回真;否则,返回假。
三.栈的实现
1.创建栈
创建一个结构体,里面的成员是数组以及指针。(在这里,为了大家能够方便理解,用静态的顺序表来实现)
#include <stdio.h>
#define MAX_SIZE 100typedef struct {int data[MAX_SIZE]; // 用于存储栈中的元素int top; // 栈顶指针,指向栈顶元素的索引
} Stack;2.初始化栈
将栈顶的指针初始化为-1,表示此栈为空。
// 初始化栈
void initStack(Stack* stack) {stack->top = -1; // 栈顶指针初始化为-1,表示栈为空
}3.判断栈是否为空
判断栈是否为空。如果栈顶指针top等于-1,表示栈为空,返回1;否则,返回0。
// 判断栈是否为空
int isEmpty(Stack* stack) {return stack->top == -1; // 栈为空时,栈顶指针为-1
}4. 判断是否已满
判断栈是否已满。如果栈顶指针top等于数组最大索引(MAX_SIZE - 1),表示栈已满,返回1;否则,返回0。
// 判断栈是否已满
int isFull(Stack* stack) {
return stack->top == MAX_SIZE - 1; // 栈满时,栈顶指针等于数组最大索引
}5.入栈
入栈操作。首先使用isFull函数检查栈是否已满,如果已满,则打印错误信息并返回;否则,将栈顶指针top加1,并将元素item放入栈顶位置data[top]。
// 入栈
void push(Stack* stack, int item) {
if (isFull(stack)) {
printf("Stack overflow!\n"); // 栈已满,无法入栈
return;
}
stack->data[++stack->top] = item; // 栈顶指针加1,并将元素放入栈顶
}6.出栈
出栈操作。首先使用isEmpty函数检查栈是否为空,如果为空,则打印错误信息并返回-1;否则,返回栈顶元素data[top],并将栈顶指针top减1。
// 出栈
int pop(Stack* stack) {
if (isEmpty(stack)) {
printf("Stack underflow!\n"); // 栈为空,无法出栈
return -1;
}
return stack->data[stack->top--]; // 返回栈顶元素,并将栈顶指针减1
}7.获取栈顶元素
获取栈顶元素。首先使用isEmpty函数检查栈是否为空,如果为空,则打印错误信息并返回-1;否则,返回栈顶元素data[top],但不修改栈的结构。
/ 获取栈顶元素
int peek(Stack* stack) {
if (isEmpty(stack)) {
printf("Stack is empty!\n"); // 栈为空,无栈顶元素
return -1;
}
return stack->data[stack->top]; // 返回栈顶元素,不修改栈的结构
}8.打印栈中元素
打印栈中的元素。首先使用isEmpty函数检查栈是否为空,如果为空,则打印提示信息;否则,使用循环从栈底到栈顶依次打印栈中的元素。
/ 打印栈中的元素(用于调试)
void printStack(Stack* stack) {
if (isEmpty(stack)) {
printf("Stack is empty!\n");
return;
}
printf("Stack: ");
for (int i = 0; i <= stack->top; i++) {
printf("%d ", stack->data[i]);
}
printf("\n");
}四.栈的源码呈现
#include <stdio.h>
#define MAX_SIZE 100typedef struct {int data[MAX_SIZE]; // 用于存储栈中的元素int top; // 栈顶指针,指向栈顶元素的索引
} Stack;// 初始化栈
void initStack(Stack* stack) {stack->top = -1; // 栈顶指针初始化为-1,表示栈为空
}// 判断栈是否为空
int isEmpty(Stack* stack) {return stack->top == -1; // 栈为空时,栈顶指针为-1
}// 判断栈是否已满
int isFull(Stack* stack) {return stack->top == MAX_SIZE - 1; // 栈满时,栈顶指针等于数组最大索引
}// 入栈
void push(Stack* stack, int item) {if (isFull(stack)) {printf("Stack overflow!\n"); // 栈已满,无法入栈return;}stack->data[++stack->top] = item; // 栈顶指针加1,并将元素放入栈顶
}// 出栈
int pop(Stack* stack) {if (isEmpty(stack)) {printf("Stack underflow!\n"); // 栈为空,无法出栈return -1;}return stack->data[stack->top--]; // 返回栈顶元素,并将栈顶指针减1
}// 获取栈顶元素
int peek(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty!\n"); // 栈为空,无栈顶元素return -1;}return stack->data[stack->top]; // 返回栈顶元素,不修改栈的结构
}// 打印栈中的元素(用于调试)
void printStack(Stack* stack) {if (isEmpty(stack)) {printf("Stack is empty!\n");return;}printf("Stack: ");for (int i = 0; i <= stack->top; i++) {printf("%d ", stack->data[i]);}printf("\n");
}// 主函数用于测试栈的功能
int main() {Stack stack;initStack(&stack); // 初始化栈push(&stack, 10);push(&stack, 20);push(&stack, 30);printStack(&stack); // 打印栈中的元素printf("Top element: %d\n", peek(&stack)); // 获取栈顶元素while (!isEmpty(&stack)) {printf("Popped element: %d\n", pop(&stack)); // 依次出栈并输出元素}return 0;
}相关文章:

数据结构中的栈(C语言版)
一.栈的概念 栈是一种常见的数据结构,它遵循后进先出的原则。栈可以看作是一种容器,其中的元素按照一种特定的顺序进行插入和删除操作。 压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。 出栈:栈的删除操作叫做…...
 无重叠区间 划分字母区间 合并区间)
(贪心05) 无重叠区间 划分字母区间 合并区间
一、无重叠区间 力扣第435题 第一种方法: 个人思路: 按照区间左边界排序,然后从左开始遍历,每遍历到一个区间就要保证该区间之前的集合为不重叠区间(贪心,局部最优解)。 难点在于如何把新遍历…...
入门)
简单网络管理协议(SNMP)入门
目录 概述 SMI(对象命名、数据类型、编码方法) 对象命名 数据类型 编码方法 MIB(版本、分组、对象定义、变量访问) 版本 分组 对象定义 变量访问 SNMP 实现机制与报文分析 协议操作 报文格式 实现机制 验证分析 SN…...
1366 - 1372 题)
leetcode解题思路分析(一百五十七)1366 - 1372 题
通过投票对团队排名 现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。 排名规则如下: 参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在…...

药物代谢动力学学习笔记
一、基本概念 二、经典房室模型 三、非线性药物代谢动力学 四、非房室模型 五、药代动力学与药效动力学 六、生物等效性评价 七、生物样品分析方法 基本概念 生物样品:生物机体的全血、血浆、血清、粪便、尿液或其他组织的样品 特异性,specificity&…...
IDEA中git的常用操作(保姆级教学)
IDEA中git的常用操作(保姆级教学) 以下是git的工作原理,觉得繁琐的可以跳过不看 Workspace:工作区 (平时存放代码的地方) Index / Stage:暂存区(用于临时存放存放你的改动,事实上就是一个文件&…...
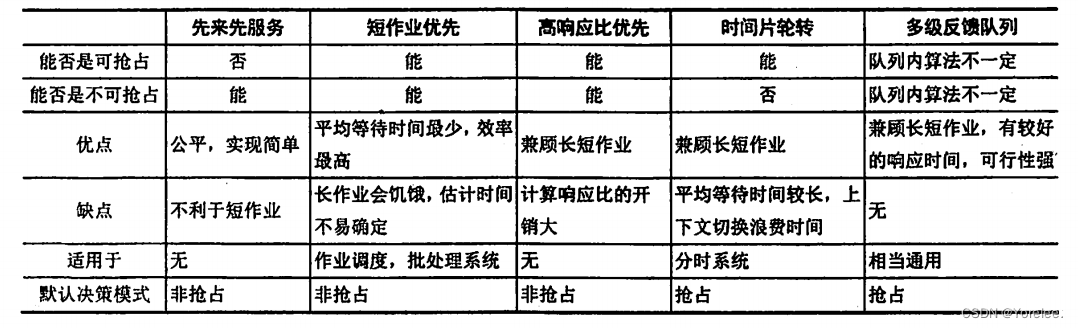
保研面试408复习 3——操作系统
文章目录 1、操作系统一、进程有哪几种状态,状态之间的转换、二、调度策略a.处理机调度分为三级:b.调度算法 标记文字记忆,加粗文字注意,普通文字理解。 为什么越写越少? 问就是在打瓦。(bushi) 1、操作系统 一、进程…...
)
【代码随想录37期】Day02 有序数组的平方、长度最小的子数组、螺旋矩阵Ⅱ(施工中)
有序数组的平方 977. 有序数组的平方 - 力扣(LeetCode) v1.0:直接暴力 4分半做出来,用sort api class Solution { public:vector<int> sortedSquares(vector<int>& nums) {vector<int> result;for(int i 0; i<…...
通俗的理解网关的概念的用途(三):你的数据包是如何到达下一层的
其实,这一章我写不好,因为这其中会涉及到一些计算和一些广播等概念,本人不善于此项。在此略述,可以参考。 每台设备的不同连接在获得有效的IP地址后,会根据IP地址的规则和掩码的规则,在操作系统和交换机&a…...
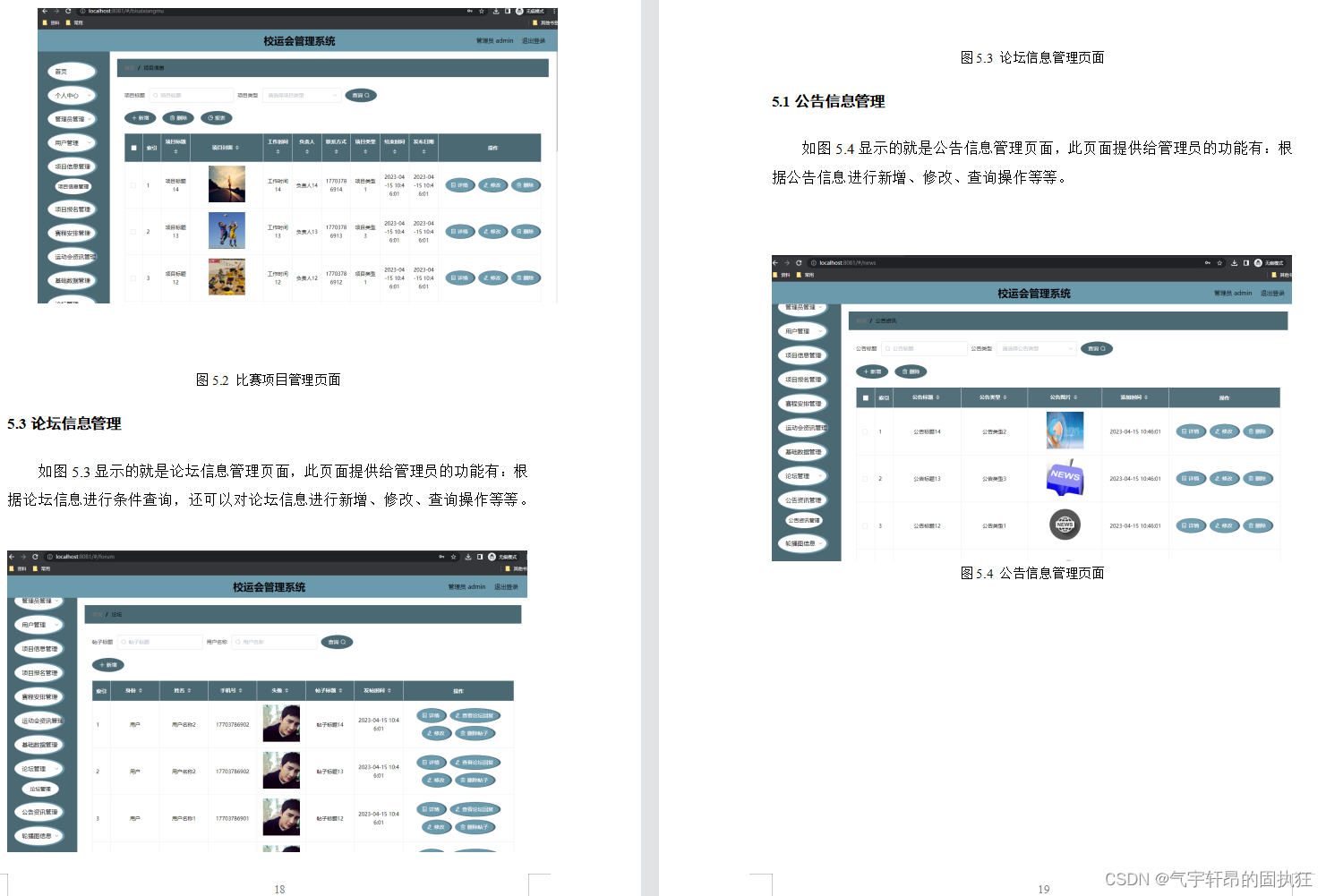
基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&a…...
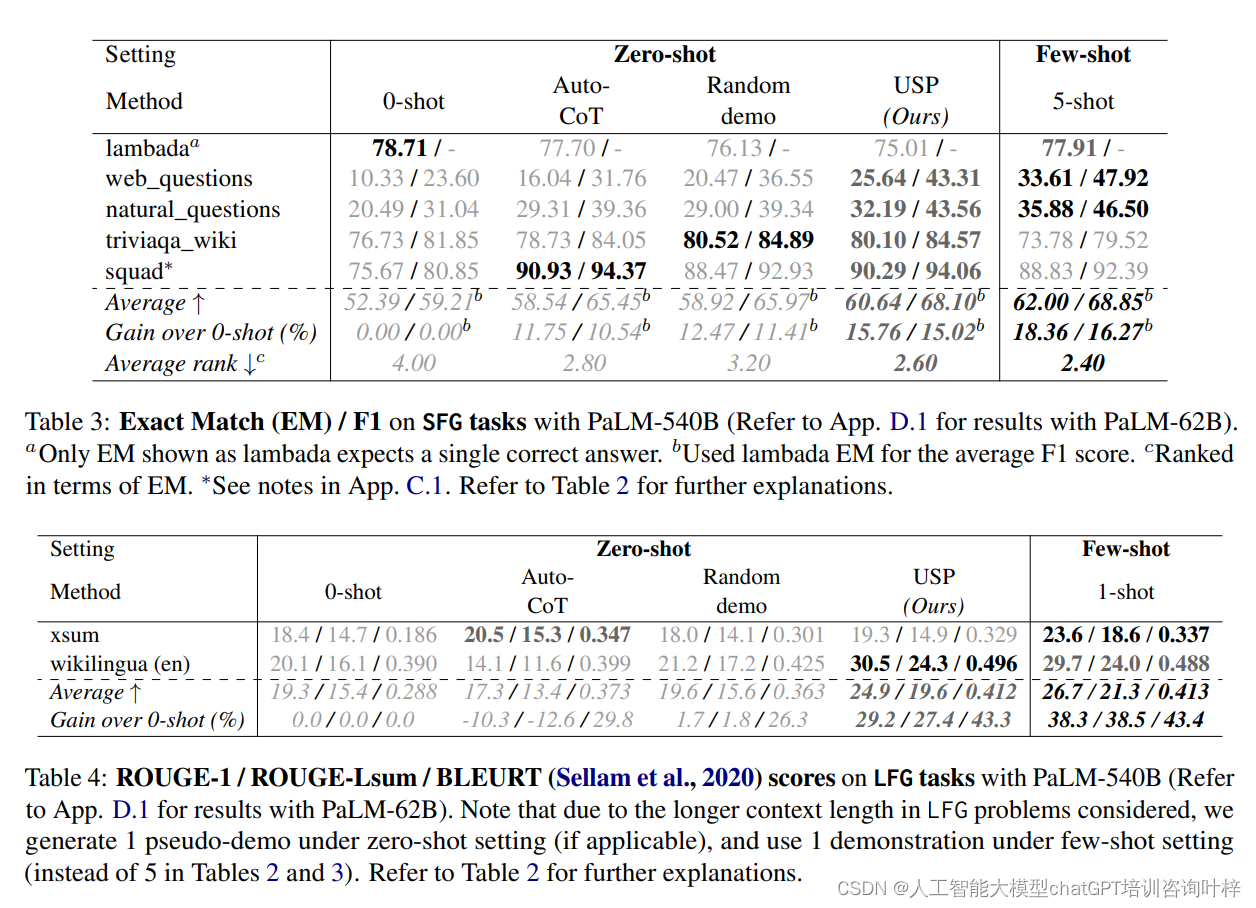
USP技术提升大语言模型的零样本学习能力
大语言模型(LLMs)在零样本和少样本学习能力上取得了显著进展,这通常通过上下文学习(in-context learning, ICL)和提示(prompting)来实现。然而,零样本性能通常较弱,因为缺…...
)
前端安全防护实战:XSS、CSRF防御与同源策略详解(react 案例)
前端安全防护实战中,主要涉及三个方面:XSS (Cross-Site Scripting) 攻击的防御、CSRF (Cross-Site Request Forgery) 攻击的防御,以及浏览器的同源策略。以下是这三个方面的详细说明: XSS 防御详解 XSS 概述 XSS攻击是一种让攻…...
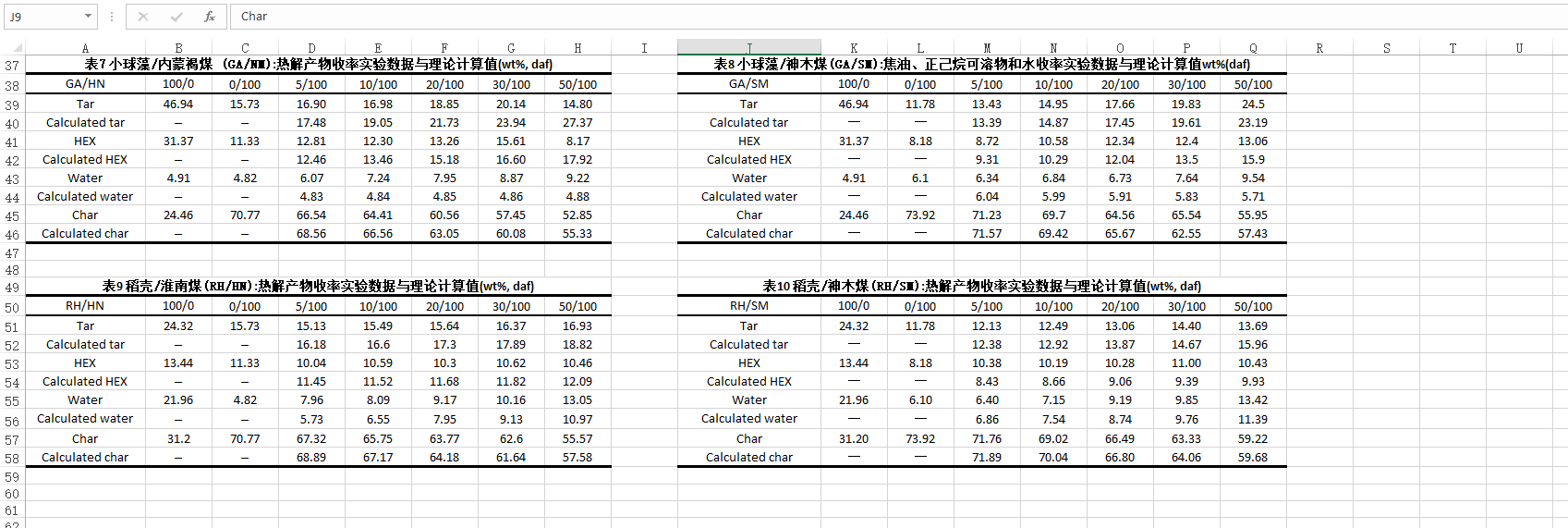
2024C题生物质和煤共热解问题的研究 详细思路
背景 随着全球能源需求的不断增长和对可再生能源的追求,生物质和煤共热解作为一种潜在的能源转化技术备受关注。生物质是指可再生能源,源自植物和动物的有机物质,而煤则是一种化石燃料。** 在共热解过程中,生物质和煤在高温和缺氧…...

智慧旅游引领未来风尚,科技助力旅行更精彩:科技的力量推动旅游业创新发展,为旅行者带来更加便捷、高效和智能的旅行服务
目录 一、引言 二、智慧旅游的概念与特点 (一)智慧旅游的概念 (二)智慧旅游的特点 三、科技推动旅游业创新发展 (一)大数据技术的应用 (二)人工智能技术的应用 (…...
十.吊打面试官系列-Tomcat优化-通过压测Tomcat调优实战
前言 上一篇文章我们讲解了一下Tomcat底层的结构和执行原理,我们需要重点去掌握的是Tomcat的高内聚低耦合的设计,以及责任链模式,以及Tomcat NIO编程模式,这些是Tomcat比较核心的点,本篇文章我们将对Tomcat的参数做一…...
JVM调优—减少FullGC
背景 最近负责了一个审批流程新项目,带领了几个小伙伴,哼哧哼哧的干了3个月左右,终于在三月底完美上线了,好消息是线上客户用的很丝滑,除了几个非常规的业务提单之外,几乎没有什么大的问题,但是…...

力扣 256. 粉刷房子 LCR 091. 粉刷房子 python AC
动态规划 class Solution:def minCost(self, costs):row, col len(costs), 3dp [[0] * col for _ in range(row 1)]for i in range(1, row 1):for j in range(col):dp[i][j] costs[i - 1][j - 1]if j 0:dp[i][j] min(dp[i - 1][1], dp[i - 1][2])elif j 1:dp[i][j] m…...
C++STL细节,底层实现,面试题04
文章目录 19. STL19.1. 序列容器19.1.1. vector19.1.1.1. 底层实现和特点19.1.1.2. 常用函数19.1.1.3. emplace_back() vs push_back() 19.1.2. array19.1.2.1. 底层实现和特点19.1.2.2. 常用函数 19.1.3. deque19.1.3.1. 底层实现和特点19.1.3.2. 常用函数 19.1.4 list19.1.4.…...

Linux查看Oracle数据库的环境变量
Linux查看Oracle数据库的环境变量 在Linux上查看Oracle数据库的环境变量,通常涉及检查当前shell会话中已设置的环境变量。这些环境变量可能包括ORACLE_HOME、ORACLE_SID、PATH(可能包含Oracle二进制文件的路径)等。 以下是几种方法来查看这…...
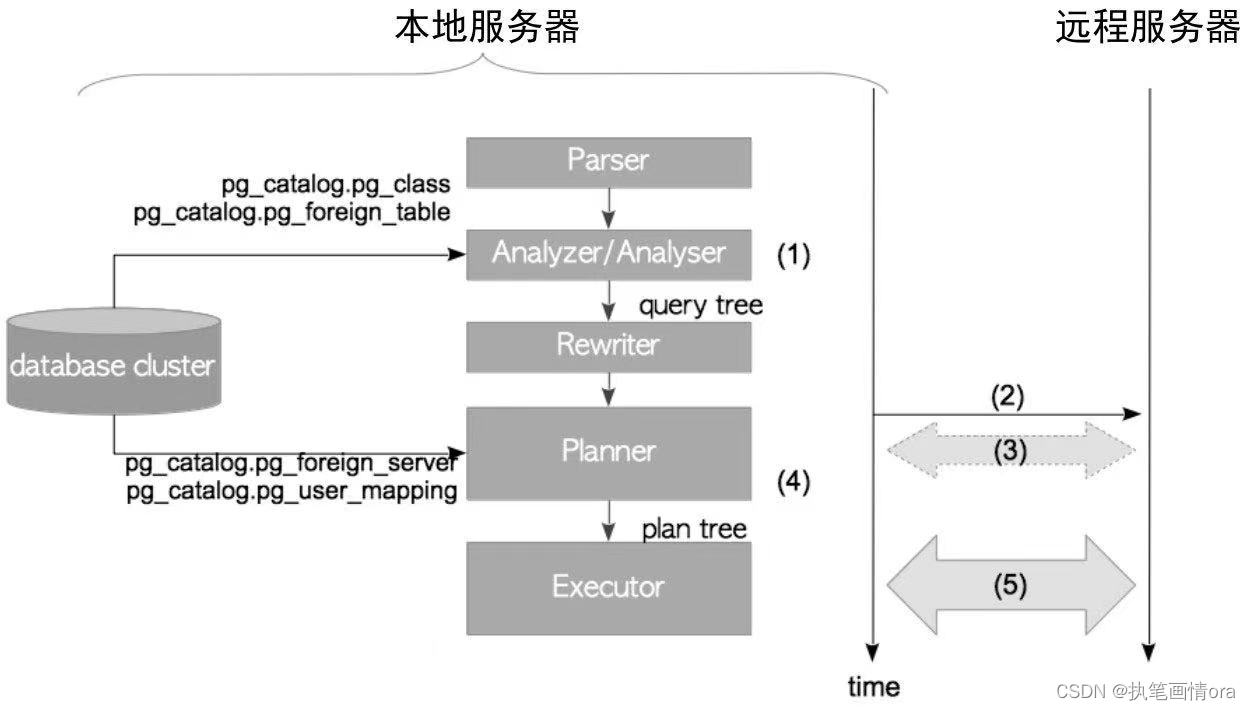
pg数据库学习知识要点分析-1
知识要点1 对象标识OID 在PostgreSQL内部,所有的数据库对象都通过相应的对象标识符(object identifier,oid)进行管理,这些标识符是无符号的4字节整型。数据库对象与相应oid 之间的关系存储在对应的系统目录中…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
