P2622 关灯问题
小小注解:
1.
vis:表示到达该状态的步数(min)+1,
因为我们是从开始状态 穷举,所以每次到一个新状态(之前没有到过的状态)就是最小步数。
如何判断是否是一个新状态呢,vis 知道,如果是新状态 vis=0;
另外,把开始状态设置为1,设置为 0 的话,程序就会把开始状态当作一个新状态,而开始状态当然不是一个新状态。
11.
开: 初始:1 0 1 0 关: 初始:1 0 1 0
开: 1 1 0 0 (|) 关: 1 1 0 0
结果: 1 1 1 0 结果: 0 0 1 0
初始 | 开 = 结果 ~关: 0 0 1 1 (&)
初始 &(~ 关) = 结果
111.
开始状态的得到:
例: n=4时;开始状态:1 1 1 1,即 (1<<n)-1 ;
注意:括号不能省,以为 1<<n-1 = 1<<(n-1);
#include<iostream>
#include<queue>
using namespace std;
int a[3300],b[3300]; //开灯 关灯 一个操作拆成两个 分别存在 a b中
int vis[3300]; //到达该状态的步数+1;
//对于一种状态 1改灯开 0关
int main(){int n,m; cin>>n>>m;for(int i=0;i<m;i++)for(int j=0;j<n;j++){int x; scanf("%d",&x);a[i]<<=1; b[i]<<=1;if(x==1) b[i]++;if(x==-1) a[i]++; }queue<int>q;q.push((1<<n)-1);vis[(1<<n)-1]=1;while(q.size()){int num=q.front(); q.pop();for(int i=0;i<m;i++){int temp=num|a[i];temp=temp&(~b[i]);if(vis[temp]) continue;vis[temp]=vis[num]+1; q.push(temp);if(temp==0){printf("%d",vis[0]-1); return 0;}}}printf("-1");return 0;
}相关文章:

P2622 关灯问题
小小注解: 1. vis:表示到达该状态的步数(min)1, 因为我们是从开始状态 穷举,所以每次到一个新状态(之前没有到过的状态)就是最小步数。 如何判断是否是一个新状态呢,…...
从头开始的建材类电商小程序开发指南
在当今数字化时代,小程序已经成为了许多企业推广和销售的重要渠道。对于建筑材料行业来说,开发一个属于自己的小程序商城不仅可以提升产品曝光度,还可以提供更好的用户购物体验。下面,我们将逐步教你如何开发建筑材料行业小程序。…...
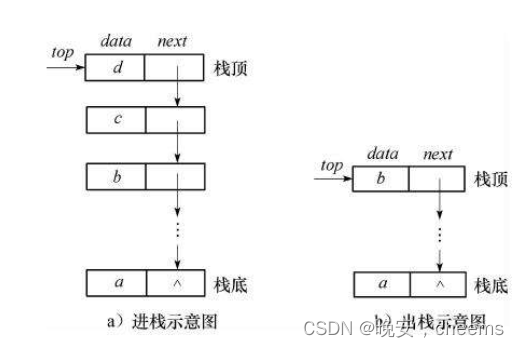
数据结构中的栈(C语言版)
一.栈的概念 栈是一种常见的数据结构,它遵循后进先出的原则。栈可以看作是一种容器,其中的元素按照一种特定的顺序进行插入和删除操作。 压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。 出栈:栈的删除操作叫做…...
 无重叠区间 划分字母区间 合并区间)
(贪心05) 无重叠区间 划分字母区间 合并区间
一、无重叠区间 力扣第435题 第一种方法: 个人思路: 按照区间左边界排序,然后从左开始遍历,每遍历到一个区间就要保证该区间之前的集合为不重叠区间(贪心,局部最优解)。 难点在于如何把新遍历…...
入门)
简单网络管理协议(SNMP)入门
目录 概述 SMI(对象命名、数据类型、编码方法) 对象命名 数据类型 编码方法 MIB(版本、分组、对象定义、变量访问) 版本 分组 对象定义 变量访问 SNMP 实现机制与报文分析 协议操作 报文格式 实现机制 验证分析 SN…...
1366 - 1372 题)
leetcode解题思路分析(一百五十七)1366 - 1372 题
通过投票对团队排名 现在有一个特殊的排名系统,依据参赛团队在投票人心中的次序进行排名,每个投票者都需要按从高到低的顺序对参与排名的所有团队进行排位。 排名规则如下: 参赛团队的排名次序依照其所获「排位第一」的票的多少决定。如果存在…...

药物代谢动力学学习笔记
一、基本概念 二、经典房室模型 三、非线性药物代谢动力学 四、非房室模型 五、药代动力学与药效动力学 六、生物等效性评价 七、生物样品分析方法 基本概念 生物样品:生物机体的全血、血浆、血清、粪便、尿液或其他组织的样品 特异性,specificity&…...
IDEA中git的常用操作(保姆级教学)
IDEA中git的常用操作(保姆级教学) 以下是git的工作原理,觉得繁琐的可以跳过不看 Workspace:工作区 (平时存放代码的地方) Index / Stage:暂存区(用于临时存放存放你的改动,事实上就是一个文件&…...
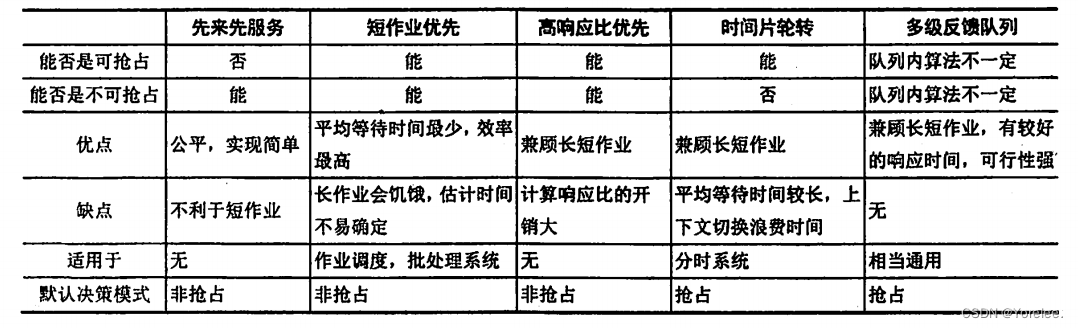
保研面试408复习 3——操作系统
文章目录 1、操作系统一、进程有哪几种状态,状态之间的转换、二、调度策略a.处理机调度分为三级:b.调度算法 标记文字记忆,加粗文字注意,普通文字理解。 为什么越写越少? 问就是在打瓦。(bushi) 1、操作系统 一、进程…...
)
【代码随想录37期】Day02 有序数组的平方、长度最小的子数组、螺旋矩阵Ⅱ(施工中)
有序数组的平方 977. 有序数组的平方 - 力扣(LeetCode) v1.0:直接暴力 4分半做出来,用sort api class Solution { public:vector<int> sortedSquares(vector<int>& nums) {vector<int> result;for(int i 0; i<…...
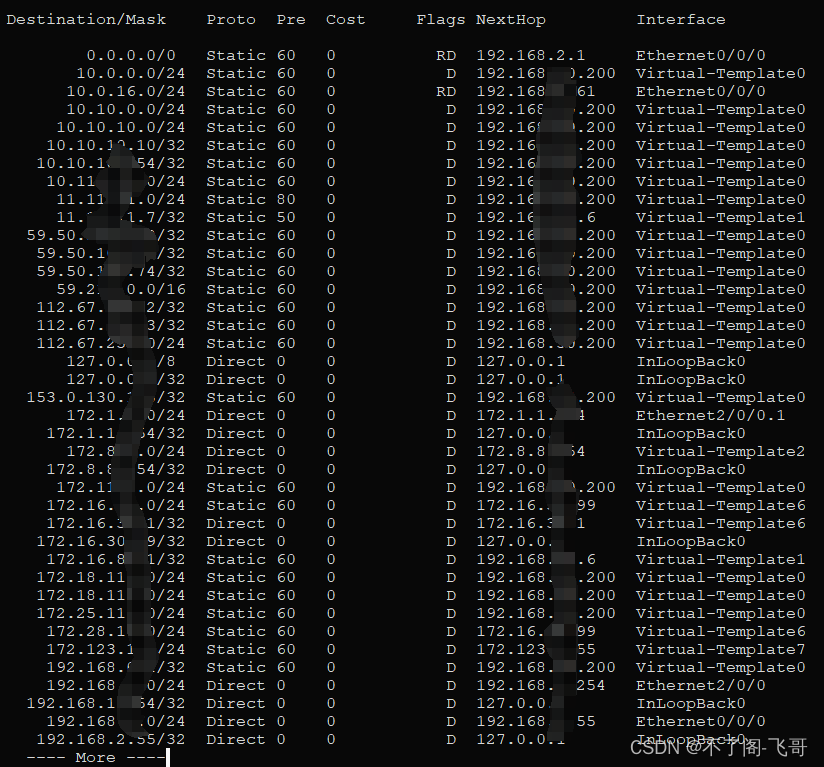
通俗的理解网关的概念的用途(三):你的数据包是如何到达下一层的
其实,这一章我写不好,因为这其中会涉及到一些计算和一些广播等概念,本人不善于此项。在此略述,可以参考。 每台设备的不同连接在获得有效的IP地址后,会根据IP地址的规则和掩码的规则,在操作系统和交换机&a…...
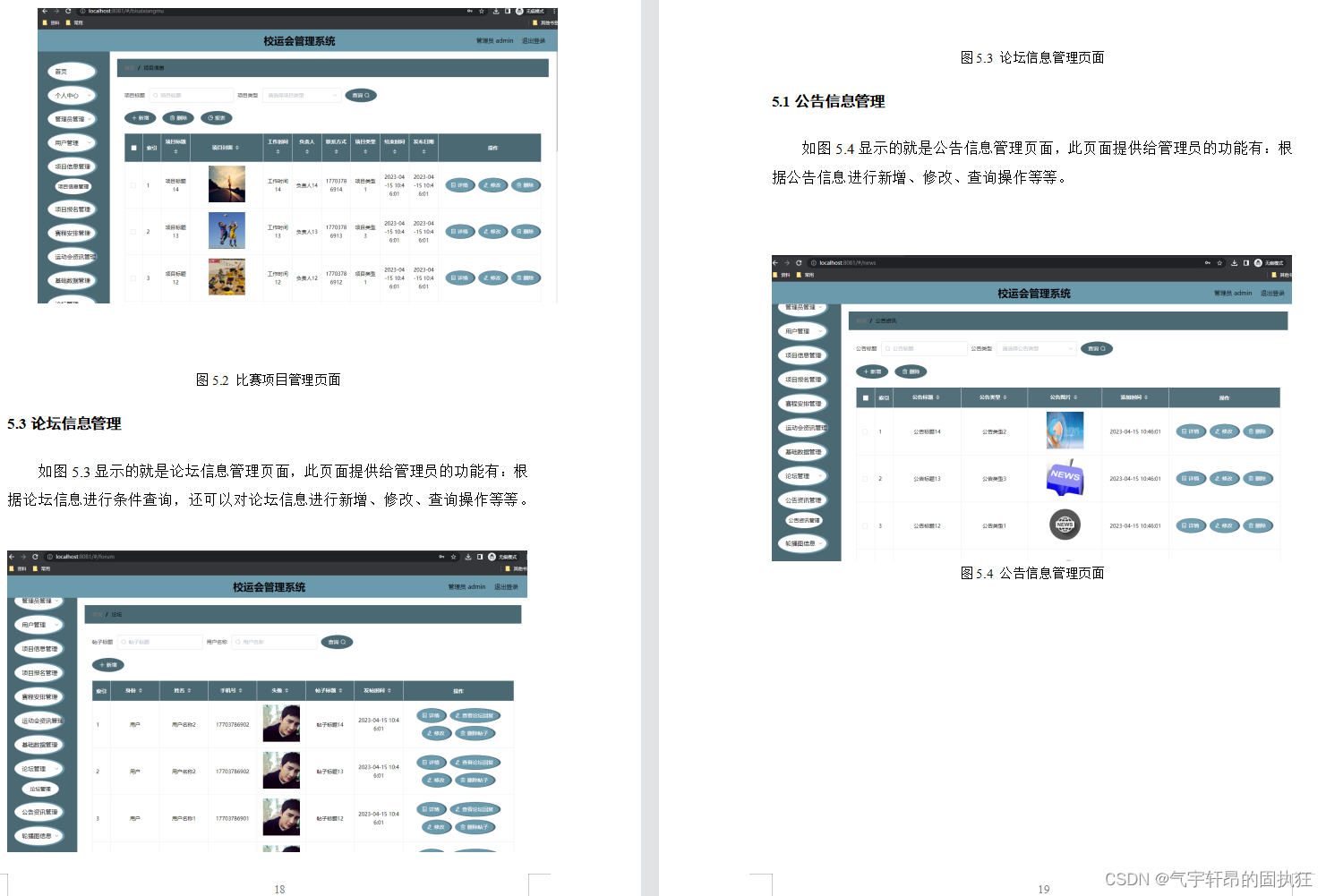
基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的校运会管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&a…...
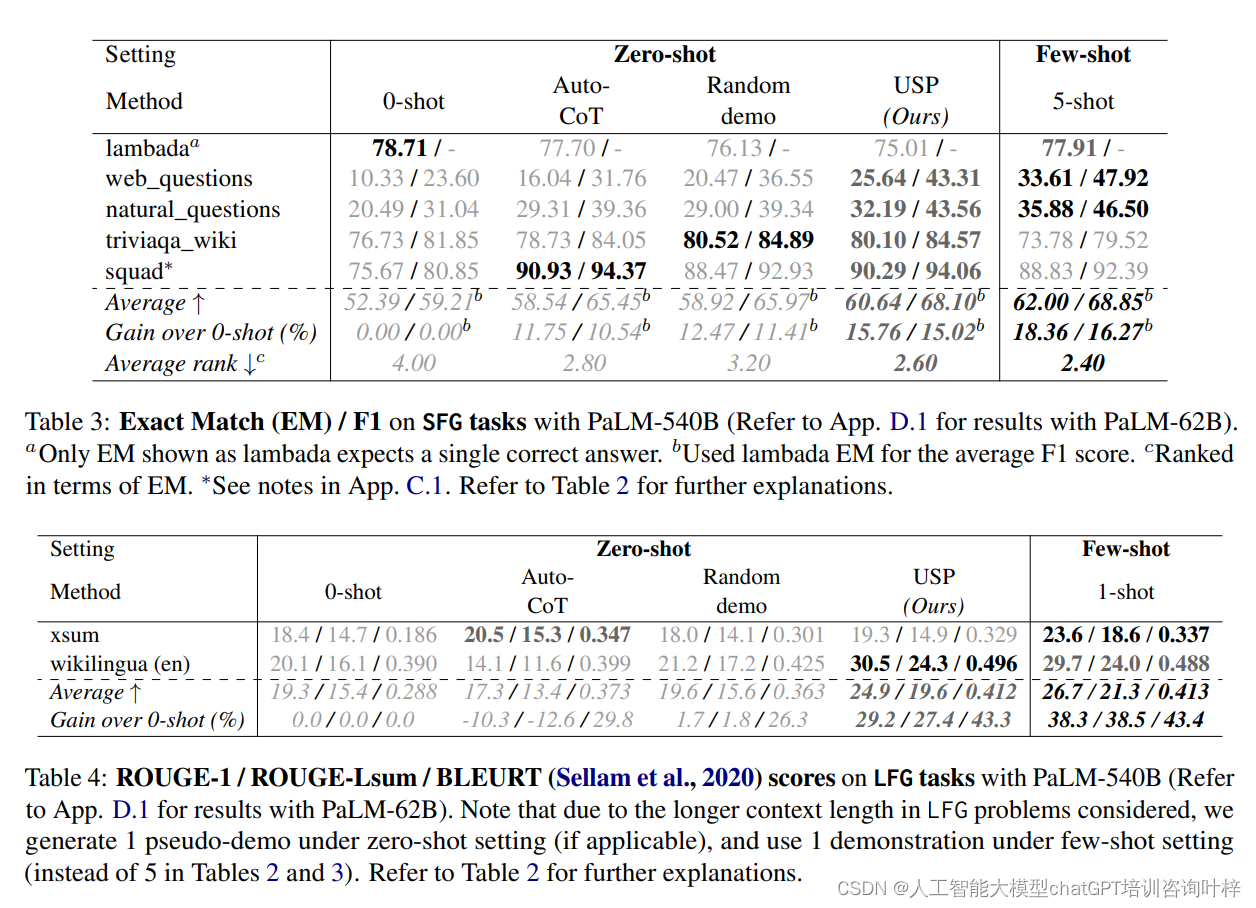
USP技术提升大语言模型的零样本学习能力
大语言模型(LLMs)在零样本和少样本学习能力上取得了显著进展,这通常通过上下文学习(in-context learning, ICL)和提示(prompting)来实现。然而,零样本性能通常较弱,因为缺…...
)
前端安全防护实战:XSS、CSRF防御与同源策略详解(react 案例)
前端安全防护实战中,主要涉及三个方面:XSS (Cross-Site Scripting) 攻击的防御、CSRF (Cross-Site Request Forgery) 攻击的防御,以及浏览器的同源策略。以下是这三个方面的详细说明: XSS 防御详解 XSS 概述 XSS攻击是一种让攻…...
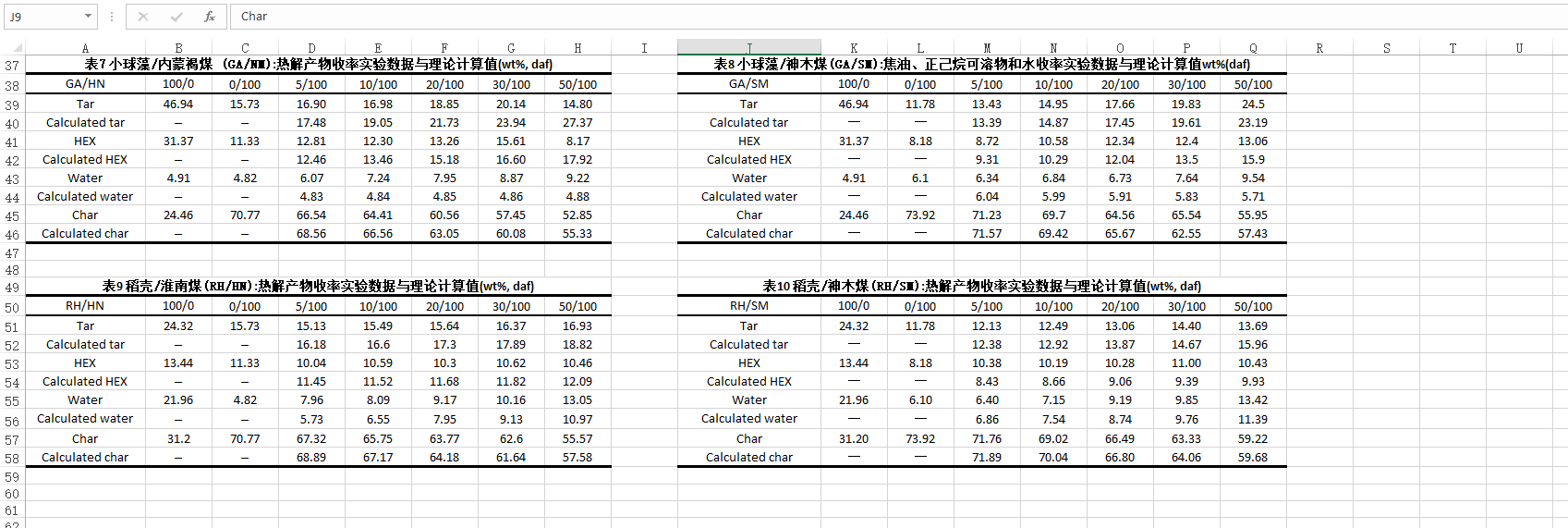
2024C题生物质和煤共热解问题的研究 详细思路
背景 随着全球能源需求的不断增长和对可再生能源的追求,生物质和煤共热解作为一种潜在的能源转化技术备受关注。生物质是指可再生能源,源自植物和动物的有机物质,而煤则是一种化石燃料。** 在共热解过程中,生物质和煤在高温和缺氧…...

智慧旅游引领未来风尚,科技助力旅行更精彩:科技的力量推动旅游业创新发展,为旅行者带来更加便捷、高效和智能的旅行服务
目录 一、引言 二、智慧旅游的概念与特点 (一)智慧旅游的概念 (二)智慧旅游的特点 三、科技推动旅游业创新发展 (一)大数据技术的应用 (二)人工智能技术的应用 (…...
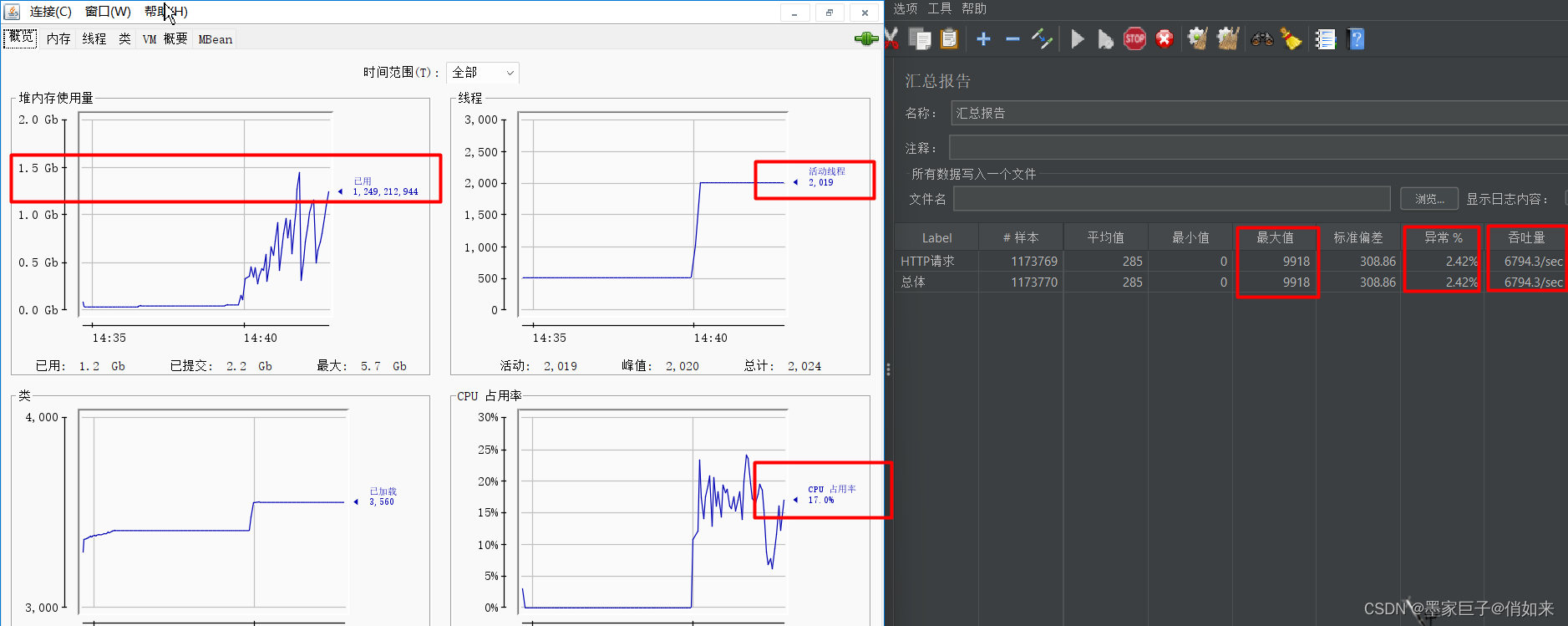
十.吊打面试官系列-Tomcat优化-通过压测Tomcat调优实战
前言 上一篇文章我们讲解了一下Tomcat底层的结构和执行原理,我们需要重点去掌握的是Tomcat的高内聚低耦合的设计,以及责任链模式,以及Tomcat NIO编程模式,这些是Tomcat比较核心的点,本篇文章我们将对Tomcat的参数做一…...
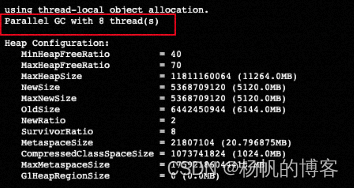
JVM调优—减少FullGC
背景 最近负责了一个审批流程新项目,带领了几个小伙伴,哼哧哼哧的干了3个月左右,终于在三月底完美上线了,好消息是线上客户用的很丝滑,除了几个非常规的业务提单之外,几乎没有什么大的问题,但是…...

力扣 256. 粉刷房子 LCR 091. 粉刷房子 python AC
动态规划 class Solution:def minCost(self, costs):row, col len(costs), 3dp [[0] * col for _ in range(row 1)]for i in range(1, row 1):for j in range(col):dp[i][j] costs[i - 1][j - 1]if j 0:dp[i][j] min(dp[i - 1][1], dp[i - 1][2])elif j 1:dp[i][j] m…...
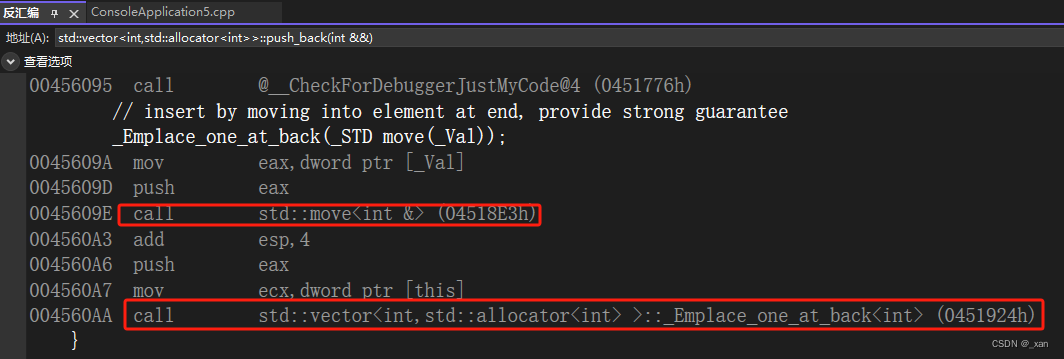
C++STL细节,底层实现,面试题04
文章目录 19. STL19.1. 序列容器19.1.1. vector19.1.1.1. 底层实现和特点19.1.1.2. 常用函数19.1.1.3. emplace_back() vs push_back() 19.1.2. array19.1.2.1. 底层实现和特点19.1.2.2. 常用函数 19.1.3. deque19.1.3.1. 底层实现和特点19.1.3.2. 常用函数 19.1.4 list19.1.4.…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
