python sympy库
sympy库是python的符号运算库,是电脑辅助简单数学函数计算的好工具。本文简单记录了一下有关sympy的方法。建议使用jupyter notebook,这样输出的函数很好看。
文章目录
- sympy基础
- 安装
- 自变量(Symbols)
- 函数表达式(Expr)
- 变量替换与赋值
- 精确求值
- 微分
- 积分
- Taylor展开
- 一元展开
- 多元展开
- 查看展开项
- 极限
- 解方程
- 画图
sympy基础
安装
pip install sympy
自变量(Symbols)
通过symbols方法将字符串声明为数学函数的变量,这些变量往往是函数的自变量。
import sympy
# 声明单个变量
x = sympy.symbols('x')# 声明多个变量(以下方法皆可)
x,y = sympy.symbols(['x','y'])
x,y = sympy.symbols("x,y")
x,y = sympy.symbols("x y")
函数表达式(Expr)
函数表达式通过变量的运算构造具体函数,或者通过Function函数构造抽象函数。
f = sympy.sqrt(3*x*y) +x*sympy.sin(y) +y**2 +x**3 # 具体函数
u = sympy.Function('u') # 抽象函数
变量替换与赋值
expr.subs()可以实现变量替换,替换成数字实现赋值。
g1 = f.subs(x,y) # 将f表达式中的x换成y,并将替换的结果,赋给g
g2 = f.subs({x:2*x, y:2*y}) #多次替换,字典
g3 = f.subs({x:1,y:2})
精确求值
expr.evalf(n)可以求一个表达式的保留n位有效数字的精确值
g3 = f.subs({x:1,y:2})
print(g.evalf(4)) # 8.359
微分
sympy可以实现自动求微分,方法如下
h1 = sympy.diff(f,x) # f对x求微分
h1 = f.diff(x) # 同上
h2 = sympy.diff(f,x,2,y,1) # f对x求2次微分,对y求1次微分
积分
sympy可以实现自动求不定积分和定积分,区别在于是否传入积分上下限
l1 = sympy.integrate(f,x) # 不定积分
l2 = sympy.integrate(f,(x,1,3)) #定积分
Taylor展开
一元展开
sympy可以实现泰勒展开,具体函数抽象函数都可以。但是不能对多元函数同时泰勒展开。
taylor1 = sympy.series(f,x,0,4) # f对x在0处泰勒展开到4阶
taylor2 = sympy.series(f,x,0,4).removeO # f对x在0处泰勒展开到4阶,去除皮亚诺余项
taylor3 = sympy.series(u(x),x,0,4) # 抽象函数u对x在0处泰勒展开到4阶
多元展开
多元泰勒展开可以使用以下方法
参考链接:https://www.thinbug.com/q/23803320
def Taylor_polynomial_sympy(function_expression, variable_list, evaluation_point, degree):"""Mathematical formulation reference:https://math.libretexts.org/Bookshelves/Calculus/Supplemental_Modules_(Calculus)/Multivariable_Calculus/3%3A_Topics_in_Partial_Derivatives/Taylor__Polynomials_of_Functions_of_Two_Variables:param function_expression: Sympy expression of the function:param variable_list: list. All variables to be approximated (to be "Taylorized"):param evaluation_point: list. Coordinates, where the function will be expressed:param degree: int. Total degree of the Taylor polynomial:return: Returns a Sympy expression of the Taylor series up to a given degree, of a given multivariate expression, approximated as a multivariate polynomial evaluated at the evaluation_point"""from sympy import factorial, Matrix, prodimport itertoolsn_var = len(variable_list)point_coordinates = [(i, j) for i, j in (zip(variable_list, evaluation_point))] # list of tuples with variables and their evaluation_point coordinates, to later perform substitutionderiv_orders = list(itertools.product(range(degree + 1), repeat=n_var)) # list with exponentials of the partial derivativesderiv_orders = [deriv_orders[i] for i in range(len(deriv_orders)) if sum(deriv_orders[i]) <= degree] # Discarding some higher-order termsn_terms = len(deriv_orders)deriv_orders_as_input = [list(sum(list(zip(variable_list, deriv_orders[i])), ())) for i in range(n_terms)] # Individual degree of each partial derivative, of each termpolynomial = 0for i in range(n_terms):partial_derivatives_at_point = function_expression.diff(*deriv_orders_as_input[i]).subs(point_coordinates) # e.g. df/(dx*dy**2)denominator = prod([factorial(j) for j in deriv_orders[i]]) # e.g. (1! * 2!)distances_powered = prod([(Matrix(variable_list) - Matrix(evaluation_point))[j] ** deriv_orders[i][j] for j in range(n_var)]) # e.g. (x-x0)*(y-y0)**2polynomial += partial_derivatives_at_point / denominator * distances_poweredreturn polynomialTaylor_polynomial_sympy(u(x,y),[x,y],[0,0],2) #函数u对(x,y)在(0,0)处泰勒展开
查看展开项
taylor1.coeff(x) # 查看taylor1中x项(x-x0项)的系数。
极限
sympy可以实现求极限,注意极限方向
lim1 = sympy.limit(f, x, sympy.oo) # 趋于无穷
lim2 = sympy.limit(f, x, 0) # 趋于0,默认值 dir='+',也就是趋于+0
lim3 = sympy.limit(f, x, 0, dir="-") # 趋于0,默认值调整为dir='-',也就是趋于-0
解方程
sympy可以实现解方程,方法是令Expr=0,所以在解方程时,要先构造一个等于0的左端项。返回结果是一个列表,每一项是一个解。如果是方程组,解列表每一项是一个元组,元组对应位置是对应自变量的值。
func = f-3
sympy.solve(func,x) # 返回f=3时x的值
sympy.solve([x**2+y**2-1, x+y-1],[x,y]) #x^2+y^2=1;x+y=1
画图
sympy可以实现绘制函数图像,要先安装matplotlib库。
pip install matplotlib
sympy可以绘制一元函数、二元函数、隐函数的图像,方法如下
from sympy.plotting import plot,plot3d,plot_implicit
from sympy import Eq # 构造隐函数时使用# 绘制一元函数图像
plot(x**2,x) # 绘制以x为自变量的函数图像
plot(x**2,(x,-3,4)) # 绘制以x为自变量的函数图像,绘制区间限制在[-3,4]上
plot(x,x**2,x**3,(x,0,4)) # 绘制多个图像 # 绘制二元函数图像,呈现3D图
plot3d(x**2*y,(x,-10,10),(y,-10,10))# 绘制隐函数图像
plot_implicit(Eq(x**2+y**4,1),(x,-2,2),(y,-2,2))
相关文章:

python sympy库
sympy库是python的符号运算库,是电脑辅助简单数学函数计算的好工具。本文简单记录了一下有关sympy的方法。建议使用jupyter notebook,这样输出的函数很好看。 文章目录sympy基础安装自变量(Symbols)函数表达式(Expr&am…...

达梦数据库统计信息的导出导入
一、统计信息对象统计信息描述了对象数据的分布特征。统计信息是优化器的代价计算的依据,可以帮助优化器较精确地估算成本,对执行计划的选择起着至关重要的作用。统计信息的收集频率是一把双刃剑,频率太低导致统计信息滞后,频率太…...

信息系统基本知识(六)
大纲 信息系统与信息化信息系统开发方法常规信息系统集成技术软件工程新一代信息技术信息系统安全技术信息化发展与应用信息系统服务管理信息系统服务规划企业首席信息管及其责任 1.7 信息化发展与应用 我国在“十三五”规划纲要中,将培育人工智能、移动智能终端…...

<C++>智能指针
1. 智能指针 #define _CRT_SECURE_NO_WARNINGS #include<iostream> #include<memory> using namespace std;int div() {int a, b;cin >> a >> b;if (b 0)throw invalid_argument("除0错误");return a / b; }void func() {int* p1 new in…...

1.分析vmlinux可执行文件是如何生成的? 2.整理内核编译流程:uImage/zImage/Image/vmlinx之间关系
一、分析vmlinux可执行文件是如何生成的? 1、分析内核的底层 makefile 如下: vmlinux: scripts/link-vmlinux.sh vmlinux_prereq $(vmlinux-deps) FORCE$(call if_changed,link-vmlinux)vmlinux_prereq: $(vmlinux-deps) FORCE发现vmlinux的生成主要依…...
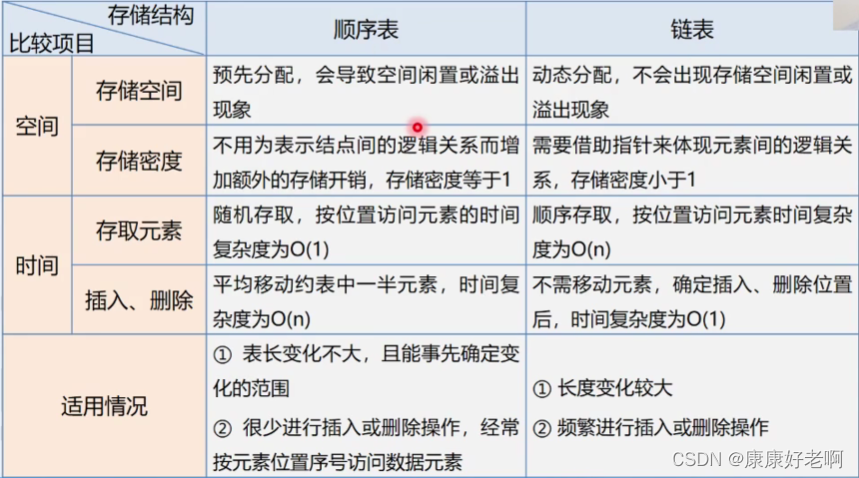
数据结构4——线性表3:线性表的链式结构
基本概念 链式存储结构用一组物理位置任意的存储单元来存放线性表的数据元素。 这组存储单元既可以是连续的又可以是不连续的甚至是零散分布在任意位置上的。所以链表中元素的逻辑次序和物理次序不一定相同。而正是因为这一点,所以我们要利用别的方法将这些…...

weblogic 忘记密码重置密码
解决:weblogic 忘记密码 weblogic安装后,很久不用,忘记访问控制台的用户名或者密码,可通过以下步骤来重置用户名密码。 版本:WebLogic Server 11g 说明:%DOMAIN_HOME%:指WebLogic Server 域(…...

安卓开发之动态设置网络访问地址
之前开发程序联测测接口的时候,因为要和不同的后台人员调接口,所以经常要先把程序里的ip地址改成后台人员给我的。每次都要先修改ip地址,之后编译运行一下,才能测试。但要是换了个后台人员,或者同时和2个后台人员测接口…...

深度学习模型训练工作汇报(3.8)
进行数据的初始整理的准备 主要是进行伪序列字典的设置,以及训练数据集的准备。 期间需要的一些问题包括在读取文件信息的时候,需要跳过文件的第一行或者前两行,如果使用循环判断的话,会多进行n次的运算,这是不划算的…...

【ns-3】添加nr(5G-LENA)模块
文章目录前言1. 下载5G-LENA源代码2. 配置并重新构建ns-3项目参考文献前言 本篇以ns-3.37为例介绍如何在ns-3中添加nr(5G-LENA)模块 [1]。5G-LENA是一个由Mobile Networks group CTTC(Centre Tecnolgic de Telecomunicacions de Catalunya&a…...
(模拟)(前缀和)(数组模拟哈希)(可二分)1236. 递增三元组)
(枚举)(模拟)(前缀和)(数组模拟哈希)(可二分)1236. 递增三元组
目录 题目链接 一些话 流程 套路 ac代码 题目链接 1236. 递增三元组 - AcWing题库 一些话 int f[N]; memset(f,0,sizeof f)影响不到f[N] 所以尽量不要对f[N]赋值,不要用f[N]操作 流程 //由三重暴力i,j,k因为三重暴力底下是分别用i和j,j和k作比较…...
)
mysql五种索引类型(实操版本)
为什么使用索引 最近学习了Mysql的索引,索引对于Mysql的高效运行是非常重要的,正确的使用索引可以大大的提高MySql的检索速度。通过索引可以大大的提升查询的速度。不过也会带来一些问题。比如会降低更新表的速度(因为不但要把保存数据还要保…...

微服务进阶之 SpringCloud Alibaba
文章目录微服务进阶🍓SpringCloud 有何劣势?🍓SpringCloud Alibaba 提供了什么?提示:以下是本篇文章正文内容,SpringCloud 系列学习将会持续更新 微服务进阶 🍓SpringCloud 有何劣势࿱…...

前端性能优化笔记2 第二章 度量
相关 Performance API 都在 window.performance 对象下 performance.now() 方法 精度精确到微妙获取的是把页面打开时间点作为基点的相对时间,不依赖操作系统的时间。 部分浏览器不支持 performance.now() 方法,可以用 Date.now() 模拟 performance.n…...
关于new和delete的一些思考,为什么不能在析构函数中调用delete释放对象的内存空间,new和delete的原理
最近在写代码的时候,觉得每次new出来的对象都需要去delete好麻烦,于是直接把delete写到了析构函数中,在析构函数里面写了句delete this,结果调用析构函数的时候死循环了,不是很理解原因,于是去研究了一下。…...

一场以数字技术深度影响和改造传统实业的新风口,正在开启
当数字经济的浪潮开始上演,一场以数字技术深度影响和改造传统实业的新风口,正在开启。对于诸多在互联网时代看似业已走入死胡同的物种来讲,可以说是打开了新的天窗。对于金融科技来讲,同样如此。以往,谈及金融科技&…...

【LeetCode】13. 罗马数字转整数
题目链接:https://leetcode.cn/problems/roman-to-integer/ 📕题目要求: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 例如, 罗马数字 2 写做 II ,即…...

2023/3/8集合之TreeSet HashSet简介 不含代码
TreeSet : 底层是由TreeMap维护的 无序的,不可重的 底层结构 : 红黑树(平衡二叉树) 特点 : 查询效率高,默认升序排序引用场景 : 适合应用在存储多个单个值的数据的集合,去重的,自动升序排序的场景新增方法:新增了一些与比较大小相关的方法 遍历方式 1)foreach 2)iterator 1测试…...

【面试1v1实景模拟】面试中常见的Java关键字详解
笑小枫专属目录老面👴:Java中有哪些关键字老面👴:简单介绍一下 final 关键字老面👴:简单介绍一下 this、super 关键字老面👴:简单介绍一下 static 关键字老面👴ÿ…...

MySQL8.0.16存储过程比5.7.22性能大幅下降
MySQL8.0.16存储过程比5.7.22性能大幅下降 1、背景 从5.7.22迁移数据库到8.0.16,发现存储过程执行性能大幅下降。原来在5版本上执行只需要3-5秒,到8版本上居然要达到上万秒。 5版本: call Calculation_Week() OK 时间: 3.122s 8版本&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
