【matlab基础知识代码】(十六)代数方程的图解法多项式型方程的准解析解方法



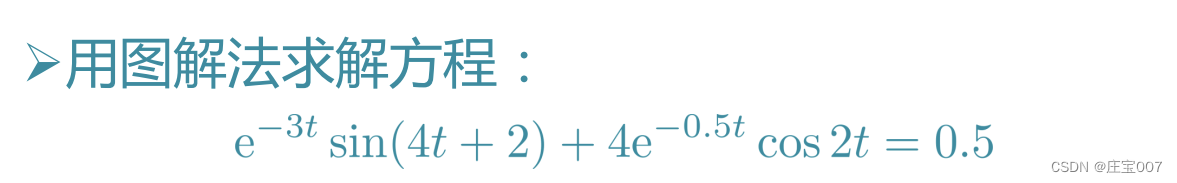
>> ezplot('exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5',[0 5]),
line([0 5],[0 0])
验证
>> t=0.6738;
>> exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5
ans =
-2.9852e-04

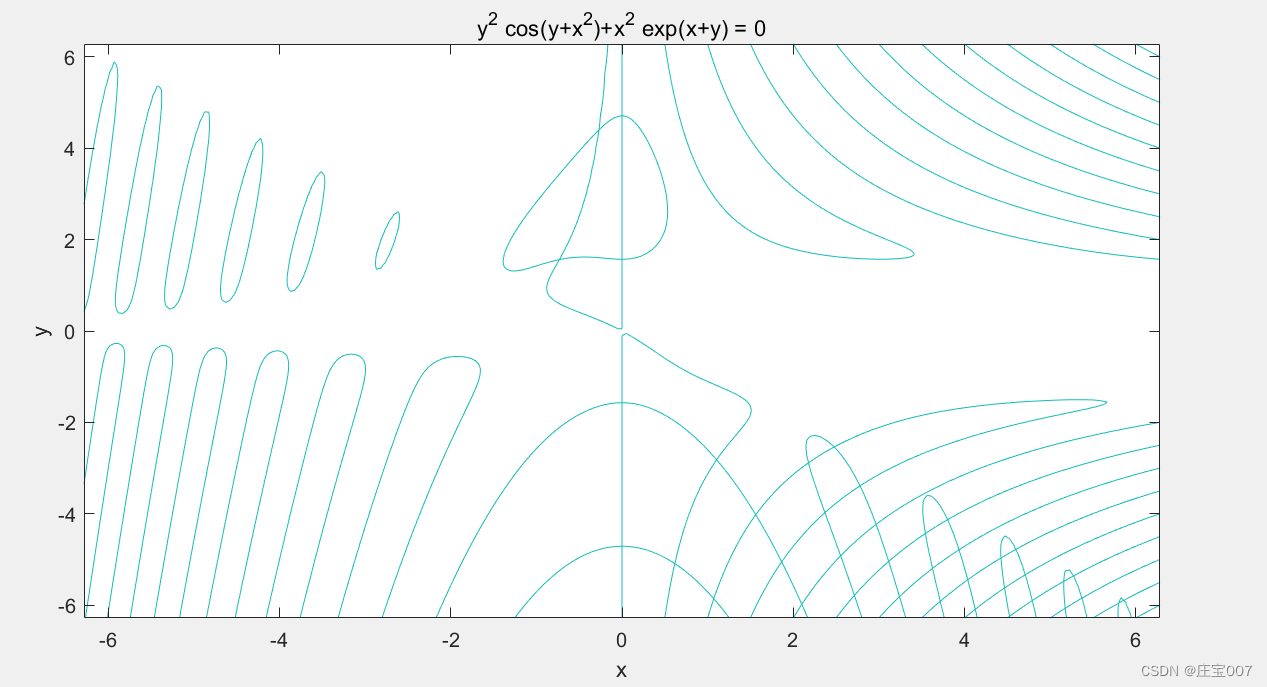
>> ezplot('x^2*exp(-x*y^2/2)+exp(-x/2)*sin(x*y)')
>> hold on; ezplot('y^2*cos(y+x^2)+x^2*exp(x+y)')

ezplot('x^2+y^2-1'); hold on, ezplot('0.75*x^3-y+0.9')

多项式型方程的准解析解方法

准解析解的精度要远远高于双精度意义下的数值解


>> syms x y; [x0 y0]=solve(x+y==35,2*x+4*y==94)x0 =23y0 =12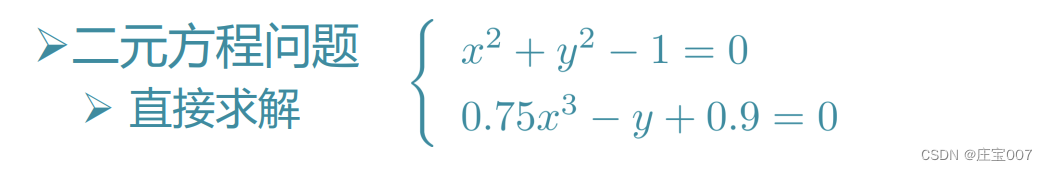
>> [x1,y1]=vpasolve(x^2+y^2-1==0,75*x^3/100-y+9/10==0)x1 =0.8663180988361181101678980941865 + 1.2153712664671427801318378544391i0.8663180988361181101678980941865 - 1.2153712664671427801318378544391i
- 0.55395176056834560077984413882735 - 0.35471976465080793456863789934944i
- 0.55395176056834560077984413882735 + 0.35471976465080793456863789934944i0.35696997189122287798839037801365-0.98170264842676789676449828873194y1 =- 1.4916064075658223174787216959257 + 0.7058820072140226775391882713884i
- 1.4916064075658223174787216959257 - 0.7058820072140226775391882713884i0.92933830226674362852985276677202 - 0.2114382218589592361562338176221i0.92933830226674362852985276677202 + 0.2114382218589592361562338176221i0.934115859606280075487960294154460.1904203509918773024097775641529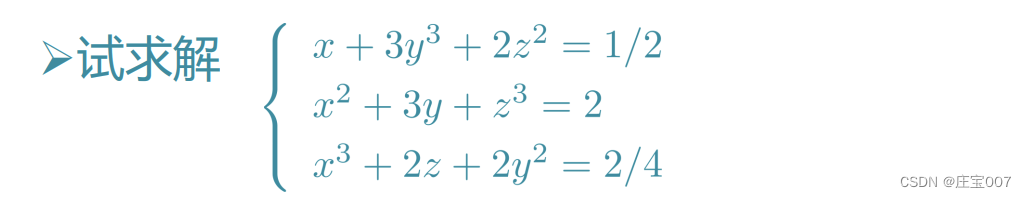
syms x y z; F=[x+3*y^3+2*z^2-1/2, x^2+3*y+z^3-2, x^3+2*z+2*y^2-2/4]; [x0,y0,z0]=vpasolve(F,[x,y,z]), size(x0)
使用了符号工具箱(Symbolic Toolbox)进行符号计算。1. `syms x y z;`: 这一行定义了符号变量 `x`、`y` 和 `z`,使它们成为符号对象,而不是普通的数值变量。这样定义的符号变量可以进行符号运算。2. `F=[......];`: 这一行定义了一个包含三个方程的方程组 `F`。每个方程都是关于 `x`、`y` 和 `z` 的符号表达式。方程组的目标是找到满足这三个方程的 `x`、`y` 和 `z` 的值。(向量型的方程解析表达式)3. `[x0,y0,z0]=vpasolve(F,[x,y,z]), size(x0)`: 这一行利用 `vpasolve` 函数求解方程组 `F`,并将解保存在变量 `x0`、`y0` 和 `z0` 中。`vpasolve` 是用于求解包含符号变量的方程组的函数。`[x0,y0,z0]` 将解分别赋给 `x0`、`y0` 和 `z0`。最后,`size(x0)` 返回解向量 `x0` 的大小,即解的个数。所以,这段代码的作用是解方程组 `F`,并返回解的个数。解向量 `x0`、`y0` 和 `z0` 包含了方程组的解。
>> norm(subs(F,{x,y,z},{x0,y0,z0}))
ans =
6.1612263763129763734660360111682e-34
计算方程组 `F` 在求解后得到的 `x0`、`y0` 和 `z0` 值处的误差向量的二范数。1. `subs(F,{x,y,z},{x0,y0,z0})`: 这一部分使用 `subs` 函数,将方程组 `F` 中的符号变量 `x`、`y` 和 `z` 替换为它们的解 `x0`、`y0` 和 `z0`,生成了一个数值的向量。这个向量代表了在解 `x0`、`y0` 和 `z0` 处,方程组的每个方程的数值结果。2. `norm(...)`: 在这里用于计算误差向量的二范数,即向量的模。综合起来,`norm(subs(F,{x,y,z},{x0,y0,z0}))` 的作用就是计算方程组 `F` 在求解后得到的 `x0`、`y0` 和 `z0` 值处的误差向量的二范数,从而衡量求解结果的精确度。

syms x y; F=[x^2/2+x+3/2+2/y+5/(2*y^2)+3/x^3; y/2+3/(2*x)+1/x^4+5*y^4]; [x0,y0]=vpasolve(F,[x,y]), size(x0)
>> norm(subs(F,{x,y},{x0,y0}))
ans =
1.7815462397351061220372854390882e-33

>> syms a b x y; [x1,y1]=solve(x^2+a*x^2+6*b+3*y^2==0,y==a+(x+3),[x,y])x1 =(4*a + 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4) - a - 3
(4*a - 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4) - a - 3y1 =(4*a + 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4)
(4*a - 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4)
相关文章:

【matlab基础知识代码】(十六)代数方程的图解法多项式型方程的准解析解方法
>> ezplot(exp(-3*t)*sin(4*t2)4*exp(-0.5*t)*cos(2*t)-0.5,[0 5]), line([0 5],[0 0]) 验证 >> t0.6738; >> exp(-3*t)*sin(4*t2)4*exp(-0.5*t)*cos(2*t)-0.5 ans -2.9852e-04 >> ezplot(x^2*exp(-x*y^2/2)exp(-x/2)*sin(x*y)) >> hold on; …...

智能奶柜:健康生活新风尚
智能奶柜:健康生活新风尚 在快节奏的都市生活中,健康与便利成为了现代人的双重追求。而在这两者交汇之处,智能奶柜应运而生,它不仅是科技与生活的完美融合,更是日常营养补给的智慧之选。 清晨的第一缕温暖 —— 新鲜…...

SpringBoot 集成 FFmpeg 解析音视频
文章目录 1 摘要2 核心 Maven 依赖3 核心代码3.1 FFmpeg 解析音视频工具类3.2 音视频文件信息参数3.3 音视频文件上传Controller3.4 application 配置文件 4 测试数据4.1 视频文件解析4.2 音频文件解析 5 注意事项5.1 文件必须在本地 6 推荐参考文档7 Github 源码 1 摘要 FFmp…...
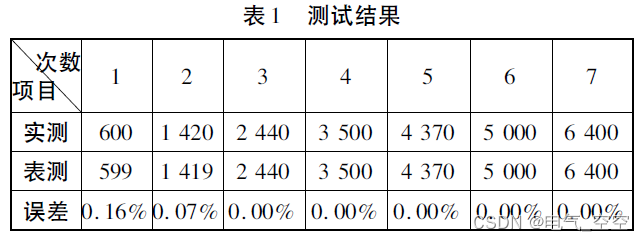
基于单片机的直流电机测速装置研究与设计
摘要: 基于单片机的直流电机测速装置采用了对直流电机的中枢供电回路串联取样电阻的方式实现对电机转速的精确实时测量。系统由滤波电路、信号放大电路、单片机控制电路以及稳压电源等功能模块电路构成。工作过程中高频磁环作为载体,利用电磁感应的基本原理对直流电…...

【快捷部署】022_ZooKeeper(3.5.8)
📣【快捷部署系列】022期信息 编号选型版本操作系统部署形式部署模式复检时间022ZooKeeper3.5.8Ubuntu 20.04tar包单机2024-05-07 一、快捷部署 #!/bin/bash ################################################################################# # 作者ÿ…...

引领AI数据标注新纪元:景联文科技为智能未来筑基
在人工智能蓬勃发展的今天,数据如同燃料,驱动着每一次技术飞跃。在这场智能革命的浪潮中,景联文科技凭借其深厚的专业实力与前瞻性的战略眼光,正站在行业前沿,为全球的人工智能企业提供坚实的数据支撑。 全国布局&…...

多模态大语言模型和 Apple 的 MM1
原文地址:multimodal-large-language-models-apples-mm1 2024 年 4 月 13 日 抽象是计算机科学中最关键的概念之一,具有一些最强大的影响。从简单的角度来看,抽象就是将某一事物应用于多种不同情况的能力。例如,如果你创造了一种…...
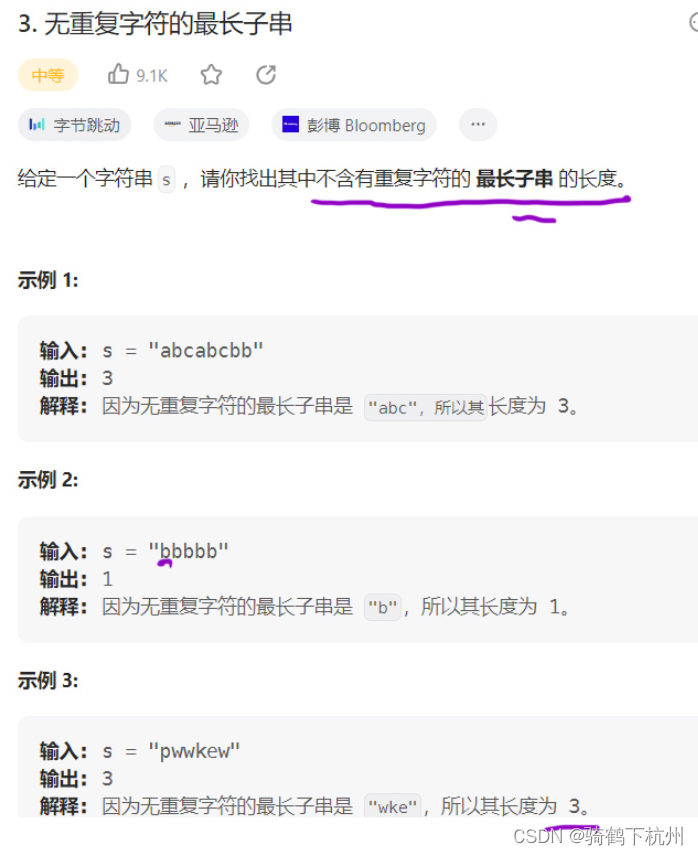
算法day04
第一题 : 209. 长度最小的子数组 有上题可知,我们会采用双指针和单调性的思路来解决 我们本题采用左右双指针从数组的0位置同向前进,所以将此类模型称为滑块; 步骤思路如下: 步骤一: 定义所有双指针都指向…...
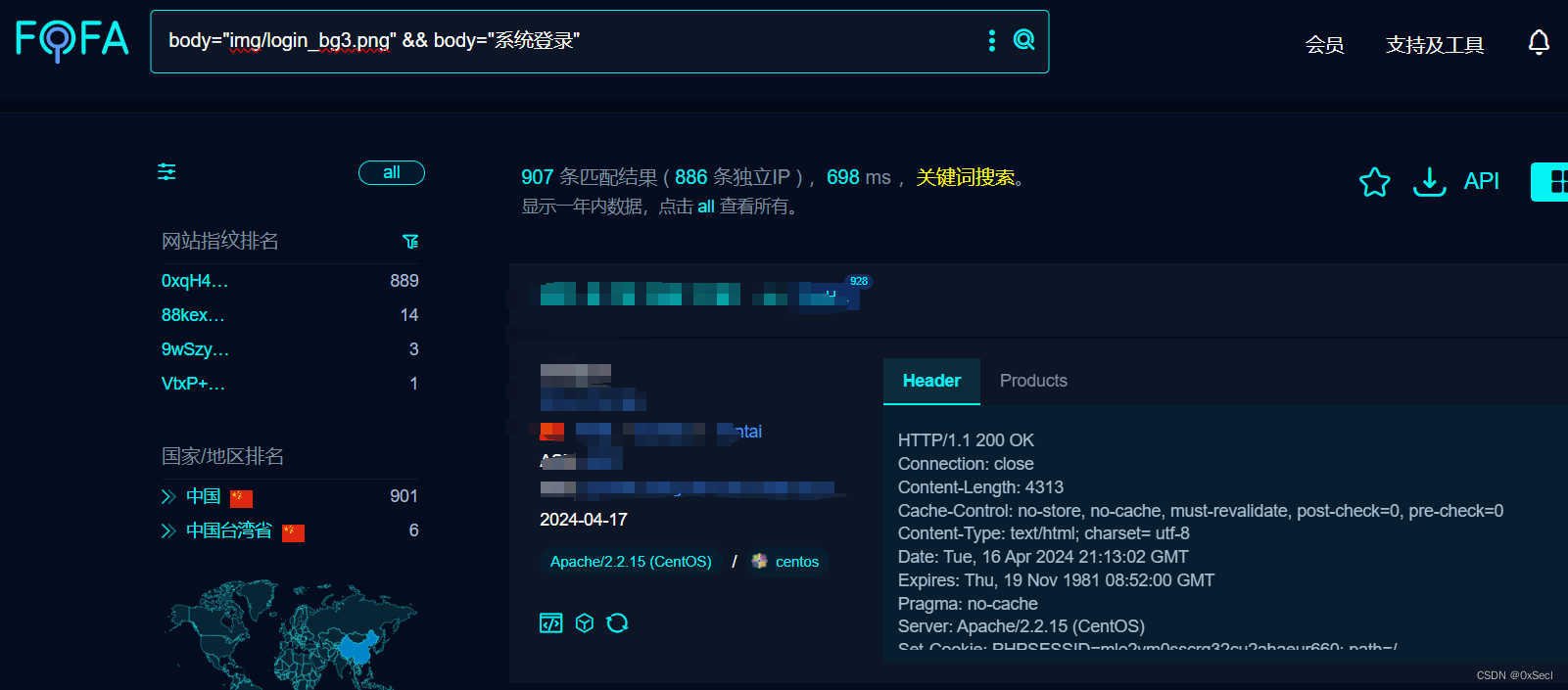
电信网关配置管理系统 rewrite.php 文件上传致RCE漏洞复现
0x01 产品简介 中国电信集团有限公司(英文名称“China Telecom”、简称“中国电信”)成立于2000年9月,是中国特大型国有通信企业、上海世博会全球合作伙伴。电信网关配置管理系统是一个用于管理和配置电信网络中网关设备的软件系统。它可以帮助网络管理员实现对网关设备的远…...

从零学算法14
14. 最长公共前缀 编写一个函数来查找字符串数组中的最长公共前缀。 如果不存在公共前缀,返回空字符串 “”。 示例 1: 输入:strs [“flower”,“flow”,“flight”] 输出:“fl” 示例 2: 输入:strs [“d…...
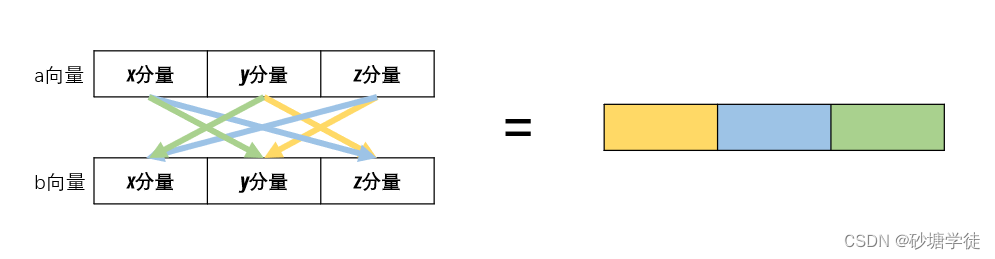
[入门] Unity Shader前置知识(5) —— 向量的运算
在Unity中,向量无处不在,我想很多人都使用过向量类的内置方法 normalized() 吧,我们都知道该方法是将其向量归一化从而作为一个方向与速度相乘,以达到角色朝任一方向移动时速度都相等的效果,但内部具体是如何将该向量进…...

html的i标签 “\e905“ font-family 字体没有效果
一、html的i标签 “\e905” 没有效果 在HTML和CSS中,\e905 这样的字符通常与字体图标(Font Icons)或自定义字体(Custom Fonts)中的Unicode字符相关。具体来说,\e905 是一个Unicode转义序列,但它…...
 的用法及示例)
Golang reflect.MakeFunc() 的用法及示例
Golang 作为一门强类型语言,在某些场景下,我们需要动态地创建函数或者修改函数,这个时候就可以使用反射的方法去实现。在反射中,我们可以使用 reflect.MakeFunc() 方法来创建一个新的函数,本文我将介绍使用反射及其 Ma…...

深入学习和理解Django视图层:处理请求与响应
title: 深入学习和理解Django视图层:处理请求与响应 date: 2024/5/4 17:47:55 updated: 2024/5/4 17:47:55 categories: 后端开发 tags: Django请求处理响应生成模板渲染表单处理中间件异常处理 第一章:Django框架概述 1.1 什么是Django?…...
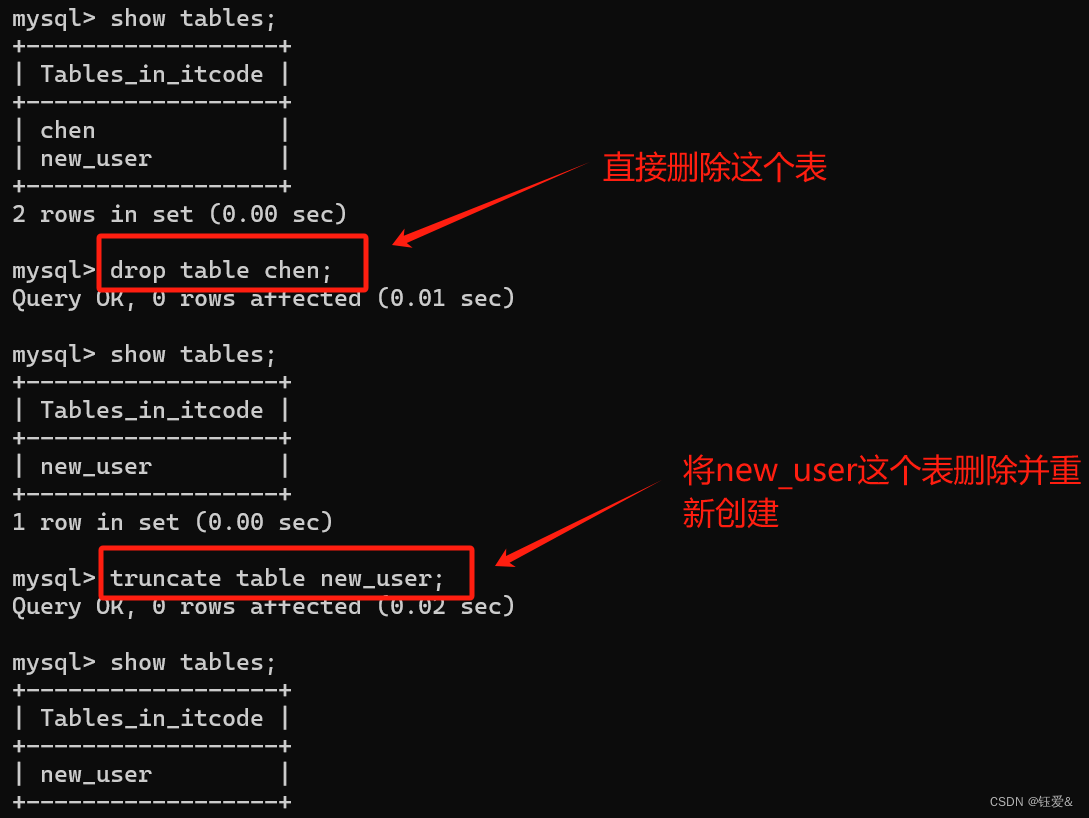
【MySQL】SQL基本知识点DDL(1)
目录 1.SQL分类: 2.DDL-数据库操作 3.DDL-表操作-创建 4.DDL-表操作-查询 5.DDL-表操作-数据类型 6.DDL-表操作-修改 1.SQL分类: 2.DDL-数据库操作 3.DDL-表操作-创建 注意:里面的符号全部要切换为英文状态 4.DDL-表操作-查询 5.DDL…...

短剧奔向小程序,流量生意如何开启?
随着移动互联网的飞速发展,小程序作为一种轻量级、易传播的应用形态,逐渐在各个领域展现出其独特的商业价值。而最近爆火的短剧小视频作为一种受众广泛的娱乐形式,与小程序结合后,不仅为观众提供了更为便捷的观看体验,…...
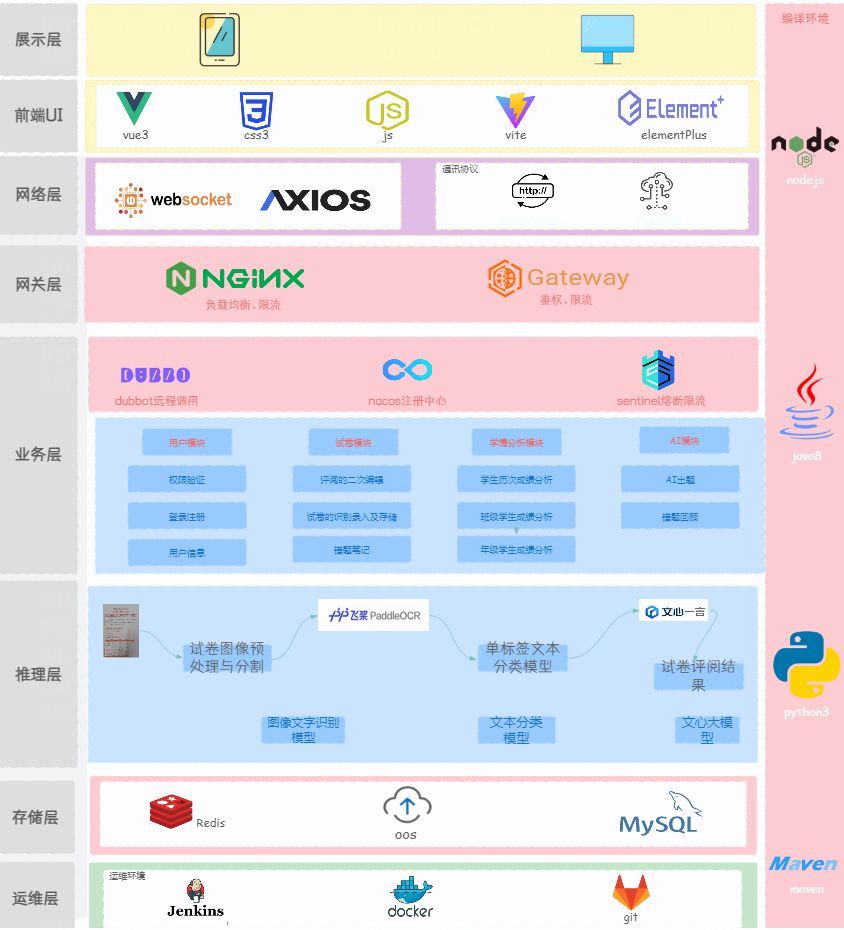
微服务下的技术栈架构解析
微服务是一种架构风格,它将一个复杂的应用拆分成多个独立自治的服务,每个服务负责应用程序中的一小部分功能。这些服务通过定义良好的API进行通信,通常是HTTP RESTful API或事件流。微服务架构的主要特点包括单一职责、自治性、可独立部署和扩…...
)
Mesa3D图形库与NIR(New Intermediate Representation)
Mesa 是一个开源图形库,为 Unix 和 Linux 系统提供了 OpenGL 和 Vulkan API 的实现。它也支持其他图形 API,如OpenCL、OpenGL ES 和 Vulkan。Mesa 项目的目标是为开源社区提供高性能的图形库,使得开源操作系统能够充分利用现代图形硬件。 Me…...
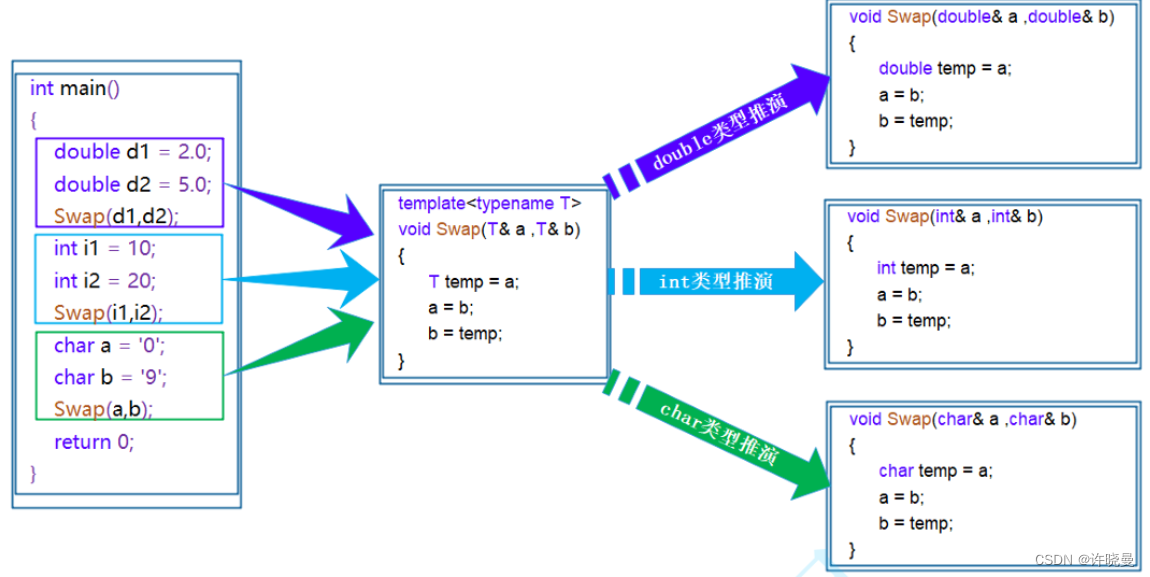
C++:模板初阶
文章目录 泛型编程函数模板概念函数模板格式函数模板的原理函数模板的实例化模板参数的匹配原则 模板类类模板的定义格式类模板实例化 泛型编程 如何实现一个通用的交换函数呢? 函数重载可以帮助我们完成 void Swap(int& left, int& right) {int temp l…...

为什么要学Python?学Python有什么用?
为什么要学Python?学Python有什么用? 在当今的数字化时代,编程已成为一项宝贵的技能。Python,作为一种流行的编程语言,因其易于学习和强大的功能而受到全球开发者的青睐。本文将探讨学习Python的原因和它的实际应用&am…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
