VBA_MF系列技术资料1-605
MF系列VBA技术资料1-605
为了让广大学员在VBA编程中有切实可行的思路及有效的提高自己的编程技巧,我参考大量的资料,并结合自己的经验总结了这份MF系列VBA技术综合资料,而且开放源码(MF04除外),其中MF01-04属于定向赠送,其余资料需要您获得三套教程后联系获得。每位学员可获得的数量与您拥有教程数相关,但如果您获得了我的全部九套教程+手册+NZ,YZ工具(即:T3资格学员),这个系列资料您可以全部获得。如果您还不是我的学员,您可以选择分享(MF01-MF04除外)。目前这个系列资料一共为605份,以后还会源源不断的推出。















【分享成果,随喜正能量】
相关文章:

VBA_MF系列技术资料1-605
MF系列VBA技术资料1-605 为了让广大学员在VBA编程中有切实可行的思路及有效的提高自己的编程技巧,我参考大量的资料,并结合自己的经验总结了这份MF系列VBA技术综合资料,而且开放源码(MF04除外),其中MF01-0…...

算法题① —— 数组专栏
1. 滑动窗口 1.1 长度最小的子数组 力扣:https://leetcode.cn/problems/minimum-size-subarray-sum/description/ int minSubArrayLen(int s, vector<int>& nums) {int result INT32_MAX; int sum 0; // 子序列的数值之和int subLength 0; // 子序列…...
)
算法学习笔记(差分约束系统)
前置:spfa 从例题入手: 【模板】差分约束系统 | StarryCoding 题目描述 给定 n n n未知量和一个大小为 m m m的不等式(或等式)组,请你判断这个不等式(或等式)组是否有解。 1 1 1 i i i j …...

HCIP的学习(14)
过滤策略—filter-policy 思科中:分发列表 过滤策略是只能够针对于路由信息进行筛选(过滤)的工具,而无法针对于LSA进行过滤。 在R4的出方向上配置过滤策略,使得R1不能学习到23.0.0.0/24路由信息1、抓取流量 […...

行业新应用:电机驱动将成为机器人的动力核心
电机已经遍布当今社会人们生活的方方面面,不仅应用范围越来越广,更新换代的速度也日益加快。按照工作电源分类,可以将它划分为直流电机和交流电机两大类型。直流电机中,按照线圈类型分类,又可以分为有铁芯的电机、空心…...

大模型模型简化机器人训练;简单易用的 3D 工具Project Neo;特斯拉放出了擎天柱机器人最新训练视频
✨ 1: DrEureka 利用大语言模型自动化将机器人仿真环境训练结果转移到真实世界 DrEureka是一种利用大型语言模型(LLMs)自动化和加速从仿真(sim)到现实世界(real)转移的技术。在机器人技能学习领域&#x…...
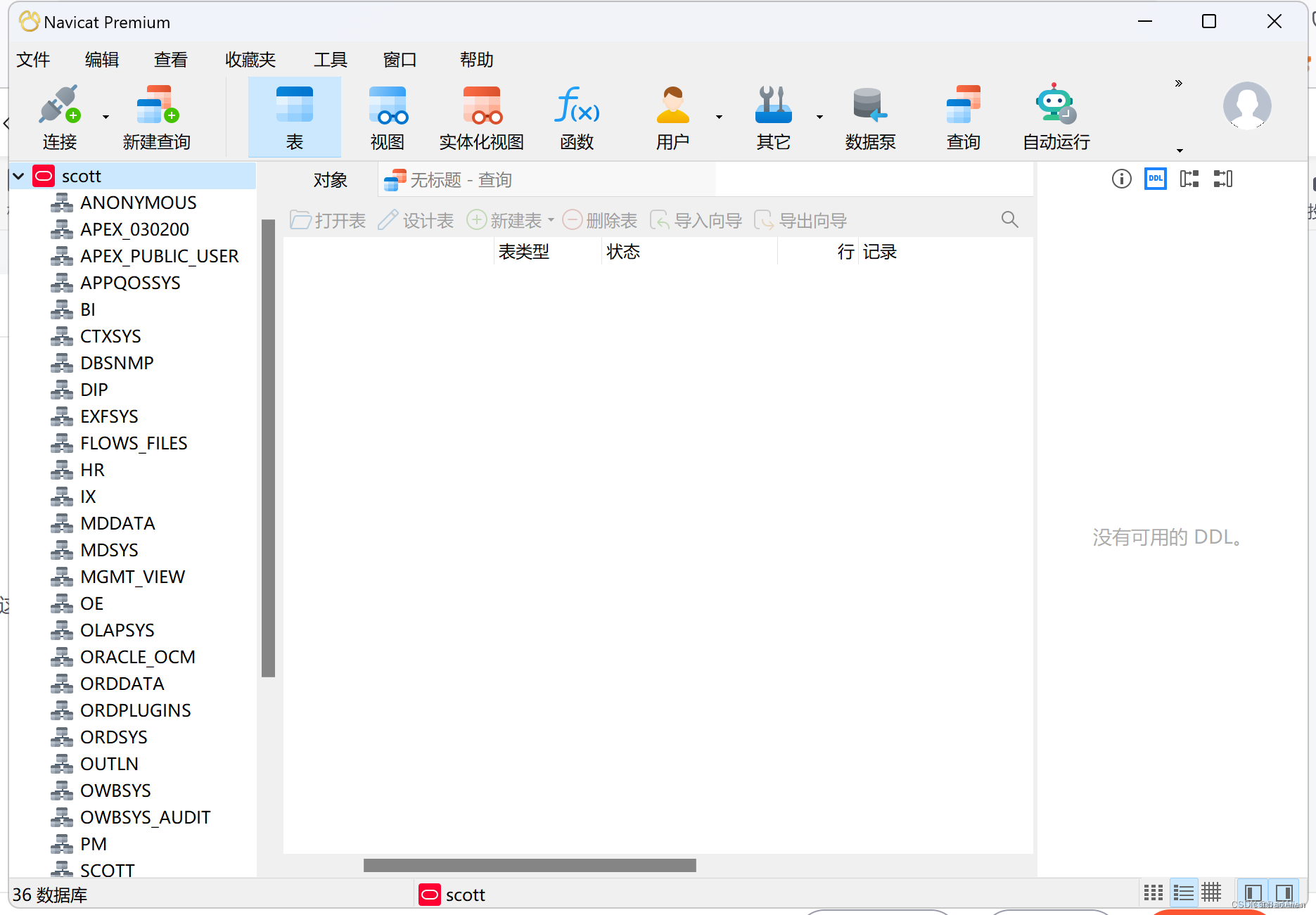
Win11安装Docker Desktop运行Oracle 11g 【详细版】
oracle docker版本安装教程 步骤拉取镜像运行镜像进入数据库配置连接数据库,修改密码Navicat连接数据库 步骤 拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/helowin/oracle_11g运行镜像 docker run -d -p 1521:1521 --name oracle11g registry.cn-ha…...
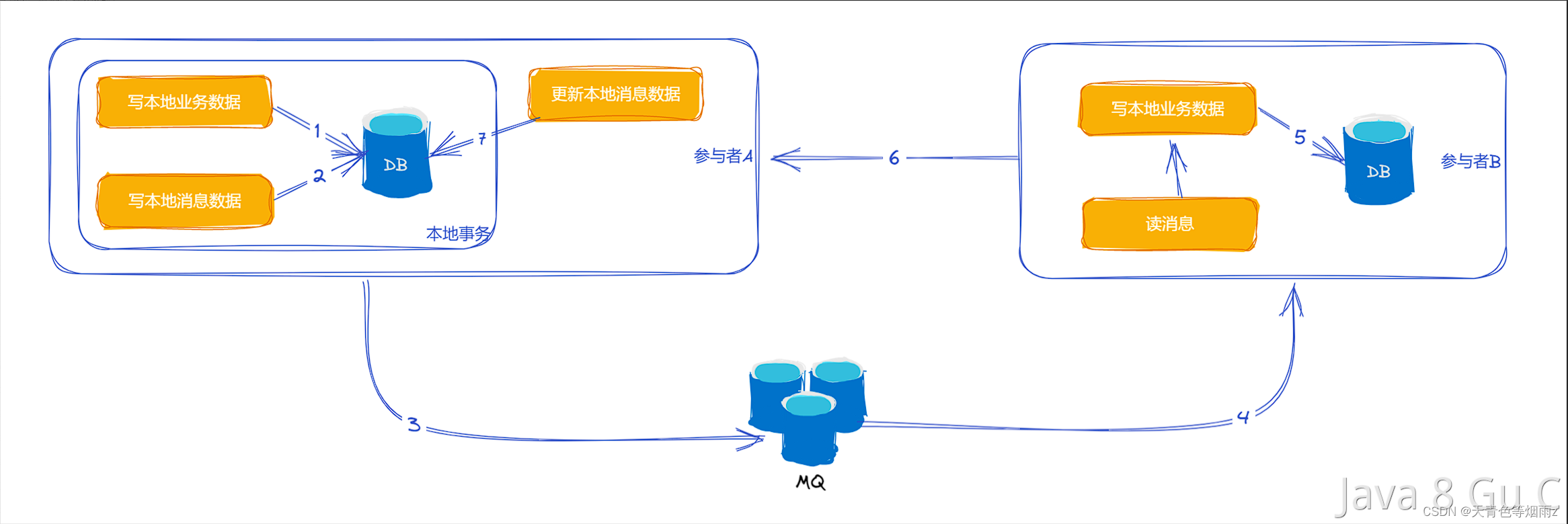
分布式事务?哪几种方式实现?一文看懂!
什么是分布式事务 分布式事务是指在分布式系统中涉及到多个数据库或多个应用程序之间的事务处理,这些数据库或应用程序可能分布在不同的物理节点上,甚至可能位于不同的地理位置。在分布式事务中,需要确保所有参与者的事务操作都能够保持一致性…...
词令蚂蚁庄园今日答案如何在微信小程序查看蚂蚁庄园今天问题的正确答案?
词令蚂蚁庄园今日答案如何在微信小程序查看蚂蚁庄园今天问题的正确答案? 1、打开微信,点击搜索框; 2、打开搜索页面,选择小程序搜索; 3、在搜索框,输入词令搜索点击进入词令微信小程序; 4、打开…...

【Delphi 爬虫库 6】使用正则表达式提取猫眼电影排行榜top100
正则表达式库的简单介绍 正则表达式易于使用,功能强大,可用于复杂的搜索和替换以及基于模板的文本检查。这对于输入形式的用户输入验证特别有用-验证电子邮件地址等。您还可以从网页或文档中提取电话号码,邮政编码等,在日志文件中…...

Markdown和Latex中文字上下标的方法
技术背景 在Markdown和Latex中,如果只是写公式,不论是行内公式还是行间公式,都可以直接使用^和_这两个符号实现上下标。但有个问题是,如果只是使用公式来做上下标,出来的字体是斜着的。例如这样的语法: $$ …...
VSCode:设置顶部文件标签页滚动条的宽度
使用VSCode打开多个文件后,顶部的文件标签可以通过滚动条进行滚动,但是缺点是该滚动条太窄了,不好选择。 可以通过如下方法修改改滚动条的宽度: 1.点击设置 2.选择工作台->编辑管理->Title Scrollbar Sizing->Large 3.可…...

MySQL变量的定义与使用
# 关系运算 select x < y as 大小判断;# 返回结果1代表true,如果是0代表false select x > y; # 逻辑运算 select TRUE and FALSE;# 依然符合&(and)与、|(or)或、^(xor)亦或。 select …...

python-pytorch seq2seq+attention笔记0.5.00
python-pytorch seq2seq+attention笔记0.5.00 1. LSTM模型的数据size2. 关于LSTM的输入数据包含hn和cn时,hn和cn的size3. LSTM参数中默认batch_first4. Attention机制的三种算法5. 模型的编码器6. 模型的解码器7. 最终模型8. 数据的准备9. 遇到的问题10. 完整代码1. LSTM模型的…...

ansible 深入介绍之 主机清单与playbook
目录 一 inventory 主机清单 1,主机清单 是什么 2,主机清单 定义方式 2.1 自定义主机端口 2.2 定义 范围ip 地址 2.3 定义 拥有相似的主机名 3, inventory 中的变量 3.1 常见 变量 3.2 主机变量 3.3 组变量 3.…...

【MySQ】9.构建高可用数据库:MySQL集群模式部署大全
单个MySQL节点的主要风险在于它构成了一个单点故障,这意味着任何硬件故障、软件崩溃或维护需求都可能导致整个数据库服务中断,从而影响到业务的连续性和数据的安全性。此外,它还限制了系统的扩展性,使得性能提升和负载均衡变得困难…...
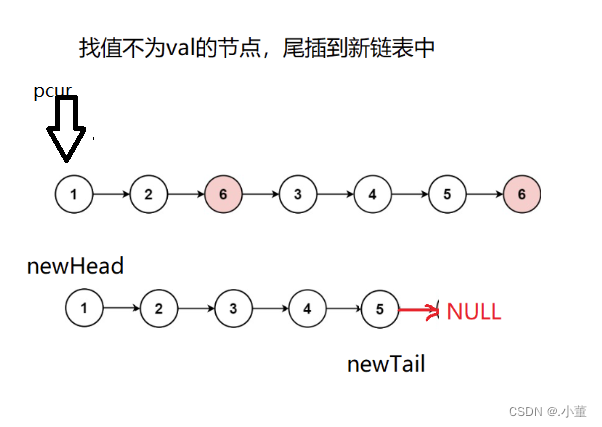
Leedcode题目:移除链表元素
题目: 这个题目就是要我们将我们的链表中的值是val的节点删除。 我们题目提供的接口是 传入了指向一个链表的第一个节点的指针,和我们要删除的元素的值val,不只要删除第一个, 思路 我们这里可以创建一个新的链表,…...

1_1. Linux简介
1_1. Linux简介 文章目录 1_1. Linux简介1. 我们用linux来干嘛2. 计算机组成3. 操作系统4. Linux哲学思想5. Linux目录6. Linux分区类型 1. 我们用linux来干嘛 1. 大家都知道linux是一个操作系统,它是一个基础的软件,操作系统是硬件与应用程序的中间层。…...

Swift 函数
函数 一、函数的定义与调用二、函数参数与返回值1、无参数函数2、多参数函数3、无返回值函数4、多重返回值函数5、可选元组返回类型6、隐式返回的函数 三、函数参数标签和参数名称1、指定参数标签2、忽略参数标签3、默认参数值4、可变参数5、输入输出参数 四、函数类型1、使用函…...
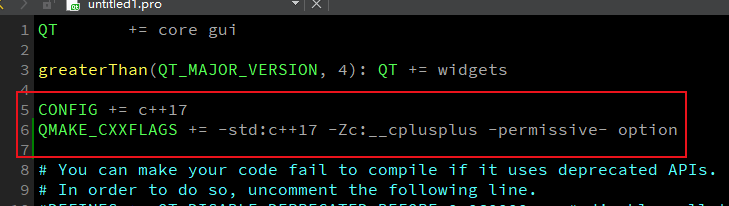
QT creator qt6.0 使用msvc2019 64bit编译报错
qt creator qt6.0报错: D:\Qt6\6.3.0\msvc2019_64\include\QtCore\qglobal.h:123: error: C1189: #error: "Qt requires a C17 compiler, and a suitable value for __cplusplus. On MSVC, you must pass the /Zc:__cplusplus option to the compiler."…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
