笔试强训未触及题目(个人向)
1.DP22 最长回文子序列
1.题目

2.解析
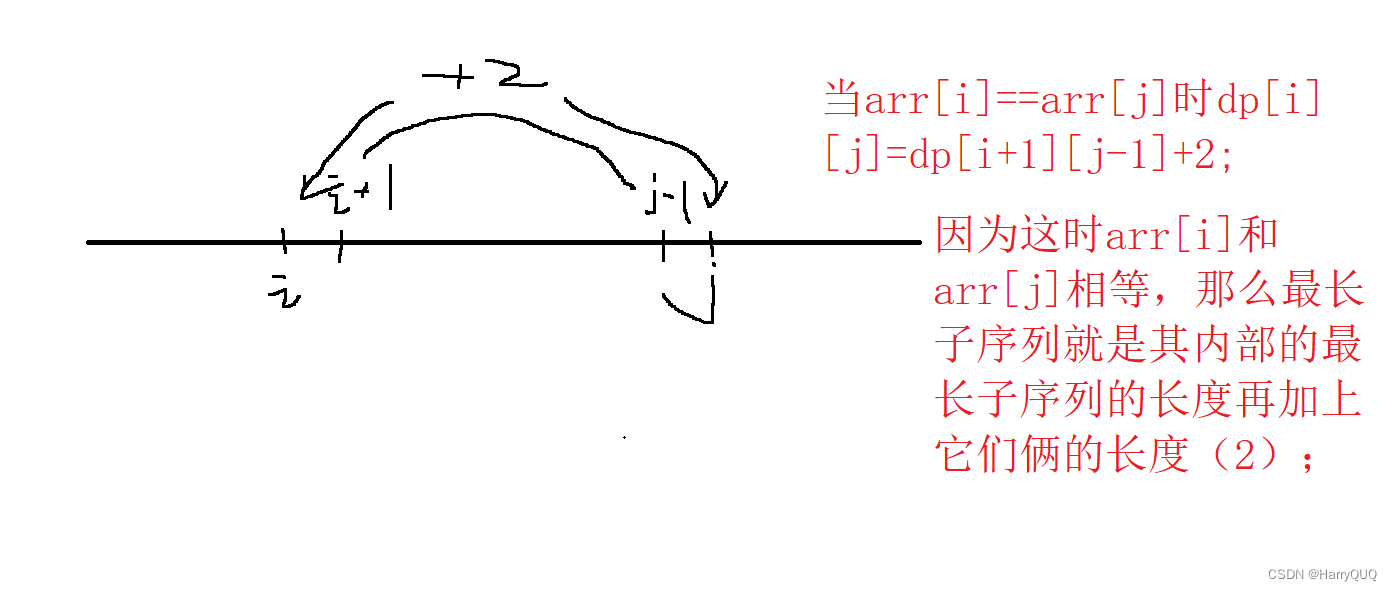
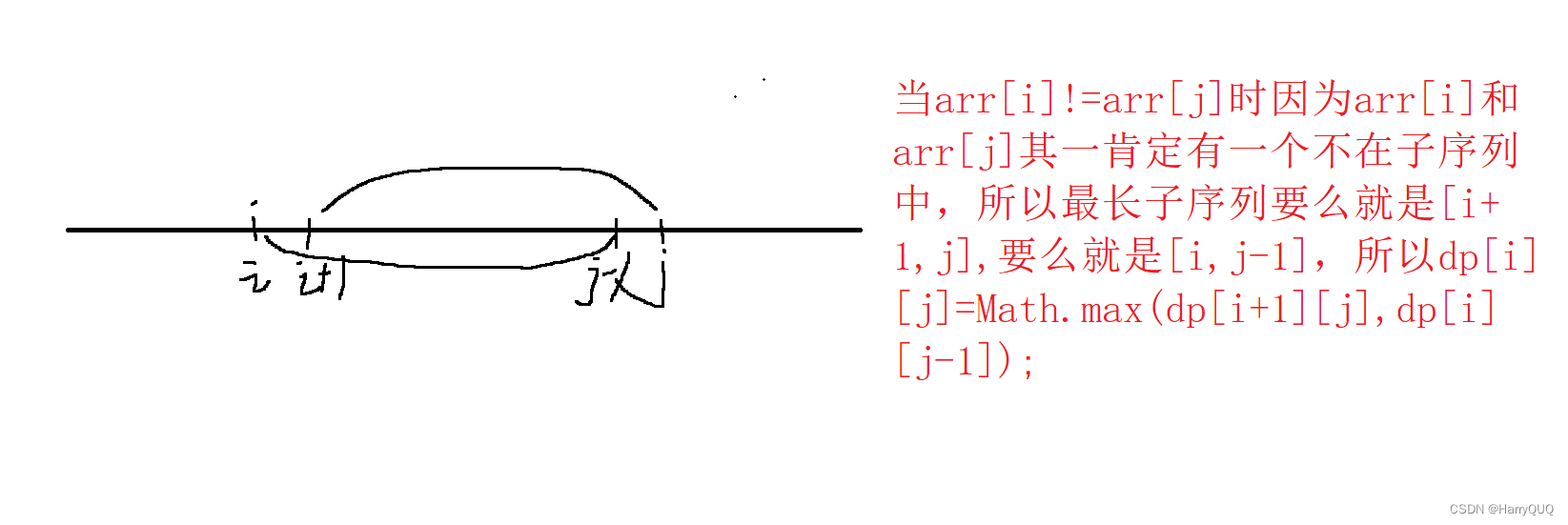
这是一个区间dp问题,我们让dp[i][j]表示在区间[i,j]内的最长子序列长度,如图:
3.代码
public class LongestArr {//DP22 最长回文子序列public static void main(String[] args) {Scanner in = new Scanner(System.in);char[] arr = in.next().toCharArray();//让dp[i][j]表示在区间i,j内的最长子序列长度//dp[i][j]=当arr[i]==arr[j]时为dp[i+1][j-1]+2;//当arr[i]!=arr[j]时因为arr[i]和arr[j]其一肯定//有一个不在子序列中,所以dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);int n = arr.length;int[][] dp = new int[n][n];//初始化,当i=j时为1,i>j时为0(因为长度为负数不能算有字符串,i<j时要计算,最后取dp[0][n-1])for (int i = n - 1; i >= 0; i--) {for (int j = i; j < n; j++) {if (j == i) {dp[i][j] = 1;} else {if (arr[i] == arr[j]) {dp[i][j] = dp[i + 1][j - 1] + 2;} else {dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);}}}}System.out.print(dp[0][n - 1]);}
}2.数组变换
1.题目


2.解析

那么综上所述我们只要知道最大的数是否能和其他数匹配就行,但是问题来了,怎么知道它们是否匹配呢。我们可以先让最大数除以另一个想要与之匹配的数,若除不尽,则不能匹配,若除尽,则判断商是否为2的n次方。这里除尽除不尽用%小数来表示。那怎么判断是否为2的n次方呢,这里有三种方式,一种是暴力求法,让这个数无限/2,%2即可,第二种是lowbit算法,判断x-(x&-x)是否为0,第三种就是之前做过的判断1的位数的位运算方法,因为我们只需要判断是否只有1位1,所以,判断x&(x-1)是否为0即可。下文采用的是lowbit算法。
3.代码
public class demo2 {//数组变换public static void main(String[] args) {Scanner in = new Scanner(System.in);//取最大的数和其余的数做比较,看这个数能否变成这个最大的数//输入时判断最大数int n = in.nextInt();int max = 0;int[] arr = new int[n];for (int i = 0; i < n; i++) {int tem = in.nextInt();if (i == 0) {max = tem;} else max = Math.max(tem, max);arr[i] = tem;}for (int i = 0; i < n; i++) {//判断能否变为最大的数if (max % arr[i] == 0) {int s = max / arr[i];if (s - (s & -s) != 0) {System.out.print("NO");return;}} else {System.out.print("NO");return;}}System.out.print("YES");}
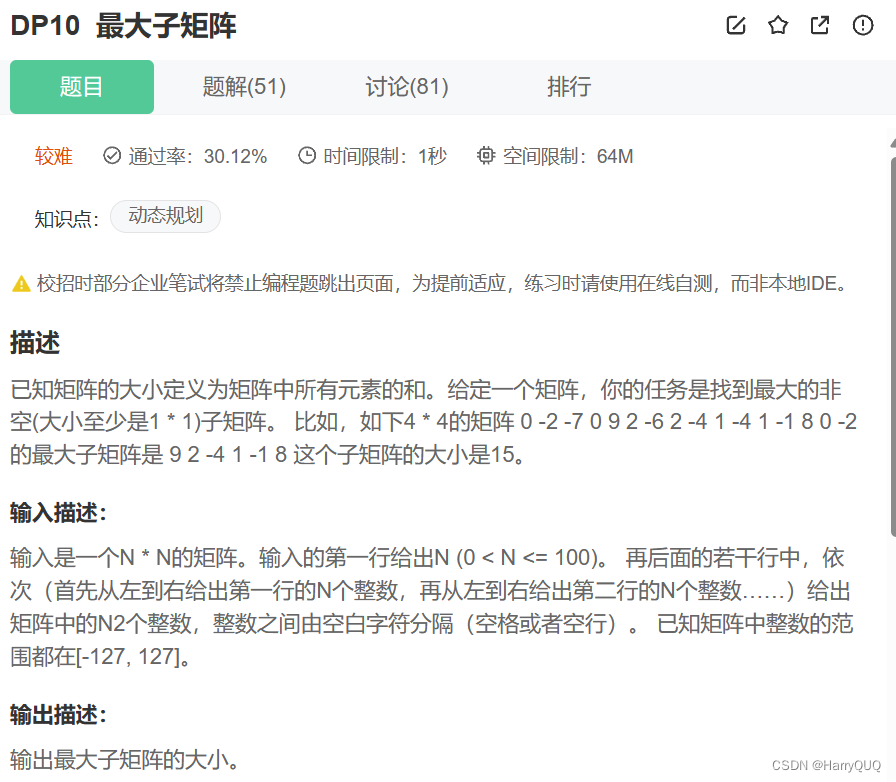
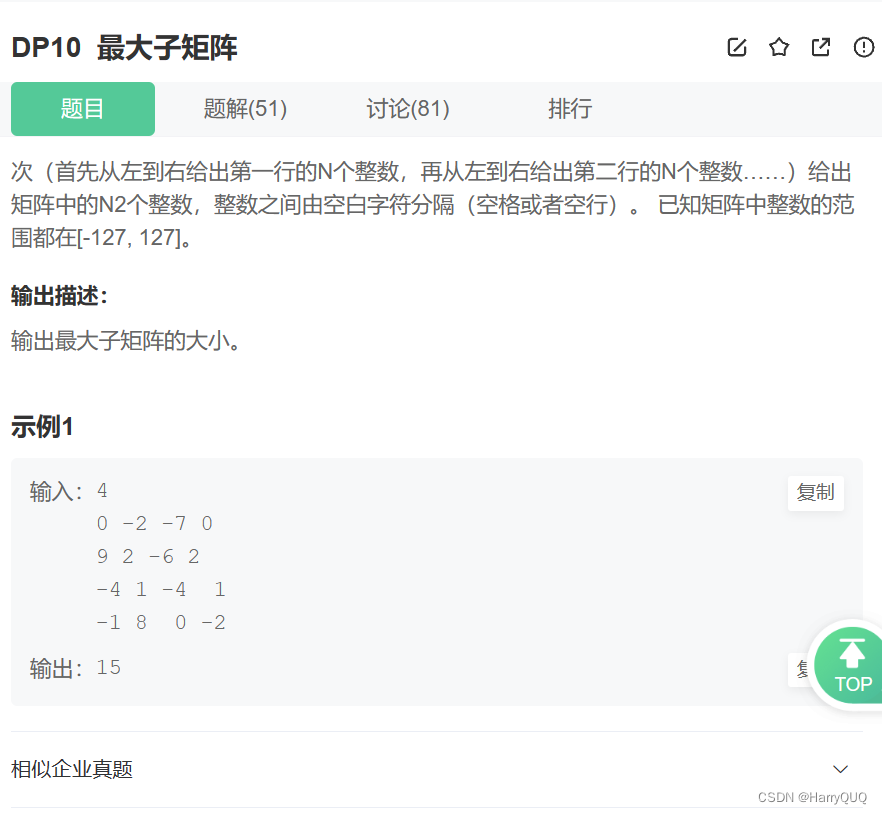
}3.DP10 最大子矩阵
1.题目
2.解析
在判断矩阵最大大小之前,我们肯定要枚举所有矩阵,如图:

for(int x1=0;x1<n;x1++) {for(int y1=0;y1<n;y1++) {for(int x2=x1;x2<n;x2++) {for(int y2=y1;y2<n;y2++) {//这里写判断大小的一系列逻辑 }}}我们要计算矩阵内部的和,有两种方法,一种是暴力解法,用两层for循环来一个一个加起来,但是这样时间复杂度就是O(n^2)加上外部循环就是 O(n^6)。所以我们用第二种方法,前缀和如图:
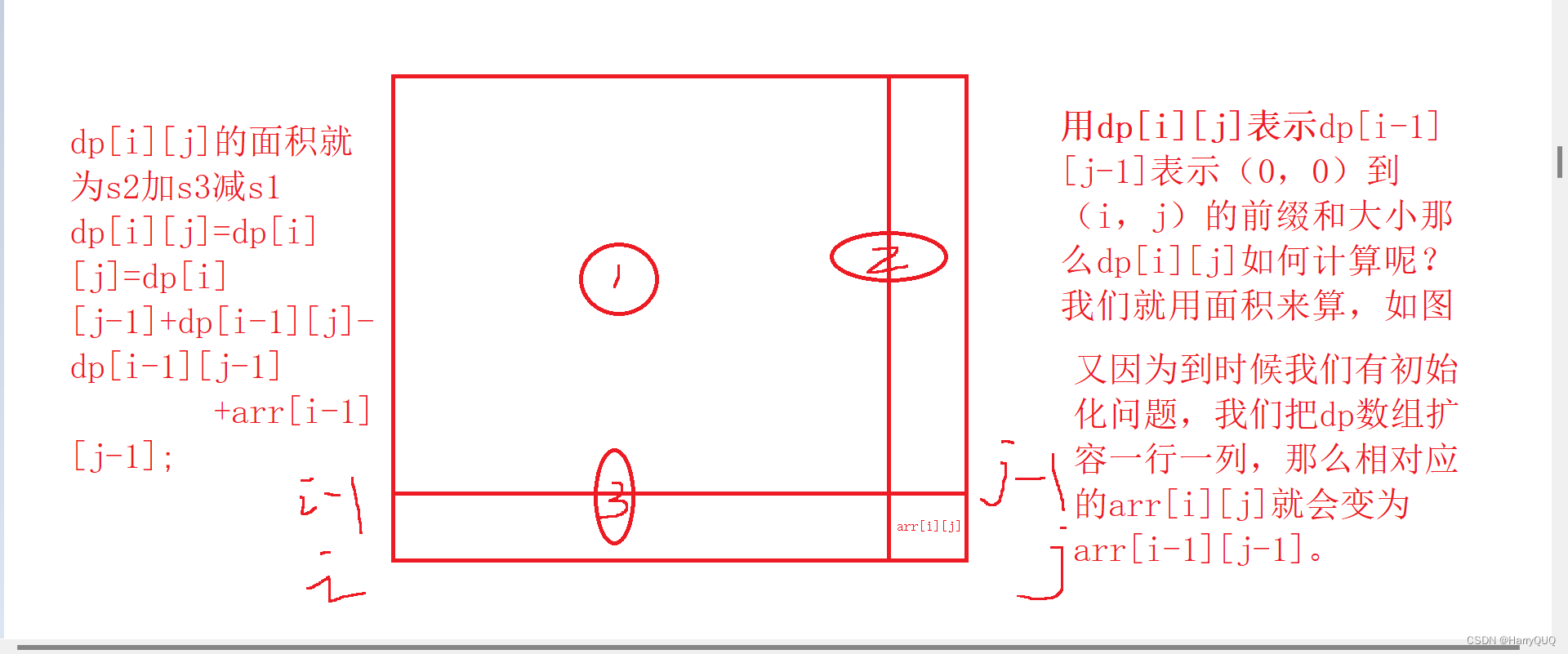
那么如何使用呢?如图:
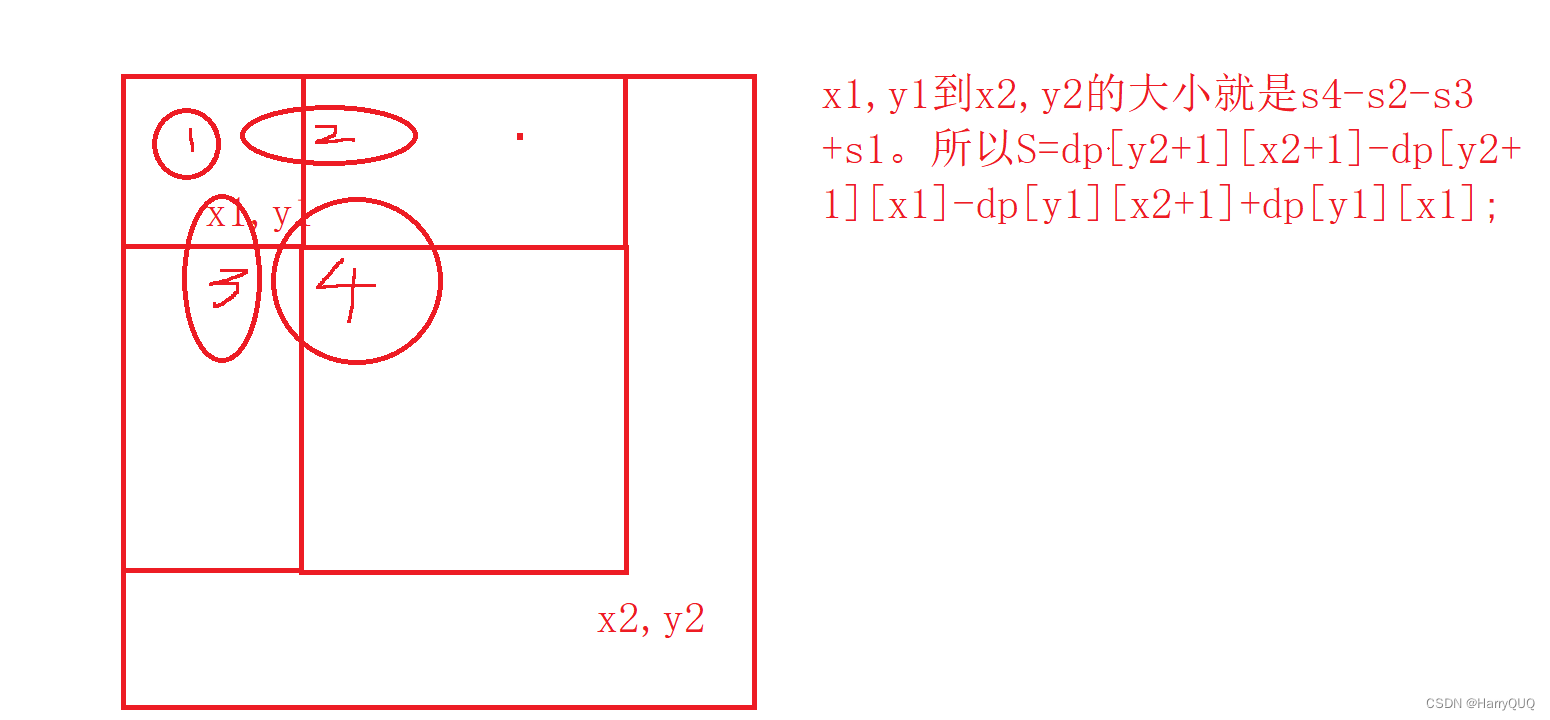
最后比较最大值就行
3.代码
public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();//输入数据int[][] arr=new int[n][n];for(int i=0;i<n;i++) {for(int j=0;j<n;j++) {arr[i][j]=in.nextInt();}}//用二维dp计算前缀和//dp[i-1][j-1]表示(0,0)到(i,j)的前缀和大小//初始化int[][] dp=new int[n+1][n+1];for(int i=1;i<=n;i++) {for(int j=1;j<=n;j++) {dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+arr[i-1][j-1];}}//枚举每一块矩阵int max=-0x3f3f3f3f;for(int x1=0;x1<n;x1++) {for(int y1=0;y1<n;y1++) {for(int x2=x1;x2<n;x2++) {for(int y2=y1;y2<n;y2++) {int tem=dp[y2+1][x2+1]-dp[y2+1][x1]-dp[y1][x2+1]+dp[y1][x1];if(max<tem) {max=tem;}}}}}System.out.print(max);}相关文章:

笔试强训未触及题目(个人向)
1.DP22 最长回文子序列 1.题目 2.解析 这是一个区间dp问题,我们让dp[i][j]表示在区间[i,j]内的最长子序列长度,如图: 3.代码 public class LongestArr {//DP22 最长回文子序列public static void main(String[] args) {Scanner…...
)
【YOLO改进】换遍MMDET主干网络之EfficientNet(基于MMYOLO)
EfficientNet EfficientNet是Google在2019年提出的一种新型卷积神经网络架构,其设计初衷是在保证模型性能的同时,尽可能地降低模型的复杂性和计算需求。EfficientNet的核心思想是通过均衡地调整网络的深度(层数)、宽度࿰…...

uniapp下拉选择组件
uniapp下拉选择组件 背景实现思路代码实现配置项使用尾巴 背景 最近遇到一个这样的需求,在输入框中输入关键字,通过接口查询到结果之后,以下拉框列表形式展现供用户选择。查询了下uni-app官网和项目中使用的uv-ui库,没找到符合条…...

高斯数据库创建函数的语法
CREATE FUNCTION 语法格式 •兼容PostgreSQL风格的创建自定义函数语法。 CREATE [ OR REPLACE ] FUNCTION function_name ( [ { argname [ argmode ] argtype [ { DEFAULT | : | } expression ]} [, …] ] ) [ RETURNS rettype [ DETERMINISTIC ] | RETURNS TABLE ( { column_…...

【.NET Core】你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟
你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟 文章目录 你认识Attribute之CallerMemberName、CallerFilePath、CallerLineNumber三兄弟一、概述二、CallerMemberNameAttribute类三、CallerFilePathAttribute 类四、CallerLineNumberAttribute 类…...

ubuntu删除opencv
要完全删除OpenCV 3.4.5版本,你可以按照以下步骤进行操作: 卸载OpenCV库: 首先,你需要卸载OpenCV 3.4.5版本。可以使用以下命令卸载OpenCV库: sudo apt-get purge libopencv*这将删除OpenCV库及其相关文件。 删除O…...
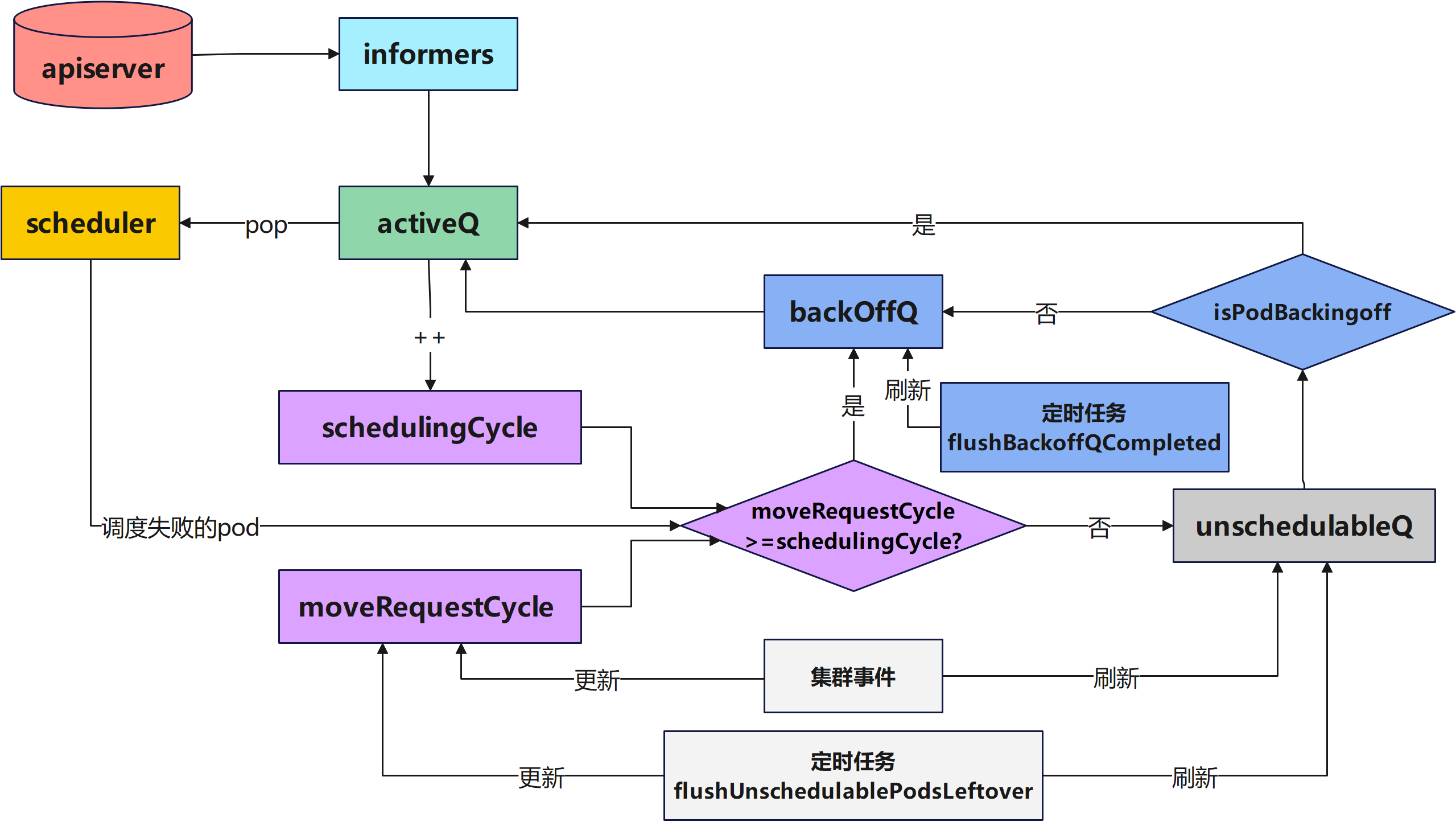
K8s源码分析(二)-K8s调度队列介绍
本文首发在个人博客上,欢迎来踩! 本次分析参考的K8s版本是 文章目录 调度队列简介调度队列源代码分析队列初始化QueuedPodInfo元素介绍ActiveQ源代码介绍UnschedulableQ源代码介绍**BackoffQ**源代码介绍队列弹出待调度的Pod队列增加新的待调度的Podpod调…...
)
OpenGL ES 面试高频知识点(二)
说说纹理常用的采样方式? 最邻近点采样(GL_NEAREST)和双线性采样(GL_LINEAR)。 GL_NEAREST 采样是 OpenGL 默认的纹理采样方式,OpenGL 会选择中心点最接近纹理坐标的那个像素,纹理放大的时候会有锯齿感或者颗粒感。 **GL_LINEAR 采样会基于纹理坐标附近的纹理像素,计…...

2024第十六届“中国电机工程学会杯”数学建模A题B题思路分析
文章目录 1 赛题思路2 比赛日期和时间3 竞赛信息4 建模常见问题类型4.1 分类问题4.2 优化问题4.3 预测问题4.4 评价问题 5 建模资料 1 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 2 比赛日期和时间 报名截止时间:2024…...

面向对象的三大特性:封装、继承、多态
一、封装 封装是面向对象的核心思想。是以类为载体,将对象的属性和行为封装起来,对外隐藏其实现细节。 封装保证了类内部数据结构的完整性,使得外部(使用该类的用户)不能轻易地直接操作此数据结构,只能执…...
)
目标检测YOLO实战应用案例100讲-基于深度学习的交通场景多尺度目标检测算法研究与应用(中)
目录 3.4 实验结果与分析 深度融合注意力跨尺度复合空洞残差交通目标检测算法...

前端GET请求下载后端返回数据流文件,并且处理window.open方法跳转白屏方法
平时常用导出都是用window.open方法 点击跳转连接:使用 window.open 下载 const downError 地址?&参数${参数|| }; const downError Url/xxx/xxx?&orgId${orgId || };window.open(downError, "_self");//调用window.open方法导出 而使用…...

SD321放大器3V输入电流电压保护二极管25C电源电流
Sd 321运算放大器可以在单电源或双电源电压下工作, 可以使用最坏情况下的非反相单位增益连接来适应。如 具有真微分输入,并且保持在线性模式,输入共模电压 果放大器必须驱动较大的负载电容,则应使用较大的闭 为0。Vpc-这种放大器可…...

geoserver SQL注入、Think PHP5 SQL注入、spring命令注入
文章目录 一、geoserver SQL注入CVE-2023-25157二、Think PHP5 SQL注入三、Spring Cloud Function SpEL表达式命令注入(CVE-2022-22963) 一、geoserver SQL注入CVE-2023-25157 介绍:GeoServer是一个开源的地理信息系统(GIS&#…...

scrapy的入门
今天我们先学习一下scrapy的入门,Scrapy是一个快速的高层次的网页爬取和网页抓取框架,用于爬取网站并从页面中提取结构化的数据。 1. scrapy的概念和流程 1.1 scrapy的概念 我们先来了解一下scrapy的概念,什么是scrapy: Scrapy是一个Python编写的开源网络爬虫框架…...
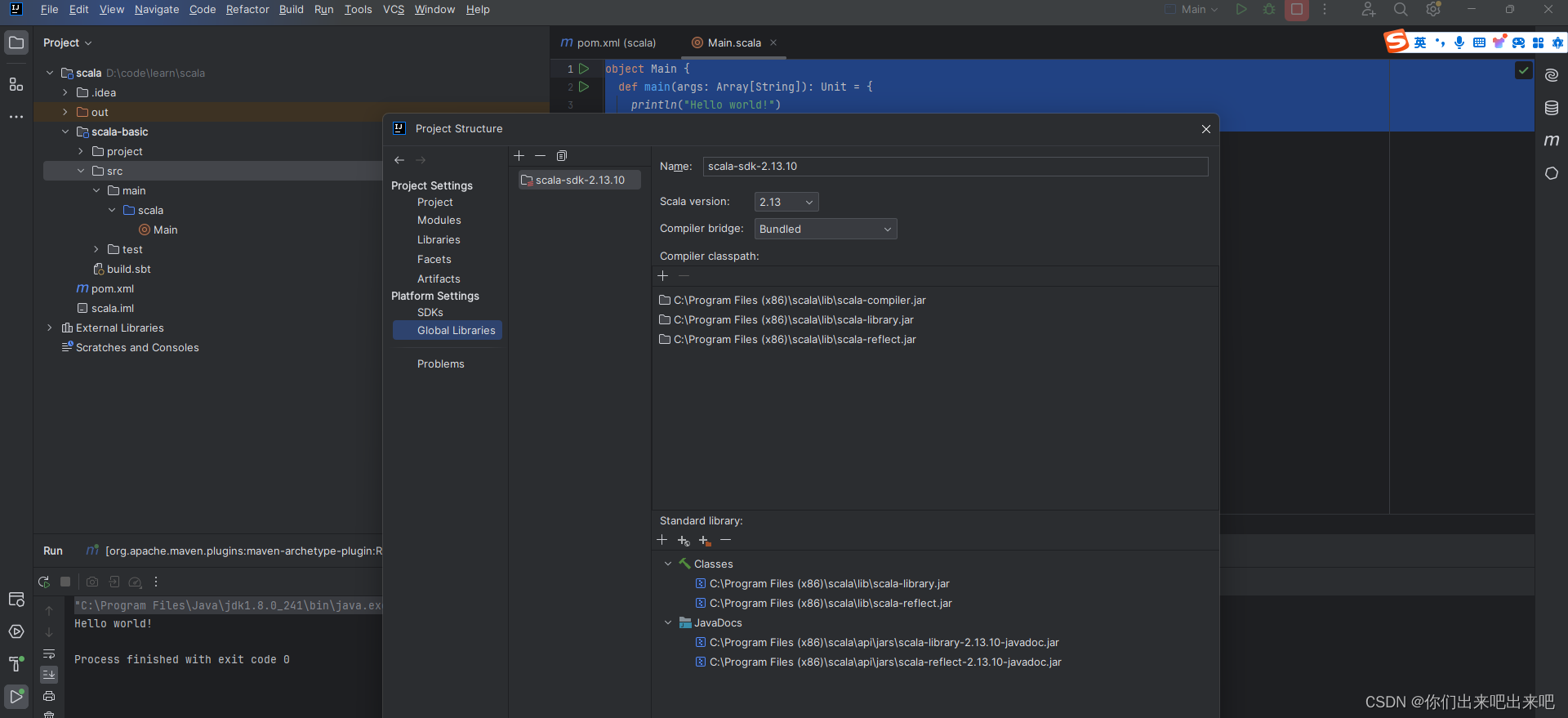
大数据Scala教程从入门到精通第七篇:Scala在IDEA中编写Hello World
一:Scala在IDEA中编写Hello World 想让我们的idea支持scala的编写,需要安装一个插件。...

设计模式之数据访问对象模式
在Java编程的浩瀚星海中,有一个模式低调却强大,它像是一位默默无闻的超级英雄,支撑起无数应用的数据脊梁——那就是数据访问对象(DAO, Data Access Object)模式!想象一下,如果你能像操纵魔法一样…...

Spring aop切面编程
Spring aop切面编程 如何使用利用AuditAction创建切入点 如何使用 Aspect // 1. 创建一个类,用Aspect注解标记它,表明这是一个切面类。 Component public class LoggingAspect {// 2. 定义切点:在通知方法上,使用切点表达式来指定…...
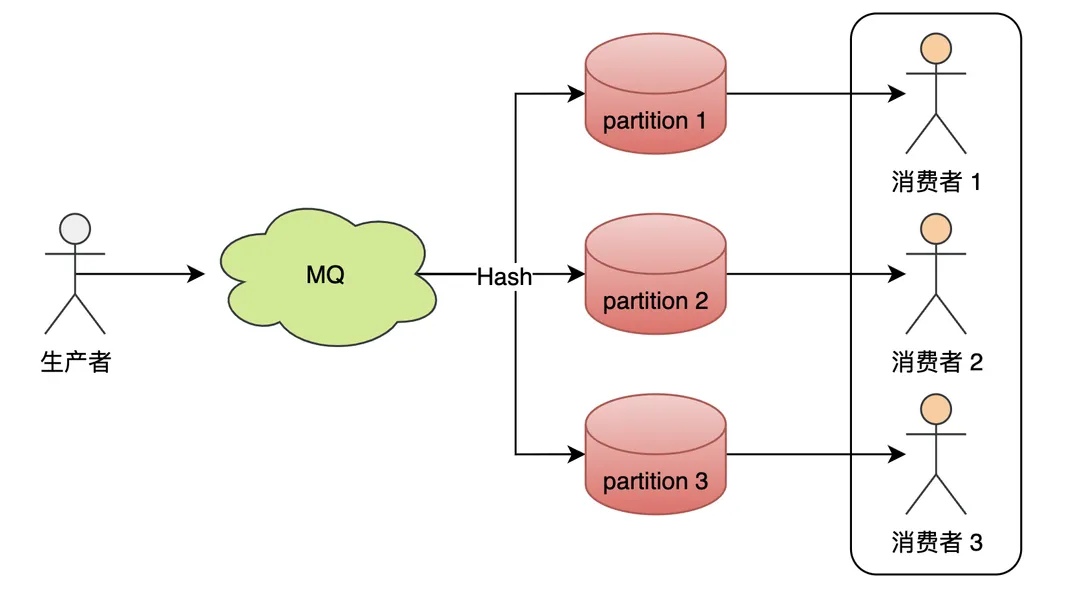
如何更好地使用Kafka? - 事先预防篇
要确保Kafka在使用过程中的稳定性,需要从kafka在业务中的使用周期进行依次保障。主要可以分为:事先预防(通过规范的使用、开发,预防问题产生)、运行时监控(保障集群稳定,出问题能及时发现&#…...

如何解决 IPA 打包过程中的 “Invalid Bundle Structure“ 错误
哈喽,大家好呀,淼淼又来和大家见面啦,咱们行业内的应该都知道,在开发 iOS 应用时,将应用打包成 IPA 文件是常见的步骤之一。最近很多小伙伴们说在打包过程中,有时会遇到 "Invalid Bundle Structure&qu…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
