2010年认证杯SPSSPRO杯数学建模D题(第一阶段)服务网点的分布全过程文档及程序
2010年认证杯SPSSPRO杯数学建模
D题 服务网点的分布
原题再现:
服务网点、通讯基站的设置,都存在如何设置较少的站点,获得较大效益的问题。通讯基站的覆盖范围一般是圆形的,而消防、快餐、快递服务则受到道路情况和到达时间的限制。现在我们将问题简化。假设城市道路构成一个 n × n 的正方形网格,交叉点称为节点,相邻节点的距离等于 1。服务站设置在某个节点上,只能沿着道路对节点服务,并且最大服务距离为 2。
第一阶段问题:
(1) 服务网点设置太多或位置不合理,可能出现多个服务点都能为同一个节点服务的现象,造成浪费;服务网点设置太少或位置不合理,可能有一些节点得不到服务。现在要求每个节点都能得到服务,而服务站点最少,请给出服务站点的设置方案,并对 n = 100, 101, 102 三种情况求出最少的服务站点数。
(2) 假设服务站是快餐派送网点,在不考虑货源成本的前提下,请问需要知道哪些数据来确定服务站点的设置方案,并建立合理的模型,给出使利润最大化的设置方法。
整体求解过程概述(摘要)
我们知道,服务网点的分布对公司企业有很大的作用。人们都想以最少的投入获取最大的利益。但是,单单是从服务网点的分布上看,要做到这一点也并不容易。本文探讨的就是在一定的服务距离内如何能以最少的服务站覆盖最多的节点,却又不造成浪费的方法。
问题一)在此,我们设计了四个方案。方案一,我们对2*2的正方形做了一个外切圆,圆心为服务站,如图1,当n=100时,我们需建立1156个服务站,此方案的优点是不会出现多个服务站都为同一个节点服务的现象,但因为圆的半径较小,所以需设的服务站较多。第二个方案中,以半径为2的圆相接,如图2,当 n=100时,需设645个服务站。此方案需建设较少的服务站,但却出现了多个服务站都为有一节点服务的现象。而第三个方案中,虽然同时用了半径为2的圆,但设置方法与方案二有所不同,如图4,n=100时,需设893个服务站,此方案服务了最大面积的范围,但其缺点也是需设置较多的服务站。在方案四中,当 时,需设置629个服务站,为最少。我们是从设置最少站点为优先考虑,因此,方案四为最优设计。
问题二)就第二个问题,我们需要知道城市的面积,有城市面积来设计我们的方案,而油费,服务站的建设成本以及其他花费来我们假设每个站的成本都相同。所以,我们所设置的每个快餐派送点能够服务最多的点且不造成过多的浪费,此方案就为最优方案。
问题重述
服务网点、通讯基站的设置,都存在如何设置较少的站点,获得较大的利益的问题。通讯基站的覆盖范围一般是圆形的,而消防、快餐、快递服务则受到道路情况和到达时间的限制。
现在我们将问题简化。假设城市道路构成一个 的正方形网格,交叉点称为节点,相邻节点的距离为1,。服务站设置在某个节点上,只能沿着道路对节点服务,并且最大服务距离为2。现在我们需要每个、节点都能得到服务,而服务站点最少,减少浪费,并对 时的最少服务站点数。又假设服务站是快餐派送网点,不考虑货源成本,需要哪些数据来确定服务站点的设置方案,并给出利润最大化得设置方法。
对于以上所述的问题,我们将通过建立数学模型的方法,以最少的服务站覆盖最多的节点,获取最大的经济利益。
模型的假设:
1. 假设城市道路构成一个 的正方形网格,用圆将正方形网络覆盖.尽量用最少的圆覆盖正方形网络的每一个节点。
2. 每个圆的圆心必须是网络的节点,取圆心为所设的服务网点。
3. 假设快餐派送网点与快餐需求量和供应量有关。
论文缩略图:

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
clc;clear;close all;
L=5;
R=2;
M=zeros(L);
N=0;
ss=1;
[m,n]=meshgrid(1:L)
axis([0,L,0,L]);
axis square;
hold on;
Ar=linspace(0,pi*2,200);
scale=0;
A1=gca;x=2; y=0; C=rand(1,3); axes(A1);grid onplot(x,y,'*','color',C); plot(x+i*y+R*exp(i*Ar),'color',C); x=5; y=2; C=rand(1,3); axes(A1);grid onplot(x,y,'*','color',C); plot(x+i*y+R*exp(i*Ar),'color',C); x=0; y=3; C=rand(1,3); axes(A1);grid onplot(x,y,'*','color',C); plot(x+i*y+R*exp(i*Ar),'color',C); x=3; y=5; C=rand(1,3); axes(A1);grid onplot(x,y,'*','color',C); plot(x+i*y+R*exp(i*Ar),'color',C);
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2010年认证杯SPSSPRO杯数学建模D题(第一阶段)服务网点的分布全过程文档及程序
2010年认证杯SPSSPRO杯数学建模 D题 服务网点的分布 原题再现: 服务网点、通讯基站的设置,都存在如何设置较少的站点,获得较大效益的问题。通讯基站的覆盖范围一般是圆形的,而消防、快餐、快递服务则受到道路情况和到达时间的限…...
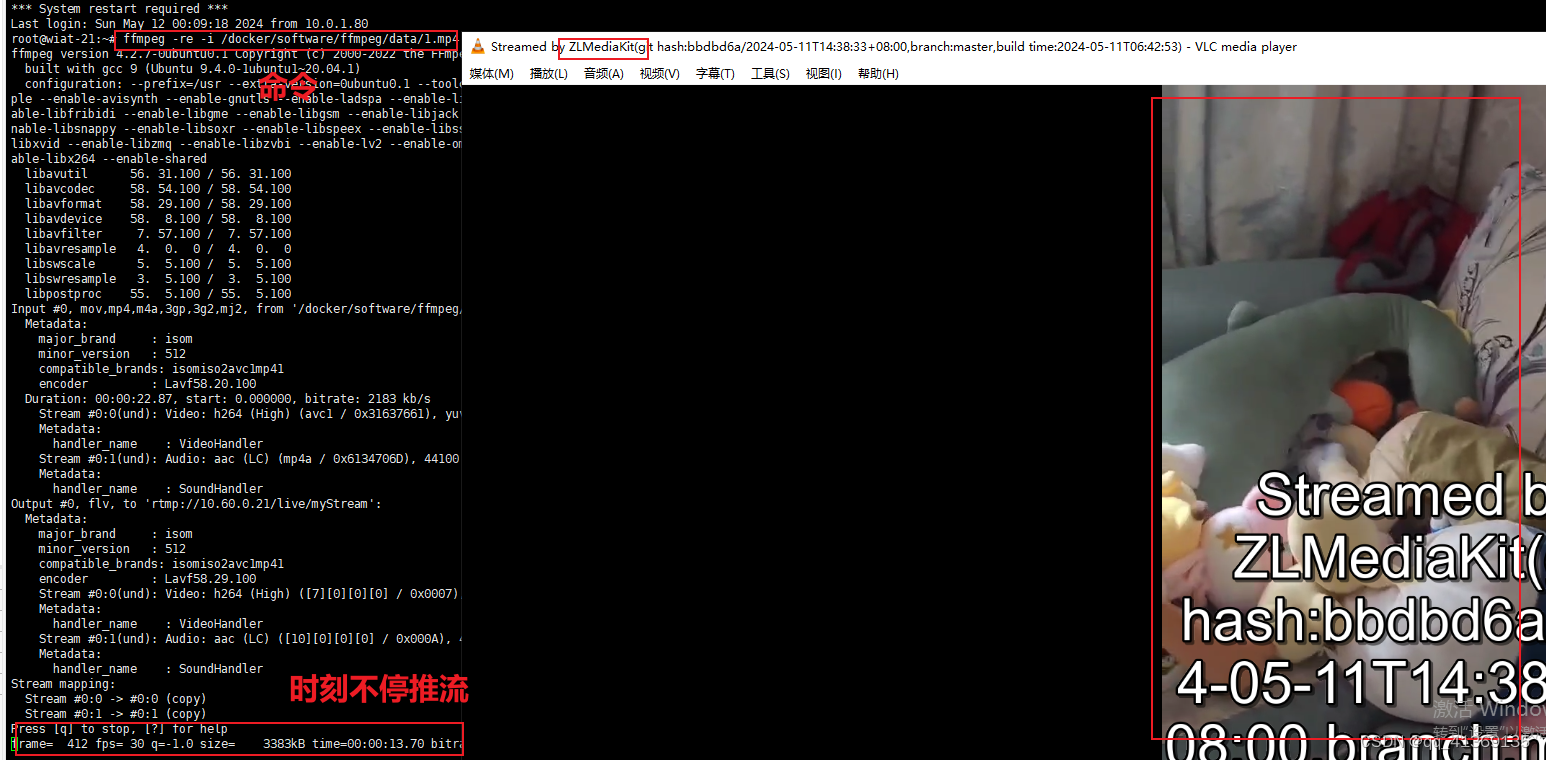
docker-compose 安装ZLMediaKit,ffmpeg、VLC实现推流并播放
1、目录(创建conf文件夹,777权限) 二、docker-compose.yml version: "3.9"services:zlmediakit:image: zlmediakit/zlmediakit:mastercontainer_name: zlmediakitprivileged: true# 指定加载配置# command: /opt/media/bin/MediaS…...

|Python新手小白中级教程|第二十八章:面向对象编程(类定义语法私有属性类的继承与多态)(4)
文章目录 前言一、类定义语法二、私有方法和私有属性1.私有属性2.私有方法 三、类“继承”1.初识继承2.使用super函数调用父类中构造的东西 四、类“多态”1.多态基础2.子类不同形态3.使用isinstance函数与多态结合判断类型 总结 前言 大家好,我是BoBo仔吖…...

vue项目基于WebRTC实现一对一音视频通话
效果 前端代码 <template><div class"flex items-center flex-col text-center p-12 h-screen"><div class"relative h-full mb-4 fBox"><video id"localVideo"></video><video id"remoteVideo">…...
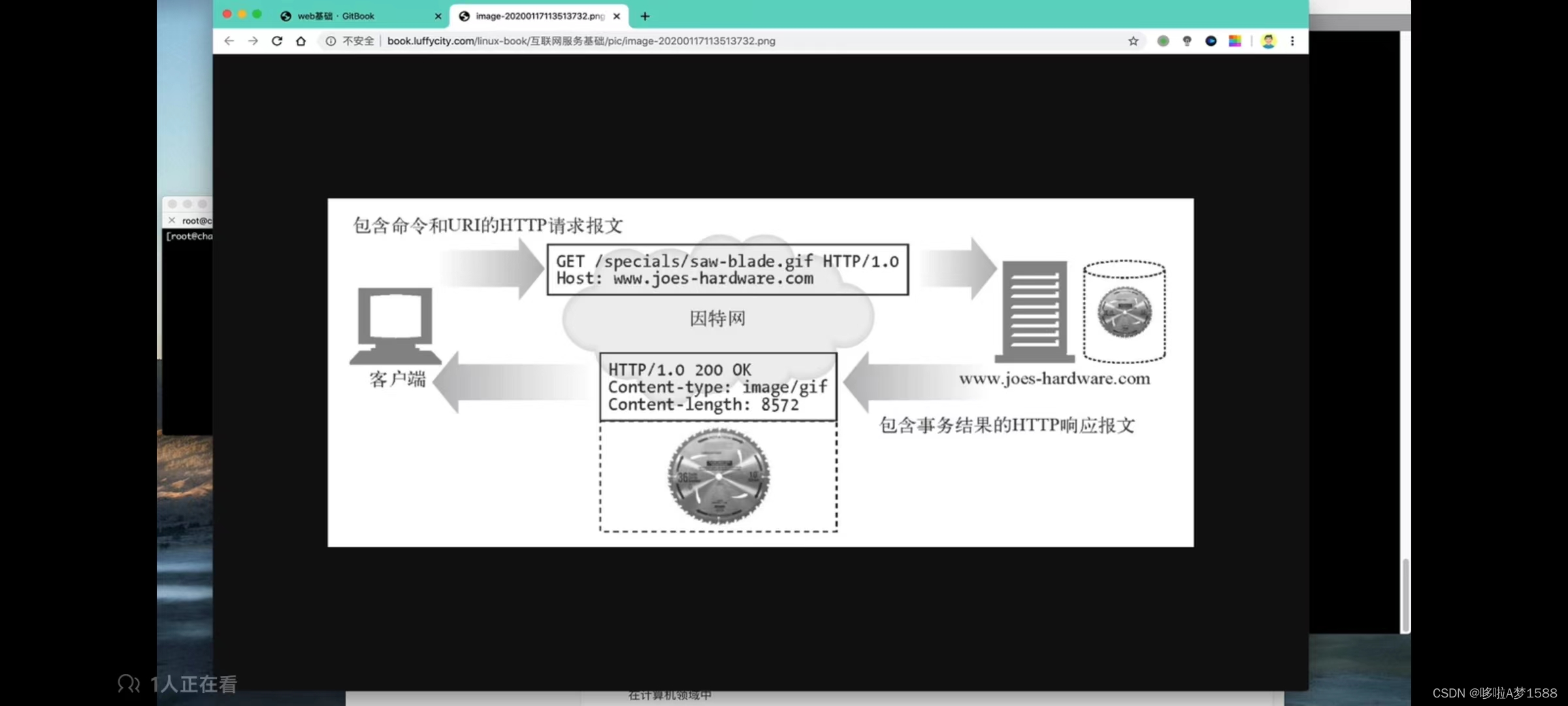
web 基础之 HTTP 请求
web 基础 网上冲浪 就是在互联网(internet)上获取各种信息,进行工作,或者娱乐,他的英文表示surfing the Internet,因 “surfing”d的意思是冲浪,即成为网上冲浪,这是一种形象说法, 也是一个非…...

嵌入式 - GPIO编程简介
An Introduction to GPIO Programming By Jeff Tranter Wednesday, June 12, 2019 编者按:本 2019 年博客系列是 ICS 最受欢迎的系列之一,现已更新(2022 年 12 月),以确保内容仍然准确、相关和有用。 本博客是 Integr…...
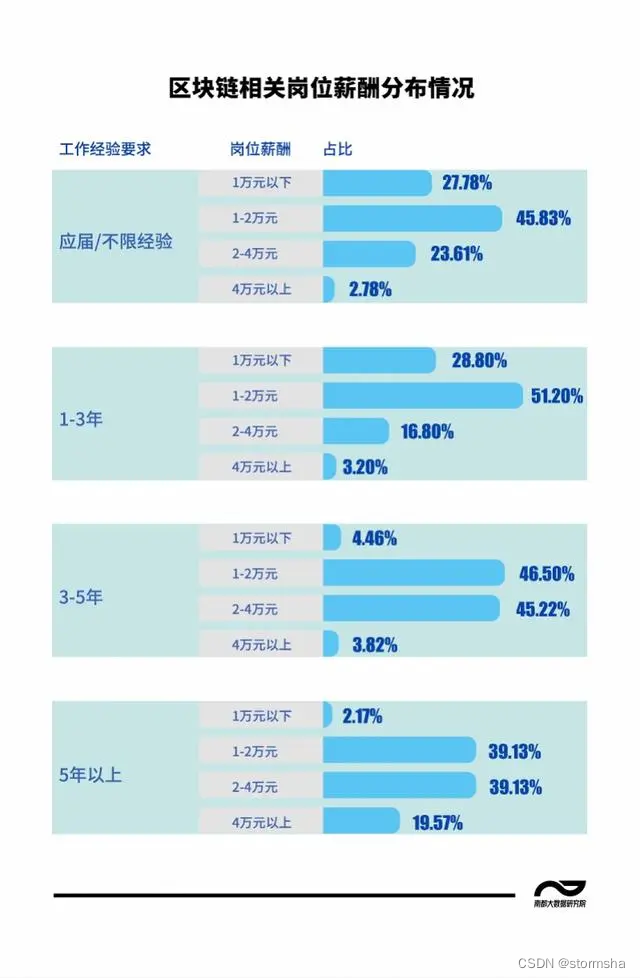
8种区块链开发者必须知道的顶级编程语言!
我来问你一个问题:请说出一种技术,它以去中心化、不可篡改和透明性等核心特征席卷了全球。 这个问题的答案是,当然是区块链,它在近些年进入大家的视野并颠覆了工商业,没有任何其他技术能够做到这一点。 预计从2020年…...
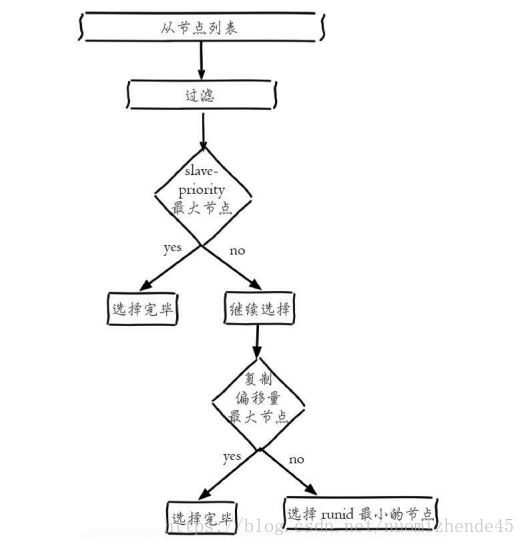
十三、Redis哨兵模式--Sentinel
上一篇介绍了Redis中的主从复制。我们知道Redis主从中一般只有主节点对外提供写操作,如果主节点发生故障,为了保证Redis的可用性,这时就要在可用的slave节点中,挑选一个作为主节点。这种切换操作如果是人为的操作,那么…...

[力扣题解]1005. K 次取反后最大化的数组和
题目:1005. K 次取反后最大化的数组和 思路 贪心法; 用绝对值大小排序,自己写一个比较函数, static bool compare(int a, int b) {return abs(a) > abs(b); }注意这样写出来是降序排列; 代码 class Solution {…...
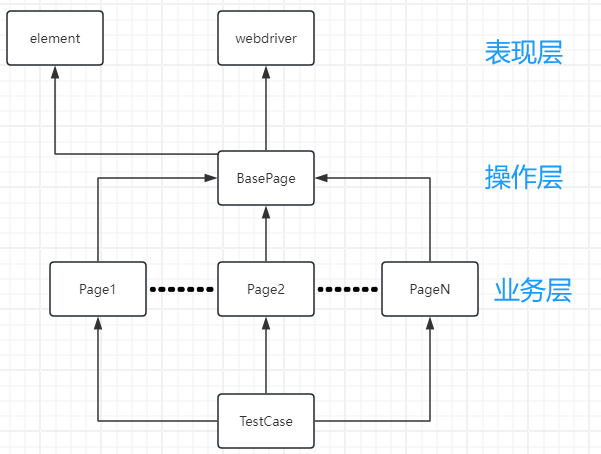
Web UI自动化测试--PO模式
没有PO实现的测试用例的问题: 重用性低:登录功能重复可维护性差:数据和代码混合可读性差:元素定位方法杂乱(id、xpath、css混杂)可读性差:不易识别操作的含义(特别是css和xpath语法)可维护性差:如果某个元素的属性改了,你要更改多次PO(Page Object Model)页面对象模型…...

Python进阶之-反射机制详解
✨前言: 什么是反射? Python中的“反射”是一个编程术语,它指的是程序在运行时能够检查和操作其自身状态的能力,特别是通过名称(通常是字符串)来访问对象的属性、方法和其他组成部分。这种机制允许代码动态…...

day05-面向对象内存原理和数组
day05 面向对象内存原理和数组 我们在之前已经学习过创建对象了,那么在底层中他是如何运行的。 1.对象内存图 1.1 Java 内存分配 Java 程序在运行时,需要在内存中分配空间。为了提高运算效率,就对空间进行了不同区域的划分,因为每一片区域…...
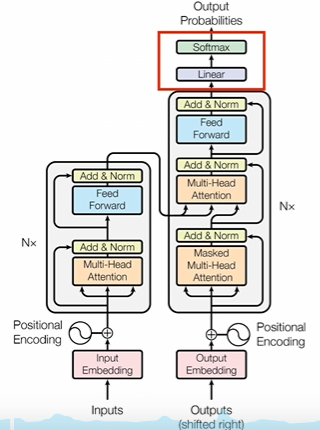
从头理解transformer,注意力机制(下)
交叉注意力 交叉注意力里面q和KV生成的数据不一样 自注意力机制就是闷头自学 解码器里面的每一层都会拿着编码器结果进行参考,然后比较相互之间的差异。每做一次注意力计算都需要校准一次 编码器和解码器是可以并行进行训练的 训练过程 好久不见输入到编码器&…...

ORA-609频繁出现在alert.log,如何解决?
ORA-609就alertlog中比较常见的一个报错,虽然并没有太大的影响,但是频繁的出现在alert log也是很让人厌烦的事情,本文介绍如何排查解决ORA-609问题。 1.ORA-609官方定义 could not attach to incoming connection Cause Oracle process cou…...
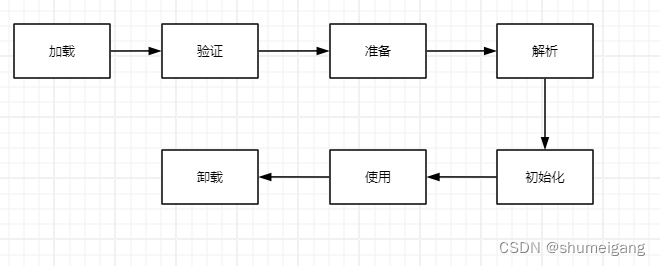
JVM 类加载机制
JVM 类加载机制分为五个部分:加载,验证,准备,解析,初始化,下面我们就分别来看一下这五个过程。 加载 加载是类加载过程中的一个阶段,这个阶段会在内存中生成一个代表这个类的 java.lang.class 对…...
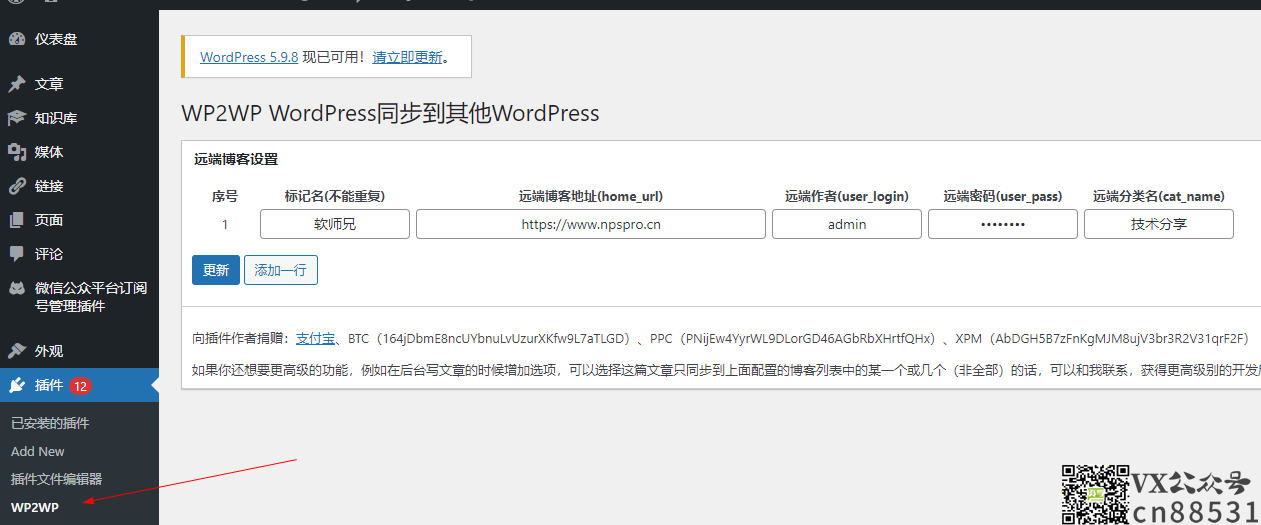
亲测-wordpress文章实时同步发布修改删除多个站点的WP2WP插件
一款将wordpress文章同步到其他WordPress网站的插件,通过这款插件,可以保持不同博客之间文章发布、修改、删除的同步。 安装步骤: 主站和分站都要上传这个插件 1.把插件上传到wp-content\plugins解压出来wp2wp文件夹,然后启用插…...

npm无法安装node-sass 的问题
安装 node-sass 的问题呈现:4.9.0版本无法下载 Downloading binary from https://github.com/sass/node-sass/releases/download/v4.9.0/win32-x64-72_binding.node Cannot download "https://github.com/sass/node-sass/releases/download/v4.9.0/win32-x64-…...
springboot 引入第三方bean
如何进行第三方bean的定义 参数进行自动装配...

安装Nginx
如果没有gcc环境,需要安装gcc yum install gcc-c安装依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel工作目录 mkdir /opt/nginx && cd /opt/nginx下载安装包 wget http://nginx.org/download/nginx-1.32.1.tar.gz解压安装包…...

爬虫工具you-get
you-get是一个简单易上手的爬虫小工具,可以从网络中爬取多媒体信息,包括图片、音频和视频。you-get的github项目地址为:https://github.com/soimort/you-get 一、安装 以下为相关依赖,需要分别安装: Python 3 (必须…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...
