第四届上海理工大学程序设计全国挑战赛 J.上学 题解 DFS 容斥
上学
题目描述
usst 小学里有 n 名学生,他们分别居住在 n 个地点,第 i 名学生居住在第 i 个地点,这些地点由 n−1 条双向道路连接,保证任意两个地点之间可以通过若干条双向道路抵达。学校则位于另外的第 0 个地点,第 0 个地点与第 1 个地点之间有另外一条双向道路链接。
最近学校开始启用校车来接学生上学,每一辆校车上都可以坐无限个学生,且每辆校车在一天内不会重复经过一条道路,校车终点始终为学校。每一位学生一天内只能乘坐一辆校车,且只能在自己居住的节点处上车,在学校下车。为了节省资金,学校会在保证每位学生都能坐上校车的前提下,安排最少数量的校车,每天早上从某些地点出发,并经过若干道路和地点最终抵达学校。第 x 位学生可以自由选择一辆经过第 x 个地点的校车,搭乘它到达学校。
现在学校想要从 n 个学生中选出 3 人参加某个比赛,但是学校不希望这 3 人之间太过 “熟悉”,请问一共有多少种不同的选人方案。
如果一种选择方案中, 3 个人可能在同一天里乘坐上同一辆校车,那就称这 3 个人之间太过 “熟悉”。
对于任意两个方案,如果存在一名学生在一个方案中且不在另一个方案中,那么就认为这两种方案不同。
输入描述
输入第 1 行包含 1 个正整数 n ,代表学生数量和学生居住的地点数量。( 3 ≤ n ≤ 2 × 1 0 5 3≤n≤2×10^5 3≤n≤2×105)
接下来 n−1 行每行有 2 个正整数 u, v ,代表第 u 个地点与第 v 个地点之间有一条双向道路。( 1 ≤ u , v ≤ n 1≤u,v≤n 1≤u,v≤n)
输出描述
输出一行,一个整数,代表选人方案数量。
样例输入 #1
5
1 2
2 3
3 4
4 5
样例输出 #1
0
样例输入 #2
5
1 2
2 3
2 4
1 5
样例输出 #2
8
原题
牛客——传送门
思路
根据题目描述可知,学校所选择的校车的路线是每个由叶子节点指向根节点(即节点1)的路径。题目目的是求出从 n 个学生中选择 3 个学生,保证 3 个学生不在同一条由叶子节点指向根节点(即节点1)的路径中的方案数。那么可以采用容斥原理,用不考虑 3 个学生在一条路径上的总的方案数减去 3 个学生在一条路径上的方案数。
求解示例如下:
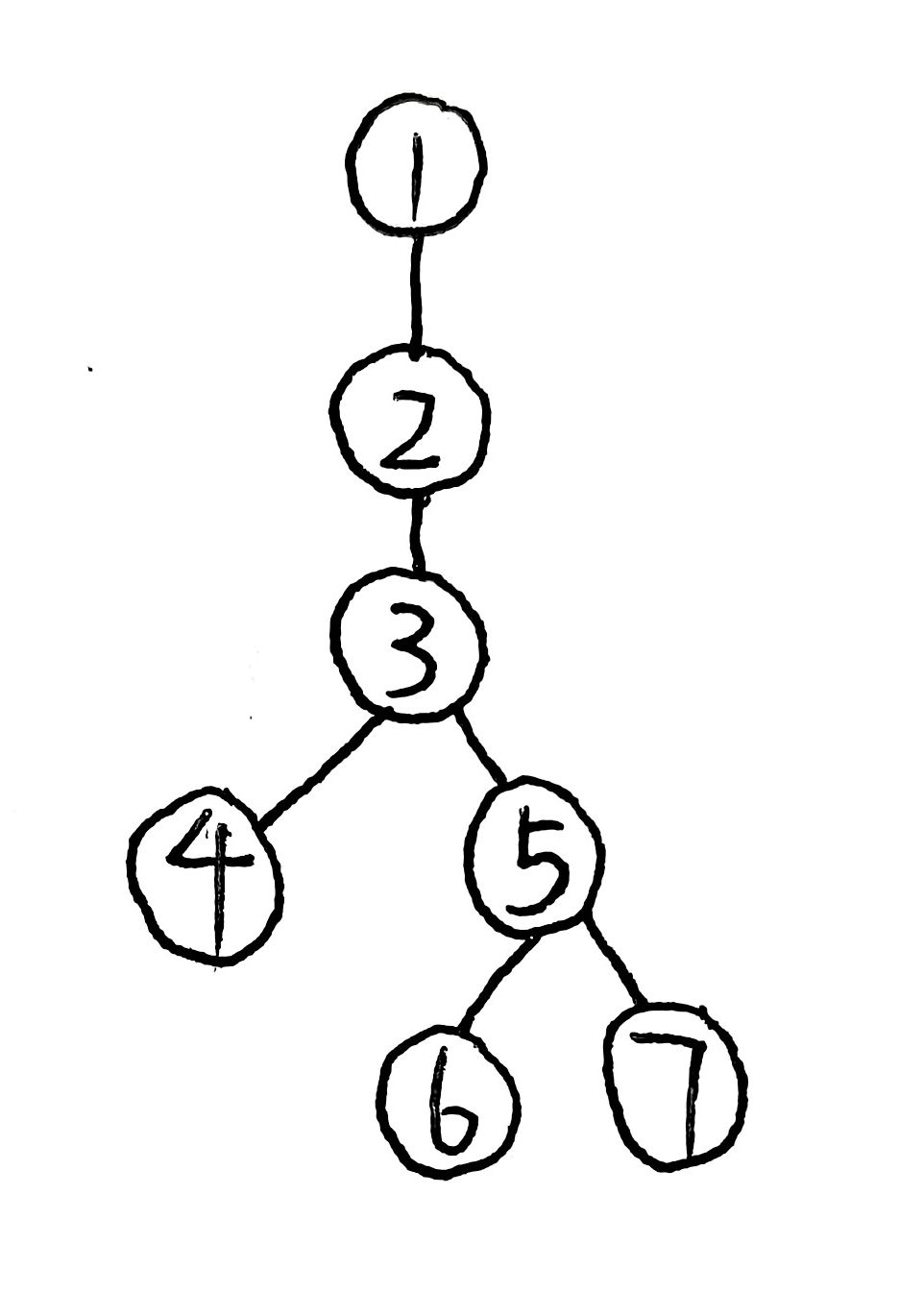
对于上图所示的树,存在三条从叶子节点到根节点的路径,即 4-1,6-1,7-1,也就是三辆校车行驶的路线。首先,总的方案数为C(n,3)。而 3 个学生在一条路径上的方案数求解如下:C(4,3)+C(5,3)+C(5,3)-C(4,3)-C(3,3)。意思是4-1,6-1,7-1的三条路径中各自分别选取 3 个学生,但是存在重复选取5-1路径和3-1路径的情况。所以我们需要去重,即因为 5 节点下面有两条支链,所以要减去5-1路径的方案数乘以2-1(因为有两条支链,重复求了一次,所以2-1表示多求的数量)即减去C(4,3)。同理,还需要减去3-1路径的方案数即C(3,3)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int maxn = 2e5 + 6;
vector<int> e[maxn]; // 邻接表存边
vector<pair<int, int>> num; // num.first为路径上的节点个数,num.second为该路径需要计算多少次void dfs(int p, int fa, int depth)
{if (p != 1 && e[p].size() <= 1) // 找到叶子节点{if (depth >= 3){num.push_back({depth, 1});}return;}int child_num = 0; // 支链数量,即孩子数量for (int i = 0; i < e[p].size(); i++) // 树的递归遍历{int v = e[p][i];if (v != fa){dfs(v, p, depth + 1);child_num++;}}if (depth >= 3) // 去重{num.push_back({-depth, child_num - 1}); // 加入num数组数指定为-depth,为的是做个标记}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);ll n;cin >> n;for (int i = 1; i < n; i++){int u, v;cin >> u >> v;// 存无向边e[u].push_back(v);e[v].push_back(u);}dfs(1, 0, 1);// 先计算总方案数C(n,3)ll ans = n * (n - 1) * (n - 2) / 6;for (int i = 0; i < num.size(); i++){ll x = num[i].first;if (x > 0) // 若为正数,表示这是叶子节点到根节点的路径中选取学生的方案数ans -= x * (x - 1) * (x - 2) / 6;else // 标记为负数,表示这是要去重的路径中选取学生的方案数{x = -x;ans += x * (x - 1) * (x - 2) / 6 * (ll)num[i].second;}}cout << ans;return 0;
}
相关文章:

第四届上海理工大学程序设计全国挑战赛 J.上学 题解 DFS 容斥
上学 题目描述 usst 小学里有 n 名学生,他们分别居住在 n 个地点,第 i 名学生居住在第 i 个地点,这些地点由 n−1 条双向道路连接,保证任意两个地点之间可以通过若干条双向道路抵达。学校则位于另外的第 0 个地点,第…...

word-排版文本基本格式
1、文本的基本格式:字体格式、段落格式 2、段落:word排版的基本控制单位 3、每敲一次回车,为一个段落标记,注意区分换行符和段落标记,换行符为指向下的箭头,段落标记为带拐弯的箭头,换行符&…...
)
目标检测YOLO实战应用案例100讲-无监督领域自适应目标检测方法研究与应用(五)
目录 多源无监督领域自适应目标检测方法 4.1研究现状及问题形成 4.2相关工作详述...
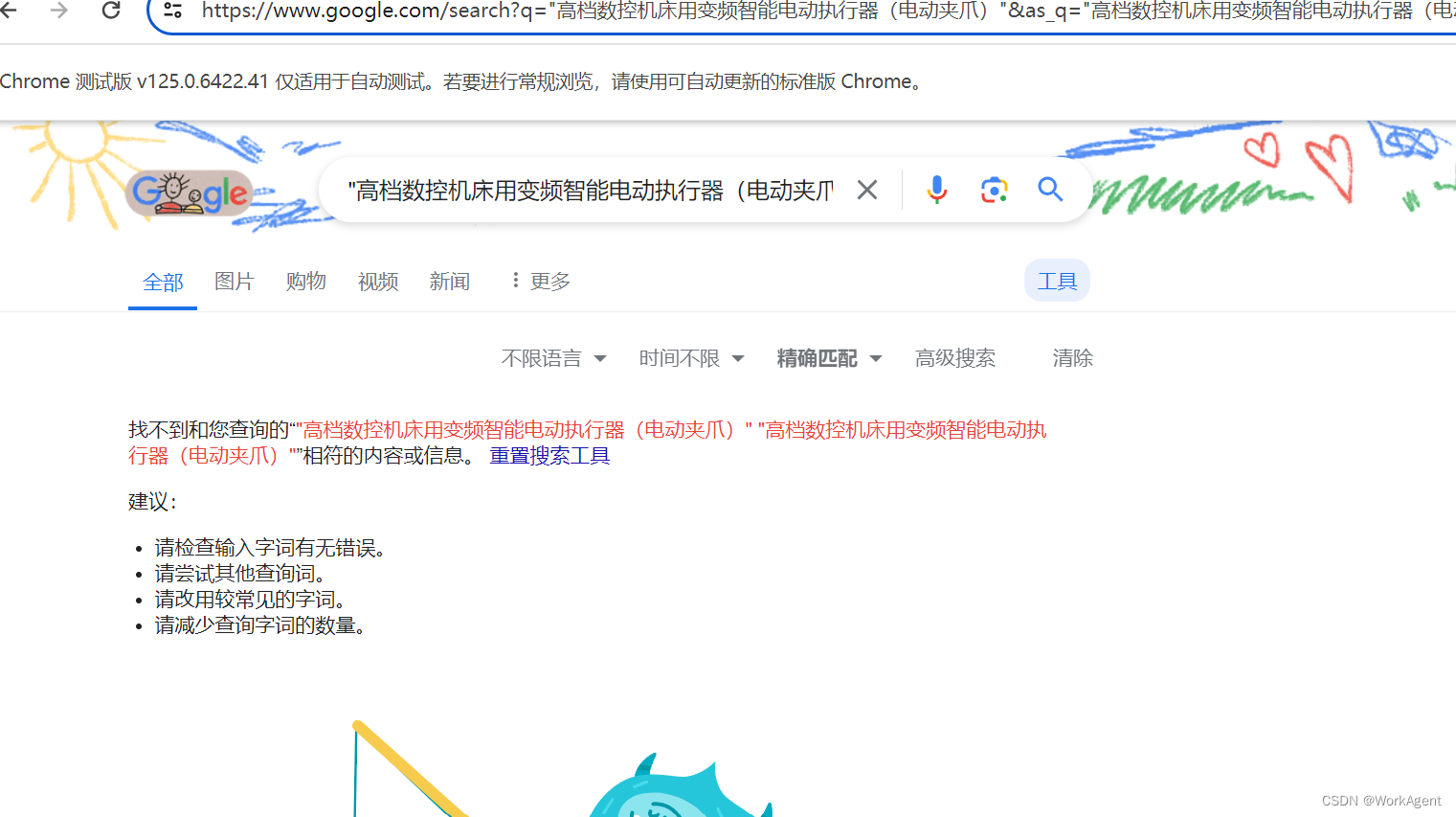
通过python实现Google的精准搜索
问题背景: 我想通过Google或者其他网站通过精准搜索确认该产品是否存在,但是即使该产品不存在Google也会返回一些相关的url链接,现在想通过python实现搜索结果的精准匹配以确认该产品是否为正确的名称【可以通过google搜索到,如果…...
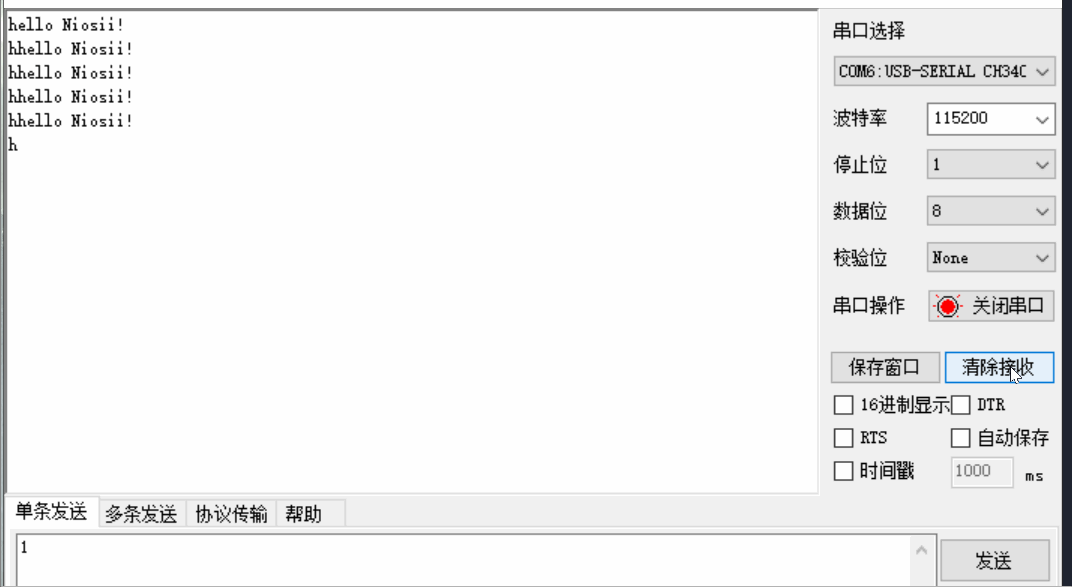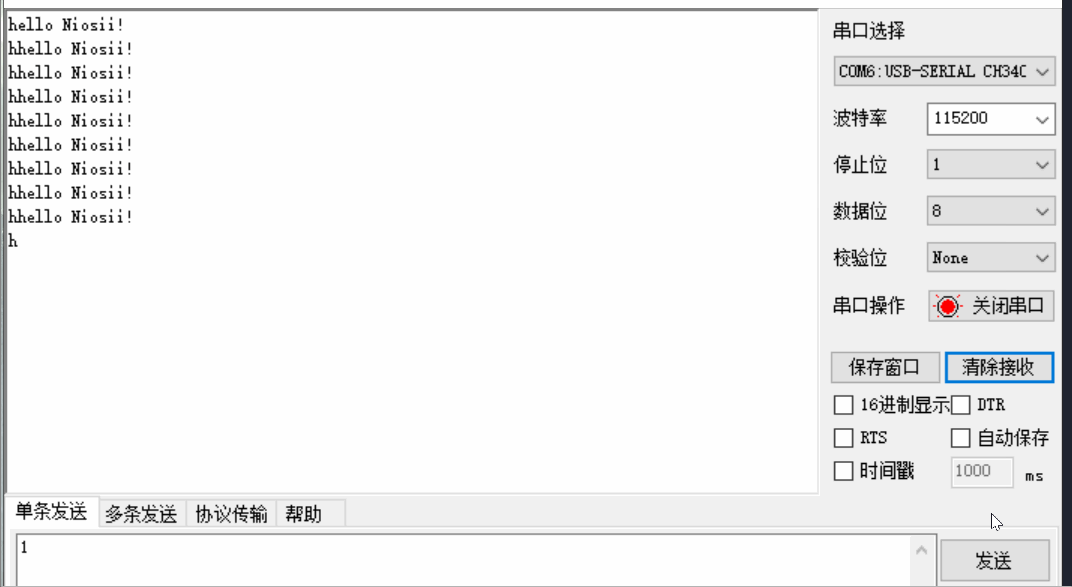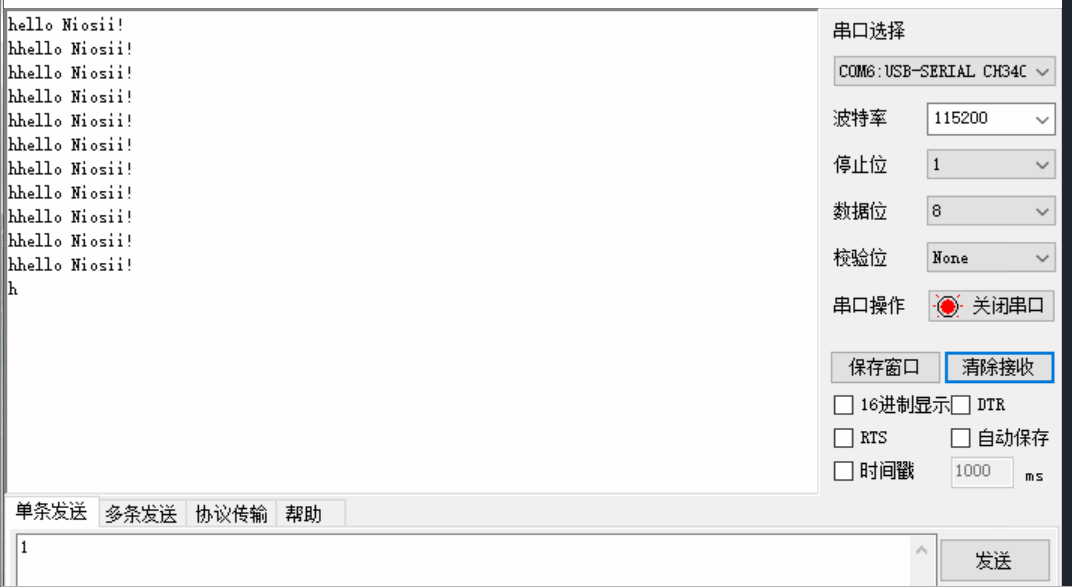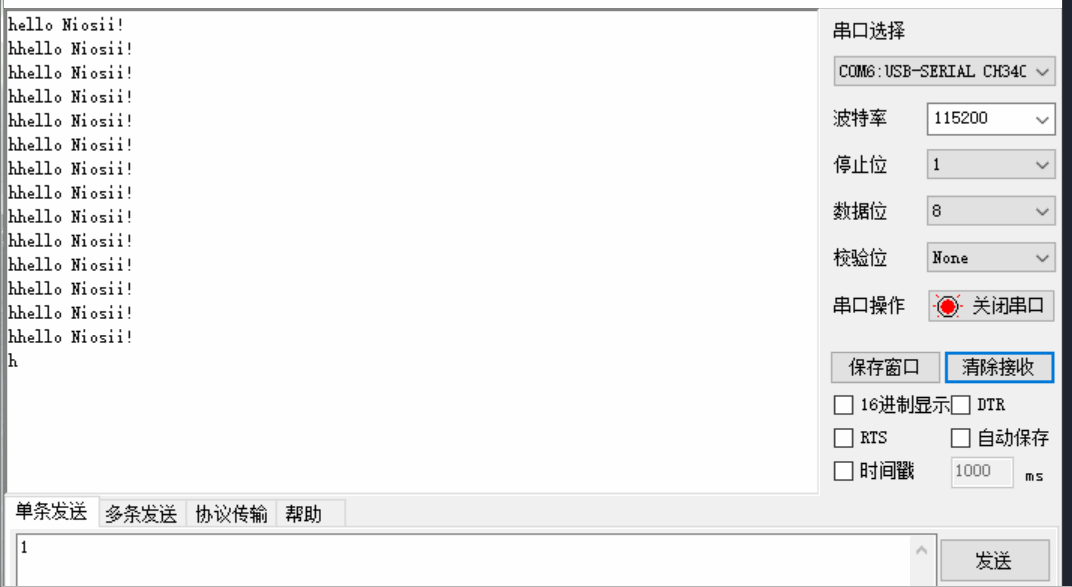
Nios-II编程入门实验
文章目录 一 Verilog实现流水灯二 Nios实现流水灯2.1 创建项目2.2 SOPC添加模块2.3 SOPC输入输出连接2.4 Generate2.5 软件部分2.6 运行结果 三 Verilog实现串口3.1 代码3.2 引脚3.3 效果 四 Nios2实现串口4.1 sopc硬件设计4.2 top文件4.3 软件代码4.4 实现效果 五 参考资料六 …...

从0开始学python(七)
目录 前言 1 break、continue和pass函数 1.1 break 1.2 continue 1.3 pass 2、序列的索引及切片操作 2.1字符串的索引和切片 2.1.1 字符串索引 2.1.2 字符串切片 总结 前言 上一篇文章我们介绍了python中的循环结构,包括for和while的使用。本章接着往下讲。…...

【二叉树算法题记录】404. 左叶子之和
题目描述 给定二叉树的根节点 root ,返回所有左叶子之和。 题目分析 其实这题无论是迭代法还是递归法,最重要的是要明确判断左叶子的条件:当前节点有左孩子,且这个左孩子没有它的左孩子和右孩子。 迭代法 感觉只要二叉树相关…...
面试集中营—Spring篇
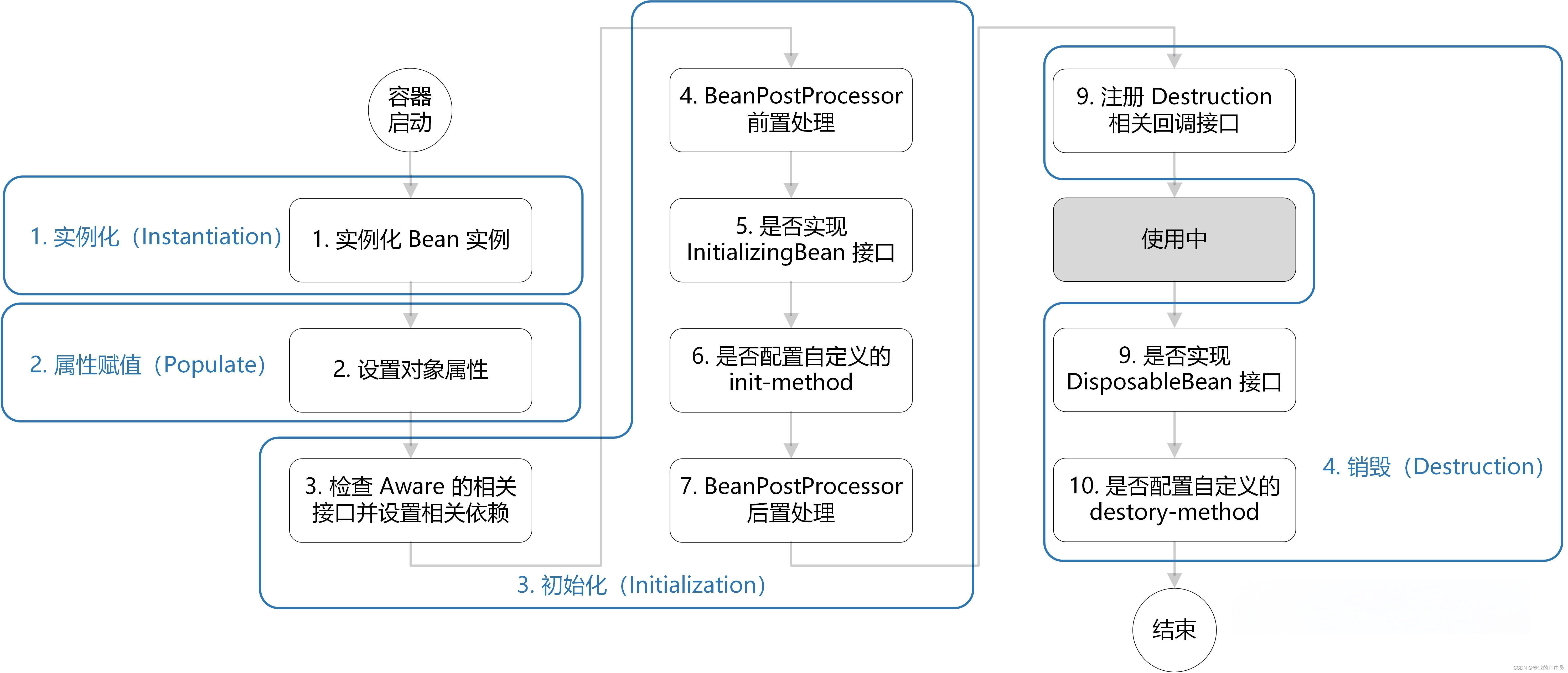
Spring 框架的好处 1、轻量:spring是轻量的,基本的版本大约2MB; 2、IOC:控制反转,Spring的IOC机制使得对象之间的依赖不再需要我们自己来控制了,而是由容易来控制,一个字:爽…...
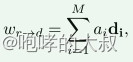
Lia 原理
训练阶段 论文流程: 具体实现: 通过latent space传递运动信息,实现分两部分。 1)image space->latent space 将源图像映射到隐空间编码。X_s (source image )映射到编码Z_sr,通过W_rd方向上的变化,得到新的编码Z…...

文本批量操作技巧:内容查找不再繁琐,自动化批量移动至指定文件夹
在文本处理和信息管理的日常工作中,我们经常需要处理大量的文件和数据。面对这些海量的信息,如何快速而准确地查找特定的内容,并将它们批量移动至指定的文件夹,成为了一项关键的技能。本文将介绍办公提效工具一些实用的文本批量操…...

[数据结构]动画详解单链表
💖💖💖欢迎来到我的博客,我是anmory💖💖💖 又和大家见面了 欢迎来到动画详解数据结构系列 用通俗易懂的动画的动画使数据结构可视化 先来自我推荐一波 个人网站欢迎访问以及捐款 推荐阅读 如何低…...
图片批量管理迈入智能新时代:一键输入关键词,自动生成并保存惊艳图片,轻松开启创意之旅!
在数字化时代,图片已成为我们表达创意、记录生活、传递信息的重要工具。然而,随着图片数量的不断增加,如何高效、便捷地管理这些图片,却成为了一个令人头疼的问题。 第一步,进入首助编辑高手主页面,在上方…...
【硬件模块】ESP-01SWiFi模块基于AT指令详解(WiFi,TCP/IP,MQTT)
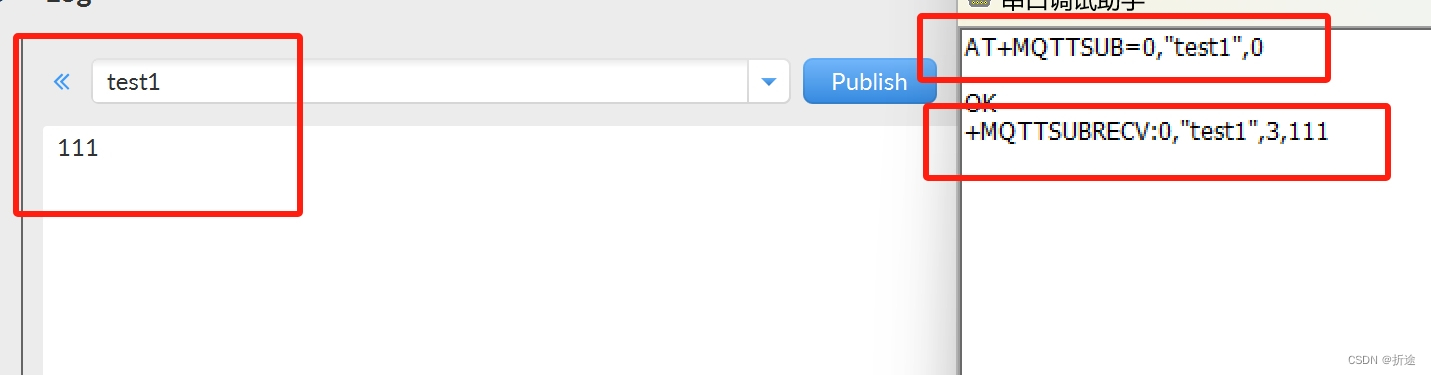
ESP-01S ESP-01S是由安信可科技开发的一款Wi-Fi模块。其核心处理器是ESP8266,该处理器在较小尺寸的封装中集成了业界领先的Tensilica L106超低功耗32位微型MCU,带有16位精简模式,主频支持80MHz和160MHz,并集成了Wi-Fi MAC/BB/RF/P…...
数据结构之单单单——链表
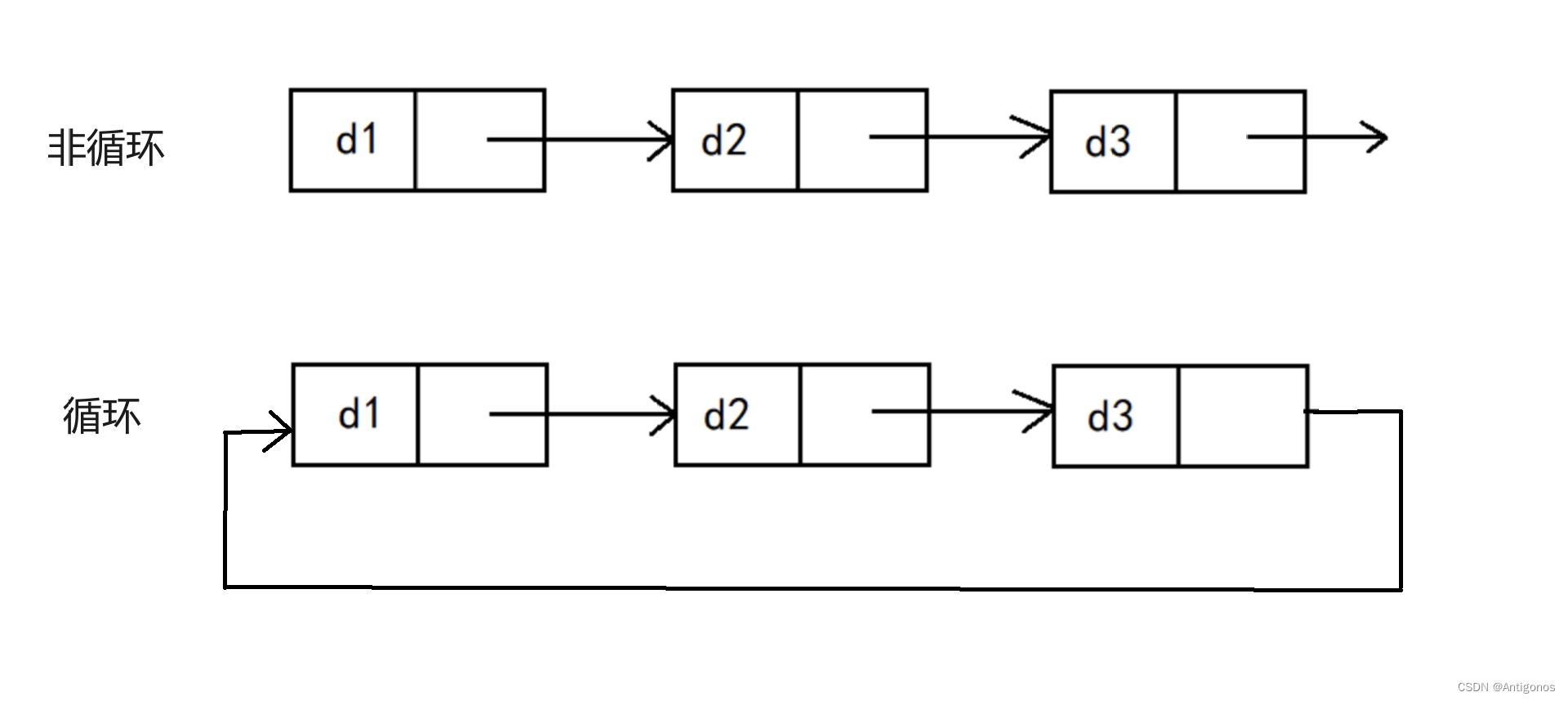
目录 一.链表 1)链表的概念 2)链表的结构 二.单链表的实现 三.链表的分类 1)单向或者双向 2)带头或不带头 3)循环或非循环 一.链表 1)链表的概念 链表(Linked List)是一种…...

【Linux笔记】 基础指令(二)
风住尘香花已尽 日晚倦梳头 重命名、剪切指令 -- mv 简介: mv 命令是 move 的缩写,可以用来移动文件或者将文件改名,是 Linux 系统下常用的命令,经常用来备份文件或者目录 语法: mv [选项] 源文件或目录 目标文件或目录…...
软件全套资料梳理(需求、开发、实施、运维、安全、测试、交付、认证、评审、投标等)
软件全套精华资料包清单部分文件列表: 工作安排任务书,可行性分析报告,立项申请审批表,产品需求规格说明书,需求调研计划,用户需求调查单,用户需求说明书,概要设计说明书,…...

javacv实时解析pcm音频流
javacv实时解析pcm音频流 解析代码 try (ByteArrayInputStream inputStream new ByteArrayInputStream(bytes);){FFmpegFrameGrabber grabber new FFmpegFrameGrabber(inputStream);// PCM S16LE 格式grabber.setFormat("s16le");// 采样率grabber.setSampleRate(1…...
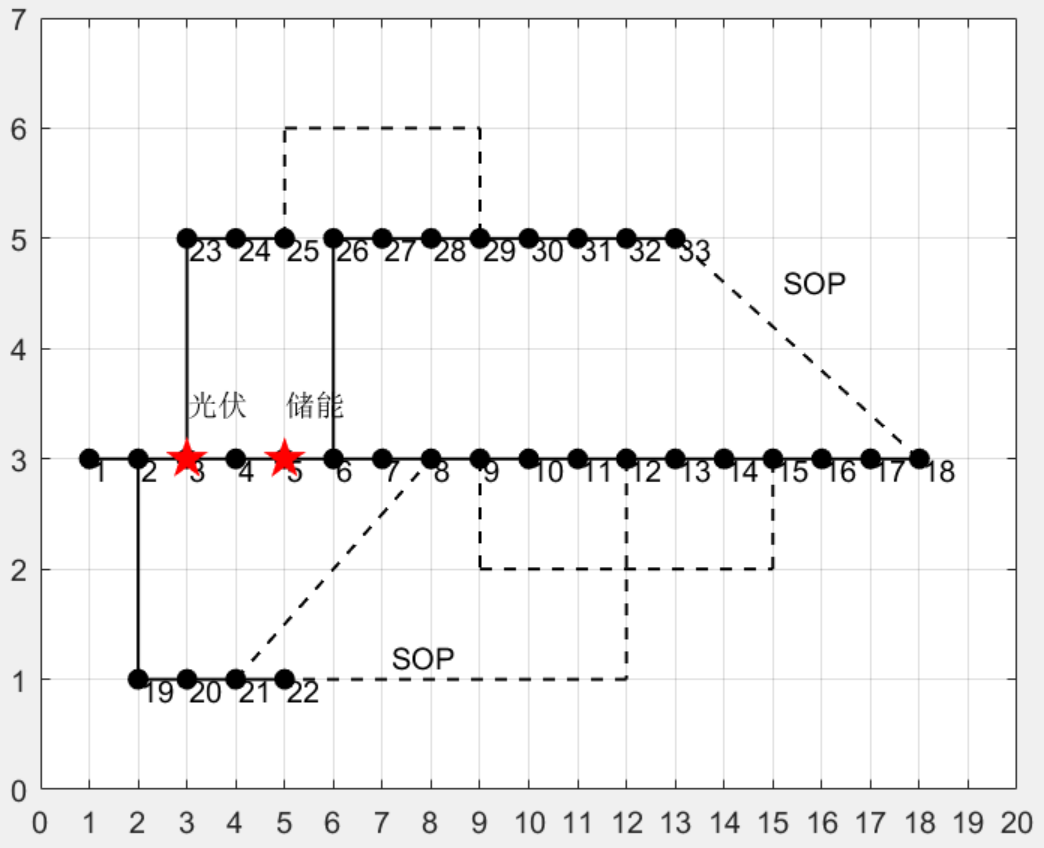
Matlab|考虑极端天气线路脆弱性的配电网分布式电源和储能优化配置模型
1主要内容 程序主要参考《考虑极端天气线路脆弱性的配电网分布式电源配置优化模型-马宇帆》,针对极端天气严重威胁配电网安全稳定运行的问题。基于微气象、微地形对配电网的线路脆弱性进行分析,然后进行分布式电源接入位置与极端天气的关联性分析&#…...

【Python基础】装饰器(3848字)
文章目录 [toc]闭包什么是装饰器装饰器示例不使用装饰器语法使用装饰器语法 装饰器传参带参数的装饰器类装饰器魔术方法\__call__()类装饰器示例带参数类装饰器property装饰器分页操作商品价格操作 个人主页:丷从心 系列专栏:Python基础 学习指南&…...
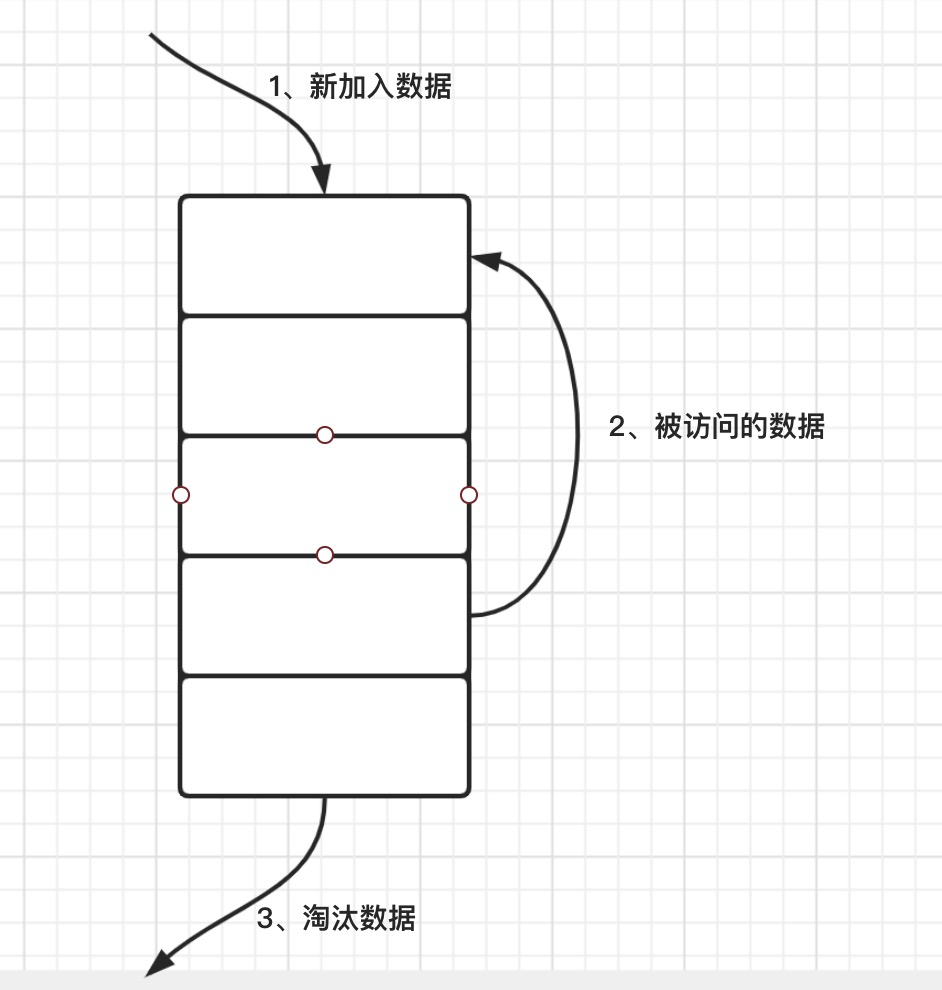
十、Redis内存回收策略和机制
1、Redis的内存回收 在Redis中可以设置key的过期时间,以期可以让Redis回收内存,循环使用。在Redis中有4个命令可以设置Key的过期时间。分别为 expire、pexpire、expireat、pexpireat。 1.1、expire expire key ttl:将key的过期时间设置为tt…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
