【二叉树算法题记录】404. 左叶子之和
题目描述
给定二叉树的根节点 root ,返回所有左叶子之和。
题目分析
其实这题无论是迭代法还是递归法,最重要的是要明确判断左叶子的条件:当前节点有左孩子,且这个左孩子没有它的左孩子和右孩子。
迭代法
感觉只要二叉树相关的题递归想不出来,直接暴力上层序遍历就能解出来。迭代法真没什么难度,就是把内层while循环中处理当前节点的条件换成上面的逻辑就行,也即:
if(node->left && node->left->left==NULL && node->left->right == NULL) sum += node->left->val;
整体cpp代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {// 迭代法(层序遍历)queue<TreeNode*> q;int sum = 0;if(root!=NULL) q.push(root);while(!q.empty()){int size = q.size();while(size--){TreeNode* node = q.front();q.pop();if(node->left && node->left->left==NULL && node->left->right == NULL) sum += node->left->val;if(node->left) q.push(node->left);if(node->right) q.push(node->right);}}return sum;}
};
递归法
这里我和代码随想录中处理的不太一样,但是思路是一样的。我这里用了传出参数vector<int>& sum,所以我用什么遍历顺序都是对的。但是代码随想录中是用了int返回值,所以是要从下层传结果送至上层汇聚,那么这就必须要用后序遍历(左右中)。
我的cpp整体递归代码
注意:这里中左右的顺序可以任意变换,已经试过了,都能AC。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur, vector<int>& sum){// 递归终止条件if(cur == NULL) return;if(cur->left) traversal(cur->left, sum);if(cur->right) traversal(cur->right, sum);// 单层递归逻辑:当该节点只有一个左孩子(左叶子)if(cur->left!=NULL && cur->left->left==NULL && cur->left->right==NULL){sum.push_back(cur->left->val);}}int sumOfLeftLeaves(TreeNode* root) {// 递归法vector<int> sum;traversal(root, sum);return accumulate(sum.begin(), sum.end(), 0);}
};
代码随想录的cpp整体递归代码
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left); // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right); // 右int sum = leftValue + rightValue; // 中return sum;}
};相关文章:

【二叉树算法题记录】404. 左叶子之和
题目描述 给定二叉树的根节点 root ,返回所有左叶子之和。 题目分析 其实这题无论是迭代法还是递归法,最重要的是要明确判断左叶子的条件:当前节点有左孩子,且这个左孩子没有它的左孩子和右孩子。 迭代法 感觉只要二叉树相关…...
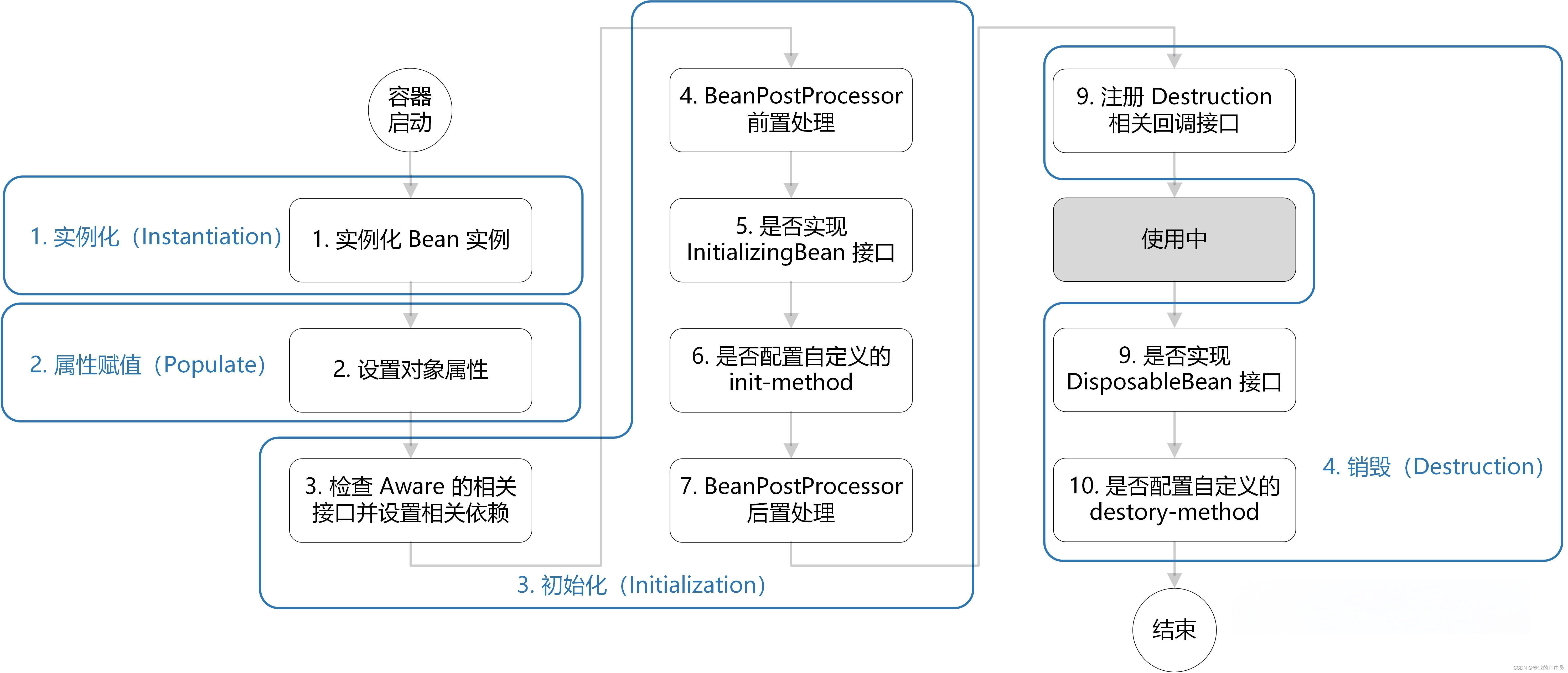
面试集中营—Spring篇
Spring 框架的好处 1、轻量:spring是轻量的,基本的版本大约2MB; 2、IOC:控制反转,Spring的IOC机制使得对象之间的依赖不再需要我们自己来控制了,而是由容易来控制,一个字:爽…...
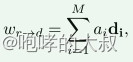
Lia 原理
训练阶段 论文流程: 具体实现: 通过latent space传递运动信息,实现分两部分。 1)image space->latent space 将源图像映射到隐空间编码。X_s (source image )映射到编码Z_sr,通过W_rd方向上的变化,得到新的编码Z…...

文本批量操作技巧:内容查找不再繁琐,自动化批量移动至指定文件夹
在文本处理和信息管理的日常工作中,我们经常需要处理大量的文件和数据。面对这些海量的信息,如何快速而准确地查找特定的内容,并将它们批量移动至指定的文件夹,成为了一项关键的技能。本文将介绍办公提效工具一些实用的文本批量操…...

[数据结构]动画详解单链表
💖💖💖欢迎来到我的博客,我是anmory💖💖💖 又和大家见面了 欢迎来到动画详解数据结构系列 用通俗易懂的动画的动画使数据结构可视化 先来自我推荐一波 个人网站欢迎访问以及捐款 推荐阅读 如何低…...
图片批量管理迈入智能新时代:一键输入关键词,自动生成并保存惊艳图片,轻松开启创意之旅!
在数字化时代,图片已成为我们表达创意、记录生活、传递信息的重要工具。然而,随着图片数量的不断增加,如何高效、便捷地管理这些图片,却成为了一个令人头疼的问题。 第一步,进入首助编辑高手主页面,在上方…...
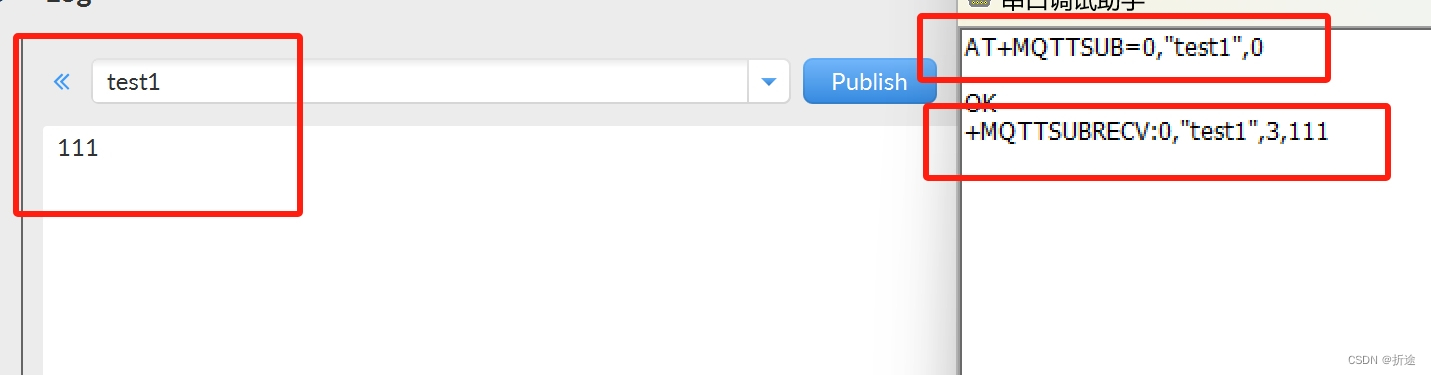
【硬件模块】ESP-01SWiFi模块基于AT指令详解(WiFi,TCP/IP,MQTT)
ESP-01S ESP-01S是由安信可科技开发的一款Wi-Fi模块。其核心处理器是ESP8266,该处理器在较小尺寸的封装中集成了业界领先的Tensilica L106超低功耗32位微型MCU,带有16位精简模式,主频支持80MHz和160MHz,并集成了Wi-Fi MAC/BB/RF/P…...
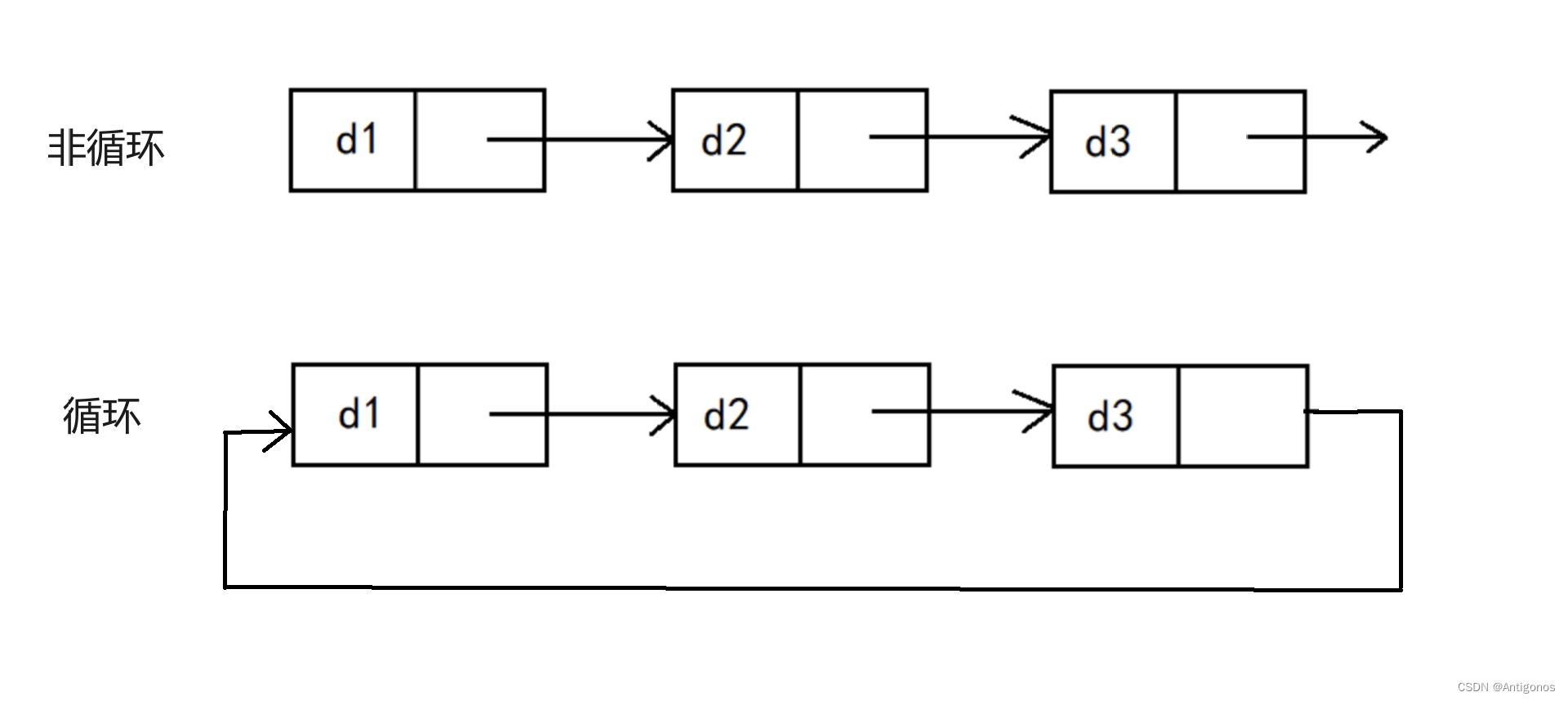
数据结构之单单单——链表
目录 一.链表 1)链表的概念 2)链表的结构 二.单链表的实现 三.链表的分类 1)单向或者双向 2)带头或不带头 3)循环或非循环 一.链表 1)链表的概念 链表(Linked List)是一种…...

【Linux笔记】 基础指令(二)
风住尘香花已尽 日晚倦梳头 重命名、剪切指令 -- mv 简介: mv 命令是 move 的缩写,可以用来移动文件或者将文件改名,是 Linux 系统下常用的命令,经常用来备份文件或者目录 语法: mv [选项] 源文件或目录 目标文件或目录…...
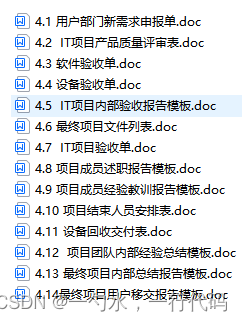
软件全套资料梳理(需求、开发、实施、运维、安全、测试、交付、认证、评审、投标等)
软件全套精华资料包清单部分文件列表: 工作安排任务书,可行性分析报告,立项申请审批表,产品需求规格说明书,需求调研计划,用户需求调查单,用户需求说明书,概要设计说明书,…...

javacv实时解析pcm音频流
javacv实时解析pcm音频流 解析代码 try (ByteArrayInputStream inputStream new ByteArrayInputStream(bytes);){FFmpegFrameGrabber grabber new FFmpegFrameGrabber(inputStream);// PCM S16LE 格式grabber.setFormat("s16le");// 采样率grabber.setSampleRate(1…...
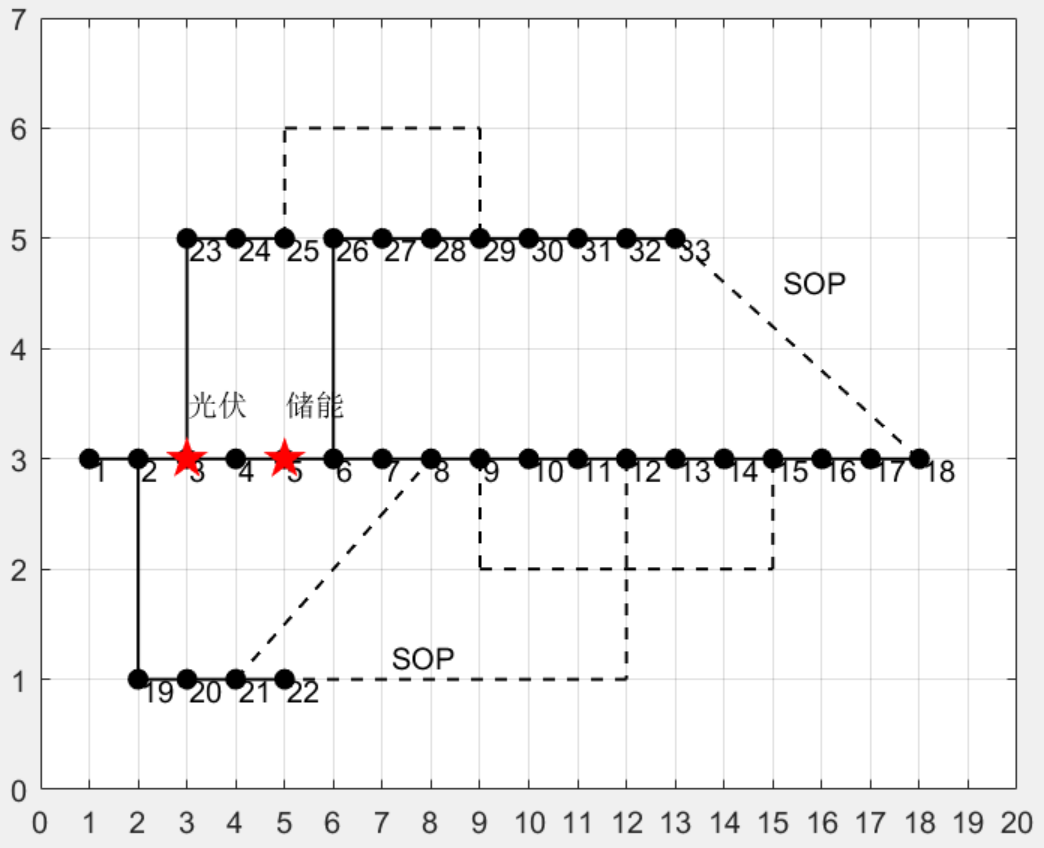
Matlab|考虑极端天气线路脆弱性的配电网分布式电源和储能优化配置模型
1主要内容 程序主要参考《考虑极端天气线路脆弱性的配电网分布式电源配置优化模型-马宇帆》,针对极端天气严重威胁配电网安全稳定运行的问题。基于微气象、微地形对配电网的线路脆弱性进行分析,然后进行分布式电源接入位置与极端天气的关联性分析&#…...

【Python基础】装饰器(3848字)
文章目录 [toc]闭包什么是装饰器装饰器示例不使用装饰器语法使用装饰器语法 装饰器传参带参数的装饰器类装饰器魔术方法\__call__()类装饰器示例带参数类装饰器property装饰器分页操作商品价格操作 个人主页:丷从心 系列专栏:Python基础 学习指南&…...
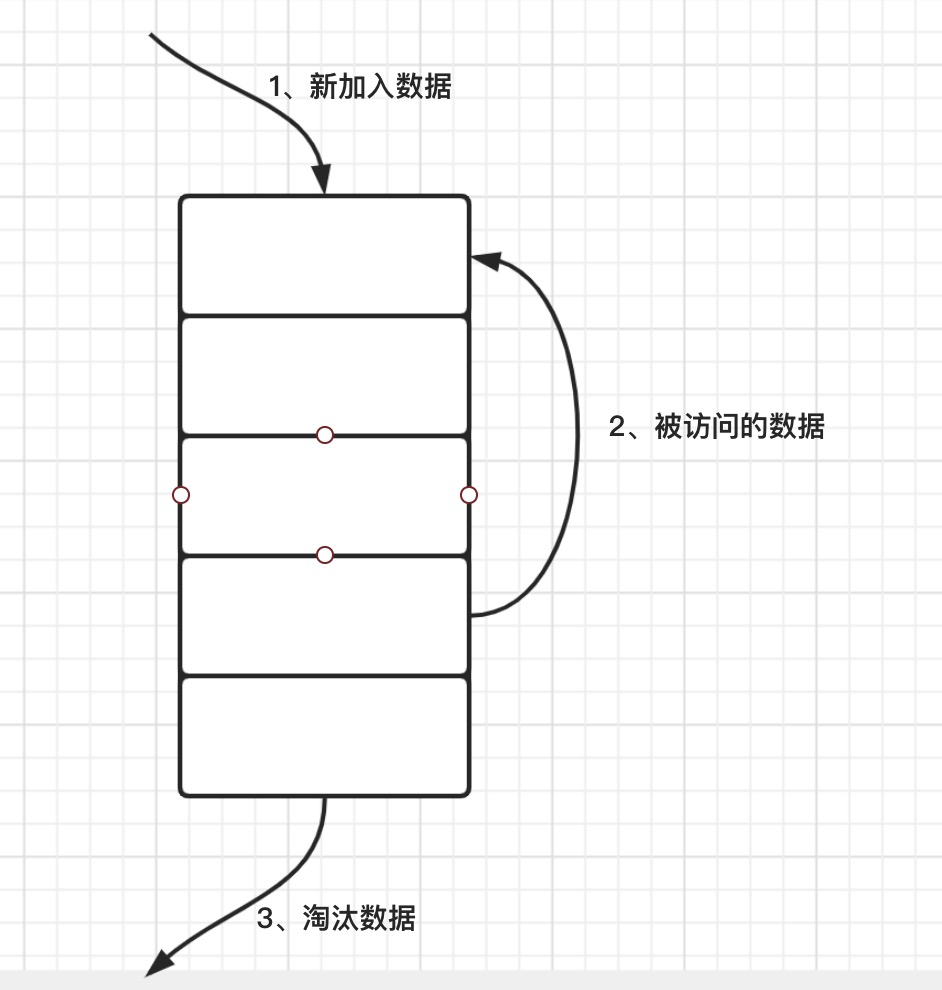
十、Redis内存回收策略和机制
1、Redis的内存回收 在Redis中可以设置key的过期时间,以期可以让Redis回收内存,循环使用。在Redis中有4个命令可以设置Key的过期时间。分别为 expire、pexpire、expireat、pexpireat。 1.1、expire expire key ttl:将key的过期时间设置为tt…...
Ansible --- playbook 脚本+inventory 主机清单
一 inventory 主机清单 Inventory支持对主机进行分组,每个组内可以定义多个主机,每个主机都可以定义在任何一个或 多个主机组内。 如果是名称类似的主机,可以使用列表的方式标识各个主机。vim /etc/ansible/hosts[webservers]192.168.10.1…...

【hive】transform脚本
文档地址:https://cwiki.apache.org/confluence/display/Hive/LanguageManualTransform 一、介绍二、实现1.脚本上传到本地2.脚本上传到hdfs 三、几个需要注意的点1.脚本名不要写全路径2.using后面语句中,带不带"python"的问题3.py脚本Shebang…...

5款可用于LLMs的爬虫工具/方案
5款可用于LLMs的爬虫工具/方案 Crawl4AI 功能: 提取语义标记的数据块为JSON格式,提供干净的HTML和Markdown文件。 用途: 适用于RAG(检索增强生成)、微调以及AI聊天机器人的开发。 特点: 高效数据提取,支持LLM格式,多U…...

投影、选择转SQL语言
使用以下两个表进行举例,第一个表为R表,第二个表为S表 R.AR.BR.C123456789 S.AS.BS.C101112131415161718 1、投影转SQL语言: 兀 A,B,C (R) 等价于select A,B,C from R 解释: 兀:相当于select (R):相当于from R…...

系统加固-自用
一、windows 1、概述 (1)、权限最高:system(系统账户),权限比administrator权限还高 (2)、常见操作系统安全漏洞类型 缓冲区溢出漏洞TCP/IP协议漏洞web应用安全漏洞开放端口的安全漏洞 2、系统安全加固方法 (1)、系统不显示上次登录的用户名 进入…...

Java面试题:阐述Java中的自动装箱与拆箱机制,以及使用它们时可能遇到的性能问题
在Java中,自动装箱(Autoboxing)和拆箱(Unboxing)是Java 5引入的特性,它们允许基本数据类型和对应的包装类之间的自动转换。 自动装箱 自动装箱是指将基本数据类型(如int、double等)…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
