数据与结构--堆
堆
堆的概念
堆:如果有一个关键码的集合K={k0,k1,k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足ki<=k2i+1且ki<=k2i+2(或满足ki>=k2i+1且ki>=k2i+2),其中i=0,1,2,…,则称该集合为堆。
-
堆序性质:在堆中,父节点的值要么大于等于(最大堆)或小于等于(最小堆)其子节点的值。这个性质是堆的核心特征。
-
完全二叉树结构:堆通常是一棵完全二叉树,即除了最底层外,其他层的节点都是满的,而且最底层的节点都集中在最左边。这意味着在堆中插入和删除节点时,树的形状会发生变化,但始终保持完全二叉树的性质。
-
最大堆和最小堆:堆分为最大堆和最小堆。
- 最大堆:每个父节点的值都大于等于其子节点的值。根节点是堆中的最大值。
- 最小堆:每个父节点的值都小于等于其子节点的值。根节点是堆中的最小值。
堆的结构
大根堆示例
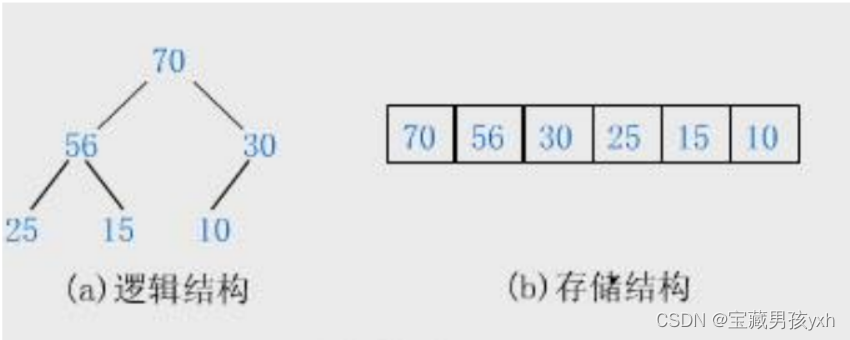
小根堆示例
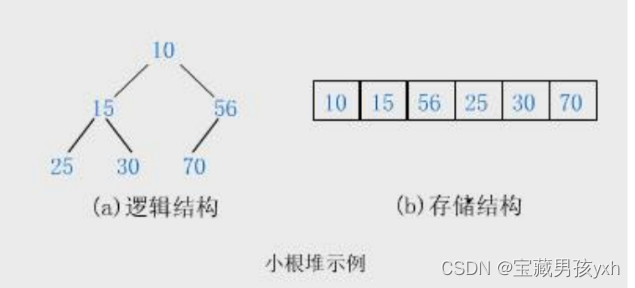
堆的向下调整算法
现在我们给出一个数组,逻辑上看作一棵完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
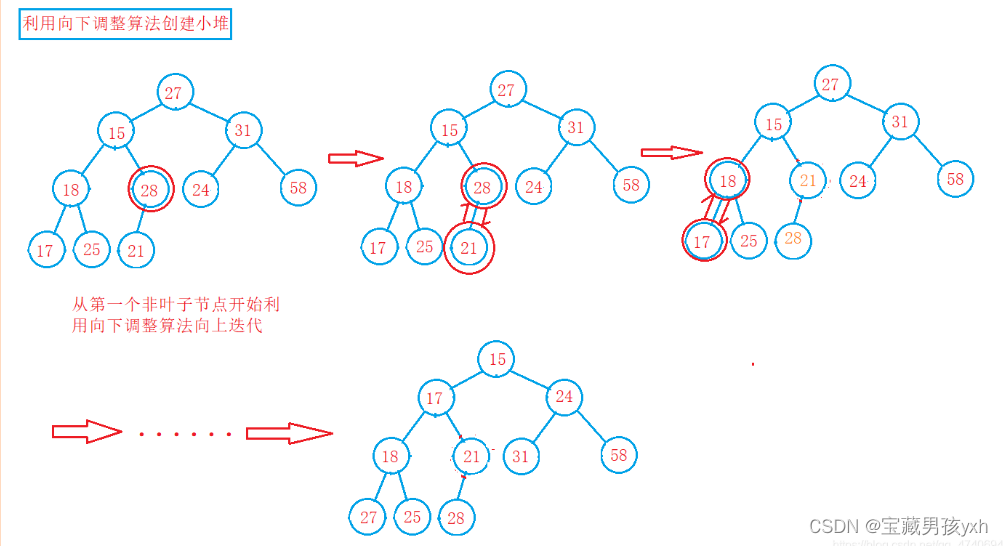
但是,使用向下调整算法需要满足一个前提:
若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
向下调整算法的基本思想(以建小堆为例):
1.从根结点处开始,选出左右孩子中值较小的孩子。
2.让小的孩子与其父亲进行比较。
若小的孩子比父亲还小,则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
若小的孩子比父亲大,则不需处理了,调整完成,整个树已经是小堆了。
代码如下:
//交换函数
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//堆的向下调整(小堆)
void AdjustDown(int* a, int n, int parent)
{//child记录左右孩子中值较小的孩子的下标int child = 2 * parent + 1;//先默认其左孩子的值较小while (child < n){if (child + 1 < n&&a[child + 1] < a[child])//右孩子存在并且右孩子比左孩子还小{child++;//较小的孩子改为右孩子}if (a[child] < a[parent])//左右孩子中较小孩子的值比父结点还小{//将父结点与较小的子结点交换Swap(&a[child], &a[parent]);//继续向下进行调整parent = child;child = 2 * parent + 1;}else//已成堆{break;}}
}
那么建堆的时间复杂度又是多少呢?
当结点数无穷大时,完全二叉树与其层数相同的满二叉树相比较来说,它们相差的结点数可以忽略不计,所以计算时间复杂度的时候我们可以将完全二叉树看作与其层数相同的满二叉树来进行计算。
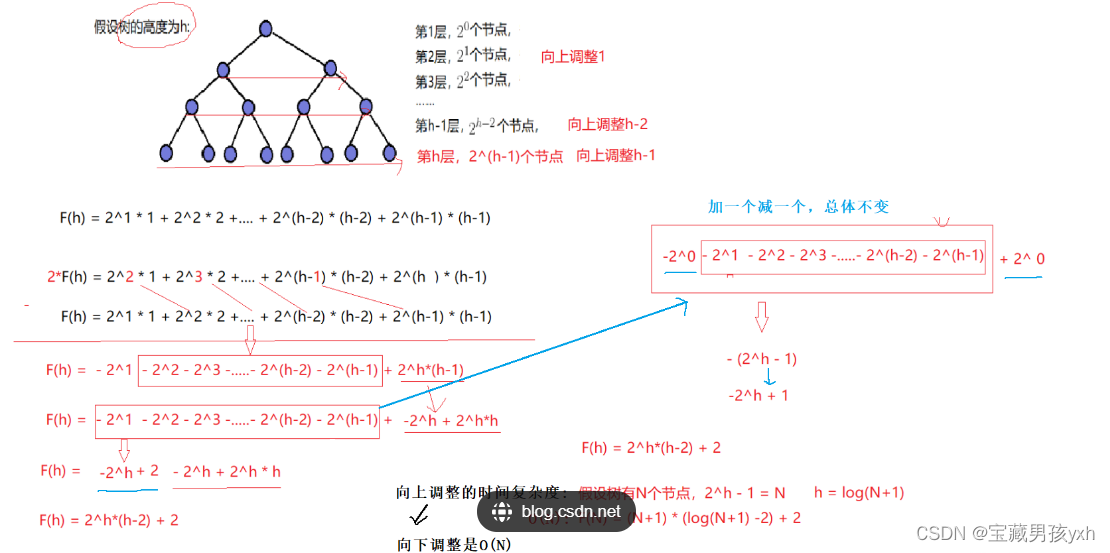
堆的向上调整算法
当我们在一个堆的末尾插入一个数据后,需要对堆进行调整,使其仍然是一个堆,这时需要用到堆的向上调整算法。
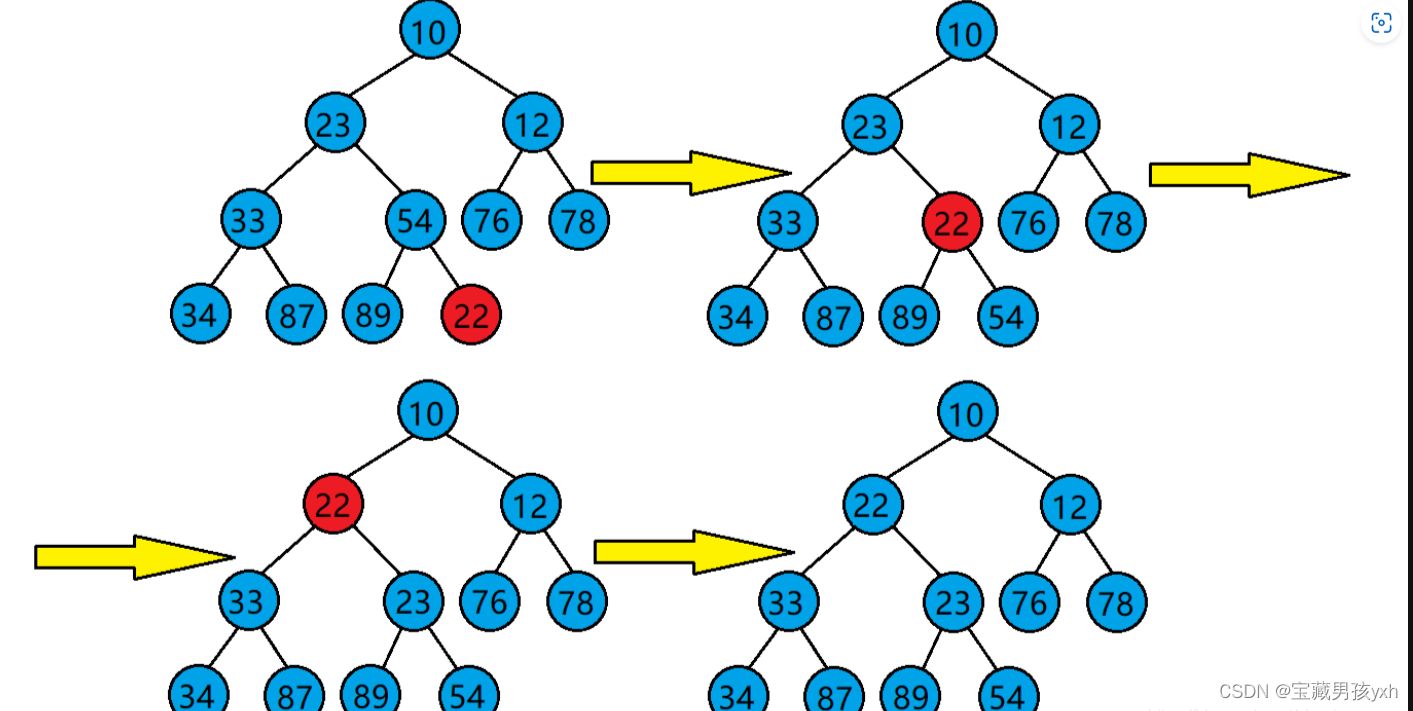
代码实现
//交换函数
void Swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}//堆的向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0)//调整到根结点的位置截止{if (a[child] < a[parent])//孩子结点的值小于父结点的值{//将父结点与孩子结点交换Swap(&a[child], &a[parent]);//继续向上进行调整child = parent;parent = (child - 1) / 2;}else//已成堆{break;}}
}
堆的实现
初始化堆
// 初始化堆
HeapNode* initializeHeap() {return nullptr; // 返回空指针表示空堆
}
判断堆是否为空
// 判断堆是否为空
bool isEmpty(HeapNode* heap) {return heap == nullptr;
}
这个函数简单地检查堆是否为空,如果堆是空的则返回true,否则返回false。
插入元素
// 向堆中插入元素
HeapNode* insertElement(HeapNode* heap, int val) {HeapNode* newNode = new HeapNode(val); // 创建新节点if (isEmpty(heap)) {return newNode; // 如果堆为空,新节点即为根节点} else {// 找到最后一个节点HeapNode* temp = heap;while (temp->left != nullptr && temp->right != nullptr) {temp = temp->left; // 堆是一个完全二叉树,所以优先插入左子节点}// 插入新节点作为最后一个节点的左子节点if (temp->left == nullptr) {temp->left = newNode;} else {temp->right = newNode;}return heap;}
}
这个函数首先创建一个新节点,然后判断堆是否为空。如果堆为空,新节点即为根节点。如果堆不为空,函数会找到最后一个节点,然后将新节点插入为其左子节点(优先插入左子节点)或右子节点。
删除元素
// 从堆中删除元素
HeapNode* deleteElement(HeapNode* heap, int val) {if (heap == nullptr) {std::cout << "Heap is empty." << std::endl;return heap; // 如果堆为空,直接返回}// 先找到要删除的节点及其父节点HeapNode* parent = nullptr;HeapNode* nodeToDelete = heap;while (nodeToDelete != nullptr && nodeToDelete->value != val) {parent = nodeToDelete;if (val < nodeToDelete->value) {nodeToDelete = nodeToDelete->left;} else {nodeToDelete = nodeToDelete->right;}}// 如果未找到要删除的节点if (nodeToDelete == nullptr) {std::cout << "Element not found in heap." << std::endl;return heap;}// 如果要删除的节点有两个子节点if (nodeToDelete->left != nullptr && nodeToDelete->right != nullptr) {// 找到要删除节点的右子树中最小的节点HeapNode* minRight = nodeToDelete->right;while (minRight->left != nullptr) {minRight = minRight->left;}// 用最小右节点的值替换要删除的节点的值nodeToDelete->value = minRight->value;// 删除最小右节点heap = deleteElement(heap, minRight->value);return heap;}// 如果要删除的节点是叶子节点或只有一个子节点if (nodeToDelete->left == nullptr) {if (parent != nullptr) {if (parent->left == nodeToDelete) {parent->left = nodeToDelete->right;} else {parent->right = nodeToDelete->right;}} else {heap = nodeToDelete->right;}delete nodeToDelete;return heap;}if (nodeToDelete->right == nullptr) {if (parent != nullptr) {if (parent->left == nodeToDelete) {parent->left = nodeToDelete->left;} else {parent->right = nodeToDelete->left;}} else {heap = nodeToDelete->left;}delete nodeToDelete;return heap;}return heap;
}
删除元素代码解释
这段代码实现了从堆中删除元素的功能。让我来解释一下:
-
首先,我们检查堆是否为空,如果为空则输出错误信息并直接返回。
-
接着,我们使用循环来找到要删除的节点以及其父节点。循环条件是当前节点不为空且当前节点的值不等于待删除的值,根据待删除的值和当前节点值的比较结果来决定往左子树还是右子树走。
-
如果我们找到了要删除的节点:
-
如果要删除的节点有两个子节点,则我们需要找到其右子树中的最小节点(即右子树中的最左下角的节点),将其值替换到待删除的节点中,然后递归地删除最小节点。
-
如果要删除的节点是叶子节点或只有一个子节点,则我们将其子节点链接到其父节点上,并删除待删除的节点。
-
-
最后,我们返回调整后的堆。
打印元素
// 打印堆中的元素
void printHeap(HeapNode* heap) {if (isEmpty(heap)) {std::cout << "Heap is empty." << std::endl;return;}// 使用中序遍历打印堆中的所有元素printHeap(heap->left);std::cout << heap->value << " ";printHeap(heap->right);
}
销毁堆
// 销毁堆
void destroyHeap(HeapNode* heap) {if (heap != nullptr) {destroyHeap(heap->left); // 递归销毁左子树destroyHeap(heap->right); // 递归销毁右子树delete heap; // 释放当前节点内存}
}
相关文章:

数据与结构--堆
堆 堆的概念 堆:如果有一个关键码的集合K{k0,k1,k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足ki<k2i1且ki<k2i2(或满足ki>k2i1且ki>k2i2),其中i0,1,2,…...
Github的使用教程(下载项目、寻找开源项目和上传项目)
根据『教程』一看就懂!Github基础教程_哔哩哔哩_bilibili 整理。 1.项目下载 1)直接登录到源码链接页或者通过如下图的搜索 通过编程语言对搜索结果进一步筛选。 如何去找开源项目:(Github 新手够用指南 | 全程演示&个人找项目技巧放…...
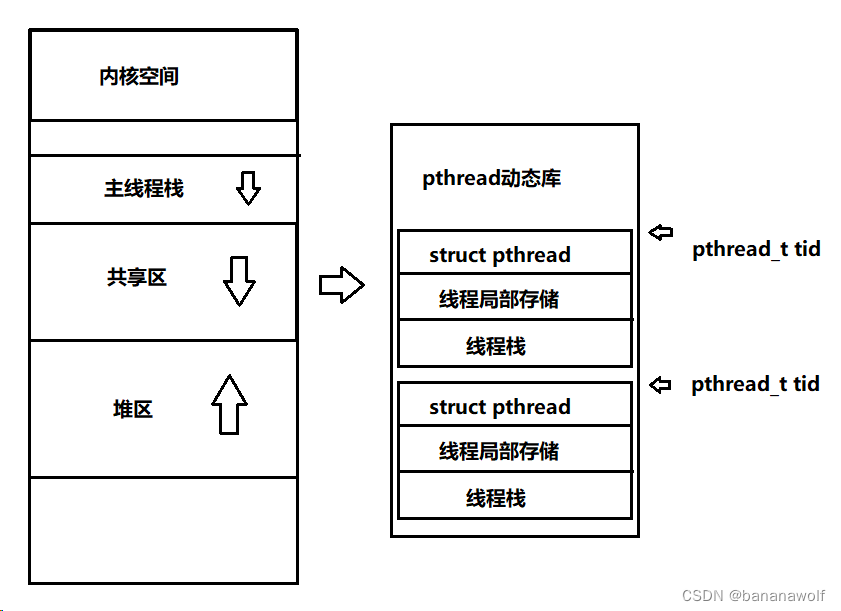
Linux-线程概念
1. 线程概念 线程:轻量级进程,在进程内部执行,是OS调度的基本单位;进程内部线程共用同一个地址空间,同一个页表,以及内存中的代码和数据,这些资源对于线程来说都是共享的资源 进程:…...

js的桶排序
桶排序(Bucket Sort)是一种分布式排序算法,它将元素分散到一系列桶中,然后对每个桶中的元素进行排序,并将所有的桶合并起来得到最终的排序结果。桶排序适用于输入的元素均匀分布在一个范围内的情况,它的时间…...
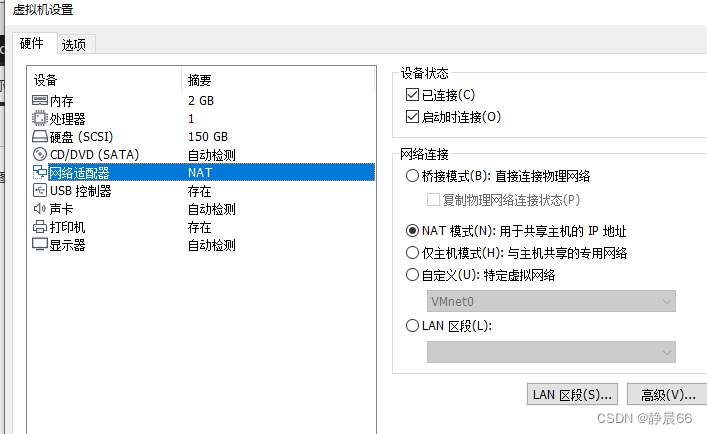
解决ubuntu无法上网问题
发现是网络配置成了Manual手动模式,现在都改成自动分配DHCP模式 打开后,尝试上网还是不行,ifconfig查看ip地址还是老地址,怀疑更改没生效,于是重启试试。 重启后,ip地址变了,可以打开网页了 …...

使用nvm管理多版本node.js
使用nvm(Node Version Manager)安装Node.js是一个非常方便的方法,因为它允许你在同一台机器上管理多个Node.js版本。以下是使用nvm安装Node.js的基本步骤: Linux 安装nvm 根据你的操作系统,安装命令可能会有所不同。以…...
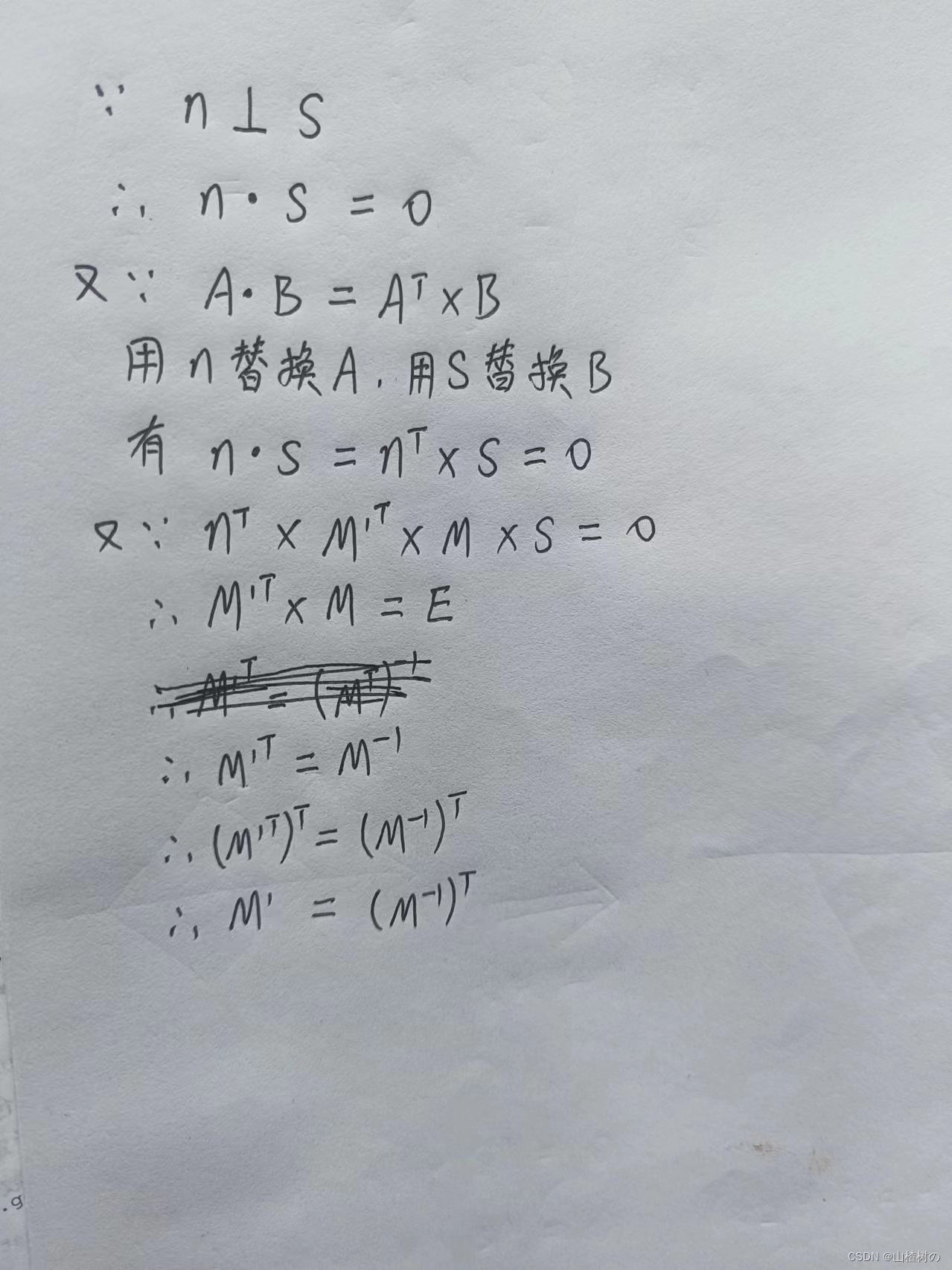
推导 模型矩阵的逆转置矩阵求运动物体的法向量
一个物体表面的法向量如何随着物体的坐标变换而改变,取决于变换的类型。使用逆转置矩阵,可以安全地解决该问题,而无须陷入过度复杂的计算中。 法向量变化规律 平移变换不会改变法向量,因为平移不会改变物体的方向。 旋转变换会改…...
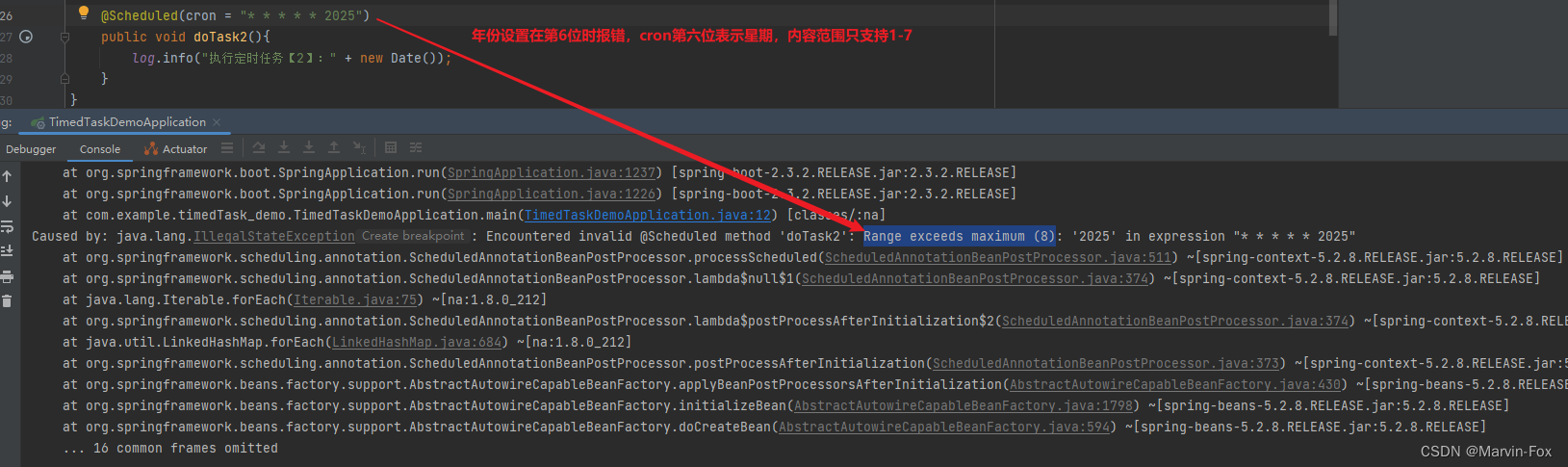
定时任务的几种实现方式
定时任务实现的几种方式: 1、JDK自带 (1)Timer:这是java自带的java.util.Timer类,这个类允许你调度一个java.util.TimerTask任务。使用这种方式可以让你的程序按照某一个频度执行,但不能在指定时间运行。…...

docker部署springboot+Vue项目
项目介绍:后台springboot项目,该项目环境mysql、redis 。前台Vue:使用nginx反向代理 方法一:docker run 手动逐个启动容器 1.docker配置nginx代理 将vue项目打包上传到服务器上。创建文件夹存储数据卷,html存放打包…...
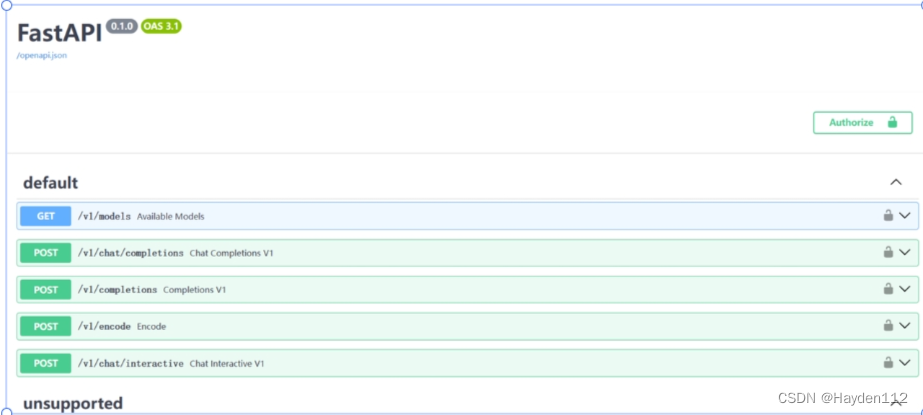
Llama3-Tutorial(Llama 3 超级课堂)-- 笔记
第1节—Llama 3 本地 Web Demo 部署 端口转发 vscode里面设置端口转发 https://a-aide-20240416-b4c2755-160476.intern-ai.org.cn/proxy/8501/ ssh -CNg -L 8501:127.0.0.1:8501 rootssh.intern-ai.org.cn -p 43681参考 https://github.com/SmartFlowAI/Llama3-Tutorial/b…...

【备战软考(嵌入式系统设计师)】12 - 嵌入式系统总线接口
我们嵌入式系统的总线接口可以分为两类,一类是并行接口,另一类是串行接口。 并行通信就是用多个数据线,每条数据线表示一个位来进行传输数据,串行接口就是一根数据线可以来一位一位地传递数据。 从上图也可以看出,并行…...

【一刷《剑指Offer》】面试题 18:树的子结构
力扣对应题目链接:LCR 143. 子结构判断 - 力扣(LeetCode) 牛客对应题目链接:树的子结构_牛客题霸_牛客网 (nowcoder.com) 核心考点:二叉树理解,二叉树遍历。 一、《剑指Offer》对应内容 二、分析问题 二叉…...
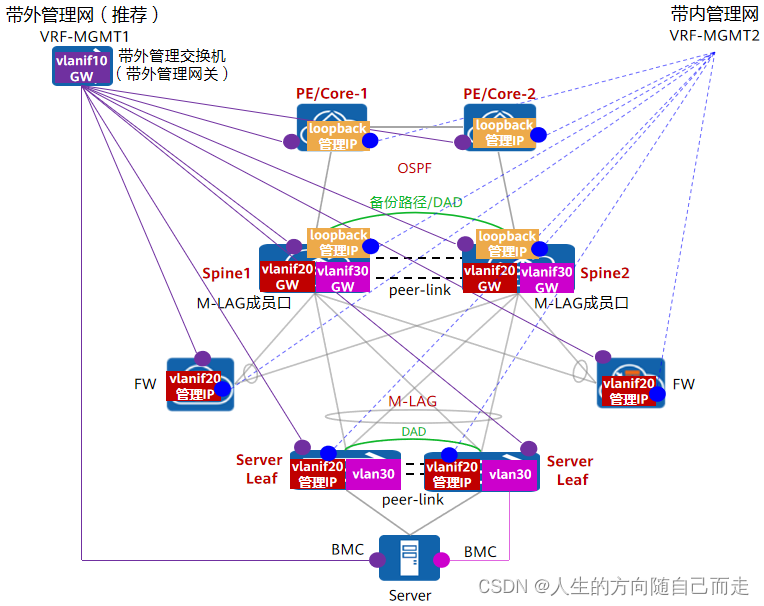
17 M-LAG 配置思路
16 华三数据中心最流行的技术 M-LAG-CSDN博客 M-LAG 配置思路 什么是M-LAG?为什么需要M-LAG? - 华为 (huawei.com) 1 配置 M-LAG 的固定的MAC地址 [SW-MLAG]m-lag system-mac 2-2-2 2 配置M-LAG 的系统标识符系统范围1到2 [SW-MLAG]m-lag system-nu…...

深入探索CSS3 appearance 属性:解锁原生控件的定制秘密
CSS3 的 appearance 属性,作为一个强大的工具,让我们得以细致入微地控制元素的外观,特别是对于那些具有平台特定样式的表单元素,如按钮、输入框等。本文不仅会深入解析 appearance 属性的基本工作原理和使用场景,还将通…...
 —— Dictionary类)
C# 集合(五) —— Dictionary类
总目录 C# 语法总目录 集合五 Dictionary 1. Dictionary 1. Dictionary 字典是键值对集合,通过键值对来查找 Dictionary和Hashtable的区别是Dictionary可以用泛型,而HashTable不能用泛型 OrderedDictionary 是按照添加元素时的顺序的字典,是…...
Java 函数式接口BiConsumer
BiConsumer是一个函数式接口,代表一个接受两个输入参数且不返回任何内容的操作符 import java.util.ArrayList; import java.util.List; import java.util.function.BiConsumer;public class BatchOperate<T> {private int batchSize3000;private List<T&…...
)
SWERC 2022-2023 - Online Mirror H. Beppa and SwerChat (双指针)
Beppa and SwerChat 题面翻译 B和她的怪胎朋友在某个社交软件上的聊天群聊天。 这个聊天群有包括B在内的n名成员,每个成员都有自己从1-n的独特id。 最近使用这个聊天群的成员将会在列表最上方,接下来较次使用聊天软件的成员将会在列表第二名࿰…...

四川汇昌联信:拼多多运营属于什么行业?
拼多多运营属于什么行业?这个问题看似简单,实则涉及到了电商行业的深层次理解。拼多多运营,顾名思义,就是在拼多多这个电商平台上进行商品销售、推广、客户服务等一系列活动。那么,这个行业具体包含哪些内容呢?下面就从四个不同…...

C++11 特性
总结 语法糖: 关键字: auto、decltype。nullptr。override、final。constexpr。语法: 基于范围的 for 循环。function 函数对象。 lambda 产生函数对象。bind 产生函数对象。目的:写代码更便捷、更严谨,让编译器做更多的事情。STL 容器: array。forward_list。unordered_…...

二、使用插件一键安装HybridCLR
预告 本专栏将介绍如何使用这个支持热更的AR开发插件,快速地开发AR应用。 专栏: Unity开发AR系列 插件简介 通过热更技术实现动态地加载AR场景,简化了AR开发流程,让用户可更多地关注Unity场景内容的制作。 热更方案 基于Hybri…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
