电商技术揭秘营销相关系列文章合集(4)

相关系列文章
电商技术揭秘相关系列文章合集(1)
电商技术揭秘相关系列文章合集(2)
电商技术揭秘相关系列文章合集(3)

文章目录
- 引言
- 集合说明
- 集合文章列表
引言
在数字化浪潮的推动下,电商行业正以前所未有的速度发展,而营销作为电商生态中的关键环节,其策略与技术的创新成为了决定电商企业成功与否的重要因素。从电商平台营销系统的构建,到营销策略的精心策划与实施,再到社交化营销、内容营销、智能广告投放等多维度的探索与实践,电商营销的边界在不断拓展,技术与应用也在持续演进。
近年来,随着社群营销与粉丝经济的兴起,电商营销又迈入了新的发展阶段。社群营销通过聚合具有共同兴趣或需求的用户群体,形成了强大的品牌影响力与传播力。
引言
在当今日益繁荣的电商时代,营销策略与技术创新的融合已经成为推动电商平台持续发展的关键动力。从基础的营销系统构建,到精细化的营销策略制定,再到社交化、内容化以及智能化的营销创新,每一步都凝聚着电商行业的智慧与努力。
集合说明
在过往的电商技术揭秘系列文章中,我们深入探讨了电商平台在营销领域的多个方面,包括营销系统的搭建、营销策略的运用、社交媒体的利用、社区的建设、内容营销的创新、智能广告投放与效果评估,以及个性化广告与投放策略等。这些文章不仅为我们揭示了电商平台在营销领域的丰富实践,也为我们展示了电商行业在营销策略和技术应用方面的不断创新和进步。
特别是在《电商核心技术揭秘53:社群营销与粉丝经济》及后续的文章中,我们详细探讨了社群营销与粉丝经济的重要性,以及如何将这两者有效结合以推动电商平台的增长。社群营销作为一种新兴的营销方式,通过构建和运营社群,实现了品牌与消费者之间的深度互动,而粉丝经济则通过挖掘和利用粉丝的价值,为品牌带来了更多的商业机会。
然而,随着市场竞争的加剧和消费者需求的不断变化,社群营销也面临着新的挑战和机遇。为了更好地应对这些挑战并抓住机遇,我们需要不断学习和探索社群营销的未来趋势和创新应用。
因此,本文旨在综合分析社群营销的未来趋势与挑战,为电商平台在社群营销领域的发展提供有价值的参考和启示。通过深入剖析社群营销的技术创新应用、可持续发展、伦理与法规挑战以及全球趋势等方面,我们希望能够为电商平台在社群营销领域的发展提供新的思路和方向。
集合文章列表
-
电商技术揭秘四十一:电商平台的营销系统浅析
-
电商技术揭秘四十二:电商平台营销策略浅析(上)
-
电商核心技术揭秘四十二:电商平台营销策略浅析(下)
-
电商核心技术揭秘四十四:营销与广告策略(上)
-
电商核心技术揭秘四十五:营销与广告策略(下)
-
电商核心技术揭秘四十六:社交化营销中的社交媒体平台浅析
-
电商核心技术揭秘四十七:社会化营销中的社区建设
-
电商核心技术揭秘四十七:社会化营销中的社区建设
-
电商核心技术揭秘四十八:内容营销浅析
-
电商核心技术揭秘四十九:智能广告投放与效果评估
-
电商核心内容揭秘50:个性化广告与投放策略
-
电商核心内容揭秘51:个性化广告与投放策略
-
电商核心技术揭秘52:数字化内容营销创新
-
电商核心技术揭秘53: 社群营销与粉丝经济
-
电商核心技术揭秘54: 粉丝经济的挖掘与利用
-
电商核心技术揭秘55: 社群与粉丝经济的结合
-
电商核心技术揭秘55: 社群营销的未来趋势与挑战
如上述文章对您有所帮助,建议您点赞收藏,以防后续迷失在知识的浩瀚大海之中…
相关文章:

电商技术揭秘营销相关系列文章合集(4)
相关系列文章 电商技术揭秘相关系列文章合集(1) 电商技术揭秘相关系列文章合集(2) 电商技术揭秘相关系列文章合集(3) 文章目录 引言集合说明集合文章列表 引言 在数字化浪潮的推动下,电商行…...

LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】
LeetCode-2391. 收集垃圾的最少总时间【数组 字符串 前缀和】 题目描述:解题思路一:处理垃圾和路程单独计算。解题思路二:逆向思维,计算多走的路解题思路三:只记录,当前t需要计算几次 题目描述:…...

再有人说数字孪生大屏没有用,用这8条怼回去。
数字孪生大屏之所以受到欢迎,主要有以下几个原因: 实时数据可视化 数字孪生大屏可以将实时数据以直观的可视化形式展示出来,让用户能够一目了然地了解数据的状态和趋势。这样可以帮助用户更好地理解和分析数据,及时做出决策和调…...
蓝桥杯练习系统(算法训练)ALGO-946 Q神的足球赛
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 足球赛上,只见Q神如闪电般的速度带球时而左,时而右,时而前,时而后ÿ…...

【Android】Kotlin学习之Kotlin方法的声明和传参
方法声明 普通类的方法 静态类的方法 不需要构建实例对象, 可以通过类名直接访问静态方法 : NumUtil.double(1) companion object 伴生类的方法 使用companion object 在普通类里定义静态方法 参数 括号内传入方法 : 当参数是方法时, 并且是最后一个参数 , 可以使用括号外…...
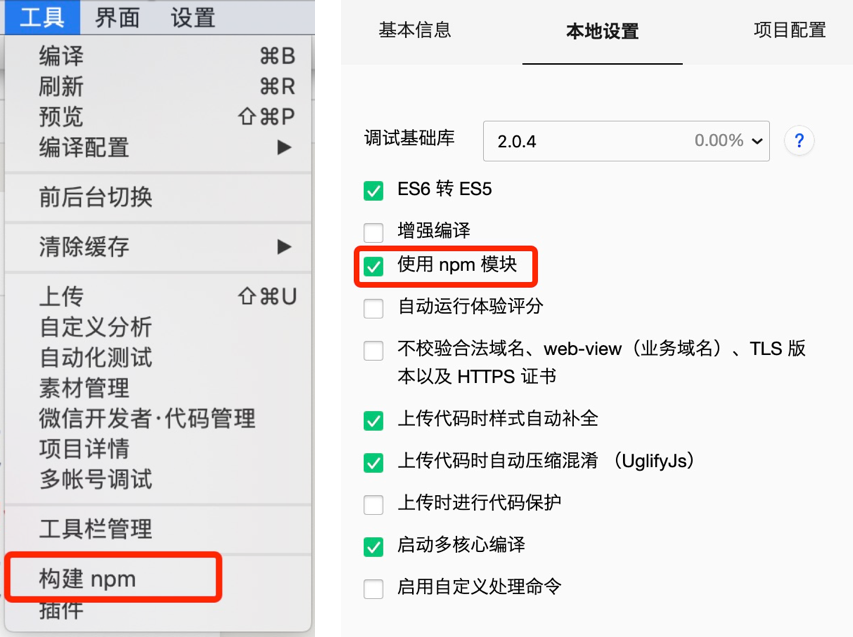
微信小程序 17:小程序使用 npm 包和组件应用
目前,小程序中已经支持实用 npm 安装第三方包,从而提高小程序的开发效率,但是在小程序中使用 npm 包有三个限制: 不支持 Node.js内置库的包不支持依赖于浏览器内置对象的包不支持依赖于 C插件的包 Vant Weapp Vant Weapp是有赞…...
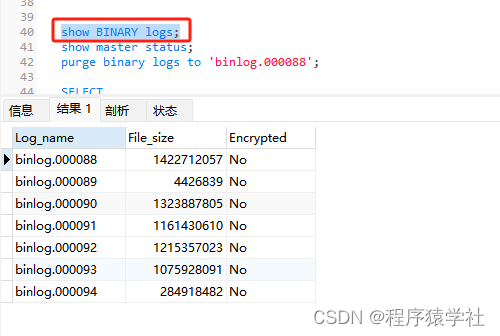
【mysql篇】执行delete删除大量数据后,磁盘未清空,为什么?
目录 迁移脚本删除数据以及备份数据 解决方法OPTIMIZE TABLE二进制日志按月生成数据 最近某个项目虽说用户量不大,但是,单表的数据量越来越大,mysql一般单表超过千万级别后,性能直线下降,所以利用shardingphere按月做了…...

【Qt 学习笔记】Qt常用控件 | 多元素控件 | Tree Widget的说明及介绍
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt常用控件 | 多元素控件 | Tree Widget的说明及介绍 文章编号&#x…...
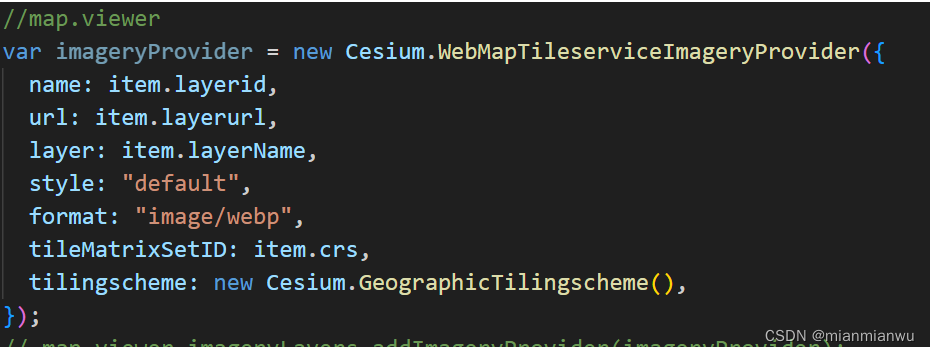
在Mars3d实现cesium的ImageryLayer自定义瓦片的层级与原点
需要自定义瓦片层级和原点,所以需要自己写第三方图层,但是之前写的很多方法,图层控制和显隐以及透明度,需要跟之前的交互一直,改动量太大的话不划算,所以直接看Mars3d的layer基类,把重写的image…...

logback日志持久化
1、问题描述 使用logback持久化记录日志。 2、我的代码 logback是Springboot框架里自带的,所以只要引入“spring-boot-starter”就行了。无需额外引入logback依赖。 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns&…...
、函数定义(Function Definition)和函数声明(Function Declaration))
函数原型(Function Prototype)、函数定义(Function Definition)和函数声明(Function Declaration)
函数原型(Function Prototype)、函数定义(Function Definition)和函数声明(Function Declaration)在C和C等编程语言中扮演着不同的角色,但它们有时在概念上可能会有些重叠。下面是它们之间的主要…...

Go有无缓冲channel的区别
无缓冲的channel channel的默认类型就是无缓冲的。当一个数据被发送到无缓冲的channel中,发送操作会被阻塞,知道有另一个goroutine从这个channel中接收这个数据。同样,当试图从一个无缓冲的channel中接收数据时,如果没有数据可以…...
【全开源】Fastflow工作流系统(源码搭建/上线/运营/售后/维护更新)
一款基于FastAdminThinkPHP开发的可视化工作流程审批插件,帮助用户基于企业业务模式和管理模式自行定义所需的各种流程应用,快速构建企业自身的流程管控体系,快速融合至企业协同OA办公系统。 提供全部无加密服务端源码和前端源代码࿰…...

超越传统游戏:生成式人工智能对游戏的变革性影响
人工智能(AI)在游戏中的应用 游戏产业是一个充满活力、不断发展的领域,人工智能(AI)的融入对其产生了重大影响。这一技术进步彻底改变了游戏的开发、玩法和体验方式。本文分析的重点是传统人工智能和生成式人工智能在游…...

SpringCloud微服务之Eureka、Ribbon、Nacos详解
SpringCloud微服务之Eureka、Ribbon、Nacos详解 1、认识微服务1.1、单体架构1.2、分布式架构1.3、微服务1.4、SpringCloud 2、服务拆分与远程调用2.1、服务拆分的原则2.2、服务拆分示例2.2、提供者与消费者 3、Eureka注册中心3.1、Eureka的结构和作用3.2、搭建eureka-server3.2…...
五角钱的程序员 | Kafka 是什么?
本文来源公众号“五角钱的程序员”,仅用于学术分享,侵权删,干货满满。 原文链接:Kafka 是什么? 你是一个程序员,假设你维护了两个服务 A 和 B。B 服务每秒只能处理 100 个消息,但 A 服务却每秒…...

C++中合成的默认构造函数的访问权限
问题 我们知道,在C中,如果没有为一个类显式定义构造函数,那么编译器会为我们隐式地定义一个默认构造函数。那么,你有没有想过,这个隐式定义的默认构造函数(合成的默认构造函数)的访问权限是什么…...
【前端】桌面版docker并部署前端项目
环境 win10专业版 2004 , 需科学 官网下载安装包并安装4.29.0版本 终端输入 wsl --installdocker桌面版和模拟器只能选一个,不然一直转圈圈 镜像配置加速,在settings—>docker engine下 {"builder": {"gc": {"defaultKee…...

发布GPT-5的方式可能会与以往不同;开源vocode使用 AI 自动拨打电话;开源gpt智能对话客服工具;AI自动写提示词
✨ 1: vocode 用AI通过声音与用户进行实时交流 Vocode是一个旨在帮助开发者快速构建基于声音的大型语言模型(LLM)应用程序的开源库。简单来说,如果你想要开发一个能够通过声音与用户进行实时交流的应用,比如电话机器人、语音助手…...
)
Linux 作业管理 (bg, fg, jobs, kill)
bg 和 fg 是用来管理作业(在 Unix/Linux 命令行下运行的进程)的命令。 1. bg 命令 bg 命令用于将作业(job)放到后台运行。当你在终端中运行一个命令或程序时,它会占用当前终端的控制,如果你想让这个任务在…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
