vue3引入vant完整步骤
在Vue 3中引入Vant(一个基于Vue的移动端UI组件库)的完整步骤通常包括以下几个部分:
-
安装Vue CLI(如果你还没有安装的话):
npm install -g @vue/cli
- 创建一个新的Vue项目:
假设你希望项目名为my-vant-project。
vue create my-vant-project
在创建项目时,你可以选择你需要的配置(例如,Babel, Router, Vuex等)。
3. 安装Vant:
由于你使用的是Vue 3,你需要安装与Vue 3兼容的Vant版本。
npm install vant@next --save
这里的@next表示安装的是Vant的下一个主要版本(即Vue 3兼容的版本)。
4. 按需引入(可选,但推荐):
为了减少打包体积,你可能希望只引入你实际需要的Vant组件。为此,你可以使用babel-plugin-import插件来实现按需引入。
首先,安装该插件:
npm install babel-plugin-import --save-dev
然后,在你的babel.config.js文件中配置该插件:
module.exports = { presets: [ '@vue/cli-plugin-babel/preset' ], plugins: [ ['import', { libraryName: 'vant', libraryDirectory: 'es', style: true }, 'vant'] ] };
现在,你可以在你的Vue组件中按需引入Vant组件了。例如,如果你想要引入Button组件,你可以这样做:
import { Button } from 'vant'; // 在你的组件中使用Button...
- 在你的项目中使用Vant:
在你的Vue组件中,你可以开始使用你已经引入的Vant组件了。确保在你的组件中正确地注册和使用它们。
(可选)配置PostCSS和rem单位:
如果你想要使用Vant的某些组件,并希望使用rem单位而不是px单位,你可能需要安装和配置一些PostCSS插件。但这不是必须的,取决于你的具体需求。
以上就是在Vue 3中引入Vant的完整步骤。希望这对你有所帮助!
相关文章:

vue3引入vant完整步骤
在Vue 3中引入Vant(一个基于Vue的移动端UI组件库)的完整步骤通常包括以下几个部分: 安装Vue CLI(如果你还没有安装的话): npm install -g vue/cli 创建一个新的Vue项目: 假设你希望项目名为my…...

C语言——文件缓冲区
一、用户缓冲区和系统缓冲区 缓冲区的概念确实可以分为多个层次,其中最常见的两个层次是用户缓冲区和系统缓冲区。 这里的用户缓冲区和系统缓冲区都包括输入输出缓冲区。 1、用户缓冲区(User-space Buffer) 用户缓冲区是指由用户程序&…...
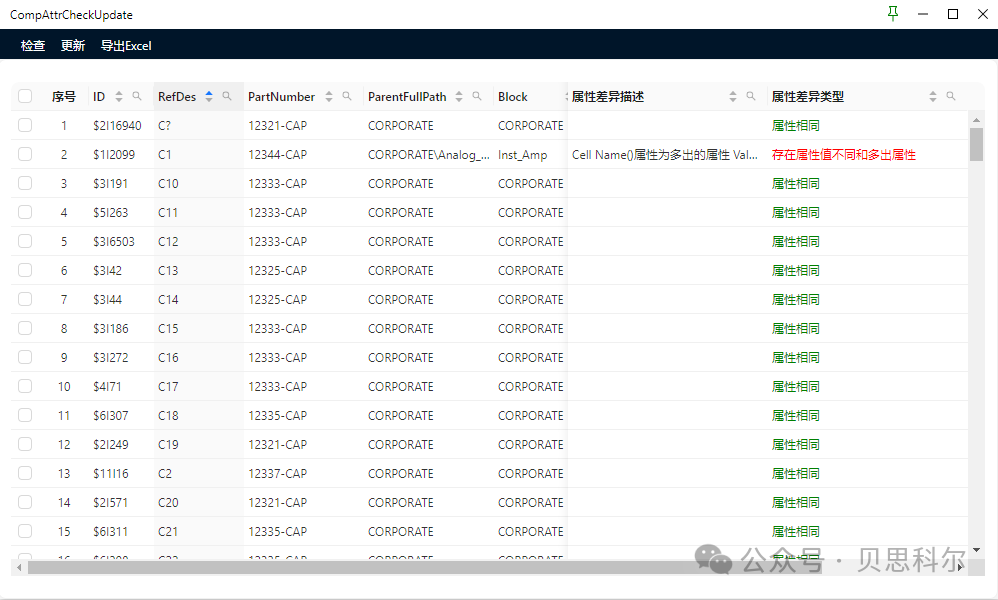
如何快速检测原理图中的元器件与PLM系统的一致性,提高原理图设计准确性
背景介绍 保证原理图中的元器件来源于公司的PLM系统、ERP系统的,是输出有效BOM的根源,初始BOM的准确率,能大大降低ECN的数量,提高生产备料的时效,缩短采购周期。 然而,原理图设计过程中,由于…...

英特尔处理器排行
英特尔的处理器性能排行通常是根据其发布的不同代数和型号来划分的,以下是一些高性能的英特尔处理器: Intel 酷睿 i9 14900K:这是目前英特尔桌面平台中的旗舰处理器之一,提供了极高的性能,适合高端游戏和专业工作负载…...

【日志革新】在ThinkPHP5中实现高效TraceId集成,打造可靠的日志追踪系统
问题背景 最近接手了一个骨灰级的项目,然而在项目中遇到了一个普遍的挑战:由于公司采用 ELK(Elasticsearch、Logstash、Kibana)作为日志收集和分析工具,追踪生产问题成为了一大难题。尽管 ELK 提供了强大的日志分析功…...
)
英译汉早操练-(二十)
hello大家好,这篇跟随十九,继续真题学习。如果想看全部请返回到第十九篇。 英译汉早操练-(十九)-CSDN博客 The political upheaval in Libya and elsewhere in North Africa has opened the way for thousands of new migrants to…...
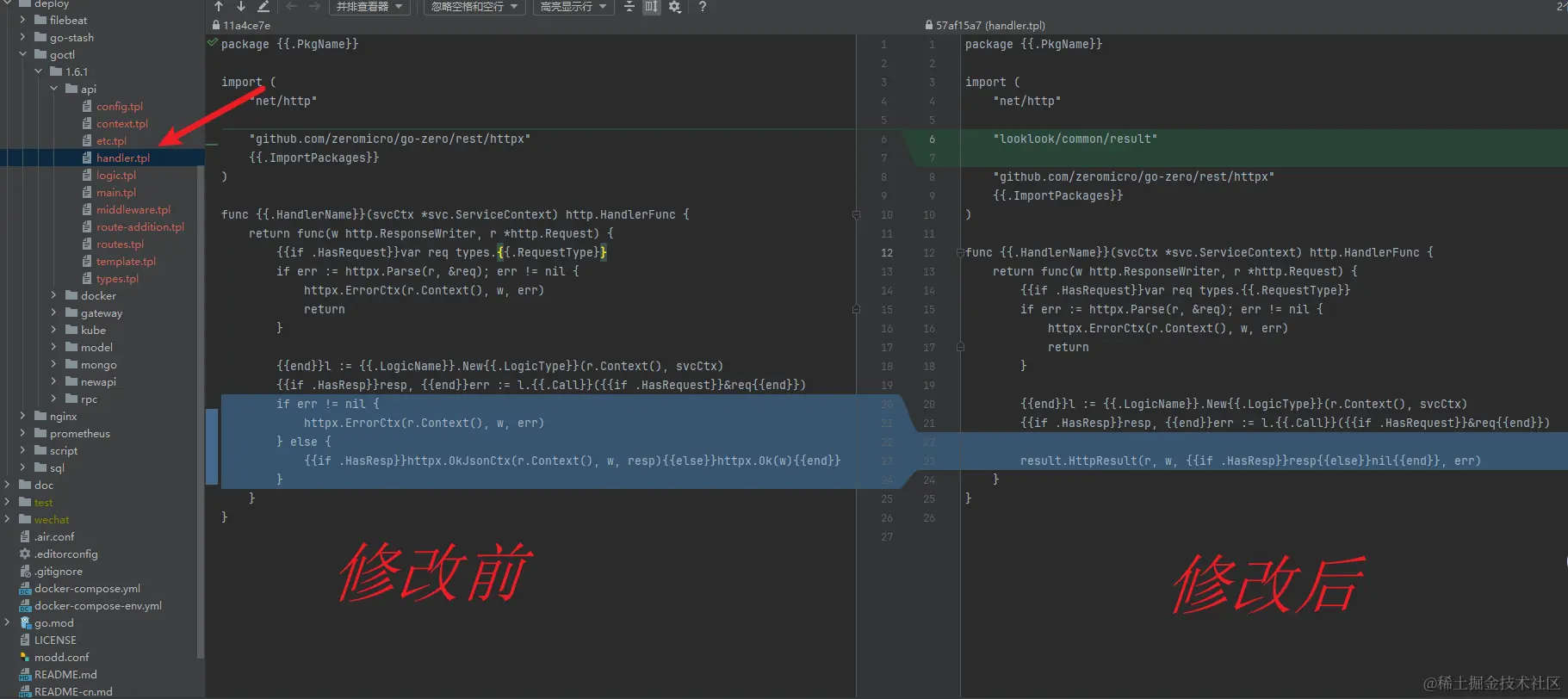
Go-Zero自定义goctl实战:定制化模板,加速你的微服务开发效率(四)
前言 上一篇文章带你实现了Go-Zero和goctl:解锁微服务开发的神器,快速上手指南,本文将继续深入探讨Go-Zero的强大之处,并介绍如何使用goctl工具实现模板定制化,并根据实际项目业务需求进行模板定制化实现。 通过本文…...

(五)STM32F407 cubemx IIC驱动OLED(1)IIC协议篇
(五)STM32F407 cubemx IIC驱动OLED(1)IIC协议篇 这篇文章主要是个人的学习经验,想分享出来供大家提供思路,如果其中有不足之处请批评指正哈。 废话不多说直接开始主题,本人是基于STM32F407V…...

OpenCV特征匹配总结
1.概述 在深度学习出现之前,图像中的特征匹配方法主要有 2.理论对比 3.代码实现 #include <iostream> #include <opencv2/opencv.hpp>int main(int argc, char** argv) {if(argc ! 3) {std::cerr << "Usage: " << argv[0] <…...
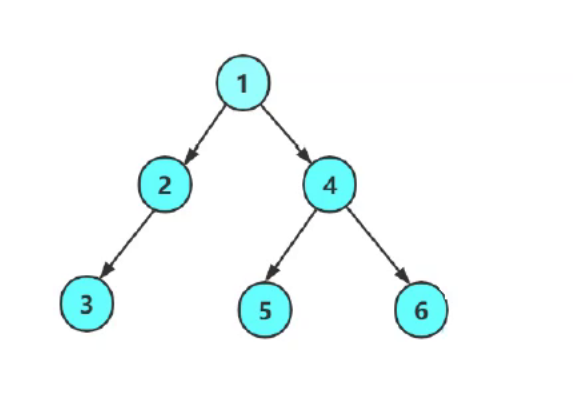
二叉树的四种遍历代码实现
二叉树的遍历大致能分为以下几种 1.前序:根 左 右 2.中序:左 根 右 3.后序:左 右 根 4.层序:从根开始一层一层的向下 如上图访问顺序: 前序:1 2 3 N N N 4 5 N N 6 N N 中序:N 3 N 2 N 1 N 5 N 4 N …...

系统和功能测试:确保软件的功能和易用性
目录 概述 功能测试 LOSED 模型 用例的设计 等价类划分 边界值分析 循环结构测试的综合方法 因果图 决策表 功能图 正交实验设计 易用性测试 内部易用性测试 外部易用性测试 功能性测试 正向功能性测试 负向功能性测试 功能性测试工具 结语 概述 在软件开发…...

关于服务端接口知识的汇总
大家好,今天给大家分享一下之前整理的关于接口知识的汇总,对于测试人员来说,深入了解接口知识能带来诸多显著的好处。 一、为什么要了解接口知识? 接口是系统不同模块之间交互的关键通道。只有充分掌握接口知识,才能…...
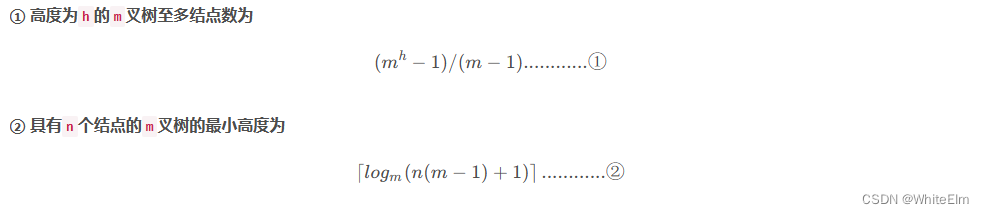
树(数据结构)
树的定义 一个根结点,其余结点分为 m 个不相交的集合, 其中每个集合本身又是一棵树,并且称为根的子树。 树的根结点没有前驱,其他结点有且仅有一个前驱。 所有结点可以有0个或多个后继。 基本术语 结点的度 树的度 : 树…...
Spring底层入门(十一)
1、条件装配 在上一篇中,我们介绍了Spring,Spring MVC常见类的自动装配,在源码中可见许多以Conditional...开头的注解: Conditional 注解是Spring 框架提供的一种条件化装配的机制,它可以根据特定的条件来控制 Bean 的…...
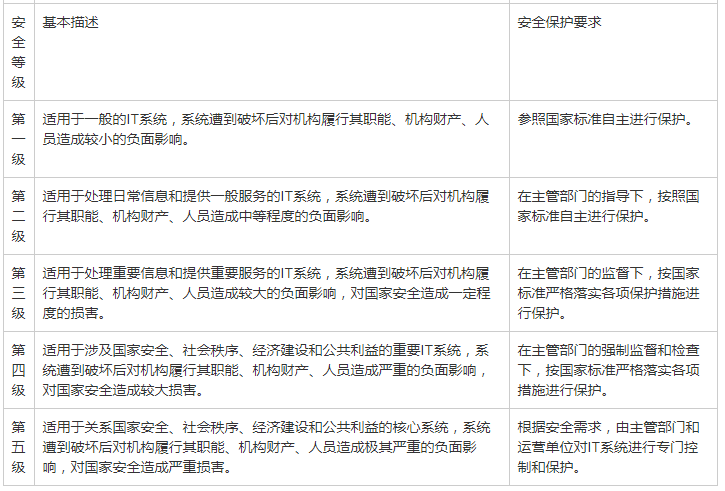
优质资料:大型制造企业等级保护安全建设整改依据,系统现状分析,网络安全风险分析
第1章 项目概述 XX 大型制造型企业是国内一家大型从事制造型出口贸易的大型综合企业集团,为了落实国家及集团的信息安全等级保护制度,提高信息系统的安全防护水平,细化各项信息网络安全工作措施,提升网络与信息系统工作的效率&am…...

几种监控工具学习
在Linux上有很多监控工具,比如Zabbix、Prometheus、APM和ELK 监控工具是确保系统稳定运行的关键组件之一,它可以帮助系统管理员和开发人员及时发现并解决问题。 以下是几种流行的监控工具的简要介绍: Zabbix: Zabbix 是一个企…...

树莓派python开发
树莓派自带thonny 点亮LED灯 import RPi.GPIO as GPIO import time# 设置GPIO模式为BCM GPIO.setmode(GPIO.BCM)# 设置LED引脚 led_pin 18# 设置LED引脚为输出 GPIO.setup(led_pin, GPIO.OUT)# 点亮LED GPIO.output(led_pin, GPIO.HIGH)# 延时2秒 time.sleep(2)# 关闭LED GPI…...

纯血鸿蒙APP实战开发——首页下拉进入二楼效果案例
介绍 本示例主要介绍了利用position和onTouch来实现首页下拉进入二楼、二楼上划进入首页的效果场景,利用translate和opacity实现动效的移动和缩放,并将界面沉浸式(全屏)显示。 效果图预览 使用说明 向下滑动首页页面超过触发距…...
苹果cms:开启高速缓存加快访问速度
由于苹果cms采集的影片数据过多,如果不设置缓存,可能会造成网站访问缓慢,或者CPU消耗过高。随着用户访问量的上升,添加缓存设置是有这个必要的。目前cms提供了四种缓存方式 1)file:以文件形式,通俗说直接访问Mysql,要达…...

实时数据推送——长轮询,短轮询,长连接
短轮询 短轮询是最简单的一种数据推送方式,客户端在固定的时间间隔(例如每隔5秒)向服务器发送请求,询问是否有更新的数据。服务器立即处理请求并返回数据,不论数据是否真的已经更新。 长轮询 长轮询是对短轮询的改进…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
