人才培养计划大纲
构建全面而高效的人才培养规划
文章大纲:
- 引言
- 人才培养的重要性
- 当前人才培养面临的挑战
- 文章目的与结构
- 人才培养规划的基本概念
- 定义与内涵
- 人才培养规划与企业战略的关系
- 人才培养规划的基本原则
- 人才培养规划的现状分析
- 当前人才培养规划的实践情况
- 存在的问题与不足
- 案例分析:成功与失败的经验
- 人才培养规划的策略制定
- 明确人才培养目标
- 制定人才培养策略
- 设定人才培养的阶段性目标
- 人才培养策略的评估与调整
- 人才培养的具体实施
- 选拔与招聘优秀人才
- 设计培训体系与课程
- 实施多元化的培养方式
- 激励机制与绩效评估
- 人才培养规划的支持系统
- 组织文化与价值观
- 领导力发展与团队建设
- 信息技术在人才培养中的应用
- 资金投入与资源配置
- 人才培养规划的风险管理与持续改进
- 识别与评估人才培养风险
- 制定风险管理策略
- 人才培养规划的持续改进
- 构建学习型企业
- 结论
- 总结文章要点
- 强调人才培养规划的重要性
- 对未来的展望
部分内容示例(第4部分:人才培养规划的策略制定)
4. 人才培养规划的策略制定
在制定人才培养规划的策略时,企业必须首先明确人才培养的目标。这些目标应当与企业的整体战略紧密相连,确保人才培养工作能够为企业的发展提供有力支持。
接下来,企业需要制定具体的人才培养策略。这些策略应当考虑到企业内部的资源条件、外部环境的变化以及员工的个人发展需求。例如,对于新员工,企业可以采取“导师制”或“轮岗制”等方式,帮助他们快速融入企业文化,掌握基本的工作技能;对于中层管理者,企业可以组织领导力培训、项目管理等进阶课程,提升他们的管理能力和团队协作能力;对于高层领导者,企业则需要注重培养他们的战略眼光和决策能力。
除了制定具体的培养策略外,企业还需要设定人才培养的阶段性目标。这些目标应当具有可衡量性、可达成性和挑战性,以便企业能够定期对人才培养工作进行评估和调整。
最后,企业需要建立人才培养策略的评估与调整机制。通过收集员工反馈、分析绩效数据等方式,企业可以了解人才培养策略的实施效果,及时发现并解决问题。同时,企业还需要根据外部环境的变化和企业内部的发展需求,对人才培养策略进行持续的优化和调整。
(注:以上仅为部分内容示例,实际撰写时需根据大纲进一步展开和细化。)
人才培养的重要性不言而喻,它是任何组织、国家乃至整个社会持续发展的关键。以下是关于人才培养重要性的详细阐述:
-
推动组织发展:人才是组织最宝贵的资源。优秀的人才能够带来创新的思维、高效的工作方法和卓越的业绩,从而推动组织不断向前发展。通过培养人才,组织能够建立起一支高素质、高技能、高效率的队伍,为组织的长期发展奠定坚实的基础。
-
增强竞争力:在激烈的市场竞争中,拥有高素质人才的企业往往能够占据优势地位。这些人才具备独特的专业技能和丰富的经验,能够为企业带来更多的机会和资源,增强企业的竞争力。因此,通过人才培养,企业能够不断提升自身的竞争力,在市场中立于不败之地。
-
促进个人成长:人才培养不仅有助于组织的发展,还能够促进个人的成长。通过培训、学习和实践,个人能够不断提升自己的能力和素质,实现自我价值的最大化。同时,个人在成长过程中也能够积累更多的经验和资源,为未来的职业发展打下坚实的基础。
-
推动社会进步:人才培养是推动社会进步的重要力量。优秀的人才能够为社会带来更多的创新成果和科技进步,推动社会的不断向前发展。同时,他们还能够为社会培养出更多的高素质人才,形成良性循环,推动整个社会不断向前进步。
-
应对挑战和变革:在快速变化的时代背景下,企业和组织面临着越来越多的挑战和变革。通过人才培养,企业和组织能够培养出具备适应能力和创新能力的人才,使他们能够迅速应对各种挑战和变革,保持竞争优势。
-
传承企业文化:人才培养还有助于传承企业文化。通过培训和教育,新员工能够更快地了解企业的历史、文化和价值观,从而更快地融入企业。同时,老员工也能够通过培训和学习不断更新自己的知识和技能,保持与企业的同步发展。这有助于企业文化的传承和发扬。
-
提升团队凝聚力:通过人才培养,企业和组织能够建立起一个高效、协作、创新的团队。团队成员之间能够相互学习、相互支持、相互信任,形成强大的团队凝聚力。这种凝聚力能够激发团队成员的积极性和创造力,提升整个团队的绩效和效率。
综上所述,人才培养对于组织、个人以及整个社会都具有重要的意义。因此,我们应该重视人才培养工作,加大投入力度,不断提高人才培养的质量和效果。
当前人才培养面临的挑战是多方面的,这些挑战不仅来自于教育环境、资源分配,还涉及到技能需求的变化、评估与反馈机制的有效性,以及全球化和技术革新的影响。以下是一些具体的挑战:
-
教育资源不均衡:在一些发展不平衡的地区,教育资源匮乏,学校条件差,师资力量不足,这导致了人才培养的不公平性。这使得一些地区的人才难以获得优质的教育资源,限制了他们的发展潜力。
-
教育体制僵化:传统的教育体制往往过于注重死记硬背,忽视了学生的创新能力和实践能力。这导致了许多学生在面对实际问题时缺乏独立思考和解决问题的能力。为了应对这一挑战,我们需要改革教育体制,注重培养学生的创新精神和实践能力。
-
技能需求与人才培养不匹配:随着科技的迅速发展和市场的变化,企业对人才的需求也在不断变化。然而,许多教育机构和企业在培养人才时往往没有及时更新技能需求,导致人才的技能与企业实际需求不一致。这造成了人才浪费和培养资源的浪费。为了解决这一问题,我们需要密切关注市场动态和技术发展趋势,及时调整人才培养方案和课程内容。
-
评估与反馈机制不完善:在人才培养过程中,有效的评估和反馈机制对于员工的成长至关重要。然而,许多企业缺乏有效的评估体系,无法准确衡量培训成果。此外,一些企业也缺乏及时的反馈机制,无法为员工提供有针对性的指导和建议。这限制了员工的成长和发展。为了应对这一挑战,我们需要建立完善的评估体系和反馈机制,确保员工能够得到及时的指导和支持。
-
人才流失问题:在竞争激烈的社会中,人才流失是一个不可避免的问题。许多企业面临着优秀人才的流失风险,这不仅影响了企业的运营和发展,也浪费了企业的培养资源。为了留住人才,我们需要为人才提供更多的发展机会和空间,让他们在自己的领域中得到更好的发展。同时,我们也需要关注员工的职业规划和发展需求,为他们提供更好的职业发展和晋升路径。
-
全球化和技术革新的挑战:随着全球化的深入发展和技术的不断进步,人才培养面临着更多的挑战。企业需要具备跨文化交流和合作的能力,以应对全球化带来的挑战。同时,技术的革新也使得企业需要不断更新知识和技能,以适应新的市场需求和技术变化。为了应对这些挑战,我们需要注重培养员工的跨文化交流能力和技术创新能力。
综上所述,当前人才培养面临的挑战是多方面的,我们需要从教育资源、教育体制、技能需求、评估与反馈机制、人才流失以及全球化和技术革新等方面入手,采取有效措施应对这些挑战,以提升人才培养的质量和效果。
相关文章:

人才培养计划大纲
构建全面而高效的人才培养规划 文章大纲: 引言 人才培养的重要性当前人才培养面临的挑战文章目的与结构人才培养规划的基本概念 定义与内涵人才培养规划与企业战略的关系人才培养规划的基本原则人才培养规划的现状分析 当前人才培养规划的实践情况存在的问题与不足…...

多语言环境下的正则表达式实战:校验整数、小数
在软件开发中,正则表达式是验证用户输入数据格式的强大工具,特别是在处理表单验证时。本文将通过JavaScript、Java、Python、C、Rust、Go、C六种编程语言展示如何使用正则表达式来校验输入是否为整数或小数,特别强调小数点后最多保留两位的场…...

过拟合和欠拟合的学习
1.什么拟合 就是说这个曲线能不能很好地描述某些样本数据,并且拥有较好的泛化能力。 2.什么是过拟合 过拟合就是曲线太过于贴切训练数据的特征了,在训练集上表现得非常优秀,近乎完美的预测/区分了所有得数据,但是在新的测试集上…...
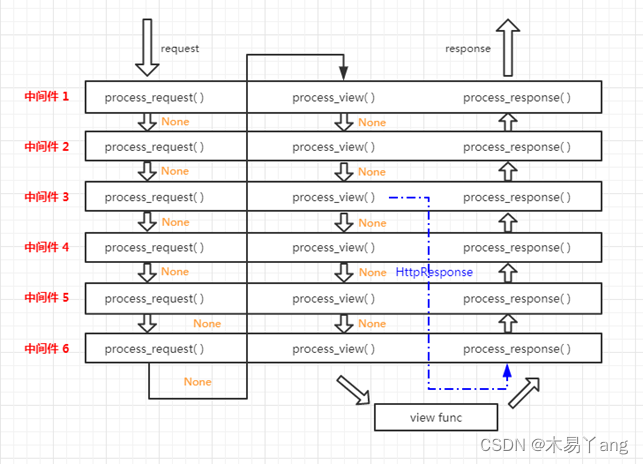
中间件的使用
中间件是全局使用 工厂函数定义中间件 middleware.py # 工厂函数的中间件 def simple_middleware(get_response):def middleware(request):print("在视图函数处理之前执行、、、、、")response get_response(request)print("在视图函数处理之后执行。。。。…...
阿里云OSS权限开通步骤及最佳实践
在阿里云云计算平台中,对象存储服务(OSS)是一种高度可扩展的云存储服务,提供了安全、可靠、低成本的数据存储解决方案。在使用OSS时,正确配置权限是至关重要的,以确保数据的安全性和访问控制。本文将介绍阿…...

【Python贪吃蛇】:编码技巧与游戏设计的完美结合
文章目录 🔥一、运行效果💥二、游戏教程✈1. 导入模块❤️2. 初始化游戏元素☔3. 改变蛇移动的方向👊4. 绘制方块🚀5. 检查蛇头是否在游戏区域内🌈6. 定义蛇的移动函数🎬7. 绑定键盘事件 ⭐三、完整代码 &a…...
2024.5.19 机器学习周报
引言 Abstract 文献阅读 1、题目 X-HRNET: TOWARDS LIGHTWEIGHT HUMAN POSE ESTIMATION WITH SPATIALLY UNIDIMENSIONAL SELF-ATTENTION 2、引言 高分辨率表示是人体姿态估计实现高性能所必需的,随之而来的问题是高计算复杂度。特别地,主要的姿态估…...

母亲节祝福html源码示例
创建一个完整的HTML页面,我可以为您提供一个简单的HTML模板,其中包含一些示例性的祝福语,并添加一些注释以帮助您理解如何扩展内容。 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8&qu…...

微信小程序开发中的权限管理与用户身份验证:守护数据安全与用户体验
微信小程序开发中的权限管理与用户身份验证:守护数据安全与用户体验 引言 在微信小程序开发中,权限管理和用户身份验证是确保数据安全、保护用户隐私以及提供个性化服务的关键环节。本文将深入探讨微信小程序中如何实现权限管理和用户身份验证…...
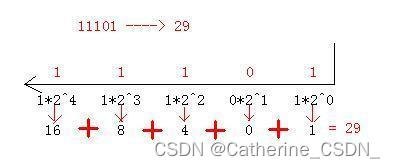
Python3 笔记:二进制的转换
十进制是逢十进一,二进制就是逢二进一。 十进制里最大的数字是9,二进制里最大的数字是1。 11010010001000010000010000001000000010^0110^11010^210010^3100010^41000010^510000010^6100000010^7100000002^012^122^242^382^4162^5322^6642^7128 1、十进…...
代码审计-PHP模型开发篇动态调试反序列化变量覆盖TP框架原生POP链
知识点 1、PHP审计-动态调试-变量覆盖 2、PHP审计-动态调试-原生反序列化 3、PHP审计-动态调试-框架反序列化PHP常见漏洞关键字 SQL注入: select insert update delete mysql_query mysqli等 文件上传: $_FILES,type"file"&…...

前端动态旋转地球背景
效果图 贴下源码 <template><div class"map-bg"><div class"canvas" id"canvs"></div><canvas class"canvasxk" id"canv"></canvas></div> </template><script setup …...
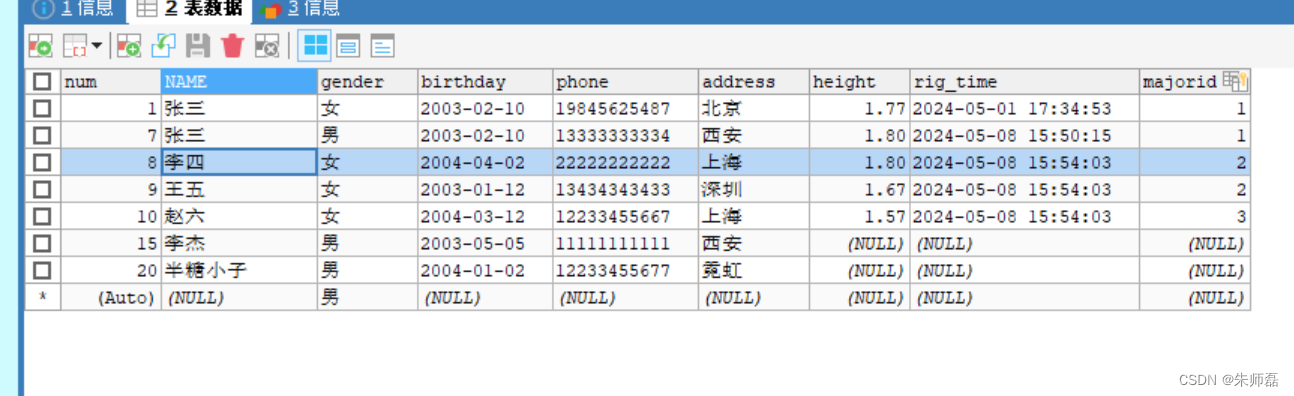
MySQL中的子查询
子查询,在一个查询语句中又出现了查询语句 子查询可以出现在from和where后面 from 表子查询(结果一般为多行多列)把查询结果继续当一张表对待 where 标量子查询(结果集只有一行一列)查询身高最高的学生,查询到一个最高身高 列子查询(结果集只有一行多列) 对上表进行如下操作 …...
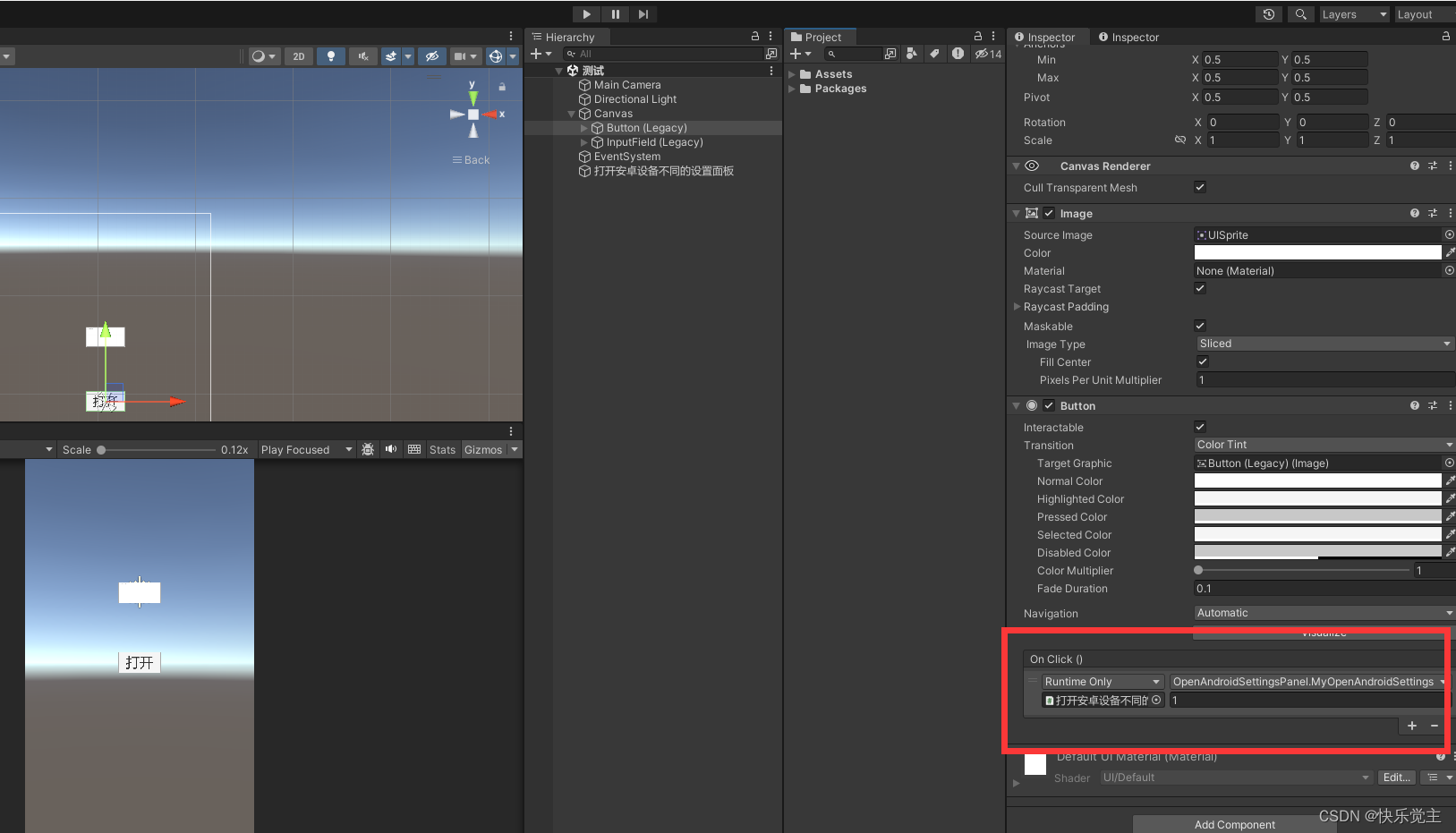
Unity打开安卓设备不同的设置面板
1,打开安卓设备不同的设置面板,我还贴心的把Android官网的链接放下面了 2,使用也很方便:unity按钮事件上拖这个脚本,注册MyOpenAndroidSettings方法,参数 填 和枚举值相应的数字 // 功能:打开…...

低空经济+无人机:低空物资运输技术详解
随着科技的飞速发展和航空产业的日益壮大,低空经济已成为全球经济的重要组成部分。无人机作为低空经济的重要载体,其在低空物资运输领域的应用逐渐凸显,为物流、救援等多个领域带来了革命性的变革。 一、低空经济概述 低空经济是指在垂直高度…...

全场景智能终端RK3288主板在智能垃圾回收项目的应用,支持鸿蒙,支持全国产化
全场景智能终端主板AIoT-3588A推出的智能化垃圾回收项目,旨在解决城市化进程中日益突出的垃圾处理问题。智能垃圾分类箱具备触屏操作、自动称重、分类投放以及电子语音播报提示等多项功能,居民能够经过分类积分卡、手机扫码、人脸识别等多种途径进行投放…...

QT设计模式:建造者模式
基本概念 建造者模式是一种创建型设计模式,它允许你创建复杂对象的过程独立于该对象的组成部分以及它们的组装方式。这样可以构造出不同的对象表示。 在建造者模式中,将创建对象的过程和对象的表示分离,通过一步步的构建,可以得…...
个人微信api
简要描述: 退出群聊 请求URL: http://域名地址/quitChatRoom 请求方式: POST 请求头Headers: Content-Type:application/json Authorization:login接口返回 参数: 参数名 必选 类型 …...

使用Ownips工具获取海外电商网站wish商品价格
一、引言 在数字化浪潮汹涌的今天,互联网已经成为我们生活、工作中不可或缺的一部分。而在这个虚拟的世界里,每一个设备都需要一个独特的标识来确保信息的准确传递,这个标识就是IP地址。而在众多IP地址中,静态IP因其独特的稳定性…...

【FFmpeg】调用ffmpeg进行H264软解
调用FFmpeg库实现264软件解码 1. FFmpeg的编译2. 调用FFmpeg实现H264软解2.1 基本框架2.2 代码实现2.3 测试结果 3. 分析工具3.1 码流分析3.2 YUV分析 示例工程 【FFmpeg】调用FFmpeg库实现264软编 1. FFmpeg的编译 FFmpeg在Windows下的编译参考:http://t.csdni…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
