【算法刨析】完全背包
完全背包与01背包的区别
01背包对于一个物品只能选择一次,但是完全背包可以选择任意次;
思路
和01背包类似,01背包我们只需要判断选或不选,完全背包也是如此,不同的是,对于这个物品我们在判断选后在增加一次选择的机会,直到不选,跳转至下一个物品即可;
一般代码:
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
第k次,不选的话就是它本身,选的话就是直接选择k次即可;
当然这个代码在数据稍微大一点的时候就会超出时间限制;
#include<iostream>
using namespace std;
const int N=1004;
int f[N][N];
int w[N],v[N];int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){for(int k=0;k*v[i]<=j;k++){f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}}}cout<<f[n][m]<<endl;
}优化思路
上面代码会超出时间限制是因为三层循环,下面我们来把第三层循环优化掉:
f[i][j]=max(f[i][j],f[i-1][j-v]+w,f[i-1][j-2*v]+2*w,f[i-1][j-3*v]+3*w......f[i-1][j-k*v]+k*w)
f[i][j-v]=max( f[i][j-v],f[i-1][j-2*v]+w,f[i-1][j-3*v]+2*w......f[i-1][j-k*v]+k*w)
f[i-1][j-v]+w,f[i-1][j-2*v]+2*w,f[i-1][j-3*v]+3*w......f[i-1][j-k*v]+k*w 不就是f[i][j-v]+w
那么我们可以得到:f[i][j]=max(f[i][j],f[i-1][j-v]+w)
这样我们不就可以不用写第三层循环了吗?
直接用:
f[i][j]=f[i-1][j];
if(j>=v[i])
f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
优化代码:
#include<iostream>
using namespace std;
const int N=1004;
int f[N][N];
int w[N],v[N];int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++){cin>>v[i]>>w[i];}for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);}}cout<<f[n][m]<<endl;
}我们来看一下核心代码:
f[i][j]=f[i-1][j];
if(j>=v[i])
f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);还记得01背包的代码吗?
f[i][j] = f[i - 1][j];if(j>=v[i])
f[i][j]= max( f[i - 1][j],f[i - 1][j - v[i]] + w[i] );是不是只有(红色标记):
f[i][j]= max( f[i - 1][j],f[i - 1][j - v[i]] + w[i] );不同
再次优化代码:
注意:
这里我的j的大小是从小到大开始的:
01背包中,f[i][j]= max( f[i - 1][j],f[i - 1][j - v[i]] + w[i] );对于f[j]就相当于f[i-1][j]的大小,如果从小到大遍历,那么f[i-1][j]的大小就会发现变化,那么优化后的代码就不满足我们所推导的公式,所以我们要从大到小;
类比于01背包,完全背包的公式, f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);对于这个公式如果从大到小就会改变f[i][j]的大小,不满足所推导的公式;
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e4;
int f[N];
int w[N],v[N];int main()
{int n,m;cin>>n>>m;for(int i=0;i<n;i++)cin>>v[i]>>w[i];for(int i=0;i<n;i++){for(int j=v[i];j<=m;j++){f[j]=max(f[j],f[j-v[i]]+w[i]);}}cout<<f[m]<<endl;
}以上就是全部内容!!
相关文章:

【算法刨析】完全背包
完全背包与01背包的区别 01背包对于一个物品只能选择一次,但是完全背包可以选择任意次; 思路 和01背包类似,01背包我们只需要判断选或不选,完全背包也是如此,不同的是,对于这个物品我们在判断选后在增加一…...
notepad++
文章目录 换行 换行 根据需要选择是否要自动换行或者一行展示。 点击视图 选中或者取消选中自动换行...
Python ValueError: bad transparency mask
修改前 修复后 运行正常 from PIL import Image# 读取图片 #报错信息解决ValueError: bad transparency mask--相关文档地址https://blog.csdn.net/kalath_aiur/article/details/103945309 #1. 检查 alpha 通道是否是一个有效的掩码。如果不是,则需要对 alpha 通道…...

Linux本地部署Nightingale夜莺监控并实现远程访问提高运维效率
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
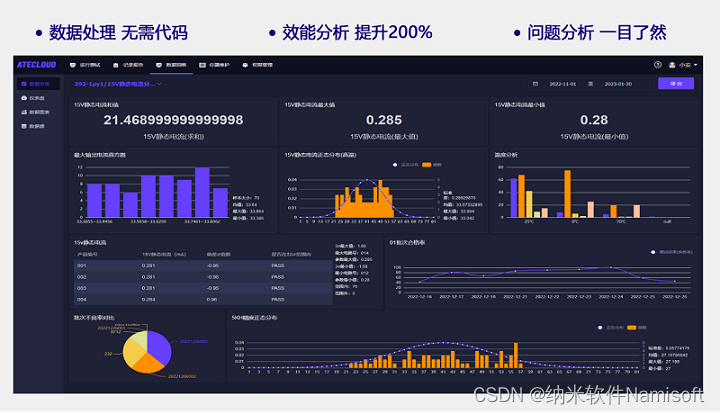
开关电源功率测试方法:输入、输出功率测试步骤
在现代电子设备中,开关电源扮演着至关重要的角色,其效率和稳定性直接影响到整个系统的性能。因此,对开关电源进行功率测试成为了电源管理的重要环节。本文将详细介绍如何使用DC-DC电源模块测试系统对开关电源的输入输出功率进行准确测量&…...

QT 文字转语言插件
1.在工程.pro文件中添加 QT texttospeech 2.在头文件中添加 #include <QTextToSpeech> 3.使用的方法 QString str"欢迎使用智慧教育学习平台";QTextToSpeech *Speechernew QTextToSpeech;const QVector<QVoice> voices Speecher->availableV…...
的认证(Authentication)策略解析)
Kubernetes(k8s)的认证(Authentication)策略解析
Kubernetes(k8s)的认证(Authentication)策略是确保只有经过验证的实体(用户、服务账户等)能够访问API服务器的基础安全措施。Kubernetes支持多种认证方法,以下是主要的认证策略: X50…...

Scikit-Learn决策树
Scikit-Learn决策树 1、决策树分类2、Scikit-Learn决策树分类2.1、Scikit-Learn决策树API2.2、Scikit-Learn决策树初体验2.3、Scikit-Learn决策树实践(葡萄酒分类) 1、决策树分类 2、Scikit-Learn决策树分类 2.1、Scikit-Learn决策树API 官方文档&#…...

Python面试题【python基础部分1-50】
Python面试题【python基础部分1-50】 Python面试题【python基础部分1-50】 Python面试题【python基础部分1-50】 问题:如何在Python中交换两个变量的值? 答案: a, b b, a问题:Python中的列表和元组有什么区别? 答案&…...

鸿蒙内核源码分析(Shell编辑篇) | 两个任务,三个阶段
系列篇从内核视角用一句话概括shell的底层实现为:两个任务,三个阶段。其本质是独立进程,因而划到进程管理模块。每次创建shell进程都会再创建两个任务。 客户端任务(ShellEntry): 负责接受来自终端(控制台)敲入的一个个字符&…...

第Ⅷ章-Ⅱ 组合式API使用
第Ⅷ章-Ⅱ 组合式API使用 provide与inject的使用vue 生命周期的用法编程式路由的使用vuex的使用获取DOM的使用setup语法糖setup语法糖的基本结构响应数据的使用其它语法的使用引入组件的使用 父组件传值的使用defineProps 父传子defineEmits 子传父 provide与inject的使用 pro…...
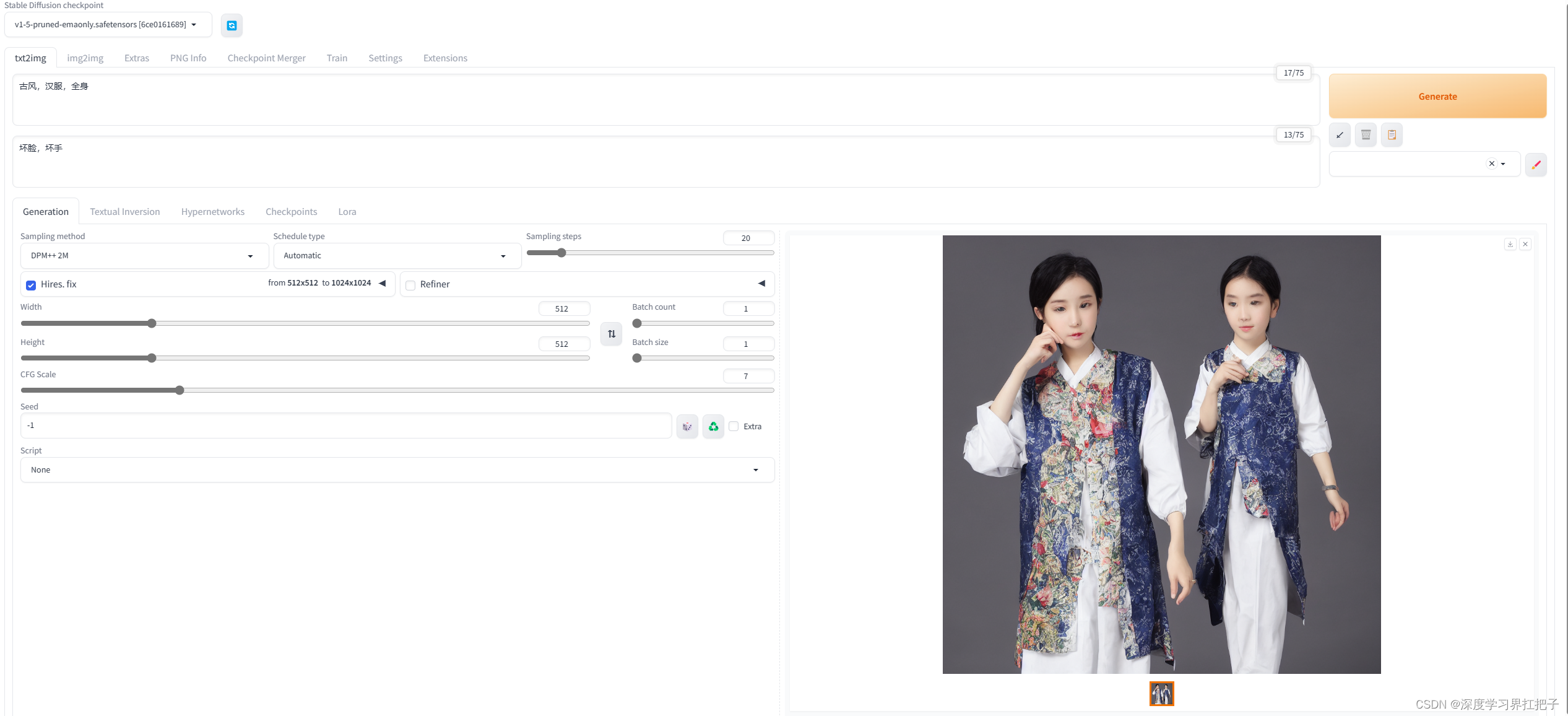
stable-diffusion-webui配置
源码地址 https://github.com/AUTOMATIC1111/stable-diffusion-webui.git报错Fresh install fail to load AttributeError: NoneType object has no attribute _id pydantic降级 pip uninstall pydantic pip install pydantic1.10.11记得要把clip-vit-large-patch14放在opena…...
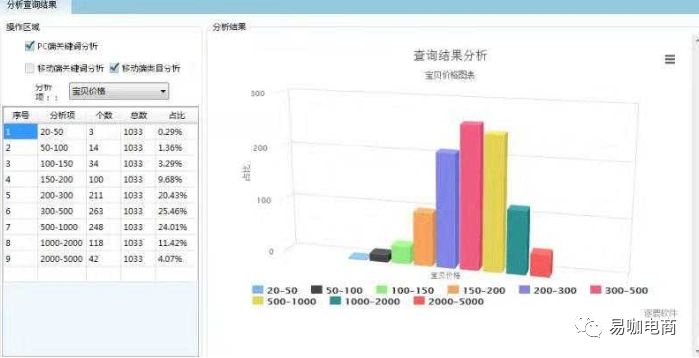
1+X电子商务数据采集渠道及工具选择(二)||电商数据采集API接口
电商数据采集API 接口 ◆适用范围 淘宝:可以采集到所属淘宝、天猫店铺的流量、销售、产品、运营相关数据;需要采集行业市场数据,则需要选择市场行情版。 京东:采集京东等其他平台店铺数据 jd.item_get 公共参数 名称类型必须描述keyString是调用key&…...
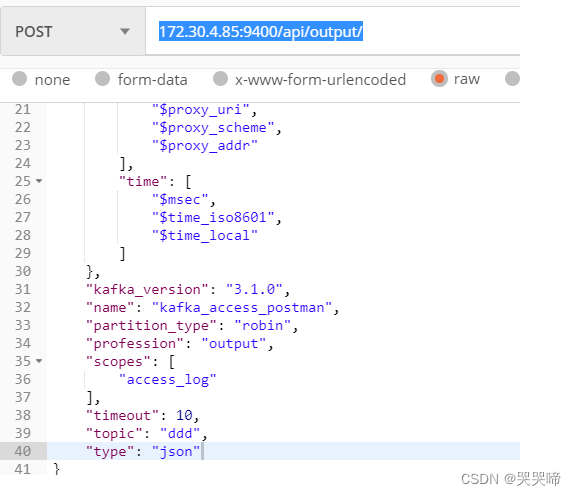
apinto OpenAPI
OpenApi 上游 查询列表 查询详情 新增 { "name": "jg_upstream", "driver": "http", "description": "通过postman添加上游", "scheme": "HTTPS", "retry":"1", "…...
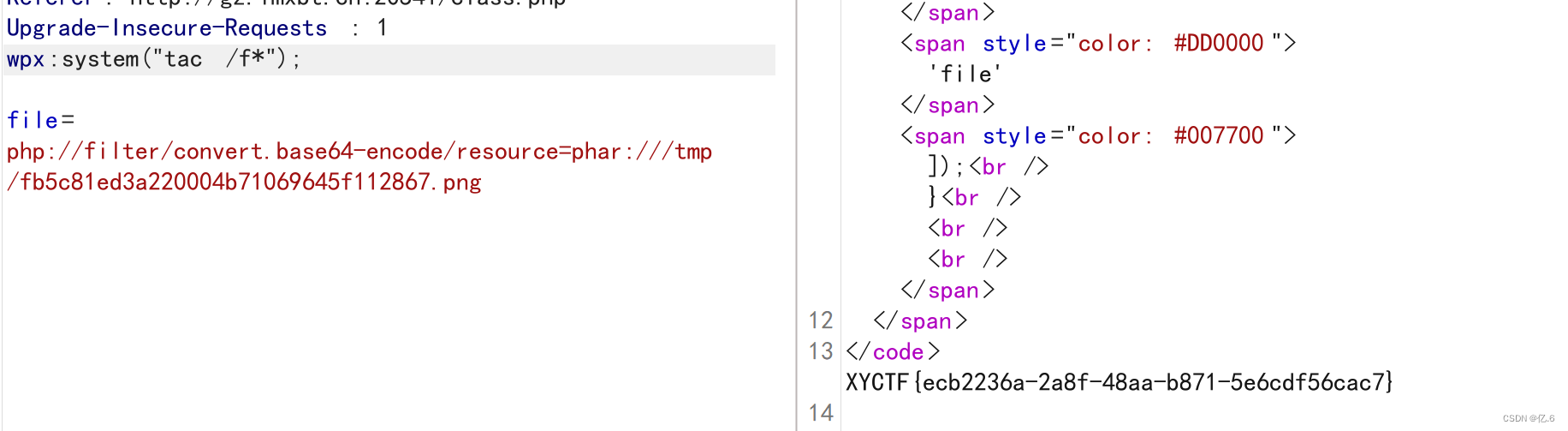
XYCTF - web
目录 warm up ezMake ezhttp ezmd5 牢牢记住,逝者为大 ezPOP 我是一个复读机 ezSerialize 第一关 第二关 第三关 第一种方法: 第二种方法: ez?Make 方法一:利用反弹shell 方法二:通过进制编码绕过 ε…...
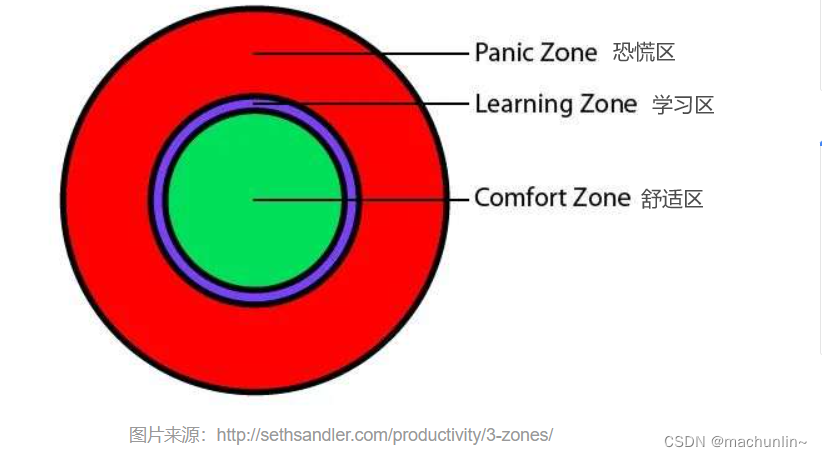
学习方法的重要性
原贴:https://www.cnblogs.com/feily/p/13999204.html 原贴:https://36kr.com/p/1236733055209095 1、 “一万小时定律”的正确和误区 正确: 天才和大师的非凡,不是真的天资超人一等,而是付出了持续不断的努力&…...

把现有的 Jenkins 容器推送到一个新的镜像标签,并且重新启动新的容器
要把现有的 Jenkins 容器推送到一个新的镜像标签,并且重新启动新的容器,你可以按照以下步骤操作: 停止当前正在运行的 Jenkins 容器(如果你不想在操作时中断服务,可以跳过此步骤,直接进行下一步)…...

难以重现的 Bug如何处理
对很多测试人员(尤其是对新手来说)在工作过程中最不愿遇到的一件事情就是:在测试过 程中发现了一个问题,觉得是 bug,再试的时候又正常了。 碰到这样的事情,职业素养和测试人员长期养成的死磕的习性会让她…...

我与足球的故事 | 10年的热爱 | 伤病 | 悔恨 | 放弃 or 继续 | 小学生的碎碎念罢了
今天不分享技术博客,今天不知道为什么就是想写我和足球的故事(手术完两个礼拜,手还是很疼那个,就连打字都费劲),上面两张图是我最喜欢的两个球星,当然因为之前特别喜欢巴萨,也特别喜…...

js图片回显的方法
直接上代码: <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body>// HTML部分<input type"file" id"fileInput"><button onclick"show…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
