呼叫中心系统选pscc好还是okcc好
选择PSCC(商业软件呼叫中心)还是OKCC(开源呼叫中心),应基于以下几个关键因素来决定:
-
技术能力:如果企业拥有或愿意投入资源培养内部技术团队,开源解决方案可能更合适,因为它允许高度定制化并可以深入了解和控制代码。
-
预算:开源呼叫中心系统通常具有较低的初始成本,但可能需要投入更多的时间和人力来维护和升级。商业解决方案虽然初期投资较高,但通常包括全面的技术支持和服务。
-
定制化需求:如果企业需要特定的功能或对系统有特别的定制需求,开源系统提供了更大的灵活性。商业系统虽然也提供定制服务,但可能受限于提供商的定制能力和政策。
-
服务和支持:商业呼叫中心系统通常提供专业的客户支持和服务保障,这对于没有足够技术支持能力的企业来说非常重要。开源系统依赖社区支持,可能在响应时间和专业程度上有所不足。
-
安全性和合规性:商业解决方案通常提供经过验证的安全特性和符合行业标准的合规性,这对于处理敏感数据的呼叫中心尤为重要。开源系统虽然也可以实现高安全标准,但需要企业自行确保。
-
系统稳定性和可靠性:商业系统往往经过严格测试,提供更高的稳定性和可靠性。开源系统虽然也很稳定,但可能存在依赖特定开发者贡献的风险。
-
实施和培训:商业系统通常提供易于理解的用户界面和培训资源,有助于快速部署和使用。开源系统可能需要更多的时间来学习和适应。
综上所述,没有绝对的“好”或“坏”,而是哪一种类型的系统更适合特定企业的需求。建议企业根据自身情况综合考虑以上因素,进行细致评估后做出选择,欢迎和博主一起技术交流。
相关文章:

呼叫中心系统选pscc好还是okcc好
选择PSCC(商业软件呼叫中心)还是OKCC(开源呼叫中心),应基于以下几个关键因素来决定: 技术能力:如果企业拥有或愿意投入资源培养内部技术团队,开源解决方案可能更合适,因为…...

【SRC实战】前端脱敏信息泄露
挖个洞先 https://mp.weixin.qq.com/s/xnCQQCAneT21vYH8Q3OCpw “ 以下漏洞均为实验靶场,如有雷同,纯属巧合 ” 01 — 漏洞证明 一、前端脱敏,请求包泄露明文 “ 前端脱敏处理,请求包是否存在泄露? ” 1、获取验…...
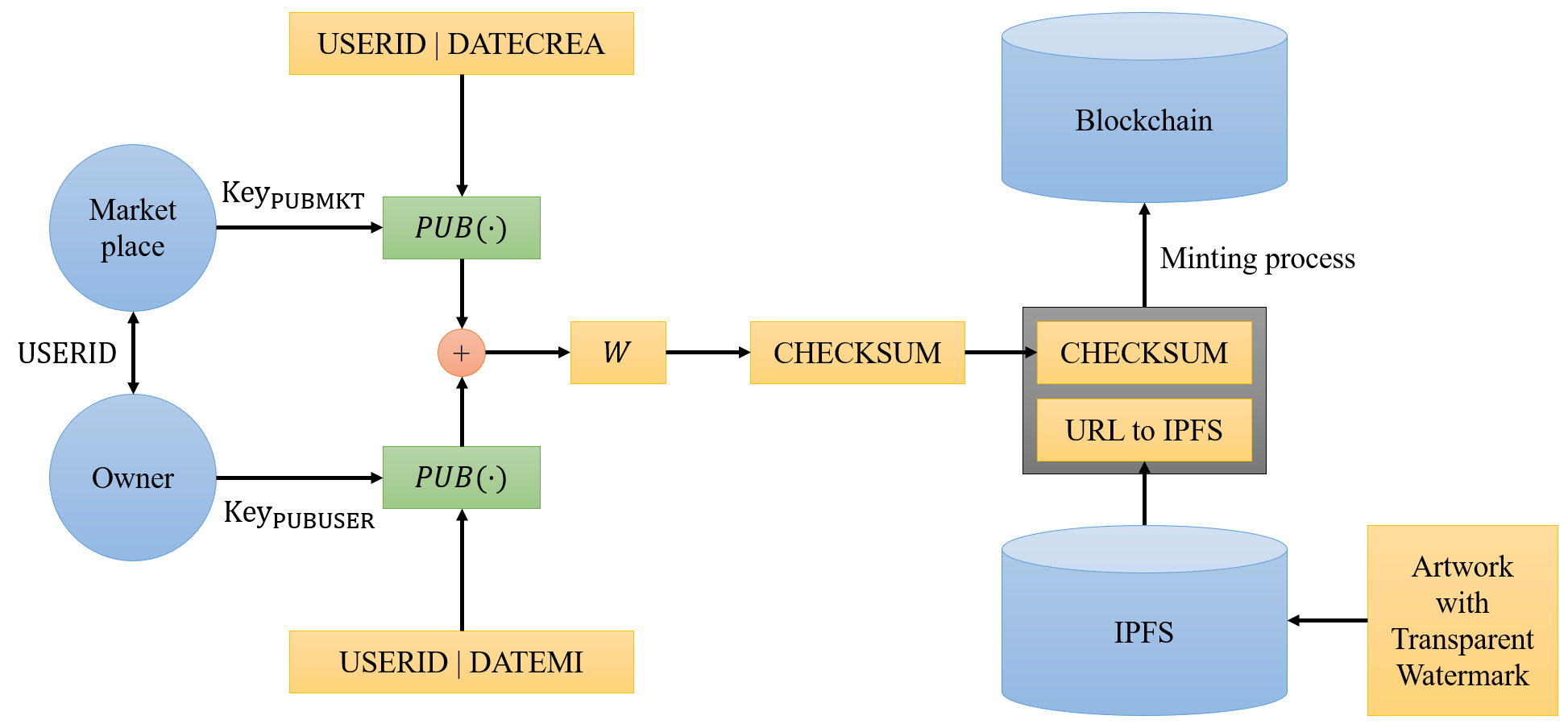
区块链 | NFT 水印:Review on Watermarking Techniques(三)
🍍原文:Review on Watermarking Techniques Aiming Authentication of Digital Image Artistic Works Minted as NFTs into Blockchains 一个 NFT 的水印认证协议 可以引入第三方实体来实现对交易的认证,即通过使用 R S A \mathsf{RSA} RSA…...

初识C语言——第十九天
for循环 1.简单概述 2.执行流程 3.建议事项:...

软件需求工程习题
1.(面谈)是需求获取活动中发生的需求工程师和用户间面对面的会见。 2.使用原型法进行需求获取,(演化式)原型必须具有健壮性,代码质量要从一开始就能达到最终系统的要求 3.利用面谈进行需求获取时…...

Win10弹出这个:https://logincdn.msauth.ne
问题描述: Win10脚本错误 Windows10家庭版操作系统开机后弹出这个 https://logincdn.msauth.net/shared/1.0/content/js/ConvergedLogin_PCore_vi321_9jVworKN8EONYo0A2.js 解决方法: 重启计算机后手动关闭第三方安全优化软件,然后在任务管理…...

Vue2 动态路由
VUE CLI 项目 router.js import Vue from "vue"; import Router from "vue-router"; import base from "/view/404/404.vue";const originalPush Router.prototype.push Router.prototype.push function push (location) {return originalPu…...

LeetCode746:使用最小花费爬楼梯
题目描述 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你计算并返回达到楼梯顶部的最低花费。 代码 …...

DockerFile介绍与使用
一、DockerFile介绍 大家好,今天给大家分享一下关于 DockerFile 的介绍与使用,DockerFile 是一个用于定义如何构建 Docker 镜像的文本文件,具体来说,具有以下重要作用: 标准化构建:提供了一种统一、可重复…...
 字符串)
Java基础知识(六) 字符串
六 字符串 6.1 String字符串 1、String类对象创建 定义String类对象格式:** 1)String 字符串变量名“字符串常量”; 2)String 字符串变量名new String(字符串常量); 3)String 字符串变量名; 字符串变量名“字符串常…...

为什么跨境电商大佬都在自养号测评?看完你就懂了!
在跨境电商的激烈竞争中,各大平台如亚马逊、拼多多Temu、shopee、Lazada、wish、速卖通、煤炉、敦煌、独立站、雅虎、eBay、TikTok、Newegg、Allegro、乐天、美客多、阿里国际、沃尔玛、Nike、OZON、Target以及Joom等,纷纷成为商家们竞相角逐市场份额的焦…...

AtCoder Beginner Contest 353
A 题意:检查是否有比第一个数大的数 #include<bits/stdc.h>using namespace std;int main() {int n;cin>>n;int a;cin>>a;int f0;for(int i2;i<n;i){int k;cin>>k;if(k>a){cout<<i<<endl;f1;break;}}if(f0){cout<&l…...

深度解读《深度探索C++对象模型》之虚继承的实现分析和效率评测(一)
目录 前言 具有虚基类的对象的构造过程 通过子类的对象存取虚基类成员的实现分析 接下来我将持续更新“深度解读《深度探索C对象模型》”系列,敬请期待,欢迎左下角点击关注!也可以关注公众号:iShare爱分享,或文章末…...

计算机Java项目|Springboot房产销售系统
作者主页:编程指南针 作者简介:Java领域优质创作者、CSDN博客专家 、CSDN内容合伙人、掘金特邀作者、阿里云博客专家、51CTO特邀作者、多年架构师设计经验、腾讯课堂常驻讲师 主要内容:Java项目、Python项目、前端项目、人工智能与大数据、简…...
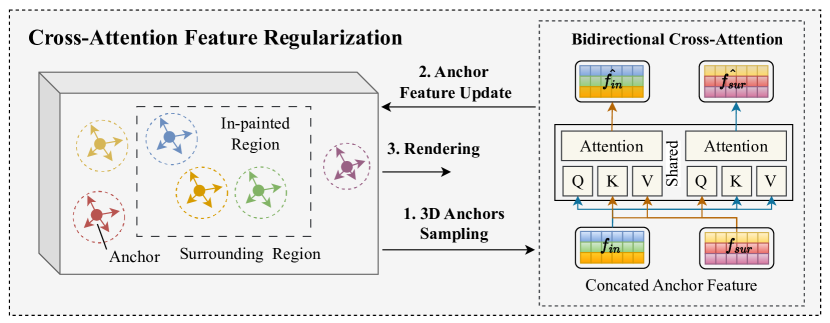
学习3D几何和特征一致的高斯溅射目标去除
earning 3D Geometry and Feature Consistent Gaussian Splatting for Object Removal 学习3D几何和特征一致的高斯溅射目标去除 Yuxin Wang 王玉欣 HKUST &Qianyi Wu Monash University &Guofeng Zhang Zhejiang University &Dan Xu HKUST 香港科技大学&吴倩…...

PHP 使用常量实现枚举类
PHP 使用常量实现枚举类 <?php abstract class Enum {private static $constCacheArray NULL;private static function getConstants() {if (self::$constCacheArray NULL) {self::$constCacheArray [];}$calledClass get_called_class();if (!array_key_exists($call…...

Linux操作系统基础题库
一. 单选题(共2题,40分) 1. (单选题)Linux操作系统自诞生至今,有数十万的程序开发人员参与到了它的开发与完善中,如今Linux已发展成为是一个成熟、稳定的操作系统。从以下选项中选出关于Linux特点描述完全正确的一项。…...

Java抽象类:为何它是你代码架构的基石?
目录 1、抽象类的概念 2、抽象类语法 3、抽象类特性 4、抽象类的作用 5、 完结散花 个人主页:秋风起,再归来~ 文章专栏:javaSE的修炼之路 个人格言:悟已往之不谏,知来者犹可追 克…...

Flutter 中的 ToggleButtons 小部件:全面指南
Flutter 中的 ToggleButtons 小部件:全面指南 在 Flutter 中,ToggleButtons 是一种允许用户在一组选项中进行切换选择的控件。它通常用于展示一组相关选项,让用户可以快速切换选择。ToggleButtons 是一种水平排列的按钮集合,其中…...
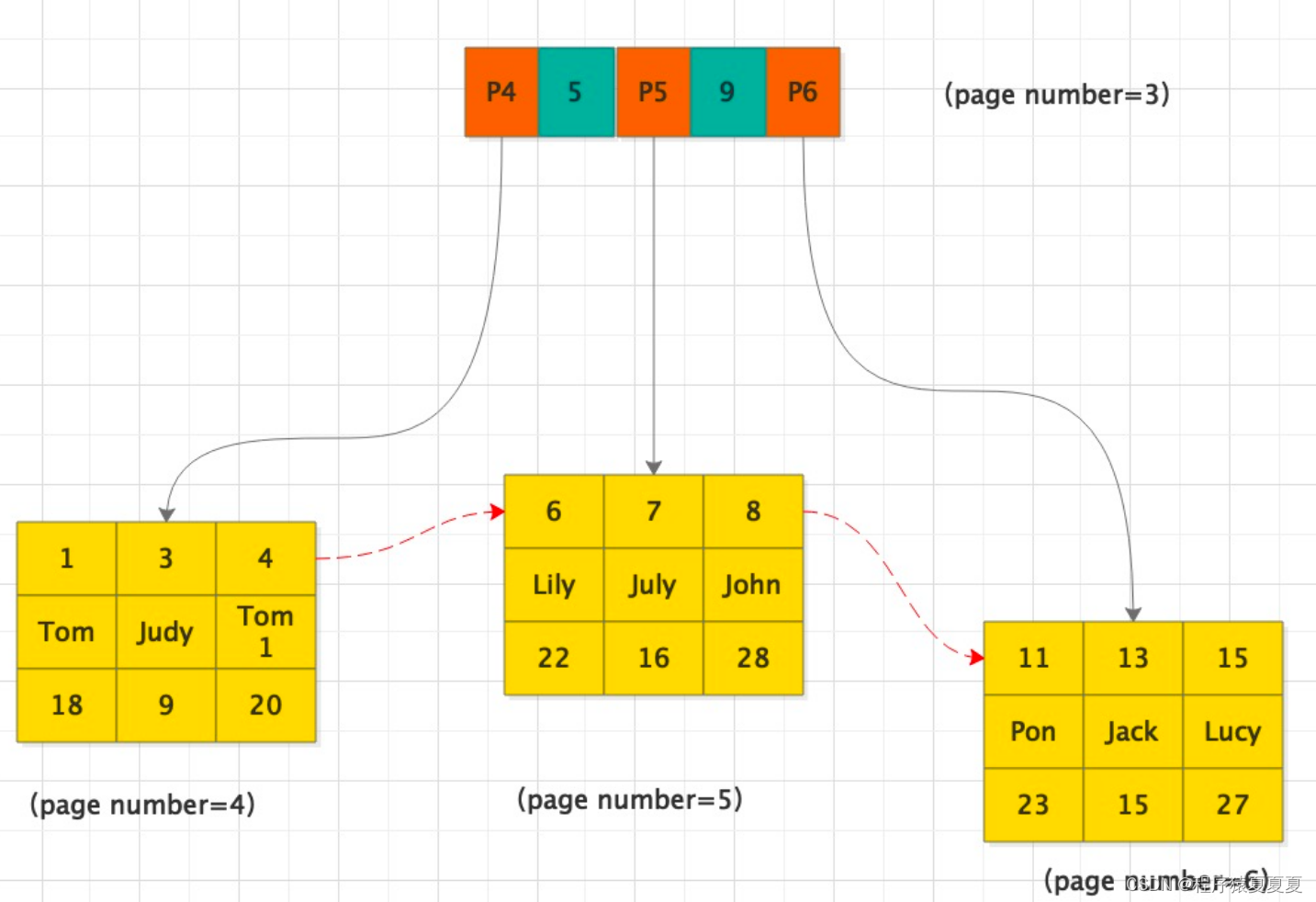
【MYSQL】一颗B+树可以保存多少条数据
引言 事万物都有自己的单元体系,若干个小单体组成一个个大的个体。就像拼乐高一样,可以自由组合。所以说,如果能熟悉最小单元,就意味着我们抓住了事物的本事,再复杂的问题也会迎刃而解。 存储单元 存储器范围比较大…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
