Day53代码随想录动态规划part13:300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
Day52 动态规划part13
300.最长递增子序列
leetcode链接:300. 最长递增子序列 - 力扣(LeetCode)
题意:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
- 输入:nums = [10,9,2,5,3,7,101,18]
- 输出:4
- 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
思路:
- dp数组定义:dp[i]是以nums[i]为结尾的最长递增子序列长度
- 状态转移方程:位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
- dp[i]的初始化:每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1
- 遍历顺序:两层循环。dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
- 推导
- 扩展:也可以用贪心做!
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:dp = [1] * len(nums)for i in range(1, len(nums)):for j in range(0, i):if nums[j] < nums[i]: dp[i] = max(dp[i], dp[j]+1)print(dp)return max(dp)
674. 最长连续递增序列
leetcode链接:. - 力扣(LeetCode)
题意:相比于上一题,这题是连续的
思路:只用和i-1比较了,都不用有循环了
class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:dp = [1]*len(nums)for i in range(1, len(nums)):if nums[i-1] < nums[i]:dp[i] = max(dp[i], dp[i-1]+1)return max(dp)
718. 最长重复子数组
leetcode链接:718. 最长重复子数组 - 力扣(LeetCode)
题意:给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:长度最长的公共子数组是 [3, 2, 1] 。
思路:用二维数组可以记录两个字符串的所有比较情况
- 确定dp数组(dp table)以及下标的含义:dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
- 递推公式:dp[i][j] = dp[i-1][j-1]+1
- 初始化:根据dp[i][j]的定义,dp[i][0] 和dp[0][j]其实都是没有意义的!但dp[i][0] 和dp[0][j]要初始值,因为 为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;所以dp[i][0] 和dp[0][j]初始化为0。举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来。
- 遍历顺序:外层for循环遍历A,内层for循环遍历B。其实先遍历B也可以的
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:lena = len(nums1)lenb = len(nums2)dp = [[0]*(lenb+1) for i in range(lena+1)] #注意b是行!a是列!result = 0for i in range(1, lena+1):for j in range(1, lenb+1):# print(i,j,nums1[i-1],nums2[j-1])if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1if dp[i][j]>result:result = dp[i][j]# result = max(result, max(dp[i]))# print(dp)return result
相关文章:

Day53代码随想录动态规划part13:300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
Day52 动态规划part13 300.最长递增子序列 leetcode链接:300. 最长递增子序列 - 力扣(LeetCode) 题意:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除&a…...

自己动手为wordpress注册一个Carousel轮播区块
要为WordPress注册一个Carousel轮播区块,你可以创建一个自定义Gutenberg块。以下是一个简单的示例,说明如何创建一个Carousel轮播区块: 1. 在你的主题目录中创建一个名为carousel-block的子文件夹。在这个文件夹中,创建一个名为c…...

基于Springboot的实习生管理系统(有报告)。Javaee项目,springboot项目。
演示视频: 基于Springboot的实习生管理系统(有报告)。Javaee项目,springboot项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&a…...
良心实用的电脑桌面便利贴,好用的便利贴便签小工具
在日常办公中,上班族经常需要记录临时任务、重要提醒或者突发的灵感。比如,在紧张的项目会议中,忽然想到一个改进的点子,或者是在处理邮件时,需要记下对某个客户的回复要点。在这些场景下,如果能直接在电脑…...
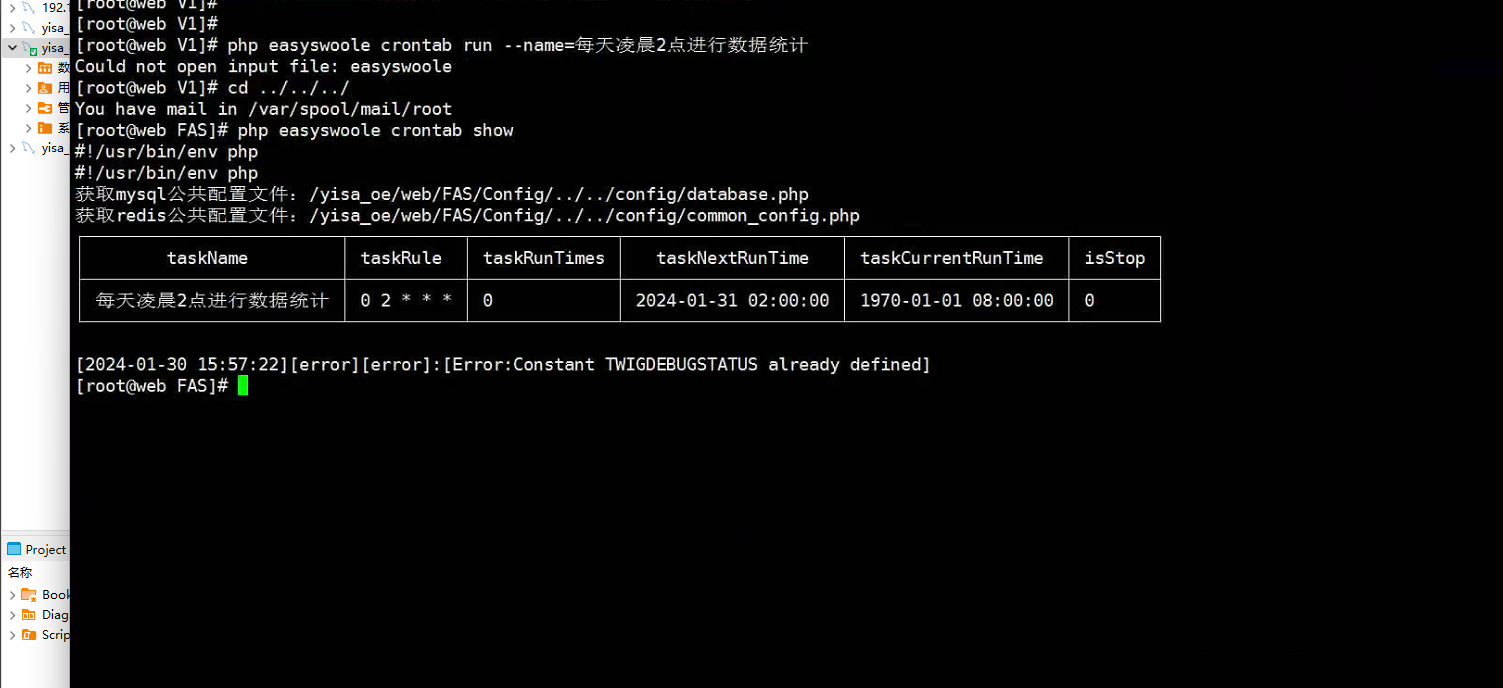
Eayswoole 报错 crontab info is abnormal
在执行一个指定的定时任务时 如 php easyswoole crontab show 报错 crontab info is abnormal 如下图所示: 查询了半天 修改了如下配置: 旧的 // 创建定时任务实例 $crontab new \EasySwoole\Crontab\Crontab($crontabConfig); 修改后&#…...

移动 App 入侵与逆向破解技术-iOS 篇
如果您有耐心看完这篇文章,您将懂得如何着手进行app的分析、追踪、注入等实用的破解技术,另外,通过“入侵”,将帮助您理解如何规避常见的安全漏洞,文章大纲: 简单介绍ios二进制文件结构与入侵的原理介绍入…...

2024服贸会,参展企业媒体宣传报道攻略
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 2024年中国国际服务贸易交易会(简称“服贸会”)是一个重要的国际贸易平台,对于参展企业来说,有效的媒体宣传报道对于提升品牌知名度、扩大…...
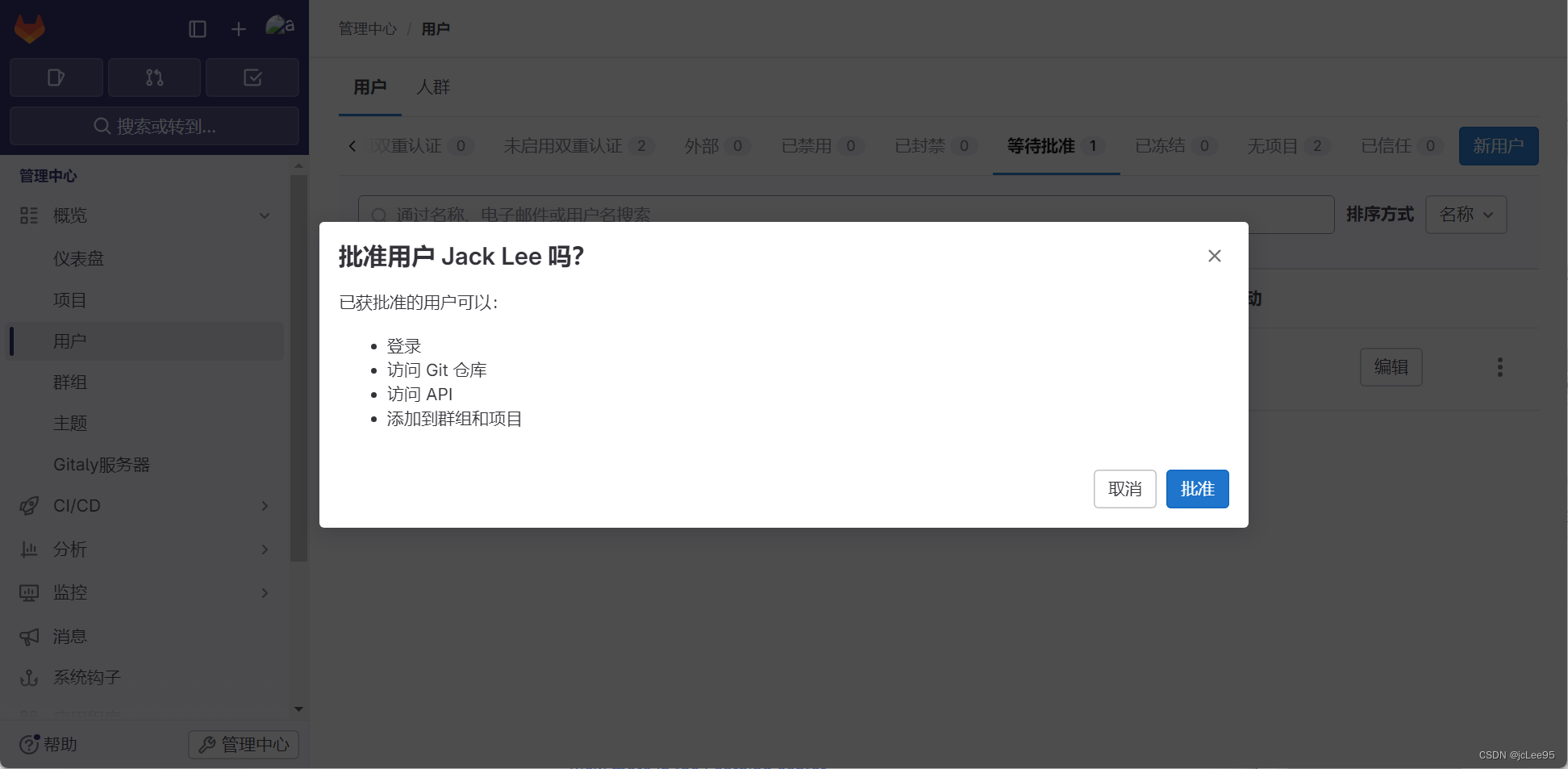
CI/CD笔记.Gitlab系列.新用户管理
CI/CD笔记.Gitlab系列 新用户管理 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://blog.csdn.net/qq_285502…...

前端 JS 经典:JS 基础类型和 typeof
前言:JS 基础类型就 8 种,这是官方确定的,毋庸置疑。其中原始类型 7 种,对象类型 1 种。而 typeof 关键字是用来判断数据是属于什么类型的。 1. 原始类型 Number、Boolean、String、BigInt、symbol、Undefined、null typeof 18…...
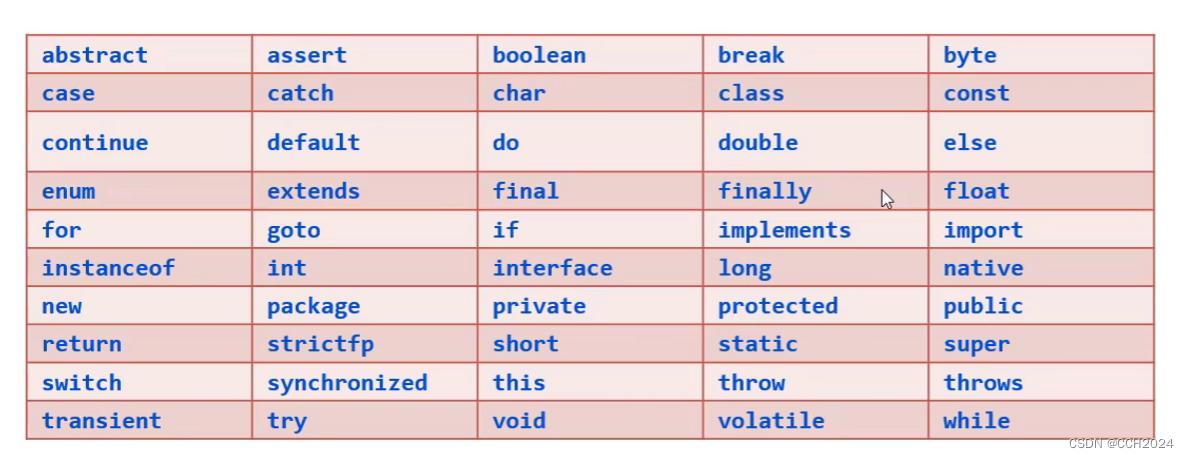
Java入门基础学习笔记11——关键字和标识符
1、关键字 关键字是java中已经被赋予特定意义的,有特殊作用的一些单词,不可以把这些单词作为标识符来使用。 注意:关键字是java用了的,我们就不能用来作为:类名、变量名、否则会报错。 标识符: 标识符就是…...

设计模式-解释器模式(Interpreter)
1. 概念 解释器模式(Interpreter Pattern)是一种行为型设计模式,它用于定义一个语言的文法,并解析语言中的表达式。具体来说,解释器模式通过定义一个解释器来解释语言中的表达式,从而实现对语言的解析和执…...
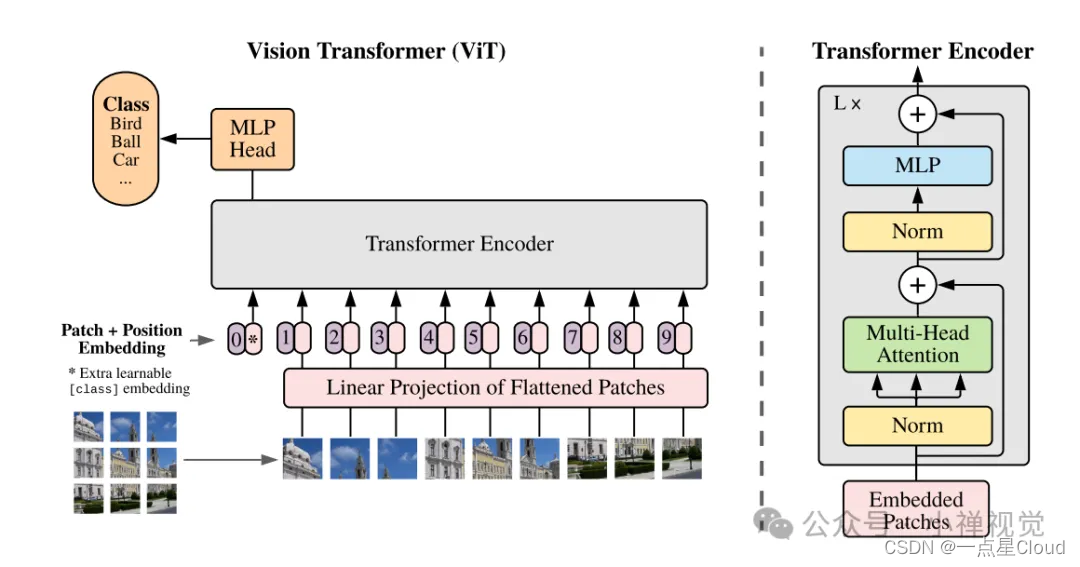
机器视觉任务中语义分割方法的进化历史
机器视觉任务中语义分割方法的进化历史 一、基于传统方法的图像分割二、基于卷积神经网络的图像分割三、基于Attention机制的图像分割四、语义分割模型的挑战与改进 在图像处理领域,传统图像分割技术扮演着重要角色。 一、基于传统方法的图像分割 这些方法包括大津…...
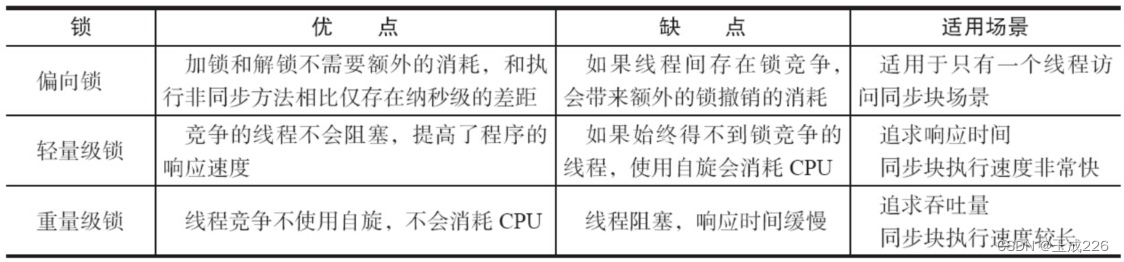
Java并发编程: Synchronized锁升级
文章目录 一、jdk8 markword实现表二、使用工具来查看锁升级三、默认synchronized(o) 一、jdk8 markword实现表 为什么有自旋锁还需要重量级锁: 自旋消耗CPU资源,如果锁的时间长,或者自旋线程多,CPU会被大量消耗。重量…...

Atcoder C - Routing
https://atcoder.jp/contests/arc177/tasks/arc177_c 思路:该问题可以归约为最短路问题,问题中的条件1和条件2是相互独立的,可以分开考虑,从地图中的一个点,沿上下左右四个方向走,所花费的代价为࿱…...

升级! 测试萌新Python学习之连通数据库Pymsql增删改及封装(四)
pymysql 数据库概述python对数据库的增删改查pymysql核心操作事务事务操作pymysql工具类封装每日复习ChatGPT的回答 数据库概述 分类 关系型数据库: 安全 如, mysql oracle SQLite…database tables 行列 非关系型数据库: 高效 如, redis mongoDB…数据存储结构多样 键值对…...

【大数据】containered学习笔记
文章目录 1. Containerd安装1.1 YUM方式安装 【后端&网络&大数据&数据库目录贴】 1. Containerd安装 1.1 YUM方式安装 获取YUM源 获取阿里云YUM源 wget -O /etc/yum.repos.d/docker-ce.repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo 查…...

「TypeScript」TypeScript入门练手题
前言 TypeScript 越来越火,现在很多前端团队都使用它,因此咱们前端码农要想胜任以后的前端工作,就要更加熟悉它。 入门练手题 interface A {x: number;y: number; }type T Partial<A>;const a: T { x: 0, y: 0 }; const b: T { …...

k8s 使用Docker和Containerd对比分析
目录 k8s 使用Docker和Containerd对比分析 互动1:docker build构建的镜像和containerd镜像通用吗? 互动2:k8s1.24之前版本和1.24及1.24之后版本区别? k8s 使用Docker和Containerd对比分析 如果你使用Docker作为K8S容器运行时的…...

MySQL 通过 systemd 启动时 hang 住了……
mysqld:哥,我起不来了…… 作者:贲绍华,爱可生研发中心工程师,负责项目的需求与维护工作。其他身份:柯基铲屎官。 爱可生开源社区出品,原创内容未经授权不得随意使用,转载请联系小编…...

pat乙1033-旧键盘打字
1测试点2: 输入的字符串如果为空,要用getline(cin,s),而不是cin>>s,否则程序做不了 2题目说的如果上键坏了那大写字母打印不了,不是大写转小写打印啦,认真读题 3两个for循环长这样,break…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
