【面试经典题】环形链表

个人主页:一代…
个人专栏:数据结构

在面试中我们经常会遇到有关链表的相关题目,面试官通常会对题目给出拓展
下面我就两个leetcode上的一个双指针的题目为例,并对其进行拓展
题目链接:环形链表
题目描述: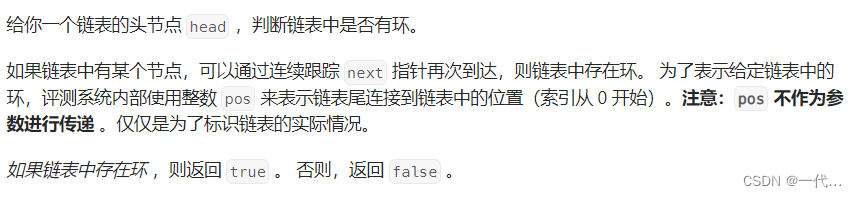
示例: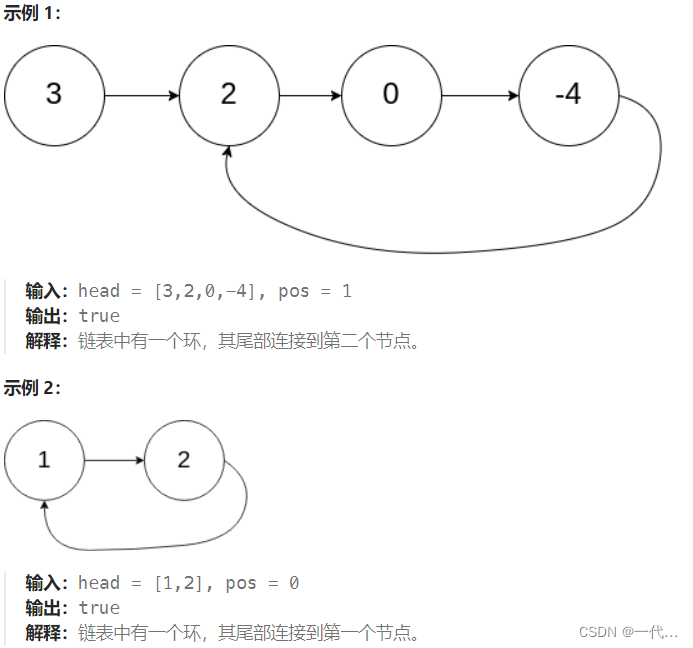
| 思路:运用快慢指针,快指针一次走两步,慢指针一次走一步,若链表带环,则快慢指针一定会在环中相遇,若不带环,则快指针就会走到末尾(NULL或最后一个节点) |
|---|
代码示例:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {ListNode* slow=head;ListNode* fast=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(fast==slow)return true;}return false;
}
|
| 这里while循环中的fast&&fast->next不能调换顺序,因为当链表不带环,节点个数为偶数时,快指针会走到链表为空的位置,当fast->next在前,对空指针进行解引用,就会造成内存访问错误 |
|---|
| (注:fast&&fast->next中如果前一个为假,那么整个表达式为假,就不会对下一个表达式进行计算) |
|---|
拓展面试题目
在带环链表中,当slow每次走一步,fast每次走三步,那么slow会相遇吗?
slow每次走一步,fast每次走三步,那么当slow进环时,fast和slow相距的距离为N,那么没走一次,相距的距离就会减小2.
当链表长度为C时
于是就分为下面两种情况
总结:
1 当N为偶数时,slow和fast在第一轮就会相遇
2 当N为奇数时
C-1为偶数时就会在第二轮相遇
C-1为奇数时一定不会相遇(注:这种结论时错误的,这里下面会讲到)
为什么N是偶数,C时奇数这个条件一定不会成立呢?
假设:链表环之前长度为L,slow和fast相距的距离为N,slow进环时,fast已经在环中转了X圈
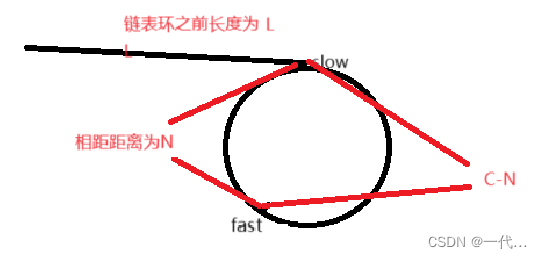
那么就会得出以下几个数学算式:
slow进环时,fast在环中转了X圈,于是fast走过的长度就为L+XC+C-N=L+(X+1)C-N,
slow走过的长度为L
又因为fast走过的长度为slow走过的长度的三倍,所以3L=L+(X+1)C-N
得出2L=(X+1)C-N
2L一定为偶数,当C为偶数,N为奇数时,由算式可得偶数=偶数-奇数,这显然时不出立的,于是就可得出把上面结论中当N为奇数,C-1为奇数时一定不可以追上的结论推翻,于是可证明当在环形链表中fast走3步,slow走1步时,fast和slow一定可以相遇,永远追不上的条件不成立
结论:
1 当N为偶数时,slow和fast在第一轮就会相遇
2 当N为奇数时,C-1为偶数时第一轮追不上,在第二轮就可以追上
题目链接:环形链表II
题目描述:
题目示例: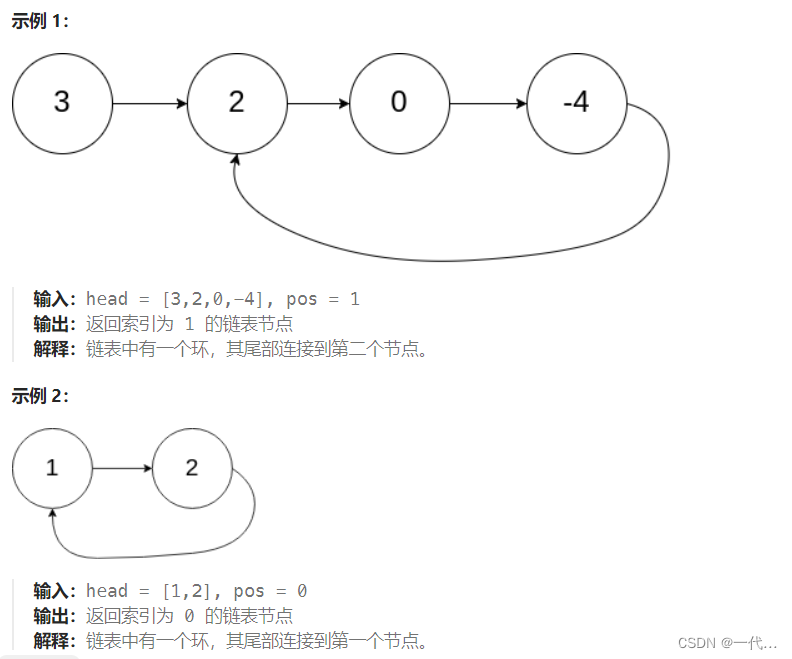
代码示例:
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {ListNode *slow=head,*fast=head;while(fast&&fast->next){fast=fast->next->next;slow=slow->next;if(fast==slow)//相遇{ListNode *meet=slow;while(head!=meet)//相遇的节点即为入环的第一份节点{head=head->next;meet=meet->next;}return meet;}}return NULL;//无环
}
题目思路:定义一个快指针,一个慢指针,快指针一次走一步,慢指针一次走了两步,当两个指针相遇时节点为meet,在让头节点head从头开始走,一次走一步,meet从相遇的地点开始走,一次走一步,当两者相遇时即为入环的第一个节点
那么这是怎么得出来的呢?
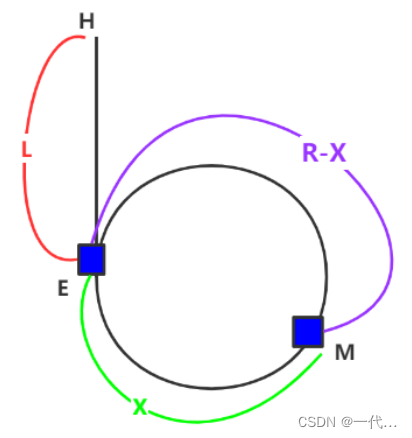
其中E为环的入口点,M为快慢指针的相遇点,L为环之前的链表的长度
由于从slow进环时在到与fast相遇,fast一定不会运动一个环的长度就可以追上slow
假设在slow到环入口时,fast已经转了N圈,环的长度为R
slow运动的距离为L+X
fast运动的距离为L+XR+X
L+NR+X=2L+2X
L=NR-X=R(N-1)+(R-X) (N=1,2,3,4…)
于是meet从相遇点开始走,head从头节点开始走,head走的长度为L,L=R(N-1)+(R-X) (N=1,2,3,4…),当head到入口E时,meet运动了R-X加上转了(N-1)圈的长度,则两者一定会相遇。
相关文章:

【面试经典题】环形链表
个人主页:一代… 个人专栏:数据结构 在面试中我们经常会遇到有关链表的相关题目,面试官通常会对题目给出拓展 下面我就两个leetcode上的一个双指针的题目为例,并对其进行拓展 题目链接:环形链表 题目描述…...
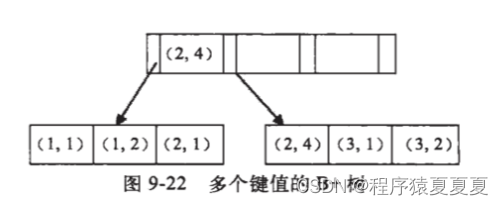
【联合索引】最左匹配原则是什么?
什么是联合索引 联合索引(Composite Index)是一种索引类型,它由多个列组成。 MySQL的联合索引(也称为复合索引)是建立在多个字段上的索引。这种索引类型允许数据库在查询时同时考虑多个列的值,从而提高查询…...
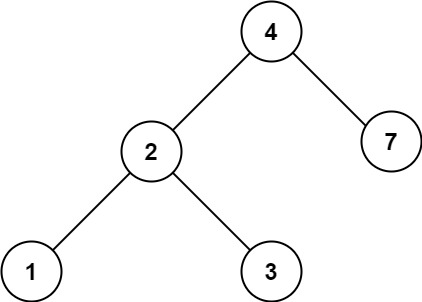
LeetCode 700.二叉搜索树中的搜索
LeetCode 700.二叉搜索树中的搜索 1、题目 题目链接:700. 二叉搜索树中的搜索 给定二叉搜索树(BST)的根节点 root 和一个整数值 val。 你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则…...
 (price 200)(不包含文档))
程序设计实践-课程设计任务布置(麦当劳) (price 200)(不包含文档)
WX: help-assignment code price 200(不包含文档!不包含文档!不包含文档!) 课题任务-概述 2023年5月,麦当劳在北邮开业。大量的学生去那里订餐。正因为如此,麦当劳的在线点餐系统经常关闭以避…...

leetcode 918.环形子数组的最大和
思路:DP 其实和昨天做的哪个重复数组差不多,按顺序来说先做这个题目其实更好。 这里需要分两种情况:第一个,就是数组不越界的时候,这个时候最大子数组和就是leetcode 53题的题解。 如果说越界了,我们还需…...

Spring中用到的设计模式有哪些
工厂模式,BeanFactory就是简单工厂模式的体现,根据传入一个唯一的标识来获得Bean对象。 单例模式,Spring依赖注入Bean实例默认是单例的。Spring依赖注入(包括lazy-init方式)都是发生在AbstractBeanFactory的getBean里。getBean的doGetBean方法调用getSingleton进行bean的创…...

CSS 样式清单整理:文字超出部分显示省略号和设置placeholder的字体样式
单行文本的溢出显示省略号(一定要有宽度) p{width:200rpx;overflow: hidden;text-overflow:ellipsis;white-space: nowrap;}多行文本溢出显示省略号 p {display: -webkit-box;-webkit-box-orient: vertical;-webkit-line-clamp: 3;overflow: hidden;}设…...
Docker容器:Docker-Consul 的容器服务更新与发现
目录 前言 一、什么是服务注册与发现 二、 Docker-Consul 概述 1、Consul 概念 2、Consul 提供的一些关键特性 3、Consul 的优缺点 4、传统模式与自动发现注册模式的区别 4.1 传统模式 4.2 自动发现注册模式 5、Consul 核心组件 5.1 Consul-Template组件 5.2 Consu…...
容器化Jenkins远程发布java应用(方式二:自定义镜像仓库远程拉取构建)
1.创建maven项目 2.配置git、maven 3.阿里控制台>容器镜像服务>镜像仓库>创建镜像仓库 4.执行shell脚本(推送镜像到阿里云镜像仓库) 使用到登录阿里云仓库命令 #!/bin/bash # 服务名称 SERVER_NAMEplanetflix-app # 镜像tag IMAGE_TAG1.0.0-SN…...
解密某游戏的数据加密
前言 最近有个兄弟通过我的视频号加我,咨询能否将这个dubo游戏游戏开始前就将数据拿到从而进行押注,于是通过抓包工具测试了下,发现数据有时候是明文,有时候确实密文,大致看了下有这几种加密:Md5aes、Md5&a…...

【报错合集】完美解决“虚拟机使用的是此版本 VMware Workstation 不支持的硬件版本”
文章目录 解决方案:更改设置的硬件版本 今天我需要将别人的虚拟机克隆到我的VMware Workstation上运行,结果发生了以下的错误: 刚开始以为是VMware Workstation的版本问题太低导致的,所以我删除了原来的那个版本,下载…...

YOLOv8小白中的小白安装环境教程!没一个字废话,看一遍不踩坑!
文章目录 去哪里下代码?怎么下代码?怎么装环境?命令行界面(CLI)指令和Python脚本区别?附录1 conda常用指令附录2 git常用指令附录3 项目代码文件作用去哪里下代码? 下载代码请大家直接去 YOLOv8的官方仓库下载,名字叫 ultralytics,有些镜像网站和个人发的等来历不明的代…...

C#正则表达式,提取信息使用
正则表达式简介 在C#中,正则表达式(Regular Expression,通常简写为regex或regexp)是一种功能强大的文本处理工具,它使用特定的字符序列来定义搜索模式,从而实现对文本的高效搜索、匹配和替换操作。正则表达…...
【数据结构】详解队列
现在我们来掌握一下队列!如果有对往期知识有不足地方,可翻阅之前文章哦! 个人主页:小八哥向前冲~-CSDN博客 所属专栏:数据结构【c语言版】_小八哥向前冲~的博客-CSDN博客 栈和队列的实现其实都是对你顺序表和链表的检验…...

大模型微调方法汇总
微调方法 Freeze方法P-tuning方法 prefix-tuningPrompt TuningP-tuning v1P-tuning v2Lora方法 重要相关参数LoRA 的优势Qlora方法 相关参数微调经验 模型选择模型大小选择数据处理微调方案英文模型需要做词表扩充吗?如何避免灾难遗忘大模型的幻觉问题微调后的输出…...
探究NVMe SSD HMB应用场景与影响-<续>
如果需要采用HMB功能,需要SSD支持NVME协议且NVMe 1.2及以上版本。NVME协议中对HMB对应有2个关键参数: HMB建议值(HMPRE):设定实际分配给HMB使用的主机内存容量,为设备提供最优性能的内存分配量。 HMB最小值…...

YTU 3166 共享单车 DFS 记忆化搜索
问题 D: 共享单车 题目描述 共享单车走进烟台,小明决定尝试。小明启动共享单车 App,轻松地找到附近的单车。那么问题来了,到最近的那辆单车,小明大约要走多少米呢? 现在简化问题。将地图设定成一个由 100100 米的像…...
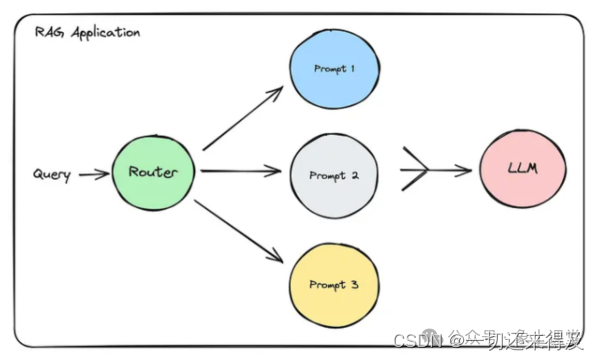
RAG应用中的路由模式
依据的用户查询意图在 RAG 应用程序使用“路由控制模式”可以帮助我们创建更强大的 RAG 应用程序。我们通常希望用户能够访问的数据可以来自各种来源,如报告、文档、图片、数据库和第三方系统。 对于基于业务的 RAG 应用程序,我们可能还希望用户能够与其它业务系统进行交互,…...

运维:SSH常用命令简介
SH,全称为Secure Shell,是建立在应用层和传输层基础上的安全协议。SSH 是目前较可靠,专为远程登录会话和其他网络服务提供安全性的协议。利用 SSH 协议可以有效防止远程管理过程中的信息泄露问题。通过 SSH 可以对所有传输的数据进行加密&…...
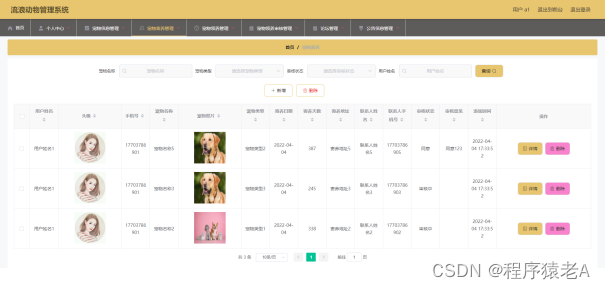
Springboot+Vue项目-基于Java+MySQL的流浪动物管理系统(附源码+演示视频+LW)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:Java毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计 &…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...