自动驾驶决策规划——坐标转换
以下内容来自b站up主忠厚老实的老王,视频链接:自动驾驶决策规划算法序章 总纲与大致目录_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from=333.999.0.0&vd_source=d36e625f376908cfa88ef5ecf2fb0ed8侵删。
https://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from=333.999.0.0&vd_source=d36e625f376908cfa88ef5ecf2fb0ed8侵删。
决策规划算法概述



数学基础
五次多项式


 其中隐含的限制就是f(t)的定义域和值域都应该是实数,因为s和t都是真实空间中的轨迹和时间坐标,不能有虚数。
其中隐含的限制就是f(t)的定义域和值域都应该是实数,因为s和t都是真实空间中的轨迹和时间坐标,不能有虚数。
要想使得上面的那个jark最小,积分号中是平方项,也就是当其为0时最小,也就是f(t)的三阶导数为0,也就是f(t)是二次或者二次以下的函数时,三阶导数才为0。





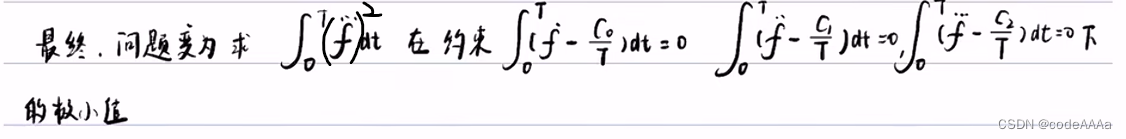
也就是求泛函![]() 在后面的那三个约束条件下极小值对应的f(t)。
在后面的那三个约束条件下极小值对应的f(t)。


上面把一个带约束的泛函化成了一个无约束的泛函,但是L和f点、f两点、f三点都有关,不能直接使用上面只能处理一阶导数的欧拉——拉格朗日方程。要使用广义的欧拉——拉格朗日方程:

 凸优化
凸优化



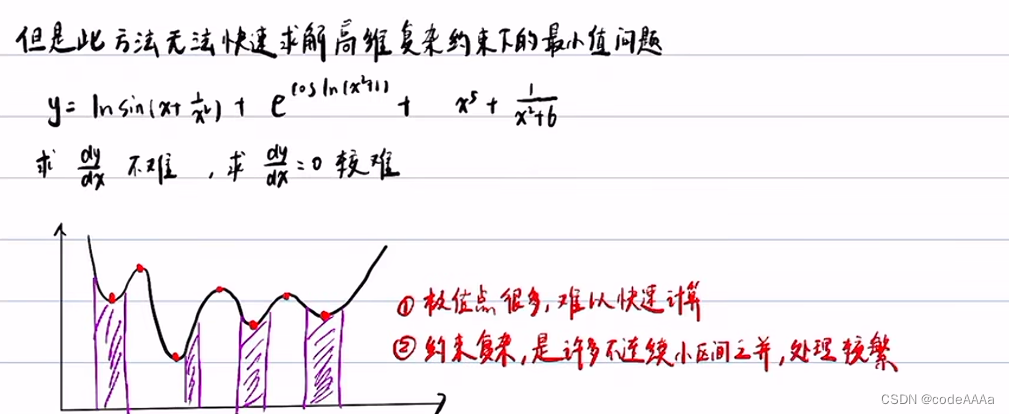
所以一般求复杂函数在复杂约束条件下的最小值问题都采用迭代法。迭代法的求解速度要比求导法快很多。

以梯度下降法为例说明大概原理:

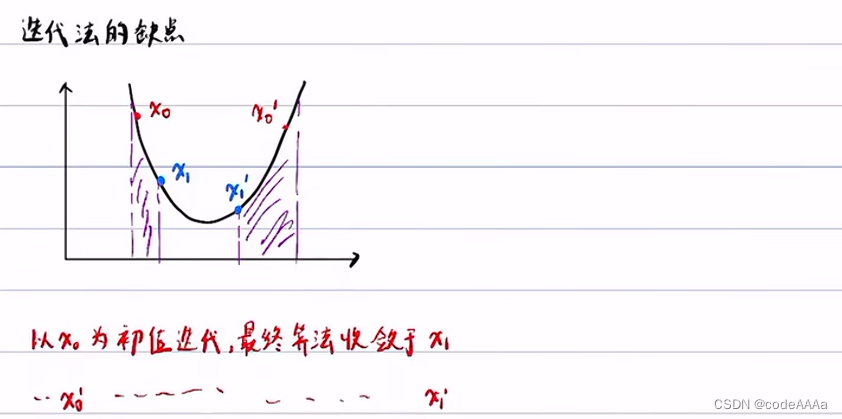
 紫色区域是约束,所以迭代法对初值比较敏感,有可能收敛到局部最小值。
紫色区域是约束,所以迭代法对初值比较敏感,有可能收敛到局部最小值。
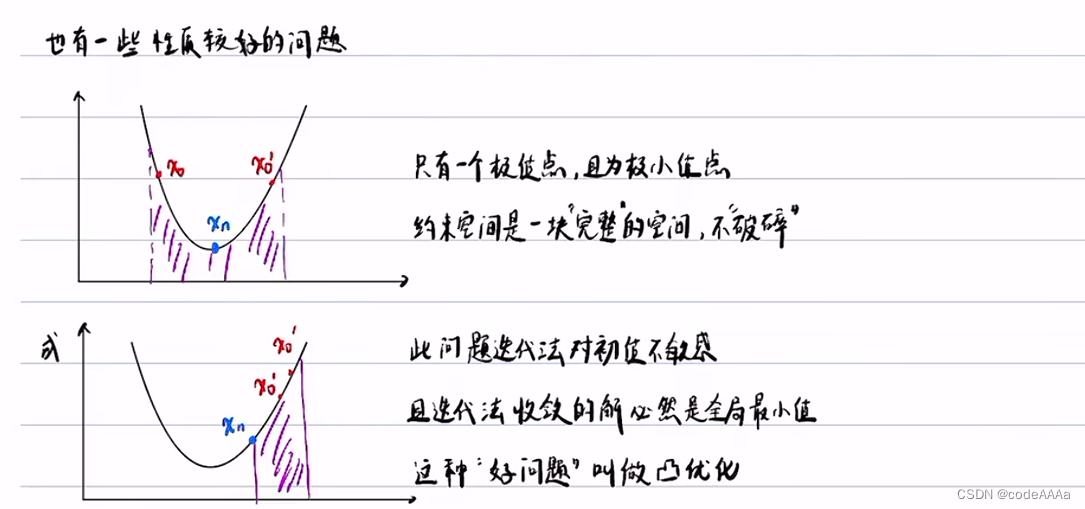



凸优化是最简单的非线性规划方法。自动驾驶的规划求解不是一个凸优化问题,凸优化必须满cost function是一个凸函数,约束空间是一个凸空间,以避障工况为例:



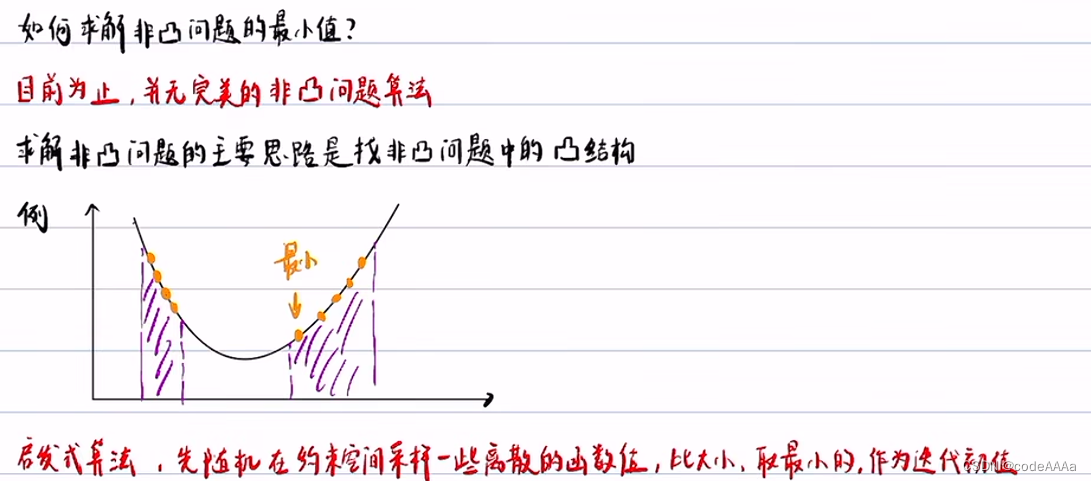
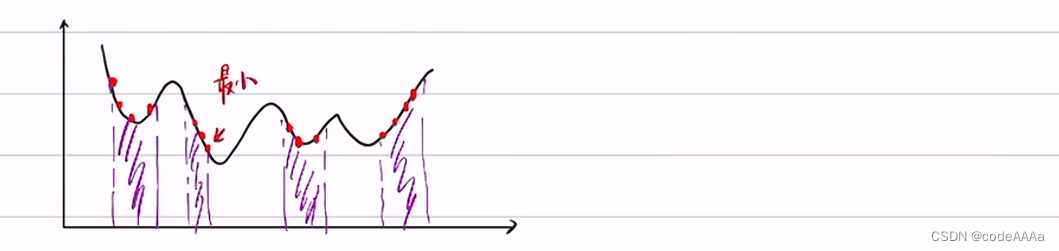
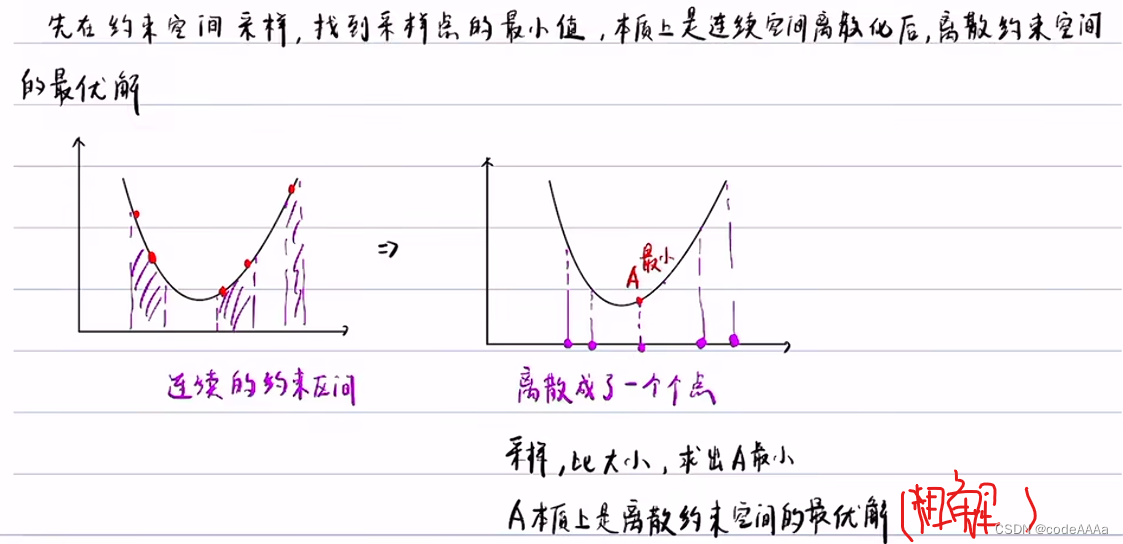
整个过程就是:

上述方法也有一定的缺点:

采样点少的话会比较容易收敛到局部最优,采样点多的话会发生维度灾难,如下:
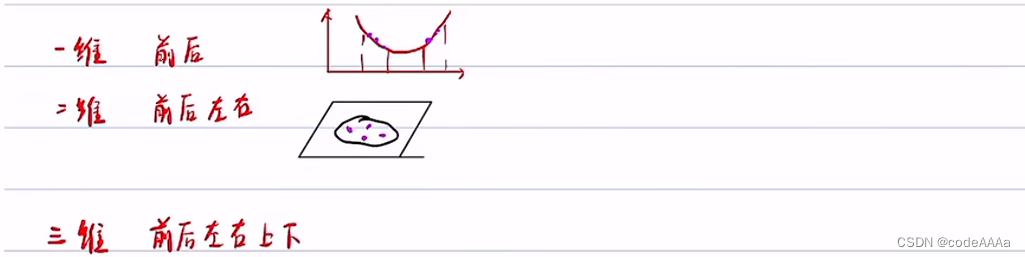
frenet坐标系和Cartesian坐标系坐标转换
概述和基本量





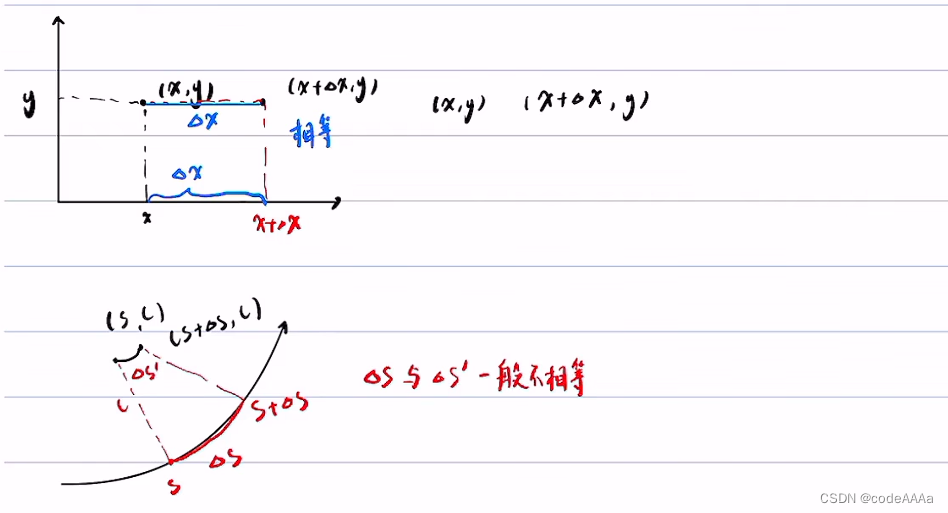

也就是在直角坐标系下想对一个函数求导,那它只有一个dx,这个dx是不区分点在x坐标上的位移还是点的实际位移在x坐标上的分量,因为这两者一样;但是在frenet坐标系中,它们是一样的所以在frenet坐标系中会有d/ds和d/dsx之分。在直角坐标系中可能只有一个dx,但是在frenet坐标系中,可能会有多个ds,举例说明如下:

这里使用dsx和ds来区分不同的s,在很多推导教程中可能中只用ds,会造成理解困难。
预备知识1

证明这个质点位矢r的导数等于v的模乘以τ,τ是质点在切线方向的单位向量。

当dt趋近于0时,ds和dr无限的接近,比值为1,方向会无限的趋近于在位矢r处的切线方向,也就是τ。
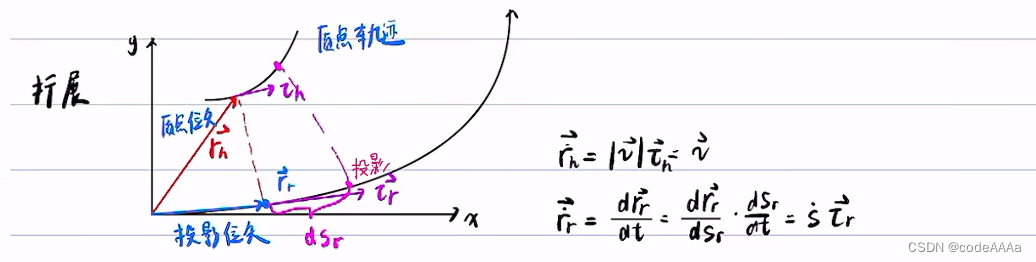
 预备知识2:frenet坐标系
预备知识2:frenet坐标系

其中ds是黑色曲线的弧微分,证明如下:

其中τ+dτ和τ以及dτ形成的三角形是一个等腰三角形,可以求出dτ的大小(也即使dτ的模),方向趋近于τ的法线方向。
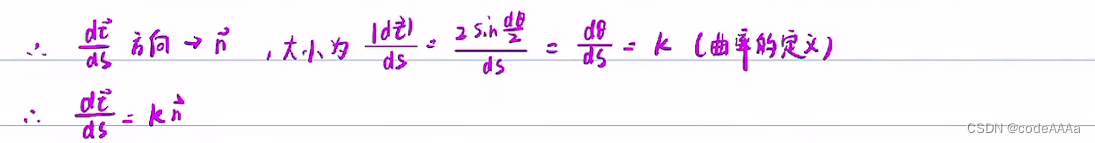 其中当dτ无限趋近于0时,sin(dθ/2)等价无穷小于(dθ/2)。
其中当dτ无限趋近于0时,sin(dθ/2)等价无穷小于(dθ/2)。
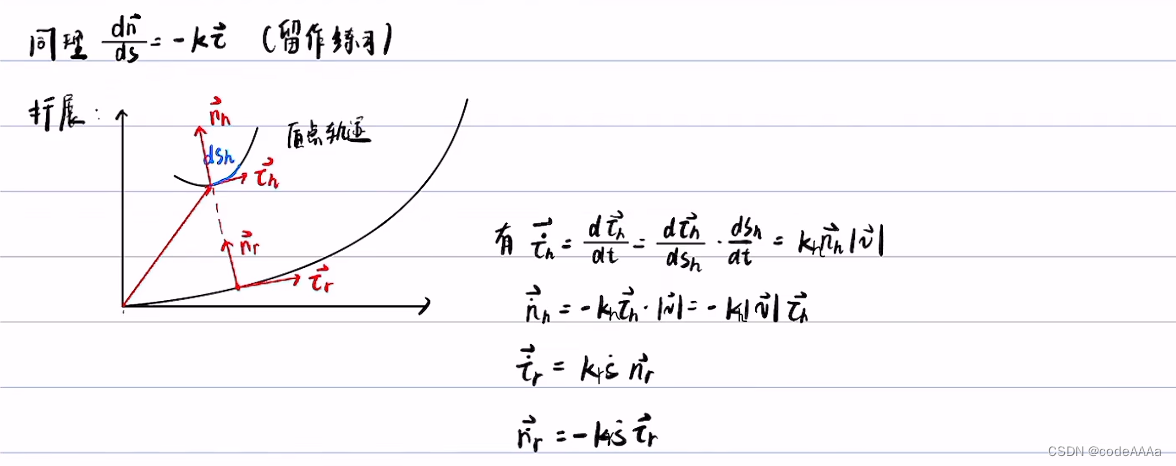
其中 kh是质点轨迹的曲率,kr是道路中心线的曲率,这里的曲率都是在直角坐标系下的曲率。

这里的ds指的是frenet坐标轴下的弧微分。

其中ρ是曲率半径,法向加速度是向心加速度。
预备知识总结
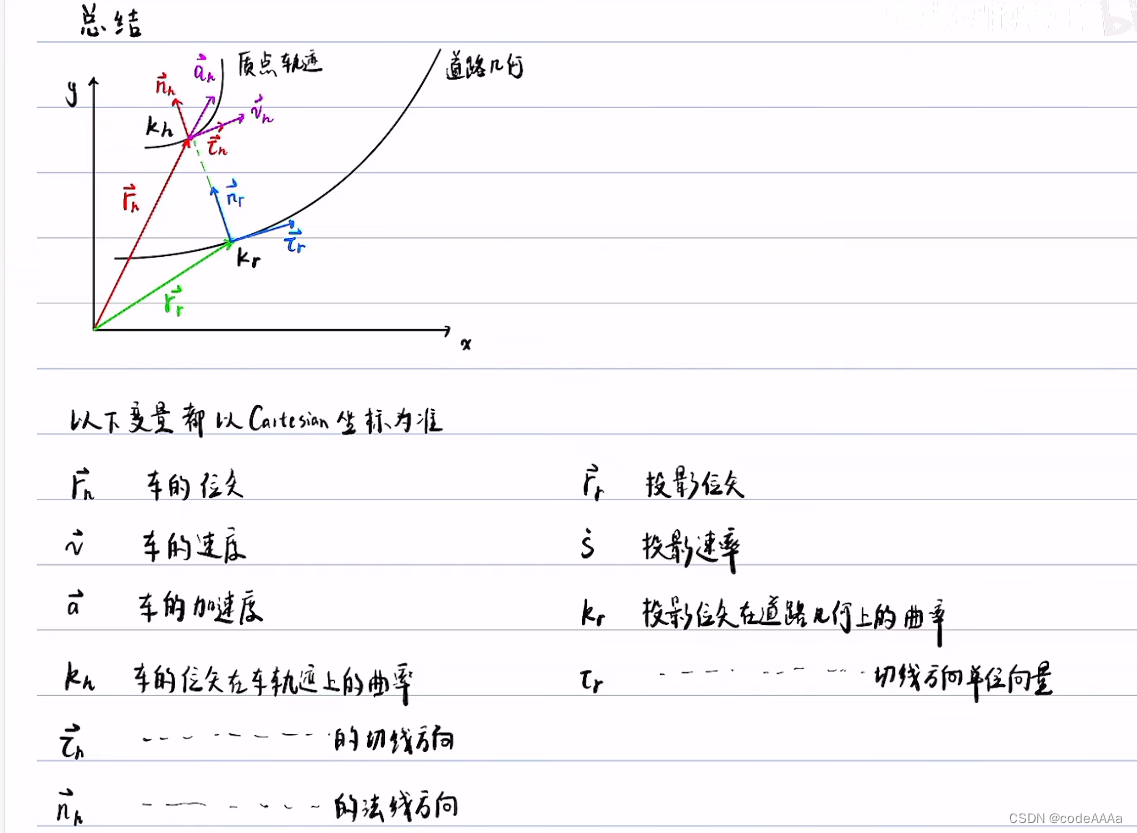


坐标转换(从直角坐标转为frenet坐标)
下面的问题就是已知在笛卡尔坐标系下的![]() ,以及frenet坐标系下的坐标起点
,以及frenet坐标系下的坐标起点![]() ,算这个点在frenet坐标系下的
,算这个点在frenet坐标系下的![]() ,其中
,其中![]() 。
。

其中向量三角形是黄色区域,由向量三角形可以得到核心的公式:
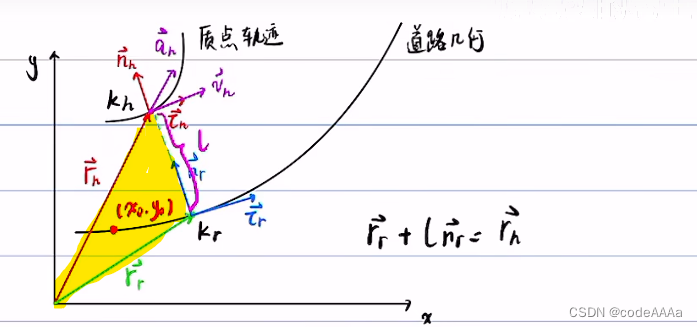
得到上面的核心公式,可以该公式和微积分依次求出![]() ,但是这个公式还不能直接使用,因为只知道rh,rr和nr未知,此时要找到投影点的相关信息。
,但是这个公式还不能直接使用,因为只知道rh,rr和nr未知,此时要找到投影点的相关信息。
投影点及其相关的信息的确定方法如下:

最后计算得到rr的原理如下:

为什么可以![]() 原理如下:
原理如下:


至此投影点的信息已经基本求值完毕。
下面可以使用上面的核心公式来计算相关量。
s的计算方法是从离散规划点起点开始把各个点的长度累加起来一直累加到投影点(xr,yr)为止。也就是以直线长度近似代替弧长:


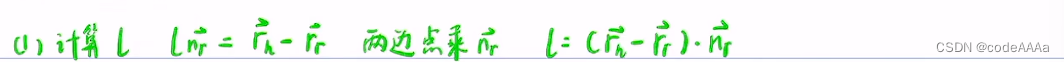

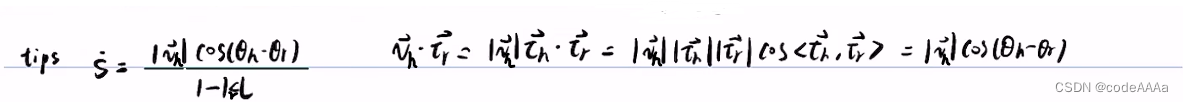




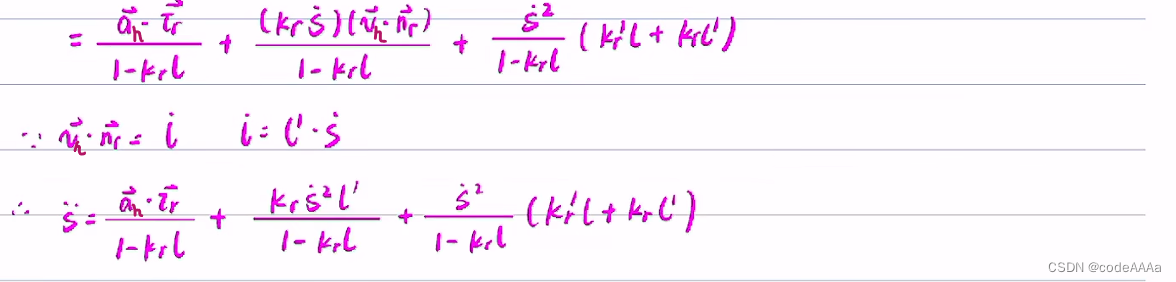

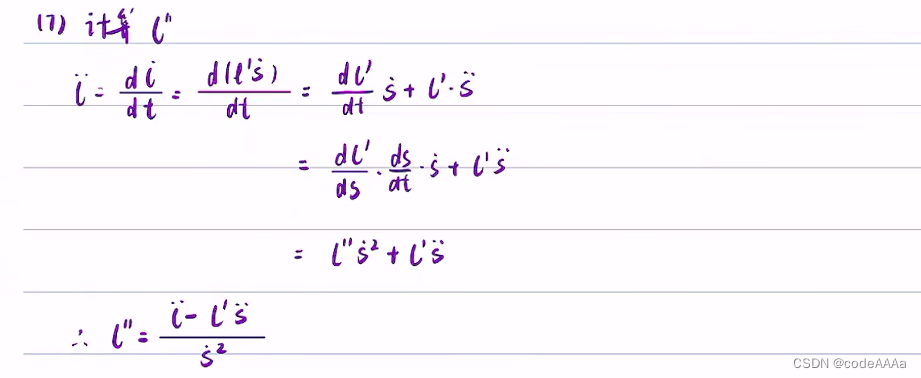
小结
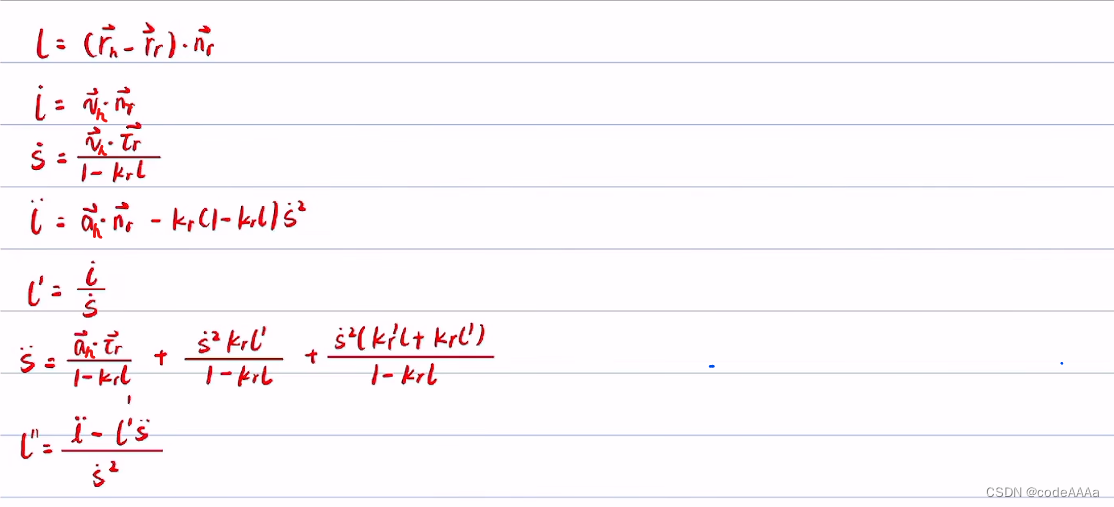
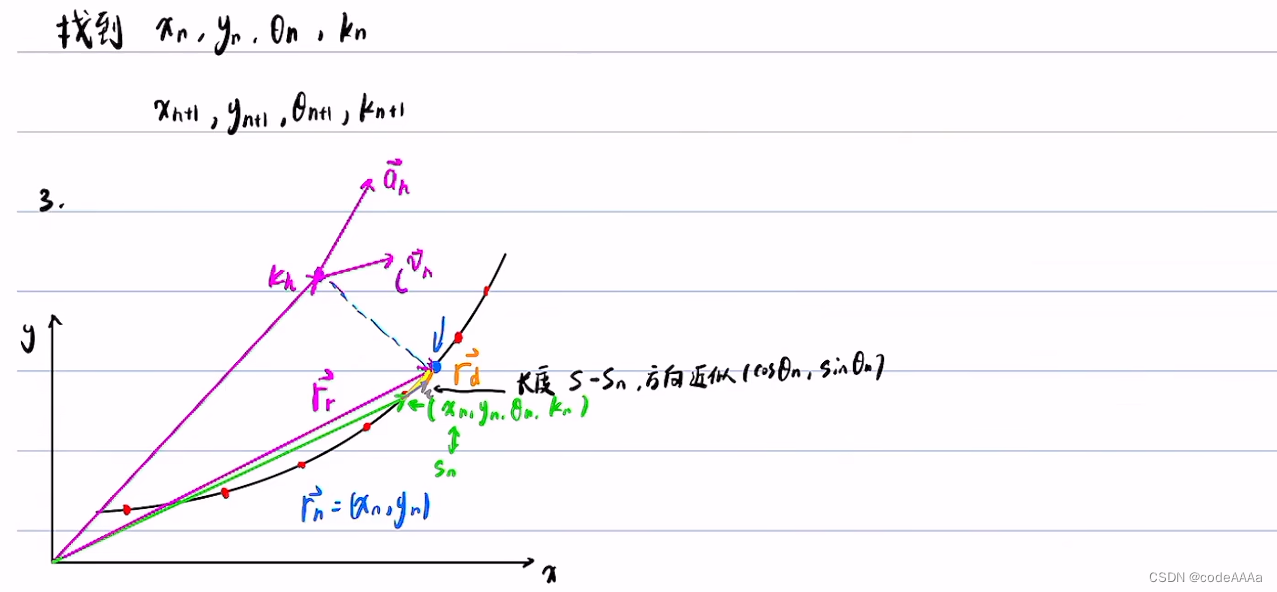
坐标变换(从frenet转换到直角坐标)



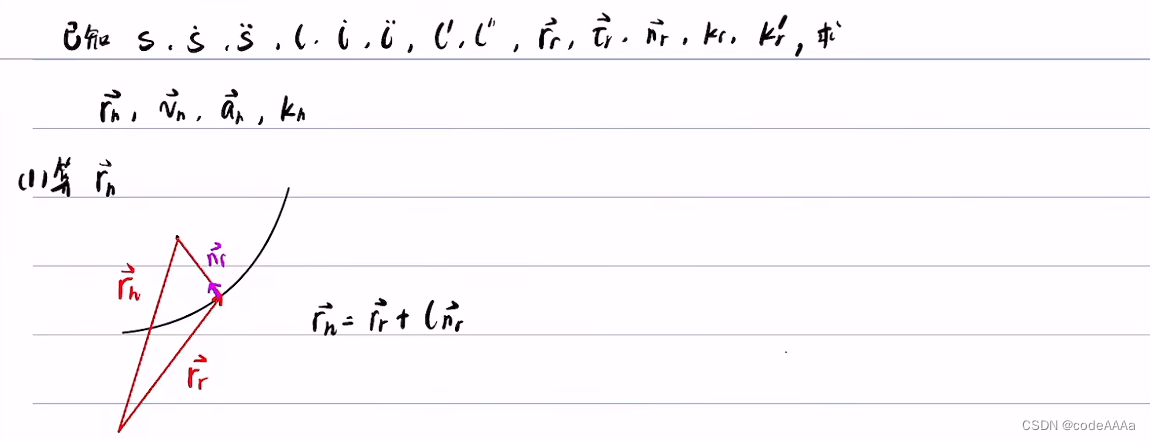
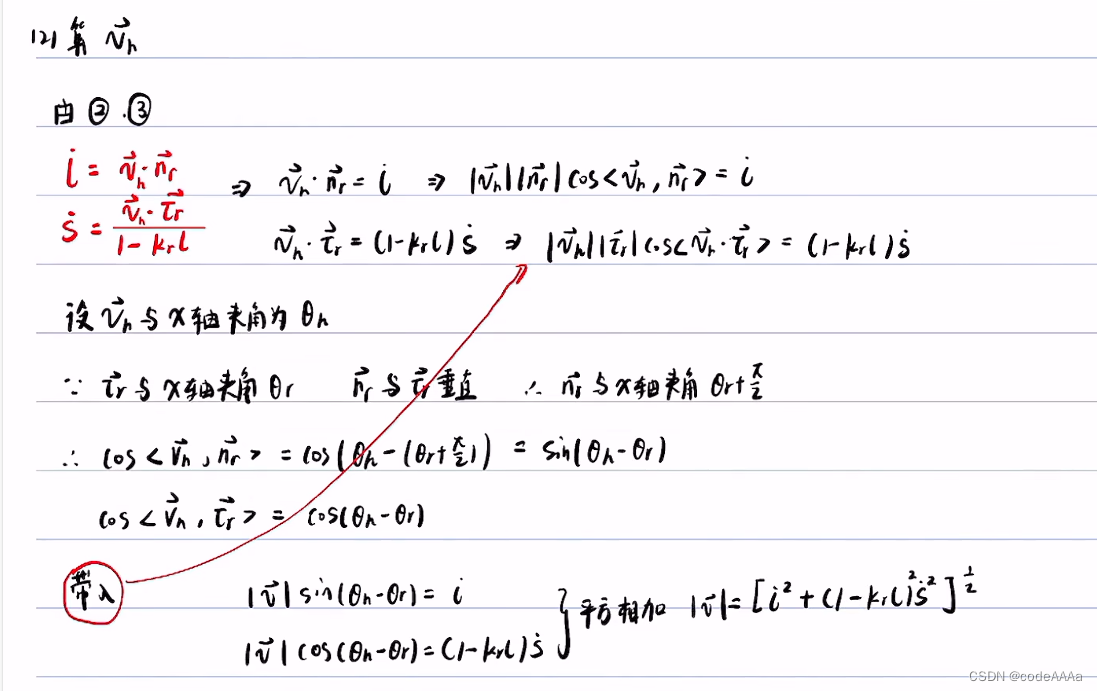
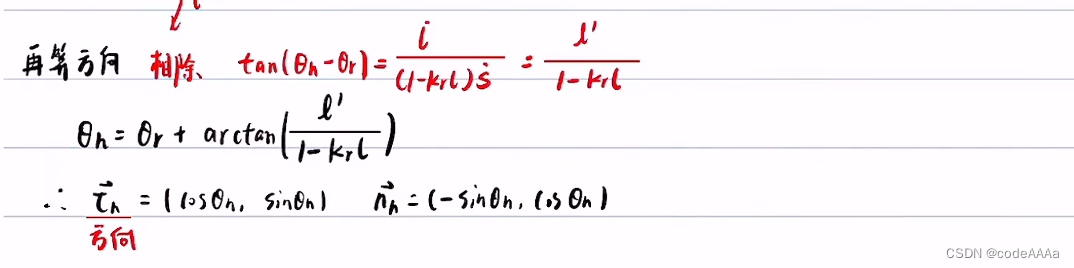
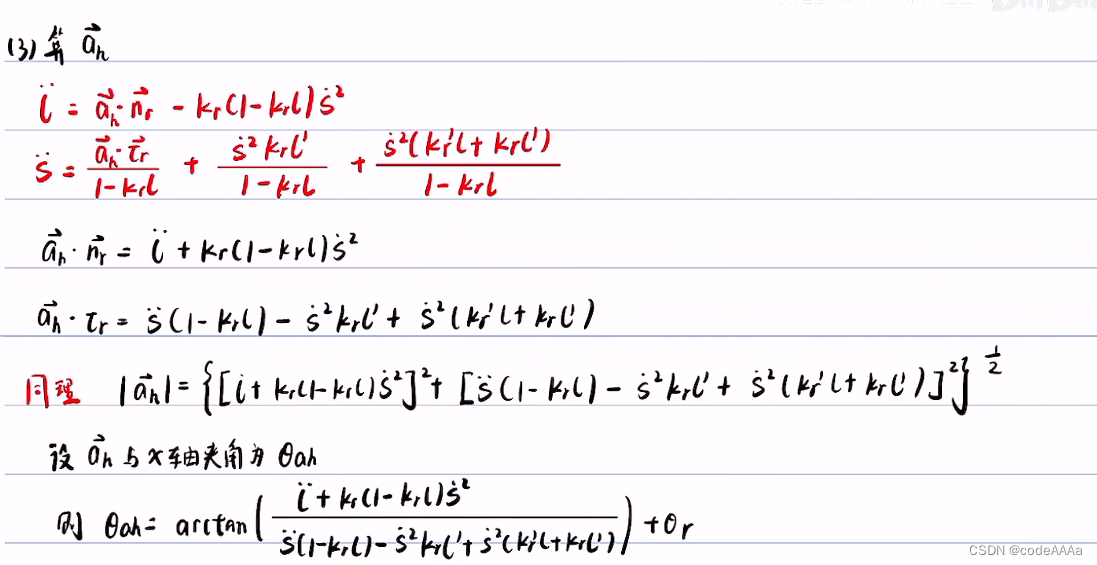

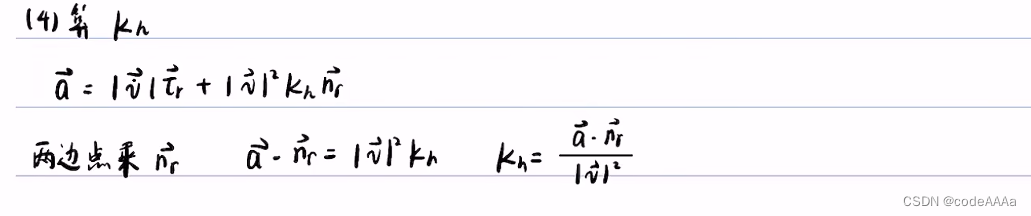
相关文章:
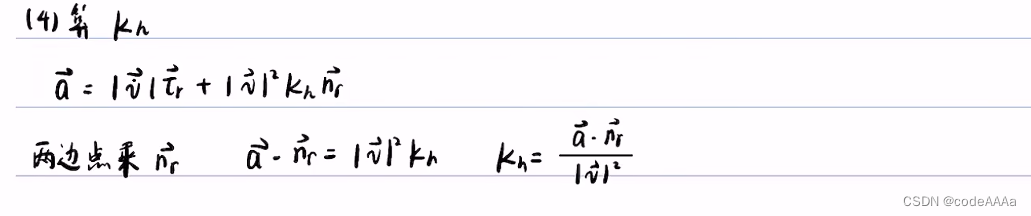
自动驾驶决策规划——坐标转换
以下内容来自b站up主忠厚老实的老王,视频链接:自动驾驶决策规划算法序章 总纲与大致目录_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1hP4y1p7es/?spm_id_from333.999.0.0&vd_sourced36e625f376908cfa88ef5ecf2fb0ed8侵删。 决策规划算法…...

信创应用软件之邮箱
信创应用软件之邮箱 文章目录 信创应用软件之邮箱采用信创邮箱的必要性信创邮箱采购需求国产邮箱业务形态国产邮箱代表性品牌CoremailRichmail安宁eyouUMail拓波 邮件安全的发展阶段 采用信创邮箱的必要性 邮箱是天然的数据存储空间,党政和央国企客户在使用过程中存…...
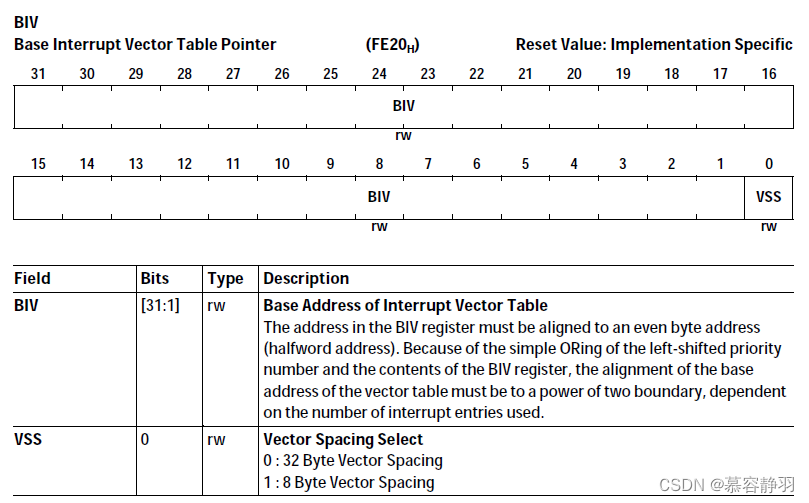
TriCore: Architecture
说明 本文是 英飞凌 架构文档 TriCore TC162P core archiecture Volume 1 of 2 (infineon.com) 的笔记,稍作整理方便查阅,错误之处,还请指正,谢谢 :) 1. Architecture 2. General Purpose & System Register 名词列表&#…...

16进制与不同进制之间计算加减乘除的比较快的方法
方法: 1.加分、减法: 将所有的进制的数转成目标进制的数,然后按位加。 如 0x123 0x1234 0x1357 2.乘法、除法: 将所有的进制的数转成二进制数,然后进行移位。 如 0x123456 乘 32(十进制)…...

责任链模式:原理与实现解析,及其应用场景代入
责任链模式的作用:复用和扩展,在实际的项目开发中比较常用,特别是框架开发中,我们可以利用它们来提供框架的扩展点,能够让框架的使用者在不修改框架源码的情况下,基于扩展点定制化框架的功能。 这里主要介…...

从心理学角度看,GPT 对人有什么影响?
开启个性化AI体验:深入了解GPT的无限可能 导言 GPT 与我们日常生活的融合标志着技术进步的重大飞跃,为提高效率和创新提供了前所未有的机遇。然而,当我们与这些智能系统日益紧密地交织在一起时,探索它们对个人产生的细微的心理影响…...
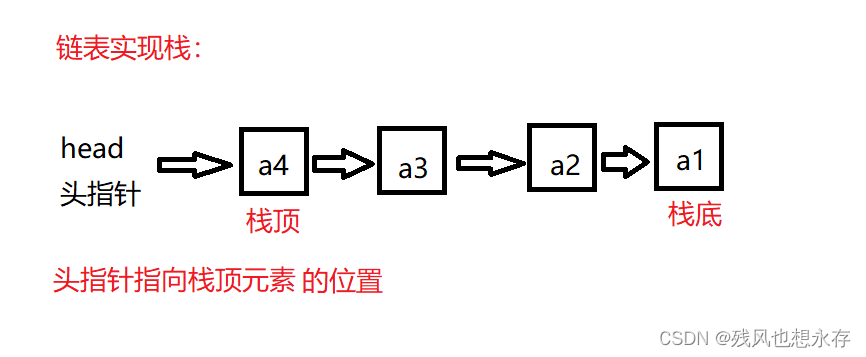
【C语言/数据结构】栈:从概念到两种存储结构的实现
目录 一、栈的概念 二、栈的两种实现方式 1.顺序表实现栈 2.链表实现栈 三、栈的顺序存储结构及其实现 1.栈的声明 2.栈的初始化 3.栈的销毁 4.栈的压栈 5.栈的弹栈 6.栈的判空 7.返回栈顶元素 8.返回栈的长度 四、栈的链式存储结构及其实现 1.栈的声明 2.栈的…...

47. UE5 RPG 实现角色死亡效果
在上一篇文章中,我们实现了敌人受到攻击后会播放受击动画,并且还给角色设置了受击标签。并在角色受击时,在角色身上挂上受击标签,在c里,如果挂载了此标签,速度将降为0 。 受击有了,接下来我们将…...

C语言/数据结构——每日一题(环形链表)
一.前言 今天在力扣上刷到一道链表题——环形链表https://leetcode.cn/problems/linked-list-cycle 想着和大家们分享一下。让我们直接开始今天的分享吧。、 二.正文 1.1题目描述 1.2题目分析 这道题是想让我们做出分析,该链表是不是带环链表,如果是…...

vue:网页icon无法显示
logo文件放在public文件夹下,在html里设置icon。 本地源码运行后发现网页icon无法显示我们设置的logo,而是显示了浏览器默认icon。 这个问题不需要解决,部署后网页icon显示就正常了。...

电脑设置在哪里打开?Window与Mac双系统操作指南
随着科技的不断发展,电脑已经成为我们日常生活和工作中不可或缺的一部分。然而,对于许多初学者来说,如何找到并熟悉电脑的设置界面可能是一个挑战。特别是对于那些同时使用Windows和Mac双系统的用户来说,更是需要一篇详尽的指南来…...
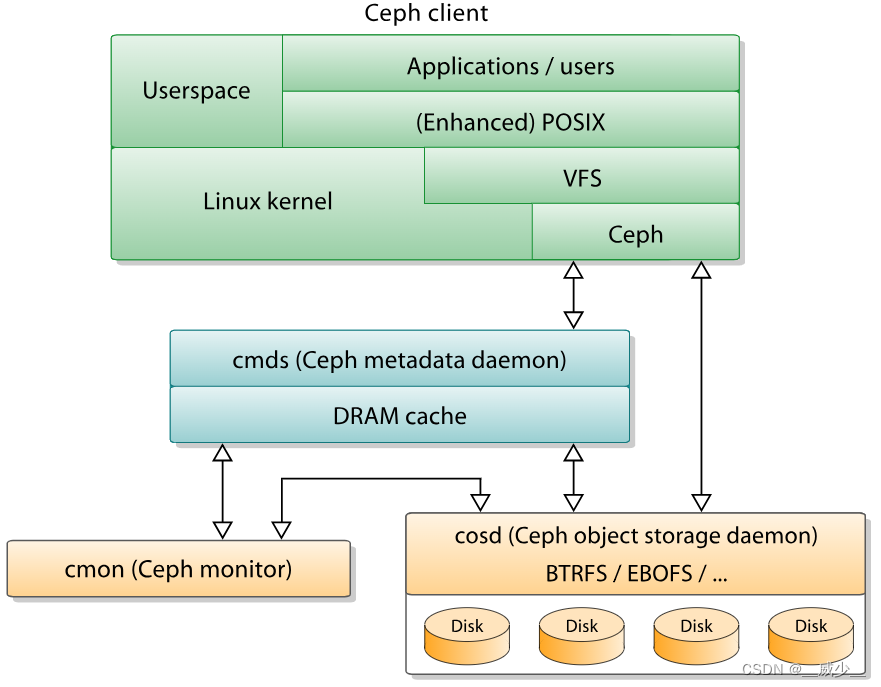
【linux】海量小文件的存储方案
在介绍海量文件存储之前,需要先介绍一下常见的系统里面文件是如何存储的 文件inode 在linux下,每个文件或者目录,都会分配一个inode(index node),它不存储具体的文件内容,而是记录该文件的基础信息。每个inode大小一…...
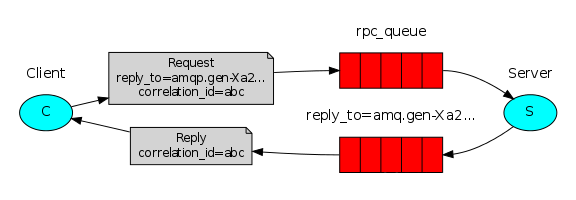
【SpringBoot整合系列】SpringBoot整合RabbitMQ-基本使用
目录 SpringtBoot整合RabbitMQ1.依赖2.配置RabbitMQ的7种模式1.简单模式(Hello World)应用场景代码示例 2.工作队列模式(Work queues)应用场景代码示例手动 ack代码示例 3.订阅模式(Publish/Subscribe)应用…...

MySQL————创建存储过程函数
存储过程使用大纲 有参数传递 delimiter $$ 声明一个名称为get_student_introduce create procedure add_student_infor( in p_userName VARCHAR(20),in p_phone VARCHAR(11),in p_sex char(2),in p_introduce VARCHAR(255)) 开始操作 BEGIN 撰写真正在操作DMLDQL都行 INSE…...
——数据要素:管理核心框架)
数据赋能(86)——数据要素:管理核心框架
数据管理的核心框架是一个综合性的体系,旨在确保数据的有效利用、安全性以及合规性。这个框架主要包含了以下几个关键组成部分: 数据治理策略与目标:明确数据管理的整体战略和目标,包括数据价值的释放、数据资产地位的确定、多元…...
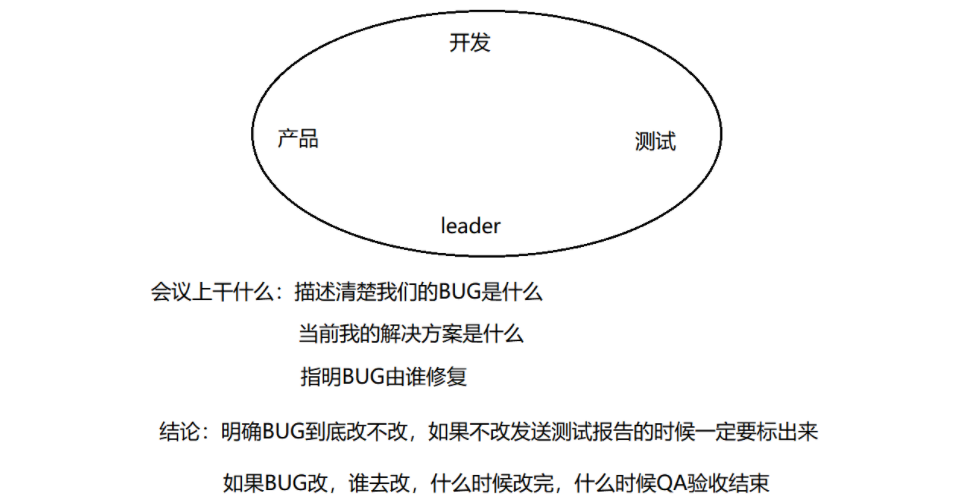
测试的基本概念
什么是软件测试 软件测试它就是一个过程测试就是对软件的全方位进行全面的校验.通过测试技术验证软件是不是符合用户的信息. 测试和开发的区别 在工作上的区别: 开发人员通过编程技能来开发和实现这个软件. 测试人员通过测试技能来验证软件是否符合用户需求. 在技术上的要求…...

Python多线程加速-休眠部分线程
总所周知Python由于GIL的问题,使用多线程时同一时刻只有一个线程在工作。故Python会在所有线程之间不断的切换,每切换到一个线程会执行一段字节码指令然后切换到另一个线程。如果开启了很多线程,且只有小部分线程在工作,如果不休眠…...
)
B+树(B+ Tree)
B树(B Tree)是一种对B树(B-Tree)的改进版本,它在数据库系统和文件系统中作为索引结构得到了广泛的应用,特别是在磁盘存储的场景下。B树保留了B树的基本特征,如自平衡、多路分支等,但…...

【Linux】了解信号产生的五种方式
文章目录 正文前的知识准备kill 命令查看信号man手册查看信号信号的处理方法 认识信号产生的5种方式1. 工具2. 键盘3. 系统调用kill 向任意进程发送任意信号raise 给调用方发送任意信号abort 给调用方发送SIGABRT信号 4. 软件条件5. 异常 正文前的知识准备 kill 命令查看信号 …...

【nuxt3国际化i18n】vue3+nuxt3+vite+TS国际化的正确做法
1、创建nuxt3请看Nuxt3官网 2、下面是添加i18n的叫教程,适用于企业前端项目。 添加依赖 依赖 yarn add vue-i18n yarn add nuxtjs/i18nnext -D配置文件nuxt.config.ts //nuxt.config.ts export default defineNuxtConfig({modules: [nuxtjs/i18n,],i18n: {stra…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
