【思维】根号分治
写在前面的话:
个人理解 根号分治本身就是一种卡着评测机过题的做法,所以非必要不要写 #define int long long !!!
本篇博客参考:暴力美学——浅谈根号分治
做到过两三题根号分治了,来总结一下这个算法
与其说是算法,不如说是一种思维
根号分治的主要思路是,数据范围很大的时候(指不能接受 n 2 n^2 n2 复杂度,但可以接受 n n n\sqrt n nn 复杂度的情况,通常是 1 e 8 − 1 e 9 1e8-1e9 1e8−1e9),将数据分为两个部分,一个是小于 n \sqrt n n 的部分,一个是大于等于 n \sqrt n n 的部分,两个部分分别采用不同的处理方式:
- 第一个部分(需要处理的间隔小的部分),使用技巧计算,例如前缀和等预处理算法
- 第二个部分(需要处理的间隔大的部分),暴力计算
下面举例说明几个可以使用根号分治的场景
- 数据结构
- 数论
数据结构
来一道例题:F. Remainder Problem
题目意思是,给出一个长度为 5 e 5 5e5 5e5 的序列,初始值都是 0,给出 q 组操作,每组操作包括 op x y:
op == 1时,a[x] += yop == 2时,输出下标模x等于y的位置的值之和
我们可以想到两种做法:
- 暴力处理,第一个操作就直接加,复杂度 O ( 1 ) O(1) O(1),第二个操作就遍历一遍数组,复杂度 O ( n ) O(n) O(n),这样最坏的复杂度是 O ( n q ) O(nq) O(nq),T
- 利用二维数组预处理,
b[i][j]表示模i等于j的位置上的值之和,第一个操作就遍历更新b[i][j],复杂度 O ( n ) O(n) O(n),第二个操作直接输出,复杂度 O ( 1 ) O(1) O(1),最坏的复杂度是 O ( n q ) O(nq) O(nq),T
那能不能把两者结合起来呢?
我们发现如果 x 比较大的话,暴力处理的第二个操作复杂度就不会太高,但是不能进行预处理(空间上不能接受),x 比较小的话,可以进行预处理,而暴力操作的复杂度就会比较高
说到这里就清楚啦:x 大就第一个做法,x 小就第二个做法,大小的分界线是什么呢?就是 n \sqrt n n
c o d e code code
#include <bits/stdc++.h>using namespace std;// #define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 5e5 + 10;
const int maxn = 710;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;int a[N], b[710][710];void solve()
{int q;cin >> q;while (q -- ){int op, x, y;cin >> op >> x >> y;if (op == 1){a[x] += y;for (int i = 1; i < 700; i ++ ) b[i][x % i] += y;}else{if (x < 700) cout << b[x][y] << '\n';else{int res = 0;for (int i = y; i <= 5e5; i += x) res += a[i];cout << res << '\n';}}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
数论
看这题:D. Two Arithmetic Progressions
题目给出这样的两个数列:
- a 1 k + b 1 a_1k+b_1 a1k+b1
- a 2 k + b 2 a_2k+b_2 a2k+b2
k > = 0 k>=0 k>=0
然后给出 [ l , r ] [l,\ r] [l, r],问这个区间里有多少数同时存在于上面的两个数列里( a 、 b a、b a、b 的范围都是 2 e 9 2e9 2e9)
我们还是想出两种办法:
- k 从 0 开始,枚举第一个数列的数,直到找到一个在第二个数列里也出现的数(可以发现最多找
max(a1, a2)次),之后每次加上循环节(也就是 a 1 a_1 a1 和 a 2 a_2 a2 的最小公倍数)即可 - 枚举 a a a 值较大的数列,符合条件就答案+1,完全暴力
设 maxx = max(a1, a2)
-
当 maxx 比较大的时候,数列里的值的数量就会比较少,可以通过枚举解决问题,但使用第一种方法就会T
-
当 maxx 比较小的时候,枚举会T,但可以使用第一种找循环节的方法
所以通过这个进行根号分治,结束!
(其实这题的正解并不是根号分治,但是使用这种思想可以直接碾过去cf2500的题!!好爽ovo)
c o d e code code
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 2e9;
const int maxn = 710;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int a1, b1, a2, b2, l, r;cin >> a1 >> b1 >> a2 >> b2 >> l >> r;int maxx = max(a1, a2);if (maxx < sqrt(N)) // 找最小公倍数{for (int i = 0; i <= maxx; i ++ ){int tmp = a1 * i + b1;if (abs(tmp - b2) % a2 == 0){int lcmm = lcm(a1, a2);int st = max({l, b1, b2});if (tmp < st){tmp += ((st - tmp) / lcmm + 1) * lcmm;tmp = st + (tmp - st) % lcmm;}else tmp = st + (tmp - st) % lcmm;if (tmp > r) continue;cout << (r - tmp) / lcmm + 1 << '\n';return;}}cout << 0 << '\n';}else // 暴力{int ans = 0;if (a1 < a2) swap(a1, a2), swap(b1, b2);for (int i = b1; i <= r; i += a1){if (i < l || i < b2) continue;if ((i - b2) % a2 == 0) ans ++ ;}cout << ans << '\n';}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
相关文章:

【思维】根号分治
写在前面的话: 个人理解 根号分治本身就是一种卡着评测机过题的做法,所以非必要不要写 #define int long long !!! 本篇博客参考:暴力美学——浅谈根号分治 做到过两三题根号分治了,来总结一下…...
Linux线程(三)死锁与线程同步
目录 一、什么是死锁 死锁的四个必要条件 如何避免死锁 避免死锁算法 二、Linux线程同步 三 、条件变量 1、条件变量基本原理 2、条件变量的使用 3、条件变量使用示例 为什么 pthread_cond_wait 需要互斥量? 一、什么是死锁 死锁是计算机科学中的一个概念,…...
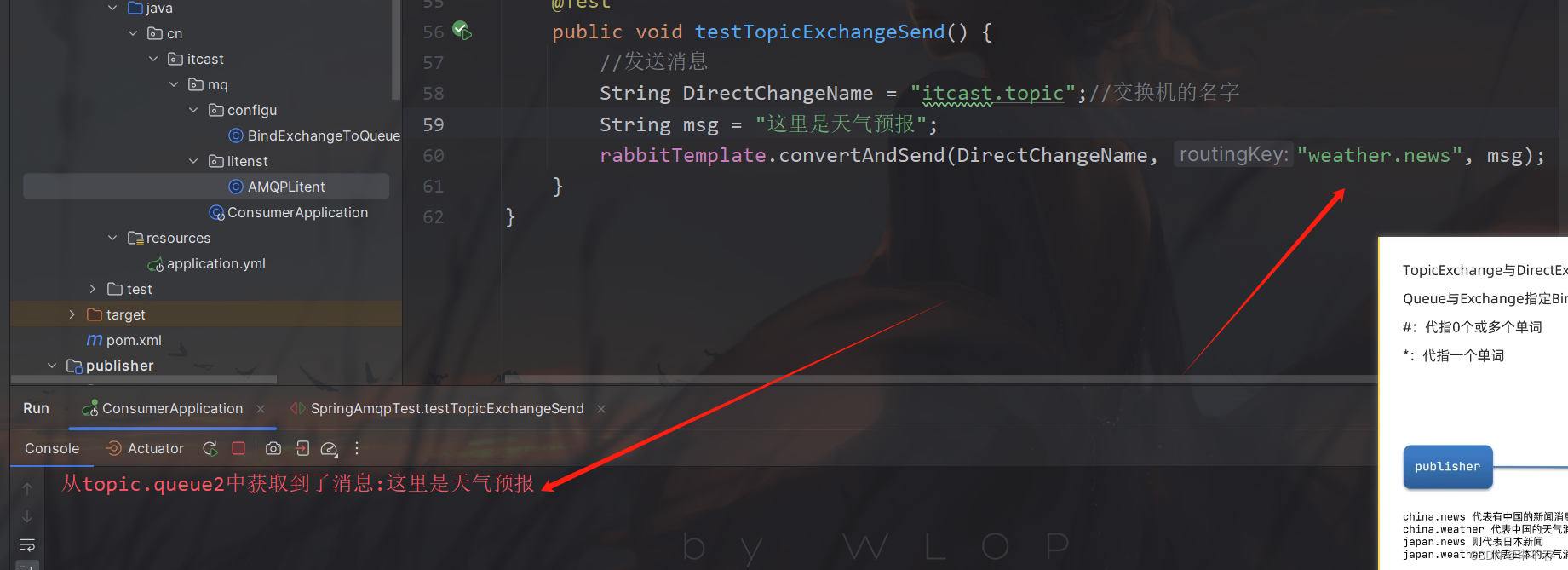
SpringAMQP 发布订阅-TopicExchange
根据这个模型编写代码: RabbitListener(bindings QueueBinding(value Queue(name "topic.queue1"),exchange Exchange(name "itcast.topic",type ExchangeTypes.TOPIC),key {"china.#"}))public void listenTopicQueue1(String msg){Syst…...
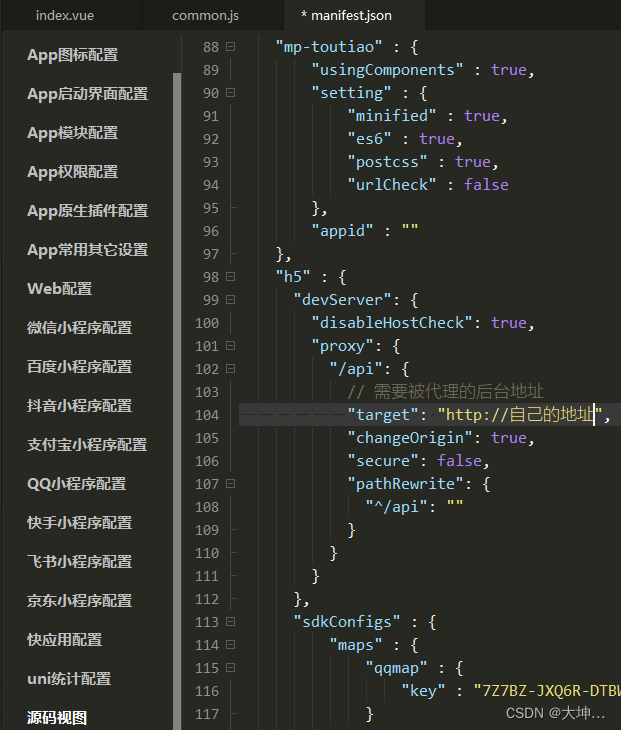
uniapp h5 配置代理服务器
"devServer": {"disableHostCheck": true,"proxy": {"/api": {// 需要被代理的后台地址"target": "http://自己的地址","changeOrigin": true,"secure": false,"pathRewrite": {&q…...

使用Apache Spark从MySQL到Kafka再到HDFS的数据转移
使用Apache Spark从MySQL到Kafka再到HDFS的数据转移 在本文中,将介绍如何构建一个实时数据pipeline,从MySQL数据库读取数据,通过Kafka传输数据,最终将数据存储到HDFS中。我们将使用Apache Spark的结构化流处理和流处理功能&#…...

一篇文章拿下Redis 通用命令
文章目录 Redis数据结构介绍Redis 通用命令命令演示KEYSDELEXISTSEXPIRE RedisTemplate 中的通用命令 本篇文章介绍 Redis 的通用命令, 通用命令在 Redis 的所有数据类型下都使用, 学好通用命令可以让我们更好的使用 Redis. Redis数据结构介绍 Redis 是一个key-value的数据库&…...

锂电池充电充放电曲线分析
前言 锂电池的充电曲线通常包括三个阶段:恒流充电阶段、恒压充电阶段和滞后充电阶段。在恒流充电阶段,电流保持恒定,电压逐渐增加;在恒压充电阶段,电压保持恒定,电流逐渐减小;在滞后充电阶段,电流进一步减小,电池开始充满。通过监测这些阶段的电流和电压变化,可以评…...
)
vue3 第二十九节 (vue3 事件循环之nextTick)
引言 vue 项目中为什么要使用 nextTick 这个函数,是做什么用的,解决了哪些问题 1、nextTick 作用 用于处理DOM更新完成之后,执行回调函数的方法; 2、实现方案 vue2 中 nextTick() 是基于浏览器的 异步队列和微任务队列而执行…...

使用Flask-SocketIO构建实时Web应用
文章目录 准备工作编写代码编写HTML模板运行应用 随着互联网的发展,实时性成为了许多Web应用的重要需求之一。传统的HTTP协议虽然可以实现实时通信,但是其长轮询等机制效率低下,无法满足高并发、低延迟的需求。为了解决这一问题,诞…...
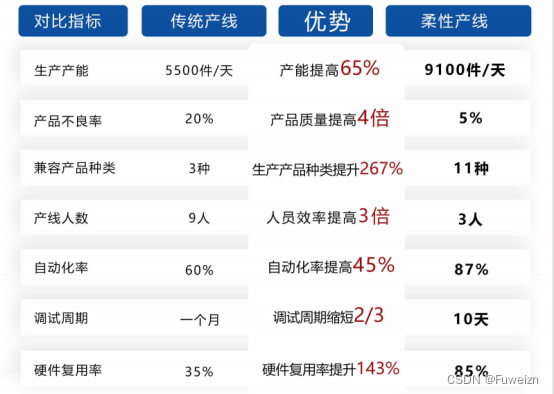
可重构柔性装配产线:为工业制造领域注入了新的活力
随着科技的飞速发展,智能制造正逐渐成为引领工业革新的重要力量。在这一浪潮中,可重构柔性装配产线以其独特的技术优势和创新理念,为工业制造领域注入了新的活力,开启了创新驱动的智能制造新篇章。 可重构柔性装配产线是基于富唯智…...
懒人网址导航源码v3.9
测试环境 宝塔Nginx -Tengine2.2.3的PHP5.6 MySQL5.6.44 为防止调试错误,建议使用测试环境运行的php与mysql版本 首先用phpMyAdmin导入数据库文件db/db.sql 如果导入不行,请直接复制数据库内容运行sql语句也可以 再修改config.php来进行数据库配置…...
)
springboot 开启缓存 @EnableCaching(使用redis)
添加依赖 pom.xml <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency>application.yml 配置redis连参数 spring:# redis 配置redis:# 地址host: 127.0.0.…...
Adobe After Effects AE v24.3.0 解锁版 (视频合成及视频特效制作)
Adobe系列软件安装目录 一、Adobe Photoshop PS 25.6.0 解锁版 (最流行的图像设计软件) 二、Adobe Media Encoder ME v24.3.0 解锁版 (视频和音频编码渲染工具) 三、Adobe Premiere Pro v24.3.0 解锁版 (领先的视频编辑软件) 四、Adobe After Effects AE v24.3.0 解锁版 (视…...
Qt---文件系统
一、基本文件操作 1. QFile对文件进行读和写 QFile file( path 文件路径) 读: file.open(打开方式) QlODevice::readOnly 全部读取->file.readAll(),按行读->file.readLine(),atend()->判断是否读到文件尾 …...
)
ruoyi-vue-pro 使用记录(2)
ruoyi-vue-pro 使用记录(2) 数据库商城商品模块数据表营销数据库交易数据库统计数据库 数据库 商城 参考官方文档 ruoyi-vue-pro yudao 项目商城 mall 模块启用及相关SQL脚本 商品模块(中心)以 product_ 作为前缀的表交易模块…...

centos7中如何全局搜索一下nginx的配置文件?
在CentOS 7中搜索Nginx的配置文件,你可以使用一些常用的命令行工具,比如find、grep等。这些工具可以帮助你在文件系统中查找文件,也可以用来查找Docker容器内部的文件,只要你知道如何访问容器的文件系统。 1. 搜索系统中的Nginx配…...

2024年5月10日有感复盘
2024年5月10日有感复盘 时间 今天是一个很美好的一天,原因是很平凡,读书很平凡,玩游戏很平凡,然后生活很平凡,未来可期,听歌很舒服,很喜欢一个人呆在图书馆的感觉,很喜欢发呆&…...

C++通过json文件配置参数
一、安装nlohmann json nlohmann json:安装_nlohmann安装-CSDN博客 依次执行下面指令: git clone https://gitee.com/cuihongxi/mov_from_github.gitcd json-developmkdir buildcd buildcmake ..makesudo make install 二、安装完成后使用 #include…...
idea连接远程仓库
git ->克隆。 url为远程仓库的地址,输入好后,选择项目存放目录,再点击克隆 点击新窗口打开。 切换到对应分支...

初始Django
初始Django 一、Django的历史 Django 是从真实世界的应用中成长起来的,它是由堪萨斯(Kansas)州 Lawrence 城中的一个网络开发小组编写的。它诞生于 2003 年秋天,那时 Lawrence Journal-World 报纸的程序员 Adrian Holovaty 和…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
