Day 46 139.单词拆分
单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
- 输入: s = “leetcode”, wordDict = [“leet”, “code”]
- 输出: true
- 解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。
示例 2:
- 输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
- 输出: true
- 解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。
- 注意你可以重复使用字典中的单词。
示例 3:
- 输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
- 输出: false
单词视为物品,字符串视为背包,又因为可以重复使用,所以是完全背包;
动规五部曲:
1.确定dp数组以及下标的含义
dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
2.确定递推公式
如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
3.dp数组如何初始化
从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]一定是true,否则递推下去后面都都是false了;
那么dp[0]有没有意义呢?dp[0]表示如果字符串为空的话,能否在字典中找到,很明显应该是false;
但题目中说了“给定一个非空字符串 s” 所以测试数据中不会出现i为0的情况,那么dp[0]怎样定义其实无所谓了;
下标非0的dp[i]初始化为false,只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词;
其实很多时候都会出现这种dp[0]赋值和意义不一致的情况,以递推公式为主;
4.确定遍历顺序
讨论两层for循环的前后顺序。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
而本题其实求的是排列数, 拿 s = “applepenapple”, wordDict = [“apple”, “pen”] 举例;
“apple”, “pen” 是物品,那么我们要求 物品的组合一定是 “apple” + “pen” + “apple” 才能组成 “applepenapple”;
“apple” + “apple” + “pen” 或者 “pen” + “apple” + “apple” 是不可以的,此处就是强调物品之间顺序;
所以一定是先遍历背包,再遍历物品;
for(int i = 1; i < s.size(); i++) {for(int j = 0; j < i; j++){string tempWord = s.substr(j, i - 1);if(dict.find(tempWord) != dict.end() && dp[j] == true){dp[i] = true;}}}
5.打印dp数组:
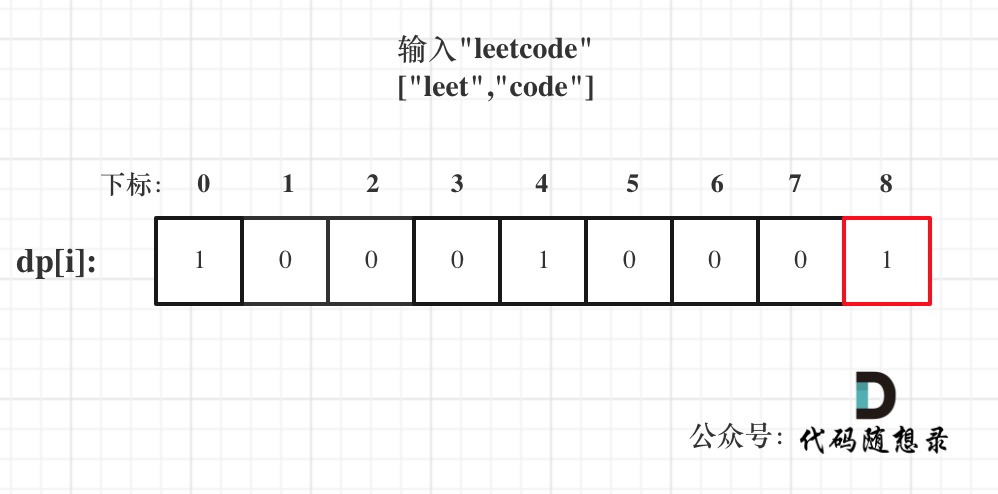
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordSet(wordDict.begin(), wordDict.end());//转化为unordered_set(即wordSet)的原因是为了提高查找效率vector<bool> dp(s.size() + 1, 0);dp[0] = true;for(int i = 1; i <= s.size(); i++) {for(int j = 0; j < i; j++){string tempWord = s.substr(j, i - j);if(wordSet.find(tempWord) != wordSet.end() && dp[j] == true){dp[i] = true;}}}return dp[s.size()];}
};
时间复杂度:O(n^3),因为substr返回子串的副本是O(n)的复杂度(这里的n是substring的长度)
空间复杂度:O(n)
多重背包
多重背包本质上可以视为01背包,因为数量仍然是有限个;
每件物品最多有M件可用,把M件摊开,其实01背包问题了;
但是不能完全按照01背包的代码来写,因为vector扩容是一件非常耗时的事情;
递推公式写成如下的形式,把每种商品遍历的个数放在01背包里面在遍历一遍,再递推,就解决了:
d p [ j ] = m a x ( d p [ j ] , d p [ j − k ∗ w e i g h t [ i ] ] + k ∗ v a l u e [ i ] ) dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]) dp[j]=max(dp[j],dp[j−k∗weight[i]]+k∗value[i]);
#include<iostream>
#include<vector>
using namespace std;
int main() {int bagWeight,n;cin >> bagWeight >> n;vector<int> weight(n, 0);vector<int> value(n, 0);vector<int> nums(n, 0);for (int i = 0; i < n; i++) cin >> weight[i];for (int i = 0; i < n; i++) cin >> value[i];for (int i = 0; i < n; i++) cin >> nums[i];vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < n; i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量// 以上为01背包,然后加一个遍历个数for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}}cout << dp[bagWeight] << endl;
}
时间复杂度:O(m × n × k),m:物品种类个数,n背包容量,k单类物品数量
背包问题总结
递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
动态规划:416.分割等和子集(opens new window)
动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
动态规划:494.目标和(opens new window)
动态规划:518. 零钱兑换 II(opens new window)
动态规划:377.组合总和Ⅳ(opens new window)
动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
动态规划:322.零钱兑换(opens new window)
动态规划:279.完全平方数
遍历顺序
对于01背包:
二维dp数组的两个for遍历的先后循序是可以颠倒的;
一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量;
对于完全背包:
因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的;
只要保证下标j之前的dp[j]都是经过计算的就可以了,颠倒是不会影响结果的;
但如果题目有所变动,不再是求纯完全背包问题:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
for循环先后循序一定是先遍历物品,再遍历背包容量;
对于完全背包:
因为dp[j] 是根据下标j之前所对应的dp[j]计算出来的;
只要保证下标j之前的dp[j]都是经过计算的就可以了,颠倒是不会影响结果的;
但如果题目有所变动,不再是求纯完全背包问题:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关文章:

Day 46 139.单词拆分
单词拆分 给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。 说明: 拆分时可以重复使用字典中的单词。 你可以假设字典中没有重复的单词。 示例 1: 输入: s “leet…...

streamlit报错:AxiosError: Request failed with status code 403
解决办法: 步骤一:创建config.toml vi ~/.streamlit/config.toml 步骤二:加入以下内容 [server] enableXsrfProtection false enableCORS false步骤三:重新启动你的streamlit网页...

java基础教学 |Java Stream API详解
Java Stream API 是Java 8引入的一个重要特性,它为集合对象提供了一种新的计算模型,使得开发者能够以声明性的方式处理数据集合。Stream API 不仅提高了代码的可读性和简洁性,还极大地优化了并行处理能力,让复杂的集合操作变得高效…...

0.0和0.00竟然不相等!!!BigDecimal别用错了比较方式
对于BigDecimal字段,可以使用compareTo()方法和equals()方法进行比较。但是要注意这两种方法的作用有所不同。一般都应该使用BigDecimal比较值,而不是使用经常用到的equals方法比较内容。 1.compareTo()方法 是用来比较两个BigDecimal对象的大小关系。…...

【多模态】30、Monkey | 支持大尺寸图像输入的多任务多模态大模型
文章目录 一、背景二、方法2.1 Enhancing Input Resolution2.2 Multi-level Description Generation2.3 Multi-task Training 三、效果3.1 Image Caption3.2 General VQA3.3 Scene Text-centric VQA3.4 Document-oriented VQA3.5 消融实验3.6 可视化 论文:Monkey : …...

PHP黑魔法之md5绕过
php本身是一种弱语言,这个特性决定了它的两个特点: 输入的参数都是当作字符串处理变量类型不需要声明,大部分时候都是通过函数进行类型转化php中的判断有两种: 松散比较:只需要值相同即可,类型不必相同,不通类型比较会先转化为同类型,比如全数字字符串和数字比较,会比…...
【适用全主题】WordPress原创插件:弹窗通知插件 支持内容自定义
内容目录 一、详细介绍二、效果展示1.部分代码2.效果图展示 三、学习资料下载 一、详细介绍 适用于所有WordPress主题的弹窗插件 一款WordPress原创插件:弹窗通知插件 支持内容自定义 二、效果展示 1.部分代码 代码如下(示例)࿱…...
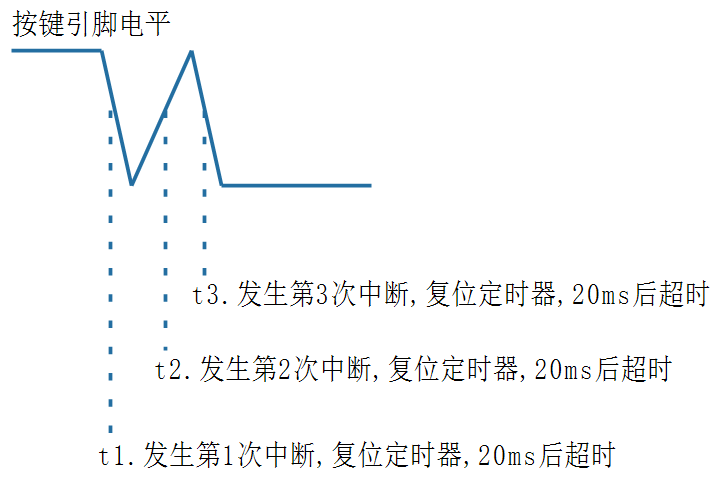
定时器的理论和使用
文章目录 一、定时器理论1.1定时器创建和使用 二、定时器实践2.1周期触发定时器2.2按键消抖 一、定时器理论 定时器是一种允许在特定时间间隔后或在将来的某个时间点调用回调函数的机制。对于需要周期性任务或延迟执行任务的嵌入式应用程序特别有用。 软件定时器: …...
【架构-17】通信系统架构设计理论
通信系统网络架构 1. 局域网网络架构 拓扑结构:星型、总线型、环型、树型。 网络架构:单核心架构(结构简单,地理范围受限)、双核心架构(网络拓扑结构可靠,投资较单核高)、环型架构…...

网络中的基本概念
网络初识 局域网:把若干个电脑组成在一起,通过路由器进行组网。 广域网:把局域网进一步的连接,构成更复杂的网络体系。 IP地址:区分主机。 端口号:区分主机上不同的程序。 协议:是一种约定&…...
手撸XXL-JOB(二)——定时任务管理
在上一节中,我们介绍了SpringBoot中关于定时任务的执行方式,以及ScheduledExecutorService接口提供的定时任务执行方法。假设我们现在要写类似XXL-JOB这样的任务调度平台,那么,对于任务的管理,是尤为重要的。接下来我们…...
DEV--C++小游戏(吃星星(0.2))
目录 吃星星(0.2) 简介 本次更新 分部代码 头文件(增) 命名空间变量(增) 副函数(新,增) 清屏函数 打印地图函数(增) 移动函数 选择颜色…...

Lua 协程池
协程池 在 使用 Lua 协程模拟 Golang 的 go defer 编程模式 中介绍了 Lua 协程的使用,模仿 golang 封装了下 还可以做进一步的优化 原来的 go 函数是这样实现的: function go(_co_task)local co coroutine.create(function(_co_wrap)_co_task(_co_w…...
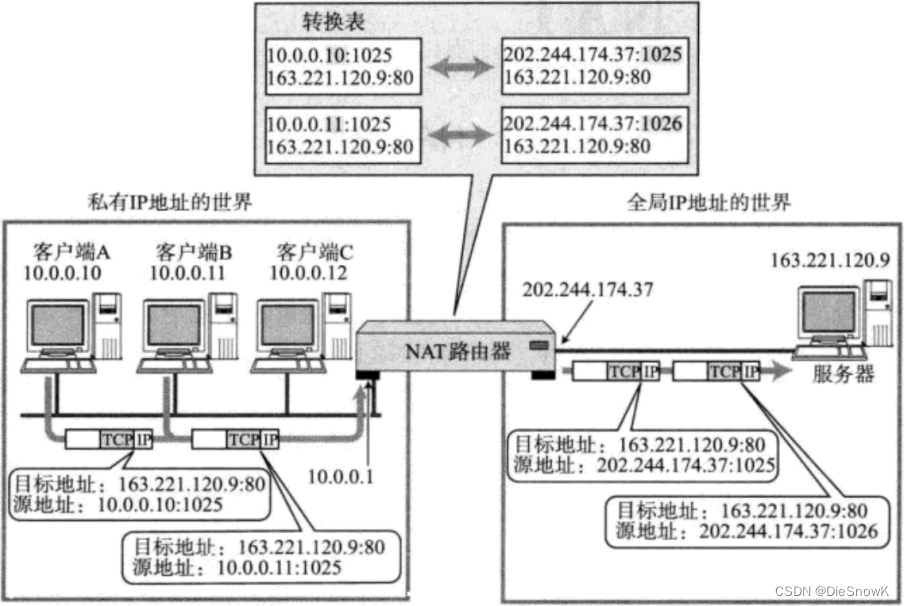
[Linux][网络][协议技术][DNS][ICMP][ping][traceroute][NAT]详细讲解
目录 1.DNS1.DNS背景2.域名简介 2.ICMP协议1.ICMP功能2.ICMP两类报文 3.ping命令4.traceroute5.NAT技术1.NAT技术背景2.NAT IP转换过程3.静态地址NAT && 动态地址NAT4.网络地址端口转换NAPT5.NAT技术的缺陷6.NAT和代理服务器 6.总结1.数据链路层2.网络层3.传输层4.应用…...
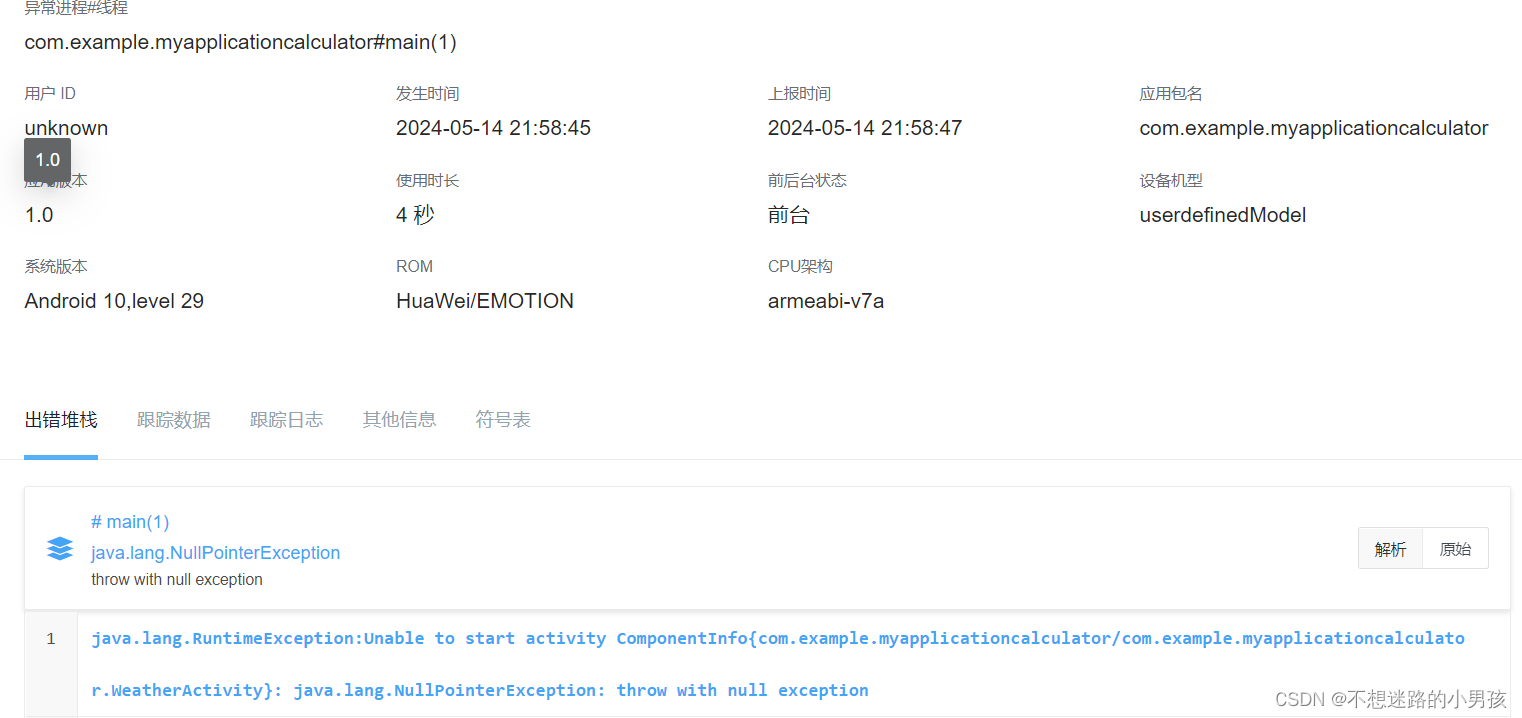
Android 集成Bugly完成线上的异常Exception收集及处理
文章目录 (一)添加产品APP(二)集成SDK(三)参数配置权限混淆 (四)初始化 (一)添加产品APP 一)在个人头像 -> 我的头像 -> 新建产品 二&…...

Redis——Redis的数据库结构、删除策略及淘汰策略
Redis是一个高性能的key-value存储系统,它支持多种数据结构,并提供了丰富的删除策略和淘汰策略。以下是关于Redis的数据库结构、删除策略及淘汰策略的详细介绍: Redis的数据库结构 Redis是一个key-value数据库,数据存储是以一个…...

【Vue3笔记03】Vue3项目工程中使用vue-router路由
这篇文章,主要介绍Vue3项目工程中如何使用vue-router路由。 目录 一、vue-router路由 1.1、下载vue-router路由 1.2、创建router.js文件 1.3、main.js配置路由...
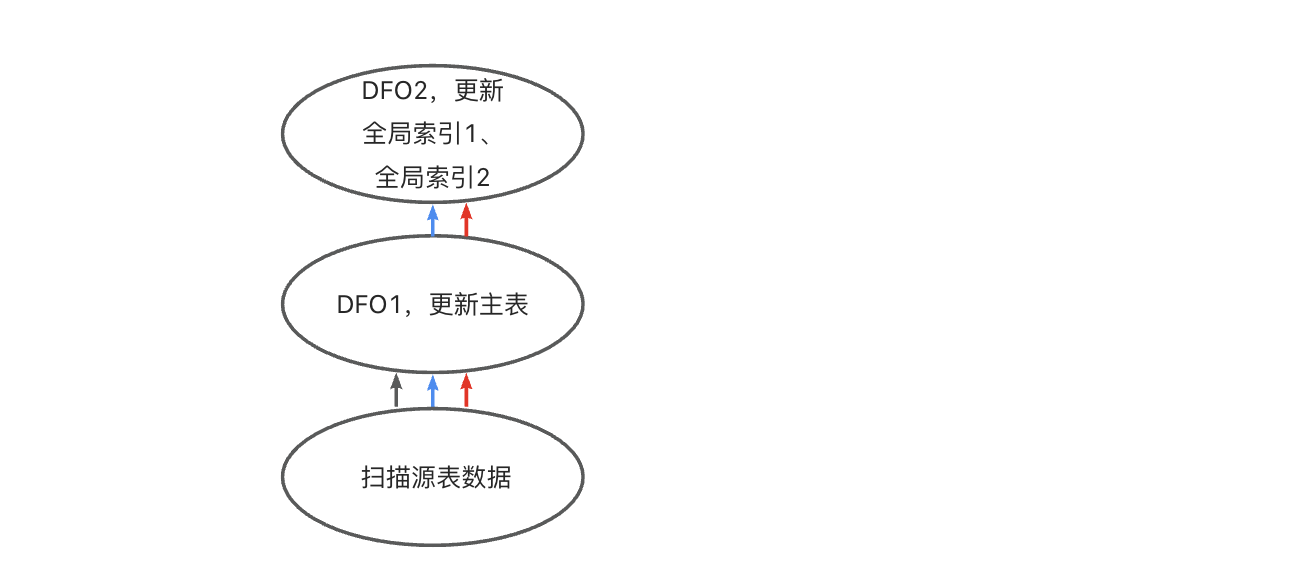
并行执行的4种类别——《OceanBase 并行执行》系列 4
OceanBase 支持多种类型语句的并行执行。在本篇博客中,我们将根据并行执行的不同类别,分别详细阐述:并行查询、并行数据操作语言(DML)、并行数据定义语言(DDL)以及并行 LOAD DATA 。 《并行执行…...

函数练习.
1.打印乘法口诀表 口诀表的行数和列数自己指定如:输入9,输出99口诀表,输出12,输出1212的乘法口诀表。 multiplication(int index) { if (index 9) { int i 0; for (i 1; i < 10; i) { int j 0; for (j 1; j &…...

Git 分支命令操作详解
目录 1、分支的特点 2、分支常用操作 3、分支的使用 3.1、查看分支 3.2、创建分支 3.3、修改分支 3.4、切换分支 3.5、合并分支 3.6、产生冲突 3.7、解决冲突 3.8、创建分支和切换分支说明 1、分支的特点 同时并行推进多个功能开发,提高开发效率。各个分…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
