JS算法-十大排序算法(上)
思想小剧场
如果我的相对论被证明是正确的,德国人就会说我是德国人,法国人会说我是一个世界公民;如果我的相对论被否定了,法国佬就会骂我是德国鬼子,而德国人就会把我归为犹太人。—爱因斯坦
以下案例都是升序
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
冒泡排序
一个一个数进行处理,第i个数,需要与后续的len-i-1个数进行逐个比较
// 1、冒泡排序
const bubbleSort = (arr) => {const len = arr.length;for (let i = 0; i < len - 1; i++) {for (let j = 0; j < len - i - 1; j++) { // 相邻元素两两比较if (arr[j] > arr[j+1]) {[arr[j], arr[j+1]] = [arr[j+1], arr[j]]; // 元素交换}}}return arr;
}
console.log("冒泡排序 => ", bubbleSort(arr))
快速排序(冒泡)
通过选定一个数字作为比较值,将要排序的其他数字,分为 >比较值 和 <比较值 两个部分。并不断重复这个步骤,直到只剩要排序的数字只有本身,则排序完成
// 2、快速排序 - 分治法
const quickSort = (arr) => {const sort = (arr, low, high) => {if (low >= high) {return;}let i = low;let j = highconst x = arr[i]; // 取出比较值while (i < j) {// 从数组尾部,找出比x小的数,放到左边while (arr[j] >= x && i < j) {j--;}// 将空出的位置,填入当前值,下标j位置空出if (i < j) {arr[i] = arr[j];i++;}// 从数组头部,找出比x大的数字while (arr[i] <= x && i < j) {i++;}// 将数字填入下标j中,下标i位置突出if (i < j) {arr[j] = arr[i];j--;}// 一直循环到左右指针i、j相遇// 相遇时,i==j,所以下标i位置空出的}arr[i] = x; // 将空出的位置,填入缓存的数字x,一轮排序完成// 分别对剩下的两个区间进行递归排序sort(arr, low, i - 1);sort(arr, i + 1, high);}sort(arr, 0, arr.length - 1); return arr;}console.log("快速排序 => ", quickSort(arr))
希尔排序
是一种插入排序的算法,是对简单的插入排序进行改进后,更高效的版本。
特点是利用增量,将数组分为一组组子序列,然后对子序列进行插入排序。
由于增量是从大到小,逐次递减,所以也称为缩小增量排序。
注意:插入排序时,并不是一个分组内的数字一次性用插入排序完成,而是每个分组交叉进行
执行插入时,使用交换法
// 3.1、希尔排序 - 执行插入时,使用交换法
const shellSort = (arr) => {// 分组规则 gap 递减for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) {for (let i = gap; i < arr.length; i++) {let j = i;// 分组内数据,执行插入排序// 当下标大的数字,小于 下标小的数字,进行交互// 分组内的数字,并不是一次性比较完,需要i逐步递增,包括下个分组内的数字while (j - gap >= 0 && arr[j] < arr[j - gap]) {[arr[j], arr[j - gap]] = [arr[j - gap], arr[j]];j = j - gap;}}}return arr;
}
console.log("希尔排序(交换法) => ", shellSort(arr))
执行插入时,使用移动法
// 3.2、希尔排序 - 执行插入时,使用移动法
const shellSort2 = (arr) => {// 分组规则 gap 递减for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) {for (let i = gap; i < arr.length; i++) {let j = i;// 缓存数字,空出位置const x = arr[j];// 分组内数据,执行插入排序// 当下标大的数字,小于 下标小的数字,进行交互// 分组内的数字,并不是一次性比较完,需要i逐步递增,包括下个分组内的数字while (j - gap >= 0 && x < arr[j - gap]) {arr[j] = arr[j - gap]; // 将符合条件的数字,填入空出的位置j = j - gap;}arr[j] = x; // 将缓存的数字,填入空出的位置}}return arr;
}
console.log("希尔排序(移动法) => ", shellSort2(arr))
选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
// 4、选择排序
const selectionSort = (arr) => {for (let i = 0, len = arr.length; i < len - 1; i++) {for (let j = i + 1; j < len; j++) {if (arr[i] > arr[j]) {[arr[i], arr[j]] = [arr[j], arr[i]]; // 元素交换}}}return arr;
}
console.log("选择排序 => ", selectionSort(arr))
归并排序(分治)
利用分治思想,将大的数组,分解为小数组,直至单个元素。然后,使用选择排序的方式,对拆分的小数组,进行回溯,并有序合并,直至合并为一个大数组。
// 5、归并排序 - 分治
const mergeSort = (arr) => {// 合并两个有序数组const mergeSort = (leftArr, rightArr) => {let left = 0;let right = 0;const temp = [];// 使用双指针,对两个数组进行扫描while (left < leftArr.length && right < rightArr.length) {if (leftArr[left] < rightArr[right]) {temp.push(leftArr[left++]);} else {temp.push(rightArr[right++]);}}// 合并剩下的内容if (left < leftArr.length) {while (left < leftArr.length) {temp.push(leftArr[left++]);}}if (right < rightArr.length) {while (right < rightArr.length) {temp.push(rightArr[right++]);}}return temp;}// sort 方法,进行递归const sort = (arr, left, right) => {// 当 left !== right 时,证明还没拆分到最小元素if (left < right) {// 取中间值,拆分为两个小的数组const mid = Math.floor((left + right) / 2);// 递归拆分左边数组const leftArr = sort(arr, left, mid);// 递归拆分右边数组 const rightArr = sort(arr, mid + 1, right);// 合并两个数组return mergeSort(leftArr, rightArr)}// left === right 时,已经是最小元素,直接返回即可return left >= 0 ? [arr[left]] : []}return sort(arr, 0, arr.length - 1);
}
console.log("归并排序 => ", mergeSort(arr))
相关文章:
)
JS算法-十大排序算法(上)
思想小剧场 如果我的相对论被证明是正确的,德国人就会说我是德国人,法国人会说我是一个世界公民;如果我的相对论被否定了,法国佬就会骂我是德国鬼子,而德国人就会把我归为犹太人。—爱因斯坦 以下案例都是升序 const a…...
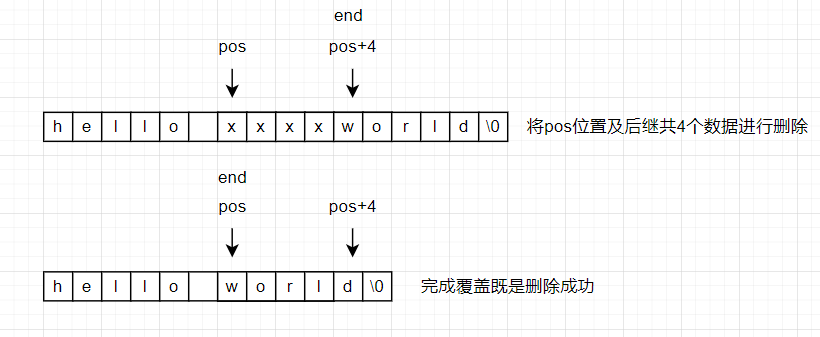
c++编程(11)——string类的模拟实现
欢迎来到博主的专栏——c编程 博主ID:代码小豪 文章目录 前言string类的模拟实现string的成员对象构造、赋值、析构访问成员对象的接口访问字符串中的元素迭代器对字符序列的插入、删除元素操作mystring类的相关操作 mystring类的所有模拟实现以及测试案例 前言 本…...
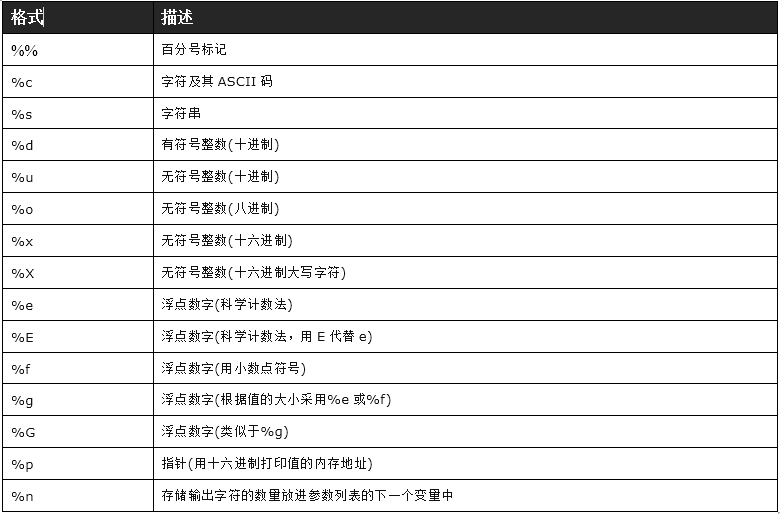
Python从0到POC编写--函数
数学函数: 1. len len() 函数返回对象(字符、列表、元组等)长度或项目个数, 例如: str "python" len(str)2. range range() 函数返回的是一个可迭代对象(类型是对象),…...
【教程】Linux/Jetson 安装X11VNC同步屏幕内容
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,请不吝给个[点赞、收藏、关注]哦~ 目录 背景说明 实际效果 安装步骤 安装 x11vnc 配置 x11vnc 配置 x11vnc 作为系统服务 使用 VNC 客户端连接 背景说明 通常vnc-server是单…...
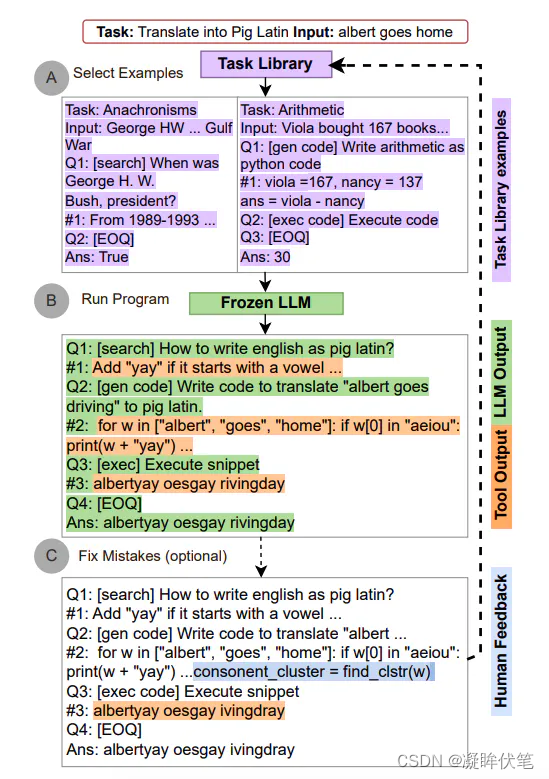
【LLM第五篇】名词解释:prompt
1.是什么 提示工程(Prompt Engineering)是一门较新的学科,关注提示词开发和优化,帮助用户将大语言模型(Large Language Model, LLM)用于各场景和研究领域。 掌握了提示工程相关技能将有助于用户更好地了解…...
k8s v1.20二进制部署 部署 CNI 网络组件 部署 Calico
一、部署 flannel 1.1.K8S 中 Pod 网络通信 ●Pod 内容器与容器之间的通信 在同一个 Pod 内的容器(Pod 内的容器是不会跨宿主机的)共享同一个网络命名空间,相当于它们在同一台机器上一样,可以用 localhost 地址访问彼此的端口。…...
在React中利用Postman测试代码获取数据
文章目录 概要名词解释1、Postman2、axios 使用Postman测试API在React中获取并展示数据小结 概要 在Web开发中,通过API获取数据是一项常见任务。Postman是一个功能强大的工具,可以帮助开发者测试API,并查看API的响应数据。在本篇博客中&…...
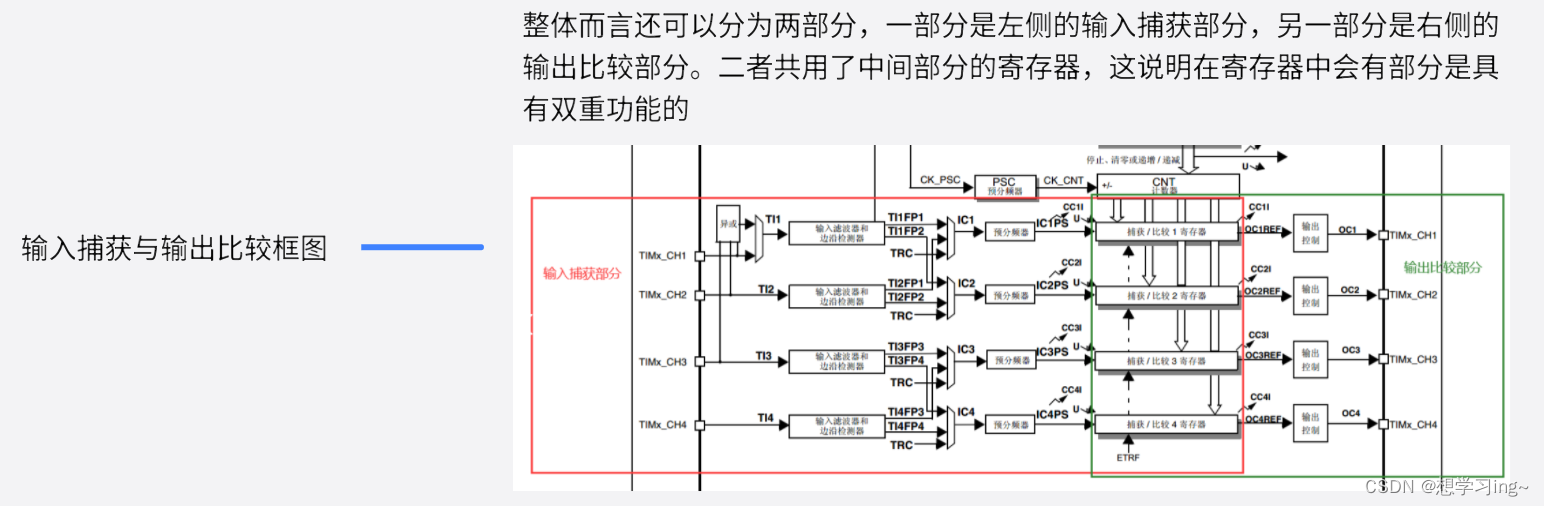
嵌入式学习-通用定时器
简介 框图介绍 时钟选择 计数器部分 输入捕获和输出比较框图 嵌入式学习全文参考(小向是个der)做笔记:https://blog.csdn.net/qq_41954556/article/details/129735708...

培训行业有哪些ai工具?
培训行业利用人工智能(AI)工具的方式多种多样,其中一些常见的工具包括: 1. **经AI深度学习的OCR软件**:OCR能给培训行业带来很大的便利,能大大提高工作效率和降低文字录入的成本,但一般的OCR工具…...
7.STL中string的一些超常用函数 (附习题)
目录 1.find 2.atoi 3.to_string 4.getline 【leetcode 习题】 387.字符串中的第一个唯一字符 125. 验证回文串 1.find 1.查找第一次出现的目标字符串:说明:如果查找成功则输出查找到的第一个位置,否则返回-1; s1.find(s2…...

GPT搜索鸽了!改升级GPT-4
最近OpenAI太反常,消息一会一变,直让人摸不着头脑。 奥特曼最新宣布:5月13日开发布会,不是GPT-5,也不是盛传的GPT搜索引擎,改成对ChatGP和GPT-4的升级~ 消息一出,大伙儿都蒙了。 之…...

数字绘画教学实训解决方案
一、建设背景 1.1政策背景 教育信息化政策推动:近年来,随着教育信息化政策的不断推动,各级教育部门纷纷出台相关政策,鼓励和支持教育信息化的发展。数字绘画作为现代艺术教育的重要组成部分,其教学实训解决方案的建设…...

C#之如何判断数据类型
一、GetType方法 a.GetType():获取当前变量的类型对象 string str "Hello World";Console.WriteLine(str.GetType()); 结果: 二、typeof方法 typeof(Int):获取的是Int类型的类型对象 int num 10;Console.WriteLine(num.GetType() typeof(i…...
)
算法学习笔记(Tarjan)
本文介绍 T a r j a n Tarjan Tarjan求强联通分量、找割点和割边、找环。 Tarjan求强联通分量 例题:【模板】有向图缩点 题目描述 给定一个 n n n点 m m m边的有向图(保证不存在重边与自环,但不保证连通),请你求出…...
一台linux通过另一台linux访问互联网-TinyProxy
参考: https://blog.csdn.net/weixin_41831919/article/details/113061317https://www.yuncongz.com/archives/1.htmlhttps://blog.csdn.net/aoc68397/article/details/101893369 环境:ubuntu 18.04 机器1: IP 219.216.65.252 (可以访问外网) 机器2: IP…...

探索数据结构:堆的具体实现与应用
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 堆的概念 堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个…...
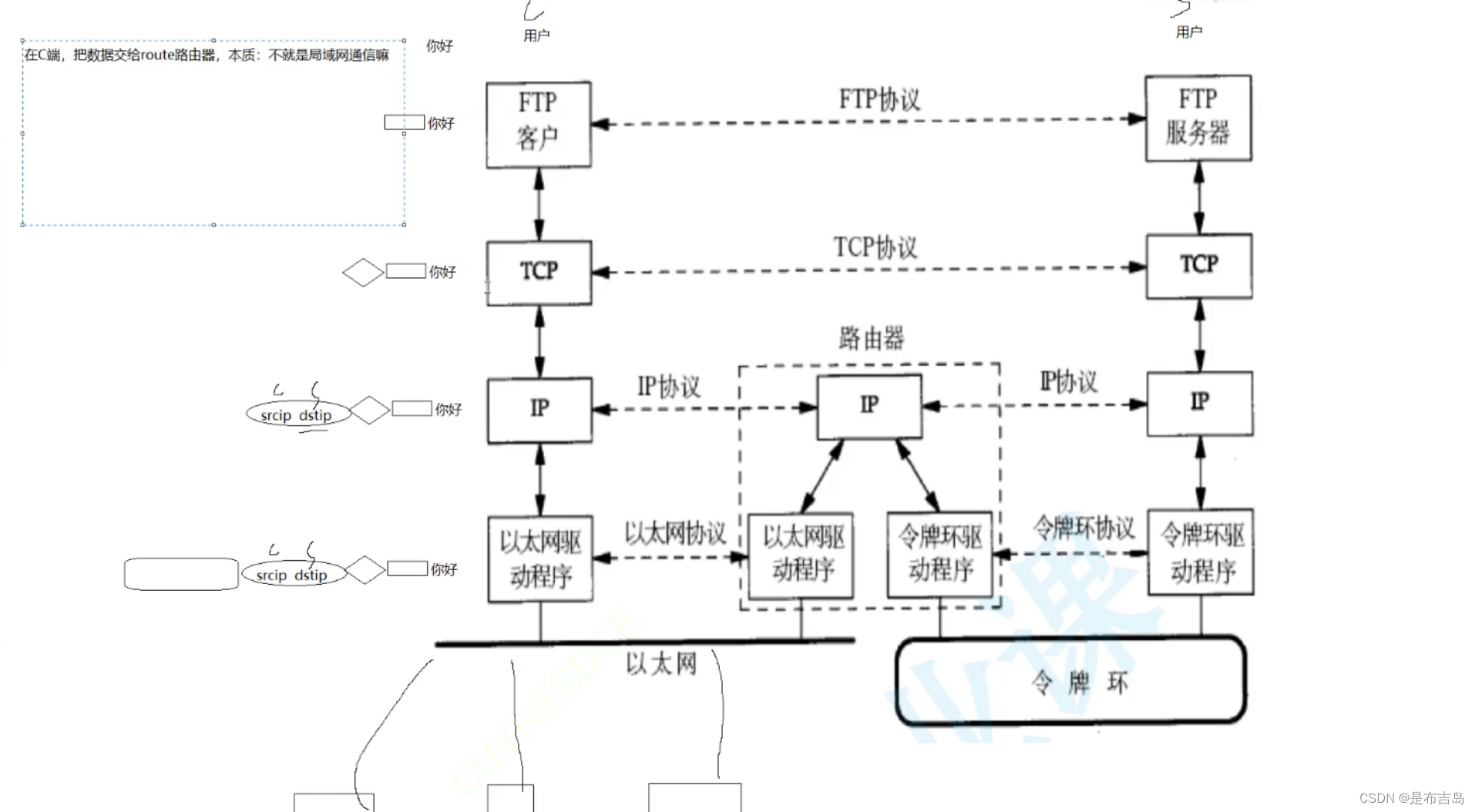
网络2--MAC地址,IP地址的理解
引入: 每一张主机都会有一张网卡,每一张网卡都有一个48bit位的序列号 当我们的热点被连上,你查看时,就会出现MAC地址,IP地址 那么他们两个是什么呢??? MAC地址 在同一个局域网中…...

类型的转换
首先我们要了解java中的数据类型转换是指将一种数据类型转换成另一种数据类型的过程。 什么时候会用到?我觉得两种情况会用到 等号左右两边类型不一致(一般发生在赋值时)不同类型的数据参与运算(一般发生在计算时) 转…...

memset函数
让我们先看两个代码 memset(dp, 0x3f, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; memset(dp, 127, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; 代码结果如下: 现在我们来分…...

Java面向对象——多态
即同一个方法可以根据发送对象的不同而采用多种不同的行为方式。 一个对象的实际类型是确定的,但可以指向对象的引用的类型有很多(父类,有关系的类)。 多态存在的条件: 1. 有继承关系; 2. 子类重写父类…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
