算法学习笔记(Tarjan)
本文介绍 T a r j a n Tarjan Tarjan求强联通分量、找割点和割边、找环。
Tarjan求强联通分量
例题:【模板】有向图缩点
题目描述
给定一个 n n n点 m m m边的有向图(保证不存在重边与自环,但不保证连通),请你求出其中所有“大小大于 1 1 1”的强联通分量的大小,如果不存在则输出 − 1 −1 −1。
将所有强联通分量大小按从小到大顺序输出。
输入描述
第一行两个整数 n , m n,m n,m。 ( 1 ≤ n , m ≤ 2 × 1 0 5 ) (1 \leq n,m \leq 2 \times 10^5) (1≤n,m≤2×105)
接下来 m m m行,每行一条边 ( x , y ) (x,y) (x,y),表示存在一条由点 x x x到点 y y y的边。 ( 1 ≤ x , y ≤ n ) (1≤x,y≤n) (1≤x,y≤n)
输出描述
一行从小到大输出所有“大小大于 1 1 1”的强联通分量的大小,若不存在则输出 − 1 −1 −1。
输入样例1
4 4
1 2
2 3
3 1
1 4
输出样例1
3
强连通:在有向图 G G G中,如果两个点 u u u和 v v v是互相可达的,即从 u u u出发可以到达 v v v,从 v v v出发可以到达 u u u,则称 u u u和 v v v是强连通的。如果 G G G中任意两个点都是互相可达的,称 G G G是强连通图。
强连通分量(SCC):如果一个有向图 G G G不是强连通图,那么可以把它分成多个子图,其中每个子图的内部是强连通的,而且这些子图已经扩展到最大,不能与子图外的任意点强连通,称这样的一个“极大强连通”子图是 G G G的一个强连通分量。
接下来说明一个定理: S C C SCC SCC,从其中任意一个点出发,都至少有一条路径能绕回到自己。
明白这点之后,解释一下 T a r j a n Tarjan Tarjan求强连通分量的流程。
首先对于每一个节点,都有两个量: d f n dfn dfn和 l o w low low, d f n dfn dfn表示该节点的 d f s dfs dfs序, l o w low low则表示该节点能返回到的最远祖先(对图跑 d f s dfs dfs生成搜索树,树上节点有祖先),初始时 l o w low low就等于自己的 d f s dfs dfs序,在之后更新的时候,有两种情况可以更新 l o w low low的值。一种是一个节点有一条有向边指向自己在搜索树上的祖先时,比较自己的 l o w low low和被访问到的祖先的 d f n dfn dfn,将自己的 l o w low low更新为两者中的最小值。还有一种情况就是 d f s dfs dfs回溯时,比较自己的 l o w low low和儿子的 l o w low low,将自己的 l o w low low更新为两者中的较小值。更新完回来之后,回到 d f n = l o w dfn = low dfn=low的点,作为强连通分量的根。将刚刚修改过 l o w low low值的点收拢,作为一个强连通分量。
特殊的,如果一个点有一条有向边指向了一个强连通分量,那么我们不应该去更新它的 l o w low low。
为了区别这种情况,我们会使用栈来分离不同的 S C C SCC SCC,每访问一个点就将点丢入栈中,而每找出一个 S C C SCC SCC,则将这个 S C C SCC SCC中的所有点从栈中弹出。之后有边指向这个 S C C SCC SCC则不再理会(指向的点不在栈中说明已经属于一个 S C C SCC SCC)。
时间复杂度为: O ( n + m ) O(n + m) O(n+m)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 9, T = 20;vector<int> g[N];int dfn[N], low[N], stk[N], top, idx;
int tot, cnt[N];
bitset<N> ins;//tarjan的本质是dfs
void tarjan(int x)
{//1.初始化dfn和lowdfn[x] = low[x] = ++ idx;//2.入栈并标记stk[++ top] = x;ins[x] = true;//3.遍历所有儿子for(const auto &y : g[x]){//判断是否是回点if(!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if(ins[y]) low[x] = min(low[x], dfn[y]);}//4.收拢if(low[x] == dfn[x]){//新开一个颜色tot ++;while(stk[top + 1] != x){//计数cnt[tot] ++;//取消标记ins[stk[top --]] = false;}}
}void solve()
{int n, m;cin >> n >> m;for(int i = 1;i <= m; ++ i){int x, y;cin >> x >> y;g[x].push_back(y);}for(int i = 1;i <= n; ++ i)if(!dfn[i])tarjan(i);vector<int> v;for(int i = 1;i <= tot; ++ i)if(cnt[i] > 1)v.push_back(cnt[i]);if(v.size()){sort(v.begin(), v.end());for(const auto &i : v)cout << i << ' ';}else cout << -1 << '\n';
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1;while(_ --)solve();return 0;
}
Tarjan求割点和割边
例题:【模板】无向图求割点、割边
题目描述
给一个 n n n点 m m m边的无向图(无重边与自环),请求出图中所有割点和割边的数量。
输入描述
第一行两个整数 n , m n,m n,m。 ( 1 ≤ n , m ≤ 2 × 1 0 5 ) (1 \leq n,m \leq 2 \times 10^5) (1≤n,m≤2×105)
接下来 m m m行,每行两个整数 x , y x,y x,y表示一条 x x x与 y y y之间的双向边。 ( 1 ≤ x , y ≤ n ) (1 \leq x,y \leq n) (1≤x,y≤n)。
输出描述
一行两个整数,表示割点和割边的数量。
输入样例1
4 4
1 2
3 2
2 4
1 3
输出样例1
1 1
解释
割点为 2 2 2,割边为 2 − 4 2−4 2−4。
割点和割边:无向图中所有能互通的点组成了一个“连通分量”。在一个连通分量中有一些关键的的点,如果删除它们,会把这个连通分量断开分为两个或更多,这种点称为割点。同样的,如果在一个连通分量中删除一条边,把这个连通分量分成了两个,这条边称为割边。
对于一个点:分两种情况,一是不作为搜索树的根的节点,只要在由这个节点的儿子中,有一个节点不连通到该节点的祖先( l o w [ y ] ≥ d f n [ x ] low[y] \geq dfn[x] low[y]≥dfn[x]),那么这个节点是割点(由该节点作为分界线,分割了它的儿子做根的子树和它的父亲)。二是作为搜索树的根的节点,需要两个儿子不连通到该节点( l o w [ y ] ≥ d f n [ x ] low[y] \geq dfn[x] low[y]≥dfn[x]),那么这个节点是割点(删除这个根,两棵子树就被分离开来了)。
而对于一条边,只要后边的点回不到前边的点( l o w [ y ] ≥ d f n [ x ] low[y] \geq dfn[x] low[y]≥dfn[x]),那么这个点就是割边。
那么计算割点割边只需要看是否满足上述条件就行。
#include <bits/stdc++.h>
#include <assert.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 9;vector<int> g[N];int dfn[N], low[N], idx, cut, es;void tarjan1(int x, int fa)
{dfn[x] = low[x] = ++ idx;int child = 0;for(const auto &y: g[x]){//1.不走父亲if(y == fa)continue;//2.判断是否是搜索树的儿子if(!dfn[y]){tarjan1(y, x);low[x] = min(low[x], low[y]);child += (low[y] >= dfn[x]);}else low[x] = min(low[x], dfn[y]);}if((!fa && child >= 2) || (fa && child >= 1))cut ++;
}void tarjan2(int x, int fa)
{dfn[x] = low[x] = ++ idx;for(const auto &y : g[x]){if(y == fa)continue;//如果y没被走过,就往下走if(!dfn[y]){//此时y是x在搜索树中的儿子tarjan2(y, x);low[x] = min(low[x], low[y]);//如果y回不到自身以及父亲树上if(low[y] > dfn[x])es ++;}else low[x] = min(low[x], dfn[y]);}
}set<pair<int, int> > st;void solve()
{int n, m;cin >> n >> m;for(int i = 1;i <= m; ++ i){int x, y;cin >> x >> y;g[x].push_back(y);g[y].push_back(x);}for(int i = 1;i <= n; ++ i)if(!dfn[i])tarjan1(i, 0);for(int i = 1;i <= n; ++ i)dfn[i] = low[i] = 0;idx = 0;for(int i = 1;i <= n; ++ i)if(!dfn[i])tarjan2(i, 0);cout << cut << ' ' << es << '\n';
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1;while(_ --)solve();return 0;
}
Tarjan找环
例题:【模板】Tarjan找环
题目描述
给定一个 n n n点 n n n边的无向连通图(不含重边与自环),请你求出图中环的大小。
可以证明图中存在且仅存在一个环。
输入描述
第一行一个整数表示测试样例数量 T T T。 ( 1 ≤ T ≤ 1000 ) (1 \leq T \leq 1000) (1≤T≤1000)
对于每组测试样例,第一行一个整数 n n n。 ( 1 ≤ n ≤ 2 × 1 0 5 ) (1 \leq n \leq 2 \times 10^5) (1≤n≤2×105)
接下来 n n n行,每行一条无向边 u , v u,v u,v。 ( 1 ≤ u , v ≤ n ) (1 \leq u,v \leq n) (1≤u,v≤n)
输出描述
对于每组测试样例,输出一个整数表示环的大小。
输入样例1
2
5
1 2
1 3
2 3
3 4
4 5
4
1 2
2 3
3 4
1 4
输出样例1
3
4
对于找环,找出一个强连通分量就是环。因为 n n n点 n n n边,一定存在且仅存在一个环(一棵树 n − 1 n - 1 n−1条边,多连一条边必定生成一个环)。于是只要在找强连通分量的代码上稍加修改就行。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 9;vector<int> g[N];int dfn[N], low[N], idx, ans;
int stk[N], top;
bitset<N> ins;void tarjan(int x, int fa)
{dfn[x] = low[x] = ++ idx;stk[++ top] = x;ins[x] = true;for(const auto &y : g[x]){if(y == fa)continue;if(!dfn[y]){tarjan(y, x);low[x] = min(low[x], low[y]);}else if(ins[x])low[x] = min(low[x], dfn[y]);}if(low[x] == dfn[x]){int cnt = 0;while(stk[top + 1] != x){cnt ++;ins[stk[top --]] = false;}if(cnt > 1){ans = cnt;return;}}}void solve()
{int n;cin >> n;for(int i = 1;i <= n; ++ i){g[i].clear();stk[i] = dfn[i] = low[i] = 0;ins[i] = false;}stk[n + 1] = 0;ans = idx = top = 0;for(int i = 1;i <= n; ++ i){int x, y;cin >> x >> y;g[x].push_back(y);g[y].push_back(x);}tarjan(1, 0);cout << ans << '\n';
}
int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin >> _;while(_ --)solve();return 0;
}
( T a r j a n Tarjan Tarjan找环应该只使用于 n n n点 n n n边的情况?)
相关文章:
)
算法学习笔记(Tarjan)
本文介绍 T a r j a n Tarjan Tarjan求强联通分量、找割点和割边、找环。 Tarjan求强联通分量 例题:【模板】有向图缩点 题目描述 给定一个 n n n点 m m m边的有向图(保证不存在重边与自环,但不保证连通),请你求出…...
一台linux通过另一台linux访问互联网-TinyProxy
参考: https://blog.csdn.net/weixin_41831919/article/details/113061317https://www.yuncongz.com/archives/1.htmlhttps://blog.csdn.net/aoc68397/article/details/101893369 环境:ubuntu 18.04 机器1: IP 219.216.65.252 (可以访问外网) 机器2: IP…...

探索数据结构:堆的具体实现与应用
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 堆的概念 堆(Heap)是计算机科学中一类特殊的数据结构。堆通常是一个…...
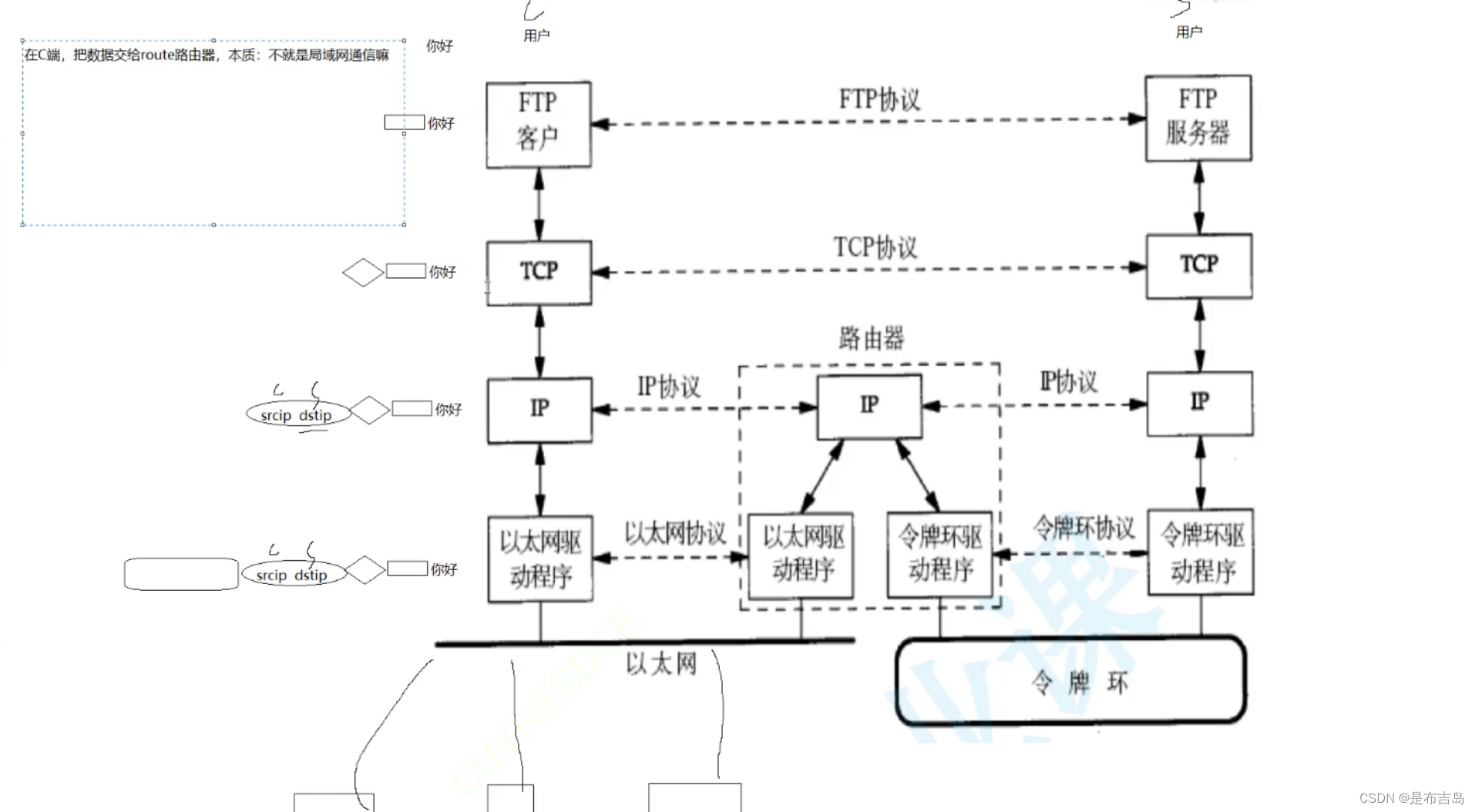
网络2--MAC地址,IP地址的理解
引入: 每一张主机都会有一张网卡,每一张网卡都有一个48bit位的序列号 当我们的热点被连上,你查看时,就会出现MAC地址,IP地址 那么他们两个是什么呢??? MAC地址 在同一个局域网中…...

类型的转换
首先我们要了解java中的数据类型转换是指将一种数据类型转换成另一种数据类型的过程。 什么时候会用到?我觉得两种情况会用到 等号左右两边类型不一致(一般发生在赋值时)不同类型的数据参与运算(一般发生在计算时) 转…...

memset函数
让我们先看两个代码 memset(dp, 0x3f, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; memset(dp, 127, sizeof(dp)); for (int i 0; i < 5; i)cout << dp[i] << " "; 代码结果如下: 现在我们来分…...

Java面向对象——多态
即同一个方法可以根据发送对象的不同而采用多种不同的行为方式。 一个对象的实际类型是确定的,但可以指向对象的引用的类型有很多(父类,有关系的类)。 多态存在的条件: 1. 有继承关系; 2. 子类重写父类…...
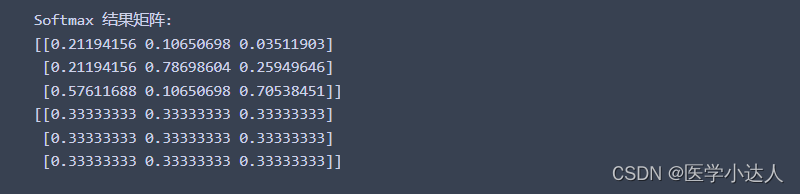
python 对矩阵与矩阵之间对应位置的元素,做softmax操作,代码实战
1.对矩阵中对应位置的元素,做softmax 对于一个向量,softmax函数会对其中每一个元素进行指数运算,然后除以所有元素指数和的结果。当将其应用到多个矩阵的相应位置上时,我们实际上是在对每个位置的一组数(从各个矩阵的同…...

Angular前端项目在Apache httpd服务器上的部署
Apache Httpd和Tomcat主要区别:Tomcat是一个Java Servlet容器,用于运行Java Servlet和JavaServer Pages(JSP),而Apache HTTP服务器是一个通用的Web服务器,用于提供静态和动态内容。 Apache httpd安装&#…...

Oracle 更改数据文件位置的几种常用方式
Oracle 更改数据文件位置的几种常用方式 A.归档模式下 1、offline 表空间:alter tablespace tablespace_name offline; 2、复制数据文件到新的目录; 3、rename 修改表空间,并修改控制文件; 4、online 表空间…...

【opencv】图像畸变校正
接上篇文章:【鱼眼+普通相机】相机标定 附代码: 方法一: 使用cv2.undistort """Create May 11, 2024author Wang Jiajun """import cv2 import numpy as npdef correct(img,camera_fileE:/cali…...

Charger之二输入电压动态电源原理(VIN-DPM)
主要内容 Charger的VIN-DPM 前篇内容:电池管理IC(Charger)了解一下? 领资料:点下方↓名片关注回复:粉丝群 正文 一、 VIN-DPM概念 VIN-DPM是指输入电压动态电源管理(Input voltage dynamic…...
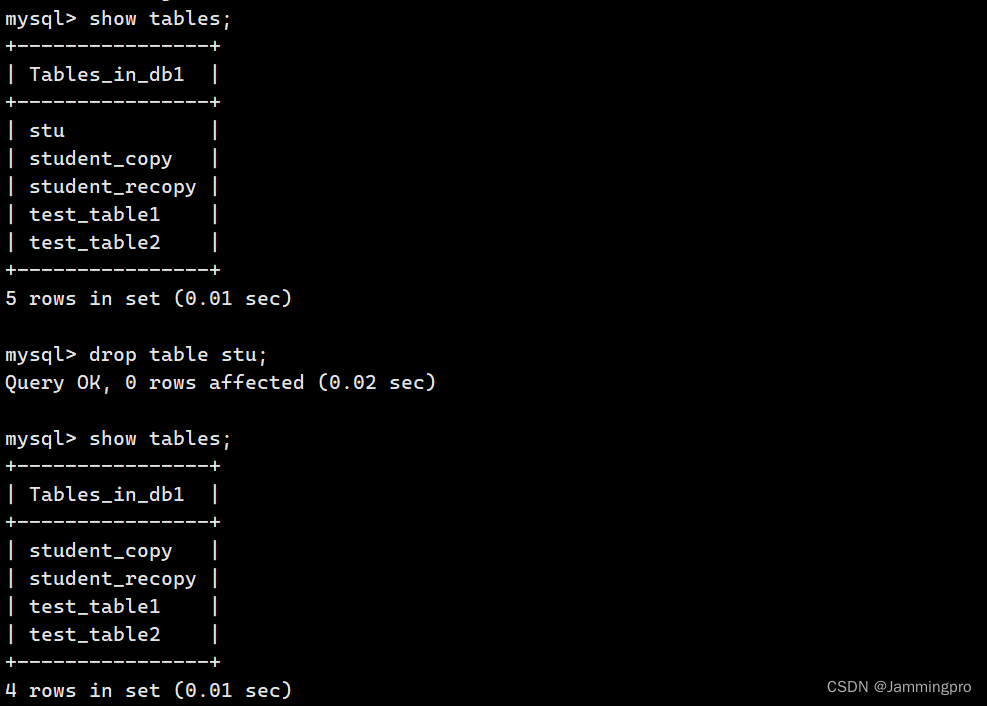
【半夜学习MySQL】表结构的操作(含表的创建、修改、删除操作,及如何查看表结构)
🏠关于专栏:半夜学习MySQL专栏用于记录MySQL数据相关内容。 🎯每天努力一点点,技术变化看得见 文章目录 创建表查看表结构修改表删除表 创建表 语法: create table table_name(field1 datatype,field2 datatype,fiel…...
曲线救国:window 安装 docker
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益: 了解大厂经验拥有和大厂相匹配的技术等 希望看什么,评论或者私信告诉我! 文章目录 一…...

番外篇 | 利用PyQt5+YOLOv5来搭建目标检测系统(附可视化界面+功能介绍+源代码)
前言:Hello大家好,我是小哥谈。PyQt5是一个Python绑定的Qt库,是用于创建图形用户界面(GUI)和其他应用程序组件的工具包。PyQt5提供了许多GUI元素,如按钮、文本框、标签等,也提供了许多Qt的功能,如网络、数据库、XML等。通过PyQt5可以在Python中使用Qt的丰富功能和强大的工…...
Pascal Content数据集
如果您想使用Pascal Context数据集,请安装Detail,然后运行以下命令将注释转换为正确的格式。 1.安装Detail 进入项目终端 #即 这是在我自己的项目下直接进行克隆操作: git clone https://github.com/zhanghang1989/detail-api.git $PASCAL…...
【Unity】使用Resources.LoadAll读取文件的顺序问题
最近在做客户的一个项目,其中的一个模块使用到了照片,但是发现了一个很严重的问题。当你在使用Unity的时候,它竟然不按照顺序读取?这个机器人是不是逻辑有问题?如下图: 名字脱敏了哈。。。 照片比较多&…...
pdf怎么标注红色方框?五种PDF标注红色方框方法
pdf怎么标注红色方框?在当今数字化时代,PDF文档已成为我们日常工作和学习中不可或缺的一部分。然而,如何在海量的PDF文件中快速、准确地标注出重要信息,让内容更加醒目呢?今天,我将向大家介绍五种PDF标注红…...

C++字符串细节,面试题06
文章目录 22. 字符串22.1. 字符数组 vs 字符指针 vs 常量字符指针 vs string22.2. strcpy vs sprintf vs memcpy22.3. strlen vs length vs size vs sizeof22.4. 字符串之间的转换22.5 其他数据类型与字符串之间的转换22.6 字符串分割 22. 字符串 22.1. 字符数组 vs 字符指针 …...
AutoModelForCausalLM.from_pretrained 函数调用本地权重报错
文章目录 1、代码报错的位置(前情提要)finetune_lora.shfintune_clm_lora.py 2、报错截图2.1、huggingfaces上的 meta-llama/Llama-2-7b-chat-hf2.2、服务器上模型文件路径 3、特别注意事项 1、代码报错的位置(前情提要) 在终端直…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
