综合模型及应用(图论学习总结部分内容)
文章目录
- 前言
- 六、综合模型及应用(以题目总结为主)
- 分层图思想(包括拆点建图)
- e g 1 : 通信线路 eg1:通信线路 eg1:通信线路[A-Telephone Lines](https://ac.nowcoder.com/acm/contest/1055/A)(蓝书例题)
- e g 2 : 小雨坐地铁 eg2:小雨坐地铁 eg2:小雨坐地铁 [1012-小雨坐地铁(nowcoder.com)](https://ac.nowcoder.com/acm/contest/26077/1012)
- e g 3 : G . B i c y c l e s eg3: G. Bicycles eg3:G.Bicycles [Problem - 1915G - Codeforces](https://codeforces.com/problemset/problem/1915/G)(注意带点贪心剪枝)
- e g 4 : R i n n e L o v e s G r a p h eg4: Rinne\ Loves\ Graph eg4:Rinne Loves Graph [NC22594, 1031-Rinne Loves Graph(nowcoder.com)](https://ac.nowcoder.com/acm/contest/26077/1031)
- 平面图思想
- 最短路图
- 其他
- 一些综合题
- e g 1 : eg1: eg1: [C-Decrement on the Tree](https://ac.nowcoder.com/acm/contest/80999/C)(2020牛客多校第十场 / 2024牛客五一集训派对Day 3)
- e g 3 : eg3: eg3: [K-Stack_2024牛客五一集训day5 / 2021牛客暑期多校2](https://ac.nowcoder.com/acm/contest/81001/K)
- e g 4 eg 4 eg4:Permutation\ Puzzle $ [ 2022 C C P C G u i l i n − J 2022\ CCPC\ Guilin - J 2022 CCPC Guilin−J ](https://codeforces.com/gym/104008/problem/J)(金牌题,拓扑排序+DP+贪心)
- 搭平台建图
- 最小树形图
- 模型综合运用练习题
前言
由于图论学习总结内容过多,全放在一篇博客过于冗长现进行拆分,本文是综合模型及应用部分,其他部分地址见:图论学习总结(For XCPC)
六、综合模型及应用(以题目总结为主)
分层图思想(包括拆点建图)
e g 1 : 通信线路 eg1:通信线路 eg1:通信线路A-Telephone Lines(蓝书例题)
题目大意

解法一:动态规划
仿照动态规划的思想,用 d i s t [ x , i ] dist[x,i] dist[x,i] 表示从 1 1 1 到达 x x x,途中已经指定了 i i i 条电缆免费时,经过路径上最贵的边的花费的最小值。若有一条边 w ( x , y ) w(x,y) w(x,y) 则 d i s t [ y , i ] = max ( d i s t [ x , i ] , w ) dist[y,i] = \max(dist[x,i],w) dist[y,i]=max(dist[x,i],w), d i s t [ y , i + 1 ] = d i s t [ x , i ] dist[y,i+1] = dist[x,i] dist[y,i+1]=dist[x,i]。两个式子分别表示不用免费的升级服务,用一次免费的升级服务。可以看到我们的状态转移明显是有后效性的,一种解决方案是利用迭代的思想,借助 S P F A SPFA SPFA算法就行动规,直至所有状态收敛。对于特殊构造的数据 S P F A SPFA SPFA 的时间复杂度可能退化为 O ( N M ) O(NM) O(NM),谨慎使用。
解法二:分层图最短路
从最短路问题的角度去理解,图中的结点可以扩展到二维元组 ( x , i ) (x,i) (x,i) 表示一个结点。对于边 w ( x , y ) w(x,y) w(x,y),我们可以在分层图中 ( x , i ) (x,i) (x,i) 到 ( y , i + 1 ) (y,i+1) (y,i+1) 连一条边权为 0 0 0 的有向边,那么我们就构造出了一个 N × K N\times K N×K 个点 ( N + P ) × K (N+P)\times K (N+P)×K 条边的分层图。其中不同层之间的有向边帮助我们确保了答案的计算只能从低层向高层转移,解决了后效性问题。这类广义的最短路问题被称为分层图最短路问题,我们可以直接在分层图上跑 D i j k s t r a Dijkstra Dijkstra 即可得到答案。 时间复杂度为 O ( ( N + P ) K log ( N K ) ) O((N+P)K\log(NK)) O((N+P)Klog(NK))。
解法三:二分答案+ 01 B F S 01BFS 01BFS
我们进一步思考本题答案的性质,当支付的钱更多时,合法的升级方案一定包含了花费更少的升级方案,也就是说当 K K K 确定时,我们花费的钱更多,合法的方案也就更多,方案数有单调性,我们考虑二分答案,那么问题就转化为:是否存在合法的方案使得花费不超过 m i d mid mid。
对于 c h e a k cheak cheak 函数,我们只需要将花费小于等于 m i d mid mid 的边权设为 0 0 0,其余设为 1 1 1,我们可以用双端队列 B F S BFS BFS 求出边权只包含 0 / 1 0/1 0/1 的单源最短路问题。判断是否 d i s t [ n ] ≤ K dist[n]\le K dist[n]≤K 即可。时间复杂度为 O ( ( N + P ) log max L ) O((N+P)\log \max_L) O((N+P)logmaxL)
ac代码参考:分层图最短路 、二分答案+ 01 B F S 01BFS 01BFS
e g 2 : 小雨坐地铁 eg2:小雨坐地铁 eg2:小雨坐地铁 1012-小雨坐地铁(nowcoder.com)
题目大意

e g 3 : G . B i c y c l e s eg3: G. Bicycles eg3:G.Bicycles Problem - 1915G - Codeforces(注意带点贪心剪枝)
题目大意
All of Slavic’s friends are planning to travel from the place where they live to a party using their bikes. And they all have a bike except Slavic. There are n n n cities through which they can travel. They all live in the city 1 1 1 and want to go to the party located in the city n n n. The map of cities can be seen as an undirected graph with n n n nodes and m m m edges. Edge i i i connects cities u i u_i ui and v i v_i vi and has a length of w i w_i wi.
Slavic doesn’t have a bike, but what he has is money. Every city has exactly one bike for sale. The bike in the i i i-th city has a slowness factor of s i s_{i} si. Once Slavic buys a bike, he can use it whenever to travel from the city he is currently in to any neighboring city, by taking w i ⋅ s j w_i \cdot s_j wi⋅sj time, considering he is traversing edge i i i using a bike j j j he owns.
Slavic can buy as many bikes as he wants as money isn’t a problem for him. Since Slavic hates traveling by bike, he wants to get from his place to the party in the shortest amount of time possible. And, since his informatics skills are quite rusty, he asks you for help.
What’s the shortest amount of time required for Slavic to travel from city 1 1 1 to city n n n? Slavic can’t travel without a bike. It is guaranteed that it is possible for Slavic to travel from city 1 1 1 to any other city.
e g 4 : R i n n e L o v e s G r a p h eg4: Rinne\ Loves\ Graph eg4:Rinne Loves Graph NC22594, 1031-Rinne Loves Graph(nowcoder.com)
题目大意

rating 2400
平面图思想
最短路图
其他
一些综合题
e g 1 : eg1: eg1: C-Decrement on the Tree(2020牛客多校第十场 / 2024牛客五一集训派对Day 3)
题面

题目分析
- 题目大意是给你一棵树要支持边权修改,每次操作选一条路径,把路径上的边权全部减少 1 1 1。问减到 0 0 0 的最小次数。
- 读完题我们发现,其实我们要将这棵树拆分成诺干条简单路径。
- 这样我们就转化成每个点需要占用多少次路径使其减为一,我们可以考虑点的连边情况,我们可以贪心的想,对于一个点的出和入能多匹配就多匹配。
- 怎么使其能覆盖就覆盖呢?
- 如果 m a x ≤ s u m / 2 max \le sum/2 max≤sum/2,则会多出 s u m % 2 sum\%2 sum%2 的数量
- 如果 m a x > s u m / 2 max>sum/2 max>sum/2,则会多出 2 × m a x − s u m 2\times max-sum 2×max−sum 的数量
- 看到在带边权的树上操作,我们一个惯用的套路就是:边权转点权。
- 这样我们只需要把这些加起来除个2就好了。
- 边权修改的话
ac代码参考:代码查看 (nowcoder.com)
e g 3 : eg3: eg3: K-Stack_2024牛客五一集训day5 / 2021牛客暑期多校2
题目大意

题目分析
e g 4 eg 4 eg4:Permutation\ Puzzle $ 2022 C C P C G u i l i n − J 2022\ CCPC\ Guilin - J 2022 CCPC Guilin−J (金牌题,拓扑排序+DP+贪心)
题目大意
Little r e l y t 871 relyt871 relyt871 is solving a puzzle. The key to the puzzle is a permutation containing numbers 1 … n 1 \dots n 1…n. The values at some positions of the permutation are already fixed, and r e l y t 871 relyt871 relyt871 needs to fill numbers into the remaining positions.
Besides, little r e l y t 871 relyt871 relyt871 has gathered m m m extra requirements about the permutation. Let the solution be represented as p 1 , p 2 , . . . , p n p_1,p_2,...,p_n p1,p2,...,pn, each clue is a pair of indices ( u i , v i ) (u_i,v_i) (ui,vi), which means that p u i < p v i p_{u_i} < p_{v_i} pui<pvi should be satisfied in the solution.
Little r e l y t 871 relyt871 relyt871 wonders if all requirements may be satisfied at the same time. Write a program to find a valid solution when there is one.
题目分析
这是一道灵活运用 拓扑排序 + D P 拓扑排序+DP 拓扑排序+DP求最短路的构造题,想到图论不难,难点是想到用图论算法这么做。
根据所给限制建图,将 p u < p v p_u < p_v pu<pv 的限制视为一条 u → v u → v u→v 的单向边,题目保证会得到一个 D A G DAG DAG。 设在 D A G DAG DAG 上存在一条从 𝑢 到 𝑣 的边数为 k k k 的路径,若 p u p_u pu 已知而 p v p_v pv 未知,则可以推出 p v ≥ p u + k p_v ≥ p_u +k pv≥pu+k; 若 p u p_u pu 未知而 p v p_v pv 已知,则可以推出 p u ≤ p v − k p_u ≤ p_v − k pu≤pv−k。 首先我们通过上述规则推导出所有位置的取值范围 [ L i , R i ] [L_i , R_i] [Li,Ri]。对于已知位置,显然 L i = R i = P i L_i = R_i = P_i Li=Ri=Pi,对于未知位置,可以用 拓扑排序 + d p 拓扑排序 + dp 拓扑排序+dp 来求解。先正向拓扑排序求出 L L L:对于边 (𝑢, 𝑣),做转移 L v = max ( L v , L u + 1 ) L_v = \max(L_v, L_u + 1) Lv=max(Lv,Lu+1),然后反向拓扑排序求出 R R R:对于边 (𝑢, 𝑣),做转移 R u = min ( R u , R v − 1 ) R_u = \min(R_u, R_v − 1) Ru=min(Ru,Rv−1)。
于是转化为如下问题:给定 𝑘 个区间和 𝑘 个互不相同的数,我们需要给每个数匹配一个包含它的区间,此外每个区间匹配的数还要满足一些拓扑关系(形如 P u < P v P_u<P_v Pu<Pv的约束)。如果暂时不考虑拓扑关系的话是一个经典问题,存在一个简单的贪心做法:从小到大枚举所有数,当枚举到 𝑥 时,从所有左端点 ≤ x ≤ x ≤x 且还没被匹配的区间中,选择右端点最小的那个匹配给 𝑥,这个过程用优先队列优化。
然后分析一下区间的性质:如果存在边 (𝑢, 𝑣),根据转移方程可得 L u + 1 ≤ L v , R u + 1 ≤ R v L_u + 1 ≤ L_v,R_u + 1 ≤ R_v Lu+1≤Lv,Ru+1≤Rv,按照上述贪心做法, [ L u , R u ] [L_u, R_u] [Lu,Ru] 一定比 [ L v , R v ] [L_v, R_v] [Lv,Rv] 更早被匹配到,即一定满足 P u < P v P_u < P_v Pu<Pv。所以直接贪心求出来的就是原问题的合法解,如果贪心无解则原问题一定无解。 总时间复杂度 O ( m + n log n ) O(m + n \log n) O(m+nlogn)。
启发:对于 拓扑排序 + D P 拓扑排序+DP 拓扑排序+DP不仅可以用来就 D A G DAG DAG的最短路,对于这种可行解的构造问题,我们可以用 拓扑排序 + D P 拓扑排序+DP 拓扑排序+DP将答案优化到一个区间内,此时可能会将问题转化为另一个较简单直白的问题,如本题转化为了一个简单的贪心问题。当然,对于一些构造题,可能对于一些限制条件,使得答案符合一种拓扑关系,即可考虑使用拓扑排序限制合法答案,或直接进行构造。
ac代码参考:[Submission #256911647 - Codeforces
搭平台建图
e g 1 : eg1: eg1:Meeting (nowcoder.com)(UVALive7250 / hduoj 5521,15年沈阳站银牌题)
题目大意

输入描述,注意数据范围
The first line contains an integer T ( 1 ≤ T ≤ 6 ) T (1≤T≤6) T(1≤T≤6), the number of test cases. Then T T T test cases
follow.
The first line of input contains n n n and m m m. 2 ≤ n ≤ 1 0 5 2≤n≤10^5 2≤n≤105. The following m lines describe the sets E i ( 1 ≤ i ≤ m ) E_i (1≤i≤m) Ei(1≤i≤m). Each line will contain two integers t i ( 1 ≤ t i ≤ 1 0 9 ) t_i(1≤t_i≤10^9) ti(1≤ti≤109) and S i ( S i > 0 ) S_i (S_i>0) Si(Si>0) firstly. Then S i S_i Si integer follows which are the labels of blocks in E i E_i Ei. It is guaranteed that ∑ S i ≤ 1 0 6 ∑S_i≤10^6 ∑Si≤106.
e g 2 : eg2: eg2: Problem - 1941G - Codeforces(搭平台跑最短路,相当于把图集合化,cf rating 2000)
题目大意
Building bridges did not help Bernard, and he continued to be late everywhere. Then Rudolf decided to teach him how to use the subway.
Rudolf depicted the subway map as an undirected connected graph, without self-loops, where the vertices represent stations. There is at most one edge between any pair of vertices.
Two vertices are connected by an edge if it is possible to travel directly between the corresponding stations, bypassing other stations. The subway in the city where Rudolf and Bernard live has a color notation. This means that any edge between stations has a specific color. Edges of a specific color together form a subway line. A subway line cannot contain unconnected edges and forms a connected subgraph of the given subway graph.
An example of the subway map is shown in the figure.

Rudolf claims that the route will be optimal if it passes through the minimum number of subway lines. Help Bernard determine this minimum number for the given departure and destination stations.
最小树形图
e g 1 : eg1: eg1: [1036-[ S C O I 2012 SCOI2012 SCOI2012] 滑雪与时间胶囊](https://ac.nowcoder.com/acm/contest/26077/1036)
题目大意

模型综合运用练习题
回家的路 (洛谷 P 3831 P3831 P3831 [ S H O I 2012 ] [SHOI2012] [SHOI2012])
Problem - G - Codeforces( 2021 C C P C 2021CCPC 2021CCPC哈尔滨,银牌题,最短路+状压期望DP)
Problem - B - Codeforces( 2023 I C P C 2023ICPC 2023ICPC山东省赛,金牌题,拓扑排序,优先队列优化)
Problem - J - Codeforces( 2023 I C P C 2023ICPC 2023ICPC山东省赛,金牌题,图论背景+位运算,类似于数位DP的思想)
相关文章:

综合模型及应用(图论学习总结部分内容)
文章目录 前言六、综合模型及应用(以题目总结为主)分层图思想(包括拆点建图) e g 1 : 通信线路 eg1:通信线路 eg1:通信线路[A-Telephone Lines](https://ac.nowcoder.com/acm/contest/1055/A)(蓝书例题) e g 2 : 小雨坐地铁 eg2:小雨坐地铁 eg2:小雨坐地铁 [1012-小雨坐…...
2025考研专业课、英语、数学、政治视频大全,整理全了!
考研季又到了,备考的小伙伴们,你们准备好了吗? 时间管理 考研是一场与时间的赛跑,合理安排时间,让复习更高效! - 制定详细的学习计划,每天、每周、每月都有明确目标 - ♂️ 保持一定的学习…...
)
设计模式之策略模式(一)
背景: 下单时有很多情况,有的是用户下单,有的是卡密下单,有的是下游下单,有的是需要唤起支付,有的不需要支付,这样就需要写很多下单接口,下面使用策略模式优化这种情况 代码结构 com.example.order ├── controller │ └── OrderController.java ├── service │ …...

常见网络攻击及解决方案
网络安全是开发中常常会遇到的情况,为什么会遇到网络攻击,网络攻击是如何进行的,如何抵御网络攻击,都是我们需要思考的问题。 为什么会遇到网络攻击? 以下是一些主要的因素: 技术漏洞:软件或操…...
【挑战30天首通《谷粒商城》】-【第一天】【10 番外篇】 解决docker 仓库无法访问 + MobaXterm连接VirtualBox虚拟机
文章目录 课程介绍 1、解决docker 仓库无法访问 2、 MobaXterm连接VirtualBox虚拟机 Stage 1:下载MobaXterm选择适合你的版本 Stage 2:vagrant ssh 连接,开启ssh访问 Stage 2-1:su获取root账号权限,输入密码(默认vagra…...

【C++】每日一题 17 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 可以使用回溯法来解决这个问题。首先定义一个映射关系将数字与字母对应起来…...

vue预览PDF文件的几种方法
1.使用iframe标签预览PDF文件 1.1页面结构 html <iframe:src"fileUrl"id"iframeBox"ref"iframeRef"frameborder"0"style"width: 100%; height: 800px"></iframe>1.2 js代码 export default {data() {return {…...
深度学习入门到放弃系列 - 阿里云人工智能平台PAI部署开源大模型chatglm3
通过深度学习入门到放弃系列 - 魔搭社区完成开源大模型部署调用 ,大概掌握了开源模型的部署调用,但是魔搭社区有一个弊端,关闭实例后数据基本上就丢了,本地的电脑无法满足大模型的配置,就需要去租用一些高性价比的GPU机…...

GPT-4o,AI实时视频通话丝滑如人类,Plus功能免费可用
不开玩笑,电影《她》真的来了。 OpenAI最新旗舰大模型GPT-4o,不仅免费可用,能力更是横跨听、看、说,丝滑流畅毫无延迟,就像在打一个视频电话。 现场直播的效果更是炸裂: 它能感受到你的呼吸节奏…...
【优选算法】——Leetcode——202—— 快乐数
目录 1.题目 2. 题⽬分析: 3.简单证明: 4. 解法(快慢指针): 算法思路: 补充知识:如何求⼀个数n每个位置上的数字的平⽅和。 总结概括 5.代码实现 1.C语言 2.C 1.题目 202. 快乐数 编写一个算法来…...

华大基因CEPO-尹烨说学习与生活
怎么去面对生活和事业中的不确定性? 尹烨说,人类能够对抗不确定性的唯一的办法是,去让自己充电。 主持人问他,“和你同年的也有很多人,他们也可能也在学习,你怎么就能够脱颖而出呢?” 他说&am…...
C#中json数据序列化和反序列化的最简单方法(C#对象和字符串的相互转换)
文章目录 将C#对象转换为json字符串Newtonsoft模块的安装用Newtonsoft将对象转换为json字符串 将json字符串转换为C#对象 将C#对象转换为json字符串 本介绍将基于C#中的第三方库Newtonsoft进行,因此将分为Newtonsoft模块的安装和使用两部分。该模块的优势在于只需要…...

logback 日志脱敏
工具类 CustomLogbackPatternLayoutEncoder.java import ch.qos.logback.classic.encoder.PatternLayoutEncoder;public class CustomLogbackPatternLayoutEncoder extends PatternLayoutEncoder {/*** 正则替换规则*/private LogbackReplaces replaces;/*** 使用自定义 MyLog…...
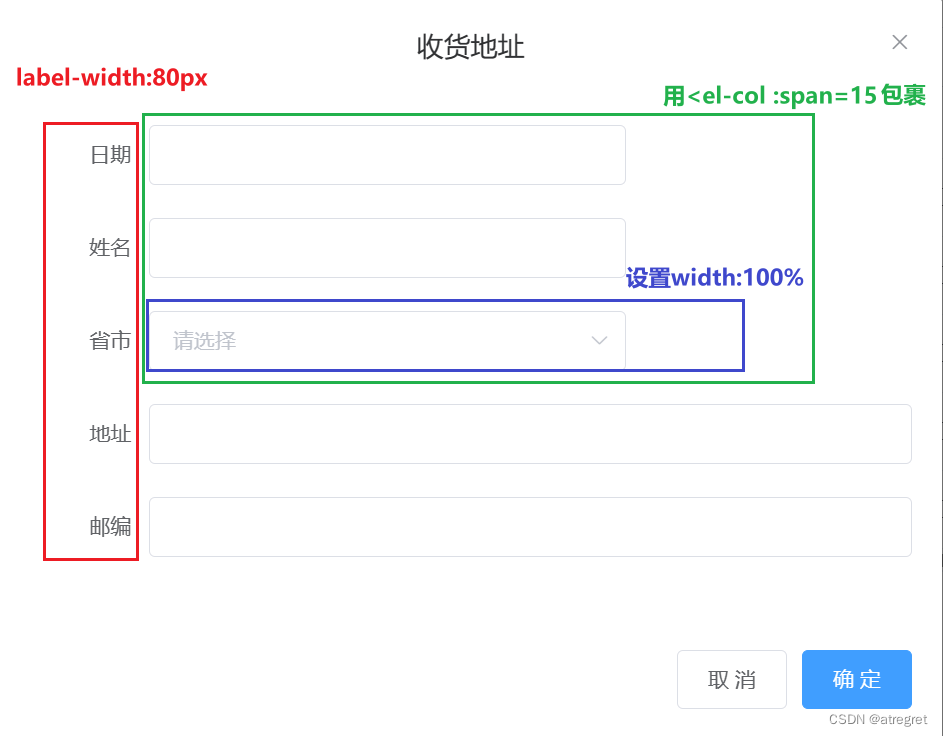
element-ui的表单中,输入框、级联选择器的长度设置
使用<el-col>控制输入框的长度 <el-form-item label"姓名" label-width"80px"><el-col :span"15"><el-input v-model"form.name" autocomplete"off"></el-input></el-col></el-form…...

深入了解 npm:Node.js 包管理工具详解
文章目录 一、npm 基本概念1.1 什么是 npm?1.2 package.json 文件 二、npm 常用命令2.1 初始化项目2.2 安装依赖2.2.1 安装单个包2.2.2 全局安装包2.2.3 安装开发依赖 2.3 移除依赖2.4 更新依赖2.5 查看已安装的包2.6 发布包 三、npm 高级用法3.1 使用 npm scripts3…...

记一次跨域问题
线上跨域问题,在自己配置确认没问题下,要及时找运维看看是不是nginx配置问题。 两个方面: 项目代码 nginx配置 SpringBoot 解决跨域问题的 5 种方案! SpringBoot解决CORS跨域问题 SpringBoot-实现CORS跨域原理及解决方案...
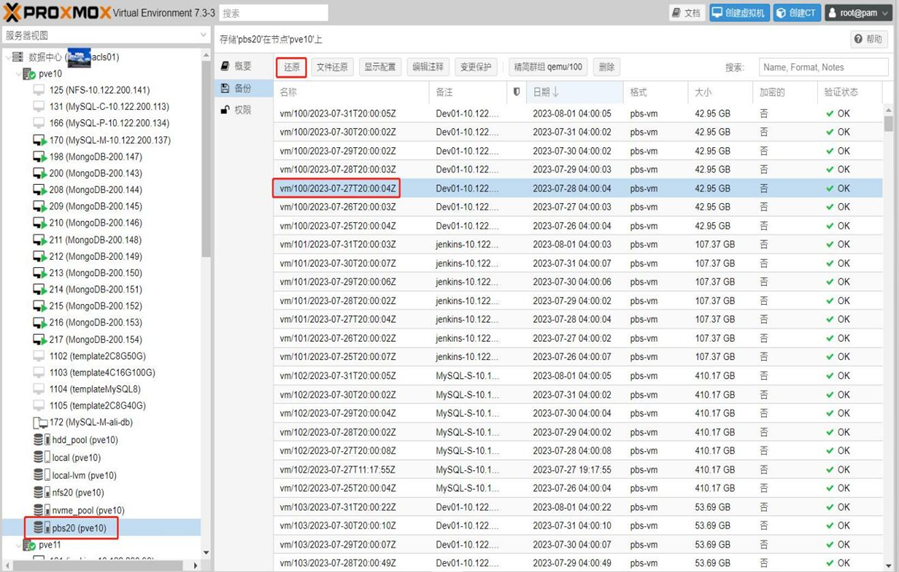
第9章 负载均衡集群日常维护
一个设计良好的高可用负载均衡集群,交付使用以后并不能一劳永逸。欲使其高效、稳定、持续对外服务,日常维护必不可少。 对于高可用负载均衡集群来说,有两种类型的维护形式:常规性维护与突发性维护。突发性维护一般指故障处理&…...

鸿蒙内核源码分析(消息封装篇) | 剖析LiteIpc(上)进程通讯内容
基本概念 LiteIPC是OpenHarmony LiteOS-A内核提供的一种新型IPC(Inter-Process Communication,即进程间通信)机制,为轻量级进程间通信组件,为面向服务的系统服务框架提供进程间通信能力,分为内核实现和用户…...

Charger之三动态电源路径管理(DPPM)
-----本文简介----- 主要内容包括: 领资料:点下方↓名片关注回复:粉丝群 硬件之路学习笔记公众号 Charger的动态电源路径管理(DPPM) 前篇内容:①电池管理IC(Charger)了解一下&…...

大数据模型的选择与安装
大数据模型的选择和安装是一个复杂的过程,涉及多个因素,包括模型的通用能力、特定任务的性能、数据效率、评估完整性、成本以及部署的硬件和软件环境。以下是一些关于大数据模型选择与安装的考虑因素和步骤: 选择大数据模型的考虑因素&#…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
