【C++】每日一题 17 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

可以使用回溯法来解决这个问题。首先定义一个映射关系将数字与字母对应起来,然后使用回溯算法来生成所有可能的组合。
回溯算法是一种通过不断尝试各种可能性来解决问题的方法,通常用于求解组合、排列、子集等问题。它通过深度优先搜索的方式探索问题的所有解空间,并在搜索过程中进行剪枝,从而有效地找到满足特定条件的解。
下面是回溯算法的一般步骤:
选择路径: 从问题的初始状态出发,按照某种规则选择一个候选解的路径,即在问题的解空间中前进一步。
探索路径: 在当前选择的路径上继续向前探索,查找可能的解或部分解。
约束条件: 在探索过程中,判断当前路径是否满足问题的约束条件。如果不满足,则放弃该路径,回退到上一步,继续探索其他路径。
标记状态: 在进入下一层递归之前,通常需要修改问题的状态,以便记录当前路径的选择或处理过程。
回退路径: 当探索到底或者无法继续前进时,需要回退到上一层,撤销当前路径的选择,返回上一层继续探索其他路径。
结束条件: 当搜索到达问题的解空间的边界或者满足特定条件时,结束搜索,得到最终的解或者部分解。
回溯算法的核心思想是通过不断地选择、探索、回退和标记状态,逐步地搜索问题的解空间,直到找到所有满足条件的解或者确定无解。
#include <iostream>
#include <vector>
#include <string>using namespace std;// 定义数字与字母的映射关系
vector<string> keypad = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};// 回溯算法生成所有可能的组合
void backtrack(vector<string>& result, string& digits, string current, int index) {// 如果当前组合的长度等于输入数字的长度,则将当前组合加入结果集if (index == digits.length()) {result.push_back(current);return;}// 获取当前数字对应的字母集合string letters = keypad[digits[index] - '0'];// 遍历当前数字对应的每一个字母,进行回溯for (char letter : letters) {current.push_back(letter); // 添加当前字母到当前组合中backtrack(result, digits, current, index + 1); // 递归处理下一个数字current.pop_back(); // 回溯,撤销当前字母}
}vector<string> letterCombinations(string digits) {vector<string> result;if (digits.empty()) return result; // 如果输入为空,则直接返回空结果集string current = "";backtrack(result, digits, current, 0); // 调用回溯算法生成所有可能的组合return result;
}int main() {string digits = "23";vector<string> combinations = letterCombinations(digits);cout << "所有可能的字母组合:" << endl;for (const string& combination : combinations) {cout << combination << " ";}cout << endl;return 0;
}时间空间复杂度分析
假设输入数字串的长度为 ( n ),每个数字对应的字母集合的平均长度为 ( m )。
时间复杂度分析:
回溯算法:
对于每个数字,我们都需要尝试其对应的所有字母,这需要 ( O(m) ) 的时间。
由于有 ( n ) 个数字,因此总共的时间复杂度为 ( O(m^n) )。
结果集合生成:
生成结果集合的过程中,需要将所有可能的组合添加到结果集中,这也需要 ( O(m^n) ) 的时间。
综合起来,整个算法的时间复杂度为 ( O(m^n) )。
空间复杂度分析:
递归调用栈:
递归调用栈的深度最多为输入数字串的长度 ( n ),因此需要额外的 ( O(n) ) 的空间。
结果集合:
存储结果集合所需的空间取决于结果的数量。最坏情况下,结果数量为 ( O(m^n) ),因此需要 ( O(m^n) ) 的空间。
综合起来,整个算法的空间复杂度为 ( O(m^n) )。
总的来说,这个算法的时间和空间复杂度都是指数级别的,随着输入规模 ( n ) 和每个数字对应的字母集合的大小 ( m ) 的增加,其运行时间和所需空间将急剧增加。
相关文章:

【C++】每日一题 17 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 可以使用回溯法来解决这个问题。首先定义一个映射关系将数字与字母对应起来…...

vue预览PDF文件的几种方法
1.使用iframe标签预览PDF文件 1.1页面结构 html <iframe:src"fileUrl"id"iframeBox"ref"iframeRef"frameborder"0"style"width: 100%; height: 800px"></iframe>1.2 js代码 export default {data() {return {…...
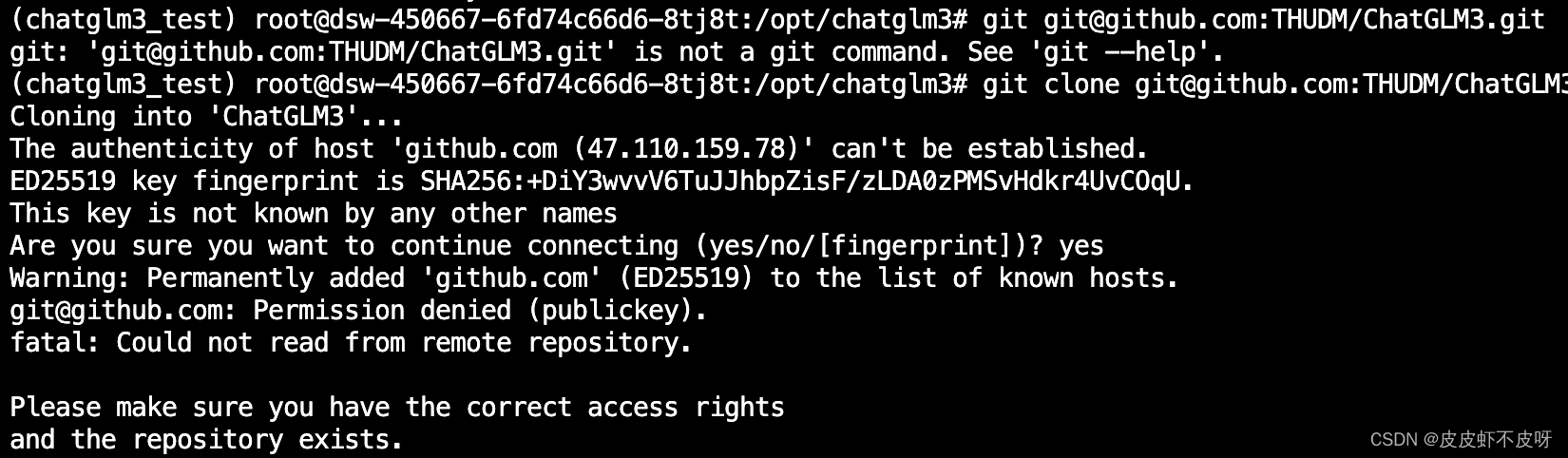
深度学习入门到放弃系列 - 阿里云人工智能平台PAI部署开源大模型chatglm3
通过深度学习入门到放弃系列 - 魔搭社区完成开源大模型部署调用 ,大概掌握了开源模型的部署调用,但是魔搭社区有一个弊端,关闭实例后数据基本上就丢了,本地的电脑无法满足大模型的配置,就需要去租用一些高性价比的GPU机…...

GPT-4o,AI实时视频通话丝滑如人类,Plus功能免费可用
不开玩笑,电影《她》真的来了。 OpenAI最新旗舰大模型GPT-4o,不仅免费可用,能力更是横跨听、看、说,丝滑流畅毫无延迟,就像在打一个视频电话。 现场直播的效果更是炸裂: 它能感受到你的呼吸节奏…...
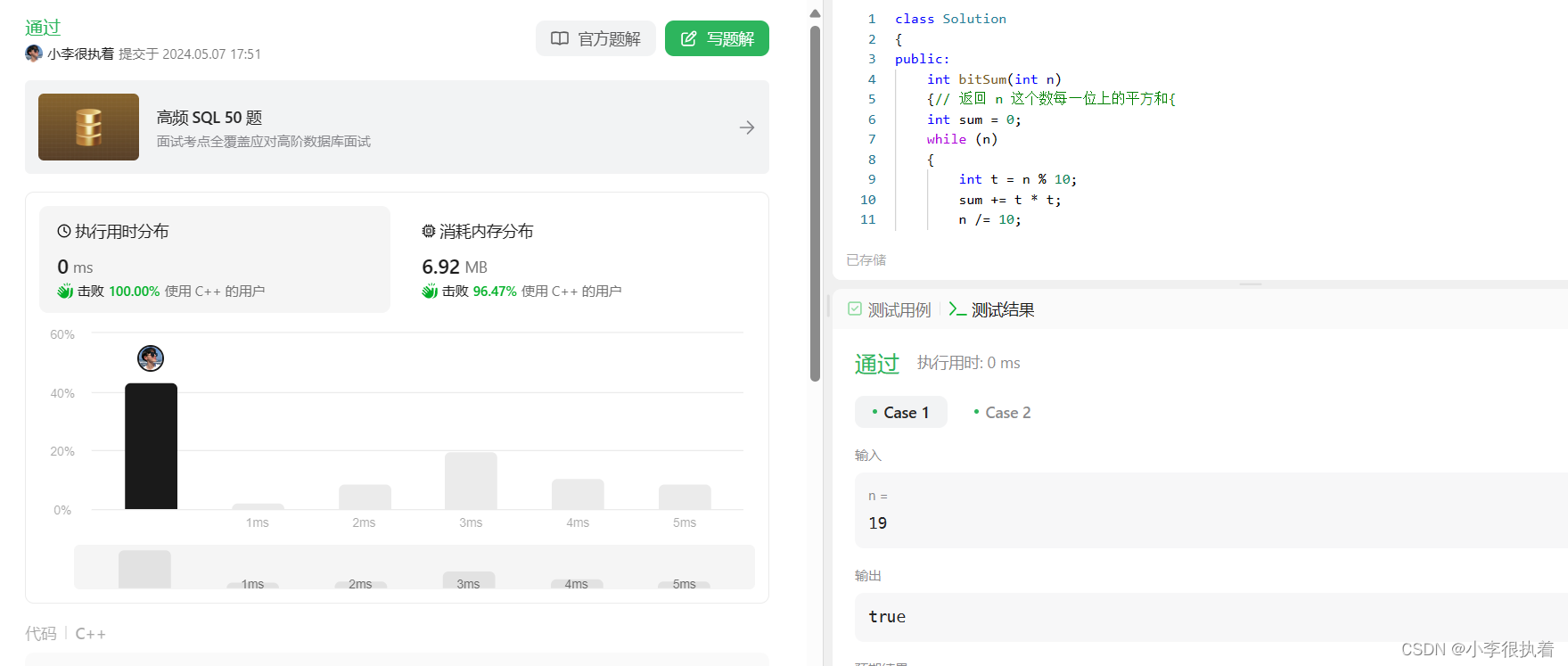
【优选算法】——Leetcode——202—— 快乐数
目录 1.题目 2. 题⽬分析: 3.简单证明: 4. 解法(快慢指针): 算法思路: 补充知识:如何求⼀个数n每个位置上的数字的平⽅和。 总结概括 5.代码实现 1.C语言 2.C 1.题目 202. 快乐数 编写一个算法来…...

华大基因CEPO-尹烨说学习与生活
怎么去面对生活和事业中的不确定性? 尹烨说,人类能够对抗不确定性的唯一的办法是,去让自己充电。 主持人问他,“和你同年的也有很多人,他们也可能也在学习,你怎么就能够脱颖而出呢?” 他说&am…...
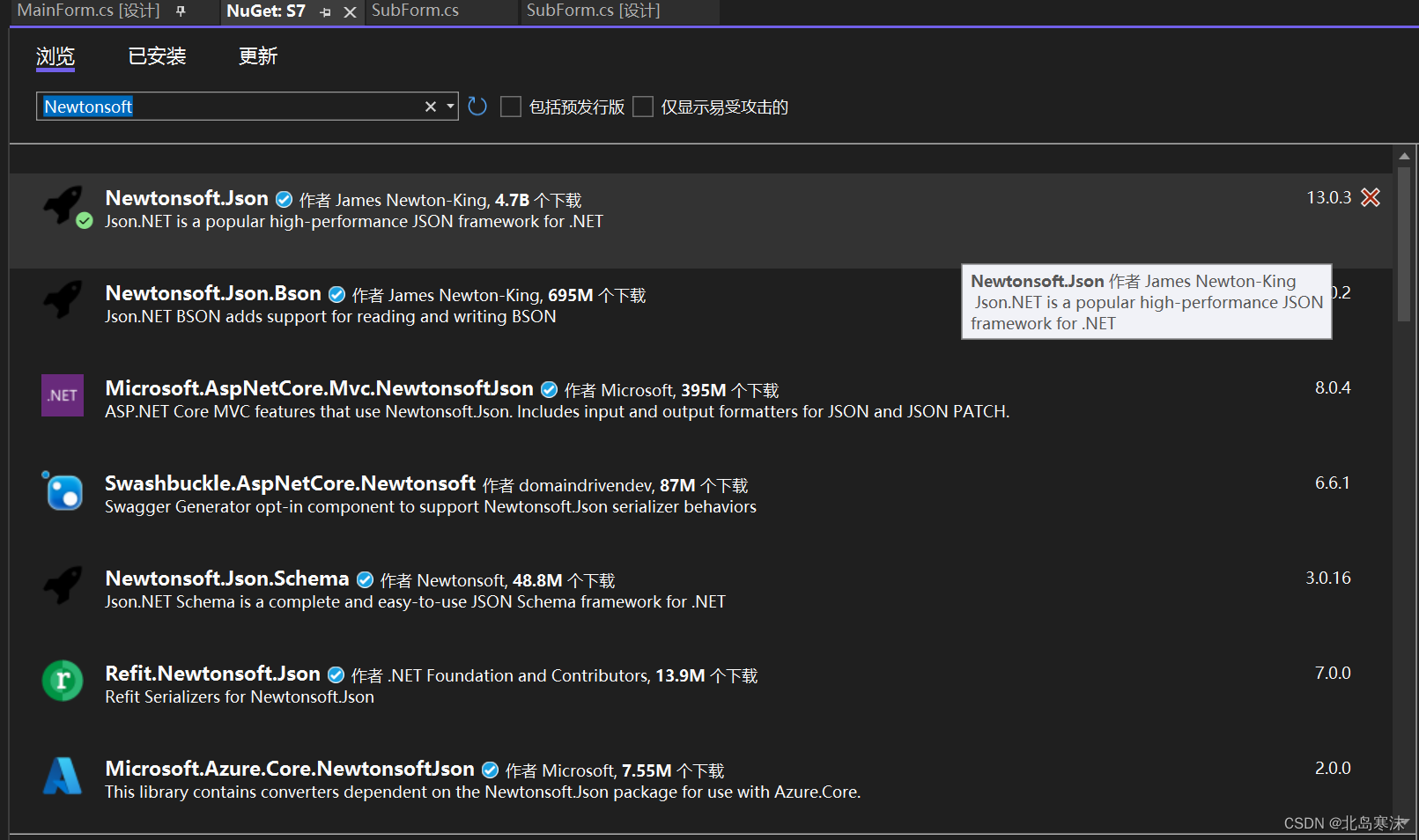
C#中json数据序列化和反序列化的最简单方法(C#对象和字符串的相互转换)
文章目录 将C#对象转换为json字符串Newtonsoft模块的安装用Newtonsoft将对象转换为json字符串 将json字符串转换为C#对象 将C#对象转换为json字符串 本介绍将基于C#中的第三方库Newtonsoft进行,因此将分为Newtonsoft模块的安装和使用两部分。该模块的优势在于只需要…...

logback 日志脱敏
工具类 CustomLogbackPatternLayoutEncoder.java import ch.qos.logback.classic.encoder.PatternLayoutEncoder;public class CustomLogbackPatternLayoutEncoder extends PatternLayoutEncoder {/*** 正则替换规则*/private LogbackReplaces replaces;/*** 使用自定义 MyLog…...
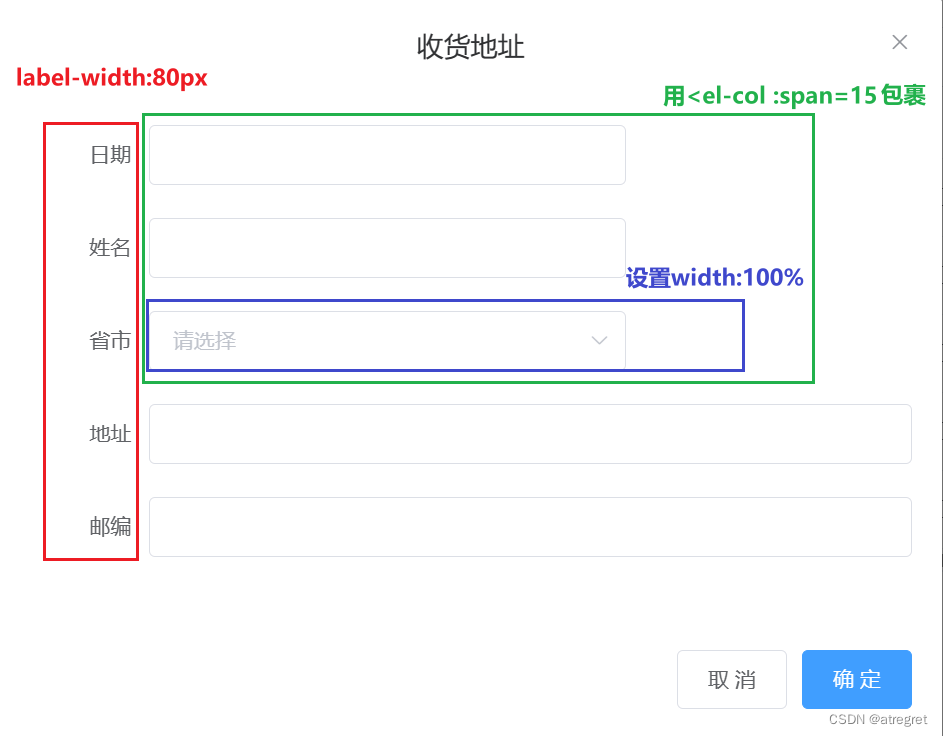
element-ui的表单中,输入框、级联选择器的长度设置
使用<el-col>控制输入框的长度 <el-form-item label"姓名" label-width"80px"><el-col :span"15"><el-input v-model"form.name" autocomplete"off"></el-input></el-col></el-form…...

深入了解 npm:Node.js 包管理工具详解
文章目录 一、npm 基本概念1.1 什么是 npm?1.2 package.json 文件 二、npm 常用命令2.1 初始化项目2.2 安装依赖2.2.1 安装单个包2.2.2 全局安装包2.2.3 安装开发依赖 2.3 移除依赖2.4 更新依赖2.5 查看已安装的包2.6 发布包 三、npm 高级用法3.1 使用 npm scripts3…...

记一次跨域问题
线上跨域问题,在自己配置确认没问题下,要及时找运维看看是不是nginx配置问题。 两个方面: 项目代码 nginx配置 SpringBoot 解决跨域问题的 5 种方案! SpringBoot解决CORS跨域问题 SpringBoot-实现CORS跨域原理及解决方案...
第9章 负载均衡集群日常维护
一个设计良好的高可用负载均衡集群,交付使用以后并不能一劳永逸。欲使其高效、稳定、持续对外服务,日常维护必不可少。 对于高可用负载均衡集群来说,有两种类型的维护形式:常规性维护与突发性维护。突发性维护一般指故障处理&…...

鸿蒙内核源码分析(消息封装篇) | 剖析LiteIpc(上)进程通讯内容
基本概念 LiteIPC是OpenHarmony LiteOS-A内核提供的一种新型IPC(Inter-Process Communication,即进程间通信)机制,为轻量级进程间通信组件,为面向服务的系统服务框架提供进程间通信能力,分为内核实现和用户…...

Charger之三动态电源路径管理(DPPM)
-----本文简介----- 主要内容包括: 领资料:点下方↓名片关注回复:粉丝群 硬件之路学习笔记公众号 Charger的动态电源路径管理(DPPM) 前篇内容:①电池管理IC(Charger)了解一下&…...

大数据模型的选择与安装
大数据模型的选择和安装是一个复杂的过程,涉及多个因素,包括模型的通用能力、特定任务的性能、数据效率、评估完整性、成本以及部署的硬件和软件环境。以下是一些关于大数据模型选择与安装的考虑因素和步骤: 选择大数据模型的考虑因素&#…...
(十七))
React 之 lazy(延迟加载)(十七)
lazy 能够让你在组件第一次被渲染之前延迟加载组件的代码。 在组件外部调用 lazy,以声明一个懒加载的 React 组件: import { lazy } from react;const MarkdownPreview lazy(() > import(./MarkdownPreview.js)); 配合 Suspense 实现懒加载组件 //App.js imp…...

Node.js -- 会话控制
文章目录 1. 会话介绍2. cookie 相关操作2.1 cookie 设置2.2 删除 cookie2.3 获取cookie 3. session 相关操作4. cookie 和session 的区别5. 补充知识 -- CSRF跨站请求伪造6. token 1. 会话介绍 所谓会话控制就是对会话进行控制 HTTP是一种无状态的协议,它没有办法…...
做抖店不能踩的几个坑,新手要照做,老玩家要听劝~
我是王路飞。 很多人都说抖店的运营很简单,选选品、对接一下达人,就可以坐等店铺出单了。 这话骗骗还没开店的小白也就得了,但凡做抖店超过一个月的,都不会相信这句话。 细心耐心是做抖店最基本的态度。 拿到一个好结果的前提…...
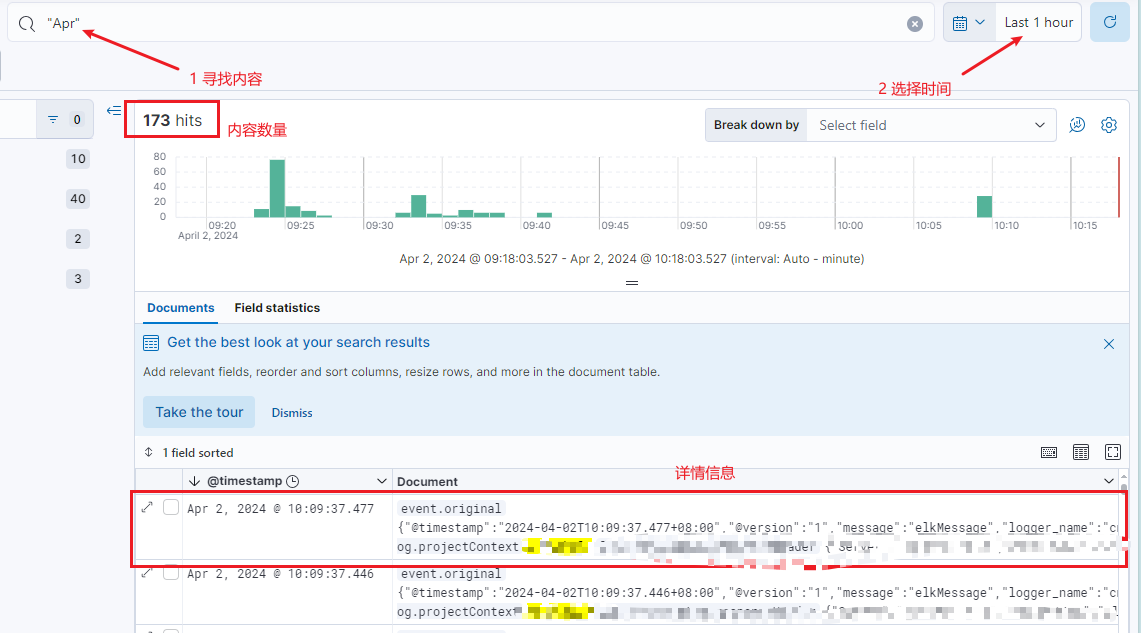
【Kibana】快速上手Kibana平台(KQL)
文章目录 快速使用Kibana平台常用查询语句KQL基本查询覆合查询模糊查询 目前市面上大部分的公司的日志系统都是使用ELK系统,因此我们进行工作必须得掌握Kibana平台的基本使用,这里主要说明怎么“快速使用Kibana平台”以及记录一些常用的“KQL语言”。 快…...
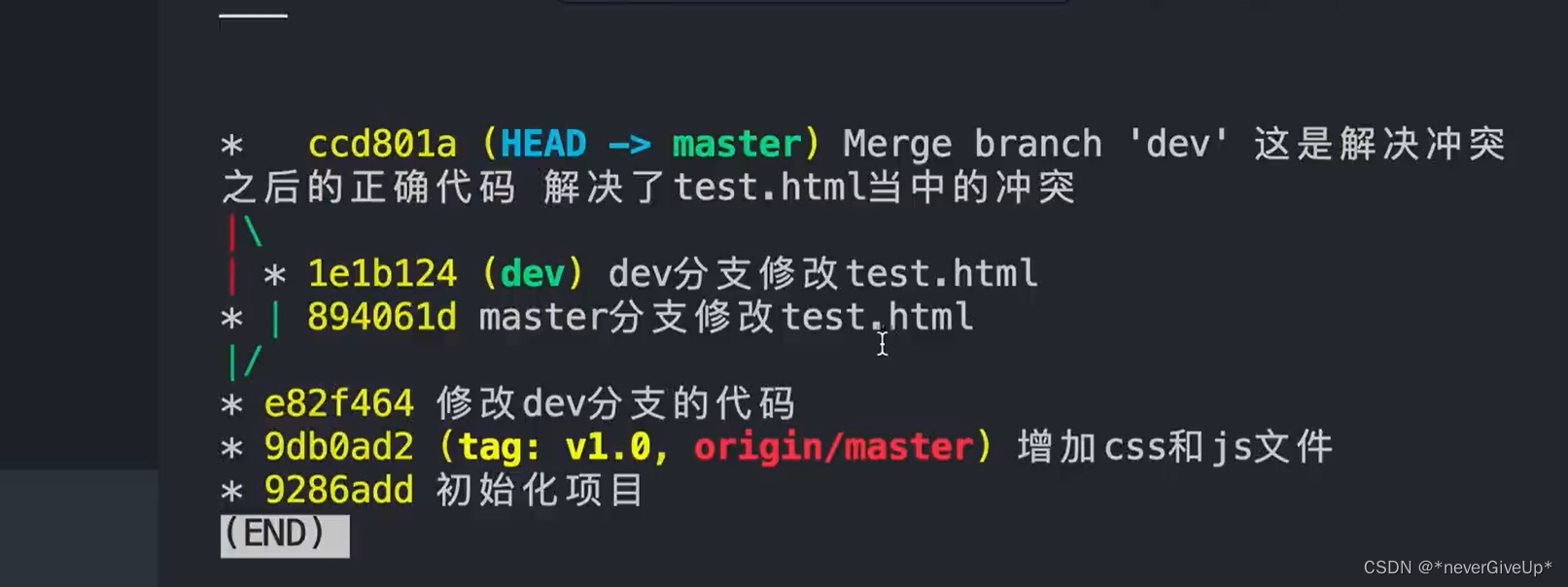
全方位入门git-慕课网 笔记
目录 【上传github忽略某些文件】【配置用户名和邮箱】【想要删除不需要的文件时如何进行操作】【想要给文件重命名如何操作】【想要移动文件到其他位置时如何操作】【文件有变化时,如何查看前后变化】【操作失误的情况下如何实现一键还原】【不再追踪时如何实现撤销…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
