数据结构简单介绍、算法简单介绍、算法复杂度、时间复杂度等的介绍
文章目录
- 前言
- 一、什么是数据结构
- 二、什么是算法
- 三、算法复杂度
- 1. 时间复杂度
- ① 时间复杂度的定义
- ② 大O的渐进表示法
- 总结
前言
数据结构简单介绍、算法简单介绍、算法复杂度、时间复杂度等的介绍
一、什么是数据结构
数据结构是计算机存储,组织数据结构的方式,指相互之间存在一种或多种特定关系的数据元素的集合。
二、什么是算法
算法: 简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
三、算法复杂度
衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的。即时间复杂度和空间复杂度
- 时间复杂度主要衡量一个算法的运行快慢
- 空间复杂度主要衡量一个算法运行所需要的额外空间
- 随着技术发展,计算机存储容量变得非常大,已经不是非常关注空间复杂度,而是更关注时间复杂度。
1. 时间复杂度
① 时间复杂度的定义
- 算法的时间复杂度是一个函数(函数式),一个算法执行所耗费的时间,理论上是不能算出来的,只有运行程序才能知道。
- 但是一个算法所花费的时间与其中语句的执行次数成正比例。
- 所以算法中的基本操作的执行次数,为算法的时间复杂度。
② 大O的渐进表示法
实际计算时间复杂度,不计算精确的执行次数,只需要计算大概执行次数(量级或阶数),我们用大O的渐进表示法。
- 时间复杂度: O(N),习惯用N表示
1、用常数1取代运行时间中的所有加法常数。
int main()
{int count = 0;int M = 10;while (M--){++count;}printf("%d\n", count);
}
- 上述代码执行 M 次 相当于是 10 次, 也就是函数执行的量级是10(常数级),常数级用O(1)表示
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
- 上述代码执行 (2 * N + M)次, 只保留高阶项
- 高阶项存在且不是1,去除常数。
- (2 * N)次,所以Func2的时间复杂度是: O(N)。
有些算法的时间复杂度存在最好、最坏和平均的情况。
在实际中一般情况关注的是算法的最坏运行情况
实例如下:
实例1:
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
- 上述Func4的时间复杂度是:O(1)
实例2:
const char * strchr ( const char * str, int character );
- 上述strchr 的时间复杂度是O(N)
- 按最坏的情况算
实例3:
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 1; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
- 上述BubbleSort的时间复杂度
- 若数组本来就有序(最好情况),则时间复杂度为O(N)
- 若数组无序(最坏情况),则时间复杂度为O(N^2)
- 时间复杂度为O(N^2)
实例4:
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;while (begin <= end){int mid = begin + ((end-begin) / 2);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}
- 上述二分法时间复杂度为 O(logN) 这里的log是以2为底
实例5:
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}
- 上述代码Fac(N) , Fac(N-1), Fac(N-2), …F(0), 共N+1次,所以时间复杂度是O(N)
实例6:
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
- 上述代码调用会调 2 ^ N次,所以时间复杂度为 O(2 ^ N)
实例7
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++ k){++count;}for (int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}
- 上述Func3的时间复杂度是O(M + N)
- 若 M >> N, 则时间复杂度为 O(M)
- 若 N >> M, 则时间复杂度为 O(N)
- 若 M = N, 则时间复杂度为 O(M)或O(N)
- 若没有说明,时间复杂度为O(M + N)
总结
数据结构简单介绍、算法简单介绍、算法复杂度、时间复杂度等的介绍
相关文章:

数据结构简单介绍、算法简单介绍、算法复杂度、时间复杂度等的介绍
文章目录 前言一、什么是数据结构二、什么是算法三、算法复杂度1. 时间复杂度① 时间复杂度的定义② 大O的渐进表示法 总结 前言 数据结构简单介绍、算法简单介绍、算法复杂度、时间复杂度等的介绍 一、什么是数据结构 数据结构是计算机存储,组织数据结构的方式&…...
Google I/O 2024:有关AI的一切已公布|TodayAI
2024年谷歌I/O大会圆满落幕,谷歌在会上发布了一系列更新,涵盖从最新的人工智能技术到Android系统的多项改进。此次大会特别关注于谷歌的Gemini人工智能模型,并详细介绍了这些模型如何被融入到Workspace、Chrome等多个应用程序中,展…...
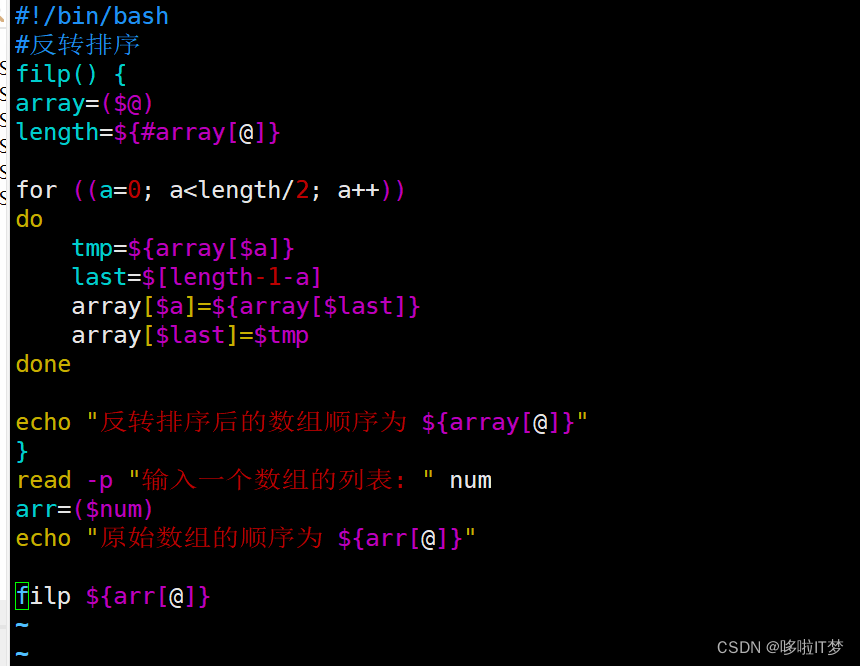
【Shell脚本】Shell编程之数组
目录 一.数组 1.基本概念 2.定义数组的方法 2.1.方法一 2.2.方法二 2.3.方法三 2.4.方法四 2.5.查看数组长度 2.6.查看数组元素下标 3.数组分片 4.数组字符替换 4.1.临时替换 4.2.永久替换 5.数组删除 5.1.删除某个下标 5.2.删除整组 6.数组遍历和重新定义 7…...

Python 全栈系列246 任务调度对象WFlaskAPS
说明 之前已经完全跑通了任务调度,实现了S2S的流转Python 全栈系列243 S2S flask_celery。由于request请求用起来比较别扭,所以创建一个对象来进行便捷操作。 内容 1 功能 WFlaskAPS包含管理定时任务的必要功能 from datetime import datetime from…...

关于Windows中的NTUSER.DAT文件的知识,看这篇文章就差不多了
每个用户配置文件中都隐藏着一个名为NTUSER.DAT的文件。此文件包含每个用户的设置和首选项,因此你不应该删除它,也可能不应该编辑它。Windows会自动为你加载、更改和保存该文件。 NTUSER.DAT包含你的用户配置文件设置 每次更改Windows和已安装程序的外观和行为时,无论是桌…...
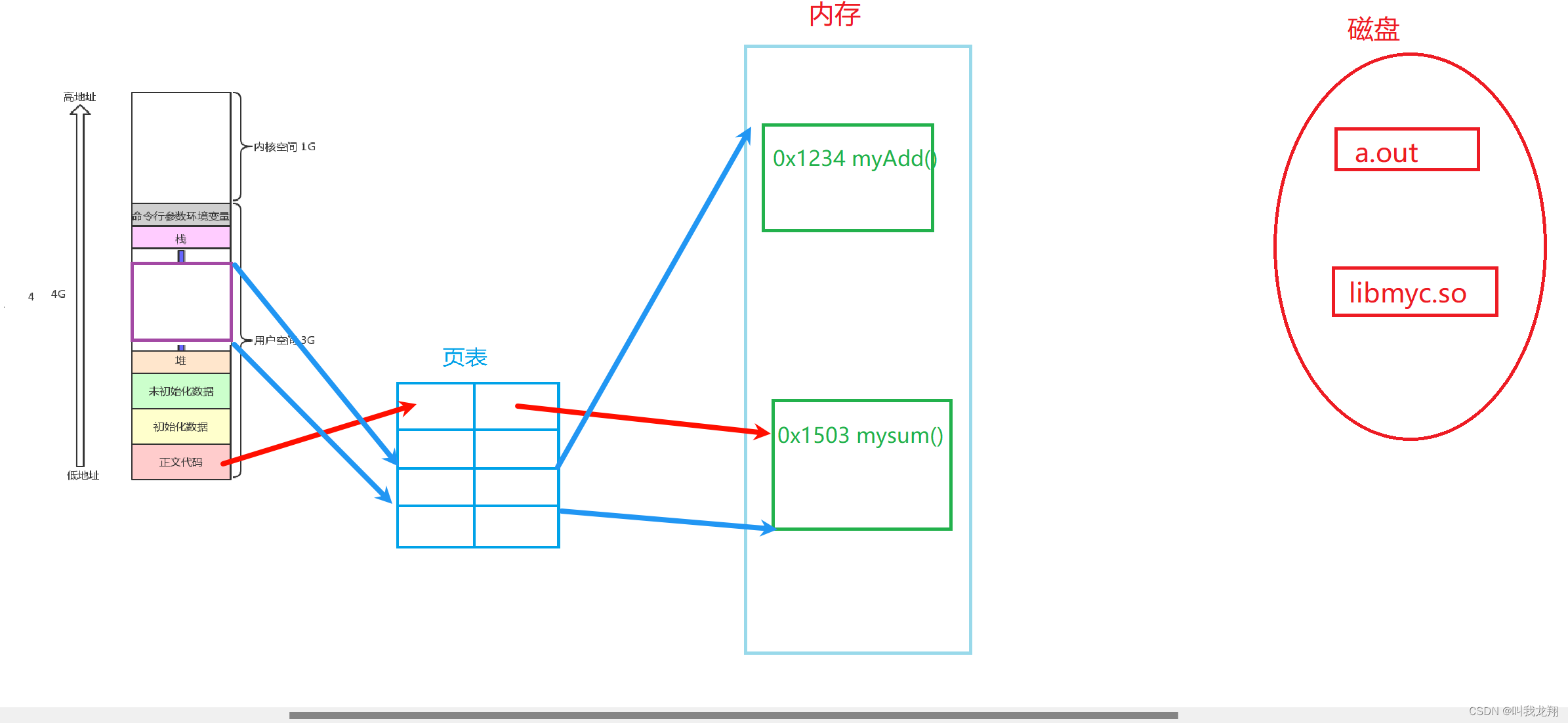
【Linux】动态库与静态库的底层比较
送给大家一句话: 人生最遗憾的,莫过于,轻易地放弃了不该放弃的,固执地坚持了不该坚持的。 – 柏拉图 (x(x_(x_x(O_o)x_x)_x)x) (x(x_(x_x(O_o)x_x)_x)x) (x(x_(x_x(O_o)x_x)_x)x) 底层比较 1 前言2 编译使用比较2 如何加载Than…...

私活更好用:SpringBoot开源项目!!【送源码】
今天分享一款非常香的SpringBoot大屏开源项目,非常适合接私活用。 这是一款基于SpringBoot代码生成器的快速开发平台!采用前后端分离架构:SpringBoot,Mybatis,Shiro,JWT,Vue&Ant Design。强…...
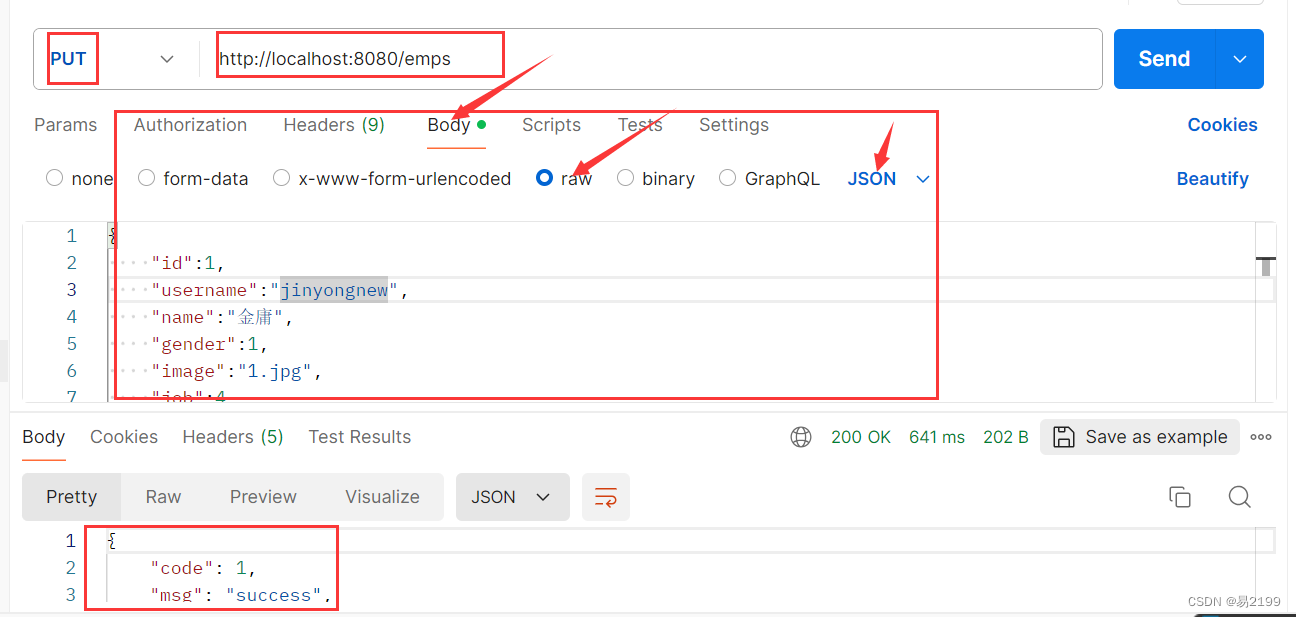
SprintBoot案例-增删改查
黑马程序员JavaWeb开发教程 文章目录 一、准备工作1. 准备数据库表1.1 新建数据库mytlias1.2 新建部门表dept1.3 新建员工表emp 2. 准备一个Springboot工程2.1 新建一个项目 3. 配置文件application.properties中引入mybatis的配置信息,准备对应的实体类3.1 引入myb…...
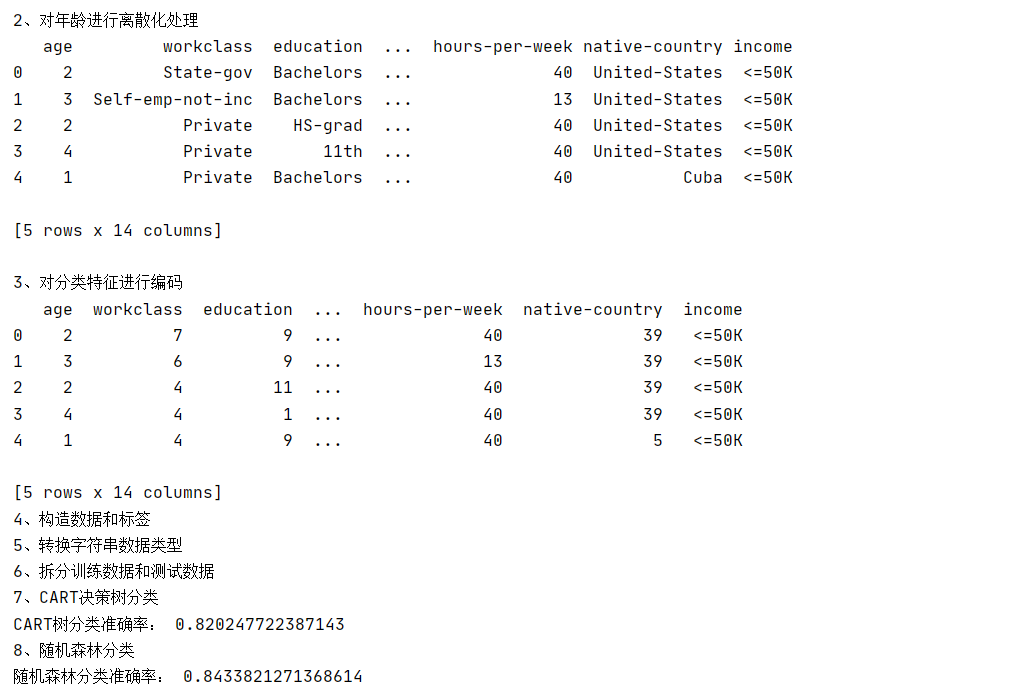
【机器学习】:基于决策树与随机森林对数据分类
机器学习实验报告:决策树与随机森林数据分类 实验背景与目的 在机器学习领域,决策树和随机森林是两种常用的分类算法。决策树以其直观的树形结构和易于理解的特点被广泛应用于分类问题。随机森林则是一种集成学习算法,通过构建多个决策树并…...

.NET 4.8和.NET 8.0的区别和联系、以及查看本地计算机的.NET版本
文章目录 .NET 4.8和.NET 8.0的区别查看本地计算机的.NET版本 .NET 4.8和.NET 8.0的区别 .NET 8.0 和 .NET 4.8 之间的区别主要体现在它们的发展背景、目标平台、架构设计和功能特性上。下面是它们之间的一些主要区别: 发展背景: .NET 4.8 是.NET Fram…...
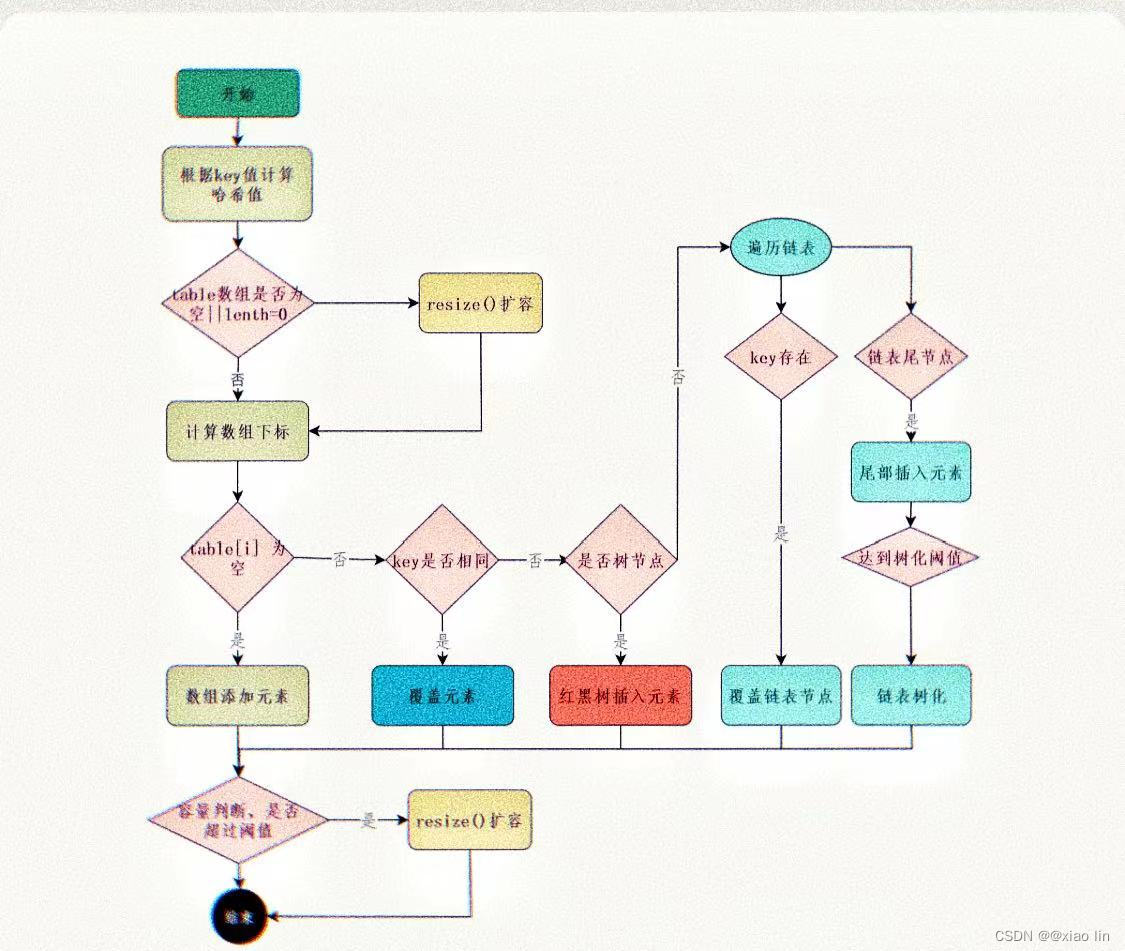
23.HashMap的put方法流程
一、put方法的流程图 二、put方法的执行步骤 首先,根据key值计算哈希值。然后判断table数组是否为空或者数组长度是否为0,是的话则要扩容,resize()。接着,根据哈希值计算数组下标。如果这个下标位置为空&a…...

元类结合__new__
__new__:用来生成骨架 __init__:骨架添加血肉 【一】类中的__new__ class MyClass(object):def __init__(self,name,age):print(f"给当前MyClass类的对象初始化属性的时候会触发__init__")self.name nameself.age age def __call__(self,*args,**kwargs):pri…...

(C语言)队列实现与用队列实现栈
目录 1.队列 1.1队列的概念及结构 1.2 队列的实际应用联想 1.3队列的实现 2. 队列应用——队列实现栈 主要思路 1.队列 1.1队列的概念及结构 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进…...

字符画生成网站 ascii字符画
_____ / ___/__ ___ / /__/ _ \/ _ \ \___/ .__/ .__//_/ /_/ font推荐:1.Slant 2.Small 3.Small slant https://patorjk.com/software/taag/#pdisplay&fSmall%20Slant&tCpp https://www.kammerl.de/ascii/AsciiSignature.php https://asciia…...

【C -> Cpp】由C迈向Cpp (6):静态、友元和内部类
标题:【C -> Cpp】由C迈向Cpp (6):静态、友元和内部类 水墨不写bug (图片来源于网络) 目录 (一)静态成员 (二)友元 (三)…...

探索Playwright:Python下的Web自动化测试革命
在如今这个互联网技术迅速发展的时代,web应用的质量直接关系着企业的声誉和用户的体验。因此,自动化测试成为了保障软件质量的重要手段之一。今天,我将带大家详细了解一款在测试领域大放异彩的神器——Playwright,并通过Python语言…...

先有JVM还是先有垃圾回收器?很多人弄混淆了
是先有垃圾回收器再有JVM呢,还是先有JVM再有垃圾回收器呢?或者是先有垃圾回收再有JVM呢?历史上还真是垃圾回收更早面世,垃圾回收最早起源于1960年诞生的LISP语言,Java只是支持垃圾回收的其中一种。下面我们就来刨析刨析…...
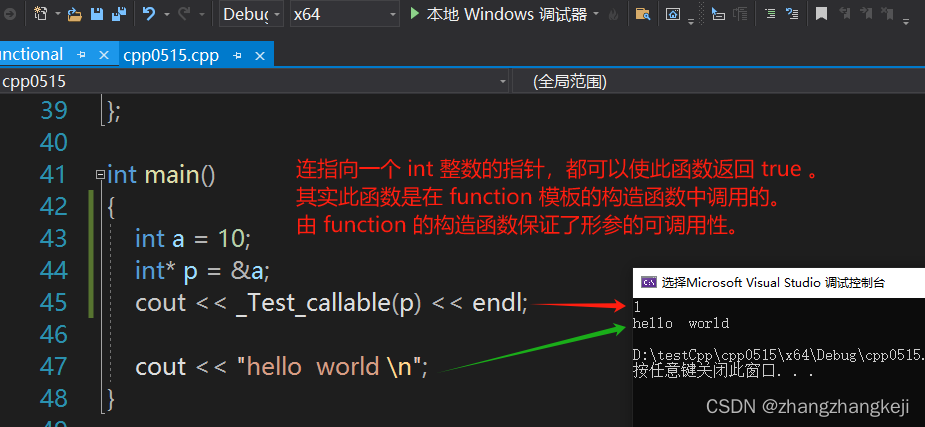
关于 vs2019 c++20 规范里的一个全局函数 _Test_callable
(1)看名思议,觉得这个函数可以测试其形参是否是可以被调用的函数,或可调用对象? 不,这个名字不科学。有误导,故特别列出。看下其源码(该函数位于 头文件): 辅…...

07-Fortran基础--Fortran指针(Pointer)的使用
07-Fortran基础--Fortran指针Pointer的使用 0 引言1 指针(Poionter)的有关内容1.1 一般类型指针1.2 数组指针1.3 派生类(type)指针1.4 函数指针 2 可运行code 0 引言 Fortran是一种广泛使用的编程语言,特别适合科学计算和数值分析。Fortran 9…...

日期差值,
日期差值 ac代码 #include<iostream> using namespace std; int ans0; int get(int n){int mon[14]{0,31,28,31,30,31,30,31,31,30,31,30,31};ans0;int m_dayn%100;int m_month(n/100)%100;int m_year(n/10000);ansm_day;while(m_month--){//加上月数if((m_year%40&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
