Codeforces Round 703 (Div. 2)(A~D)
A. Shifting Stacks

给出一个数组,每次可以将一个位置-1,右侧相邻位置+1,判断是否可以经过若干次操作后使得数列严格递增。
思路:对于每个位置,前缀和必须都大于该位置应该有的最少数字,即第一个位置最少是0, 第二个位置最少是1,第三个位置最少是2,取一下前缀和。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 105;
int t, n;
ll a[N];int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> t;while(t --) {std::cin >> n;ll num = 0;bool flag = true;for(int i = 1; i <= n; i ++) {std::cin >> a[i];a[i] += a[i - 1];if(a[i] < num)flag = false;num += i;}std::cout << (flag ? "YES" : "NO") << '\n';}return 0;
}B. Eastern Exhibition

给出二维平面上若干个坐标,在二维平面上选择一个位置,使得这个位置到所有点的距离之和最小,求满足条件的点有多少个。
思路:考虑先放到一维里考虑,这样很容易想到是放到中间位置,即中间两个点之间的距离都可以;如果放到二维其实也是一样的,就是两个维度的中间两点距离差的乘积。
AC Code:
#include <bits/stdc++.h>
using namespace std;long long solve(vector<int> x) {sort(x.begin(), x.end());return x[x.size() / 2] - x[(x.size() - 1) / 2] + 1;
}void solve() {int n;cin >> n;vector<int> x(n), y(n);for (int i = 0; i < n; ++i)cin >> x[i] >> y[i];cout << solve(x) * solve(y) << '\n';
}int main() {int t;cin >> t;while (t--) solve();return 0;
}os:贴的标解hhh
C. Guessing the Greatest

交互题,每次可以询问任意区间内第二大的数的位置,在不超过20次询问后得到最大值的位置。
思路:20次,可以想到二进制枚举,因为数据范围在1e5内,完全可以完成枚举。考虑倍增,如果一开始的次大值位置为p,若是1~p内存在最大值,则可以用倍增不断增大l,缩减当前范围,到最后最大值一定是l的位置;反之,则用倍增不断缩小r的范围,最后最大值的位置就是r。
AC Code;
#include <bits/stdc++.h>typedef long long ll;
#define int long long
const int N = 1e3 + 5;
int n;
int pow2[25];int ask(int l, int r) {if(l == r) return -1;std::cout << "? " << l << ' ' << r << '\n';std::cout.flush();int pos;std::cin >> pos;return pos;
}void init() {pow2[0] = 1; for(int i = 1; i <= 20; i ++) {pow2[i] = pow2[i - 1] * 2;}
}signed main() {init();std::cin >> n;int l = 1, r = n;int p = ask(l, r);if(ask(1, p) == p) {for(int i = 18; i >= 0; i --) {if(pow2[i] + l <= p && ask(l + pow2[i], p) == p)l += pow2[i];}std::cout << "! " << l << '\n';}else {for(int i = 18; i >= 0; i --) {if(r - pow2[i] >= p && ask(p, r - pow2[i]) == p)r -= pow2[i];}std::cout << "! " << r << '\n';}std::cout.flush();return 0;
}D. Max Median

给出一个数组,要求找到长度至少为k,中间数最大的序列,输出最大的中间数的值。
思路:可以考虑二分答案。在值域上二分,对于每个mid,判断序列中是否存在长度为至少为k的子序列中位数为mid。可以这样处理check函数:遍历数组,大于等于mid的为1,小于mid的为-1,处理前缀和和前缀最小值。处理前缀最小值的原因是这样可以不局限于长度为k的子序列,长度大于等于k的子序列只要有满足条件的都会被找到。
AC Code:
#include <bits/stdc++.h>typedef long long ll;
const int N = 2e5 + 5;
int n, k;
int a[N], pre[N];bool check(int mid) {int sum = 0;for(int i = 1; i <= n; i ++) {if(a[i] >= mid)sum ++;elsesum --;pre[i] = std::min(pre[i - 1], sum);if(i >= k && sum - pre[i - k] > 0)return true;}return false;
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::cin >> n >> k;for(int i = 1; i <= n; i ++) {std::cin >> a[i];}int l = 1, r = n;while(l < r) {int mid = l + r + 1 >> 1;if(check(mid)) l = mid;else r = mid - 1;}std::cout << l << '\n';return 0;
}相关文章:

Codeforces Round 703 (Div. 2)(A~D)
A. Shifting Stacks给出一个数组,每次可以将一个位置-1,右侧相邻位置1,判断是否可以经过若干次操作后使得数列严格递增。思路:对于每个位置,前缀和必须都大于该位置应该有的最少数字,即第一个位置最少是0&a…...

Django项目5——基于tensorflow serving部署深度模型——windows版本
1:安装docker for windows 可能需要安装WLS2,用于支持Linux系统,参照上面的教程安装 2:在Powershell下使用docker docker pull tensorflow/serving3:在Powershell下启动tensorflow serving docker run -p 8500:8500 …...
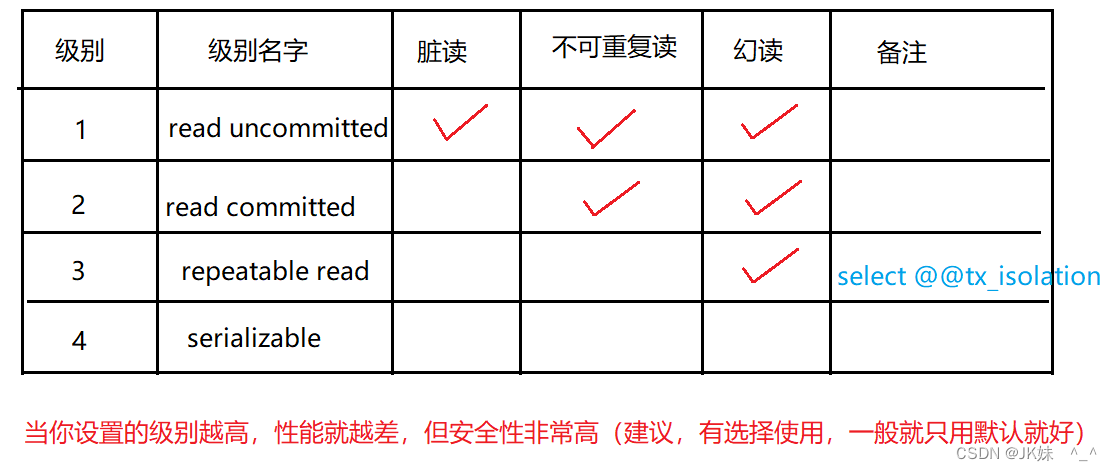
MySQL基础篇3
第一章 多表关系实战 1.1 实战1:省和市 方案1:多张表,一对多 方案2:一张表,自关联一对多 id1 name‘北京’ p_id null; id2 name‘昌平’ p_id1 id3 name‘大兴’ p_id1 id3 name‘上海’ p_idnull id4 name‘浦东’…...
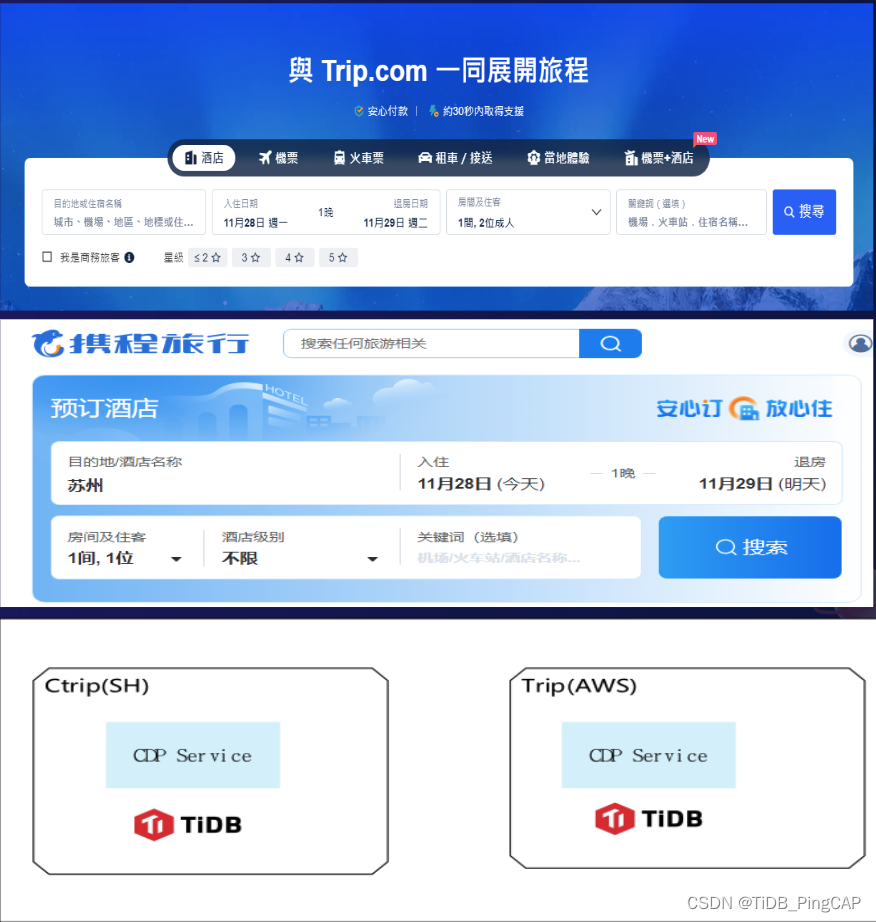
携程 x TiDB丨应对全球业务海量数据增长,一栈式 HTAP 实现架构革新
随着新冠病毒疫情的缓解和控制,全球旅游业逐渐开始重新复苏。尤其在一些度假胜地,游客数量已经恢复到疫情前的水平。 携程作为全球领先的一站式旅行平台,旗下拥有携程旅行网、去哪儿网、Skyscanner 等品牌。携程旅行网向超过 9000 万会员提供…...

记一次Kafka warning排查过程
1、前因 在配合测试某个需求的时候,正好看到控制台打印了个报错,如下: 2023-03-06 17:05:58,565[325651ms][pool-28-thread-1][org.apache.kafka.common.utils.AppInfoParser][WARN] - Error registering AppInfo mbean javax.management.I…...
)
MySQL学习笔记(6.视图)
1. 视图作用 (1). 简化业务,将多个复杂条件,改为视图 (2). mysql对用户授权,只能控制表权限,通过视图可以控制用户字段权限。 (3). 可以避免基本表变更,影响业务。只需更改视图即可。 2. 视图(创建&…...

java多线程与线程池-01多线程知识复习
多线程知识复习 文章目录 多线程知识复习第1章 多线程基础1.1.2 线程与进程的关系1.2 多线程启动1.2.1 线程标识1.2.2 Thread与Runnable1.2.3 run()与start()1.2.4 Thread源码分析1.3 线程状态1.3.1 NEW状态1.3.2 RUNNABLE状态1.3.3 BLOCKED状态1.3.4 WAITING状态1…...

Typescript - 将命名空间A导入另一个命名空间B作为B的子命名空间,并全局暴露命名空间B
前言 最近相统一管理 ts 中的类型声明,这就需要将各模块下的命名空间整合到全局的命名空间下,牵涉到从别的文件中引入命名空间并作为子命名空间在全局命名空间中统一暴露。 将命名空间A导入另一个命名空间B作为B的子命名空间 文件说明 assets.ts 文件中…...
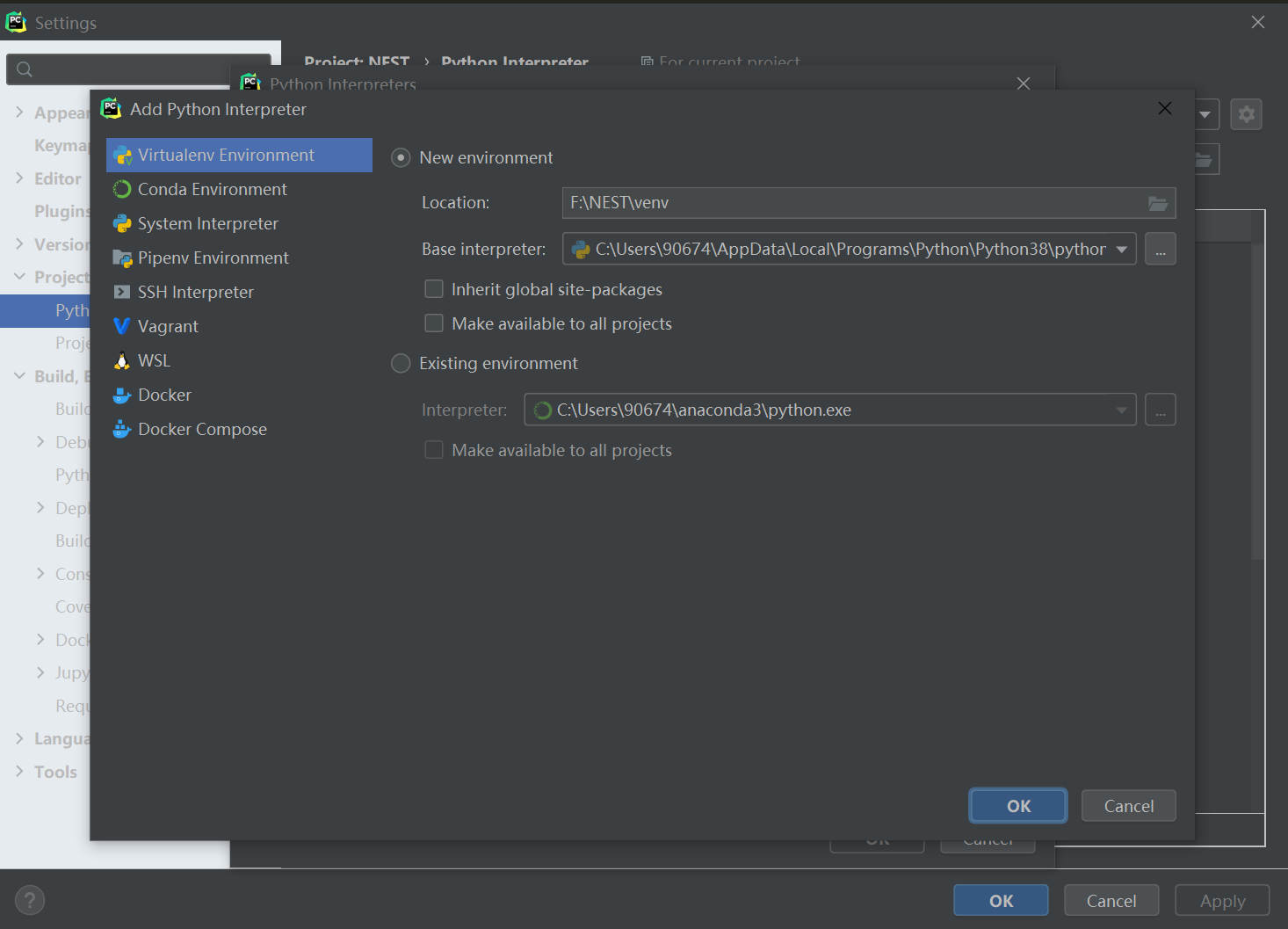
Windows下实现Linux内核的Python开发(WSL2+Conda+Pycharm)
许多软件可以通过Python交互,但没有开发Windows版本,这个时候装双系统或虚拟机都很不方便,可以采取WSL2CondaPycharm的策略来进行基于Linux内核的Python开发。启动WSL2,安装Linux内核教程:旧版 WSL 的手动安装步骤 | M…...

新闻发布网站分析及适用场景
在当今数字时代,发布新闻的渠道已经不再局限于传统媒体,越来越多的企业、组织和个人开始使用互联网平台发布新闻稿,以提升品牌知名度和影响力。本文将介绍一些可以发布新闻的网站,并分析其特点和适用场景。一、新闻稿发布平台1.新…...
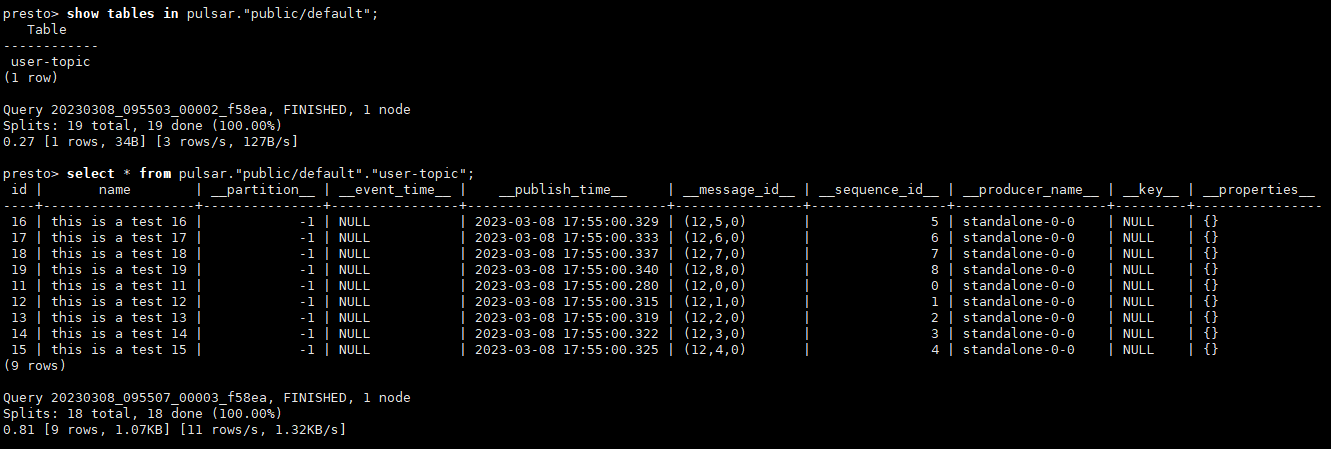
云原生时代顶流消息中间件Apache Pulsar部署实操之Pulsar IO与Pulsar SQL
文章目录Pulsar IO (Connector连接器)基础定义安装Pulsar和内置连接器连接Pulsar到Cassandra安装cassandra集群配置Cassandra接收器创建Cassandra Sink验证Cassandra Sink结果删除Cassandra Sink连接Pulsar到PostgreSQL安装PostgreSQL集群配置JDBC接收器创建JDBC Sink验证JDBC …...
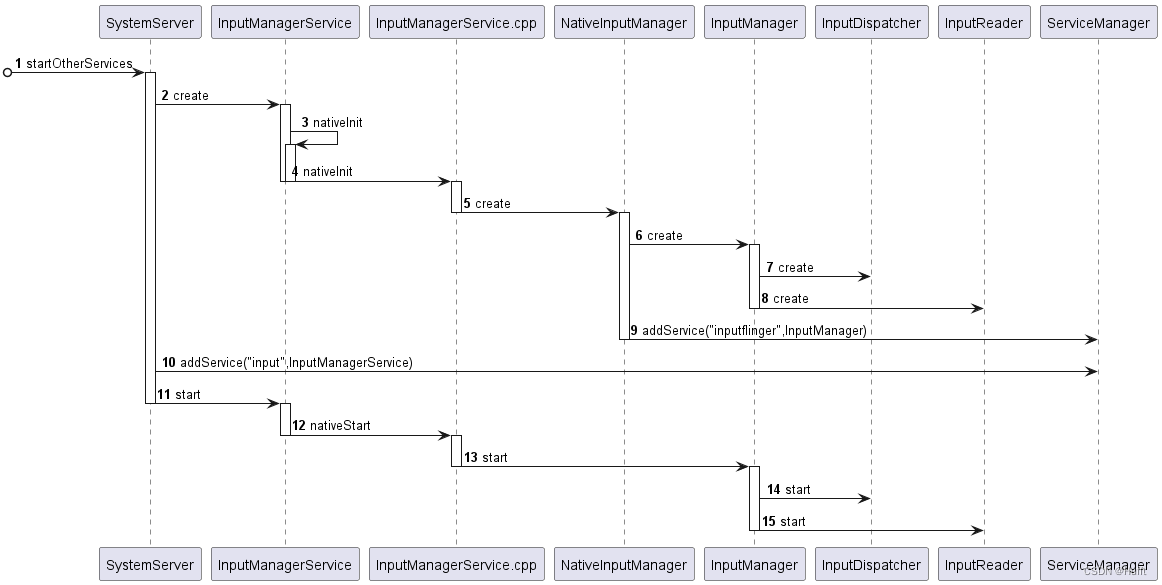
Input子系统(一)启动篇
代码路径 基于AndroidS(12.0)代码 system/core/libutils/Threads.cppframeworks/base/services- java/com/android/server/SystemServer.java- core- java/com/android/server/input/InputManagerService.java- jni/com_android_server_input_InputMan…...

WuThreat身份安全云-TVD每日漏洞情报-2023-03-08
漏洞名称:Agilebio Lab Collector 远程命令执行 漏洞级别:高危 漏洞编号:CVE-2023-24217,CNNVD-202303-375 相关涉及:Agilebio Lab Collector 4.234 漏洞状态:EXP 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-05536 漏洞名称:PrestaShop “Xen Forum”模…...

ABP IStringLocalizer部分场景不生效的问题
问题描述: 本地项目依赖注入本地化服务时候生效,第三方项目调用本地接口时候出现本地化失效的问题。 解决方案: 第三方服务封装的 GetHttp 请求的请求头中添加 语言相关信息 request.Headers.Add("accept-language", "zh-C…...

数组(四)-- LC[167] 两数之和-有序数组
1 两数之和 1.1 题目描述 题目链接:https://leetcode.cn/problems/two-sum/description/ 1.2 求解思路 1. 暴力枚举 最容易想到的方法是枚举数组中的每一个数 x,寻找数组中是否存在 target - x 参考代码 class Solution(object):def twoSum(self, n…...
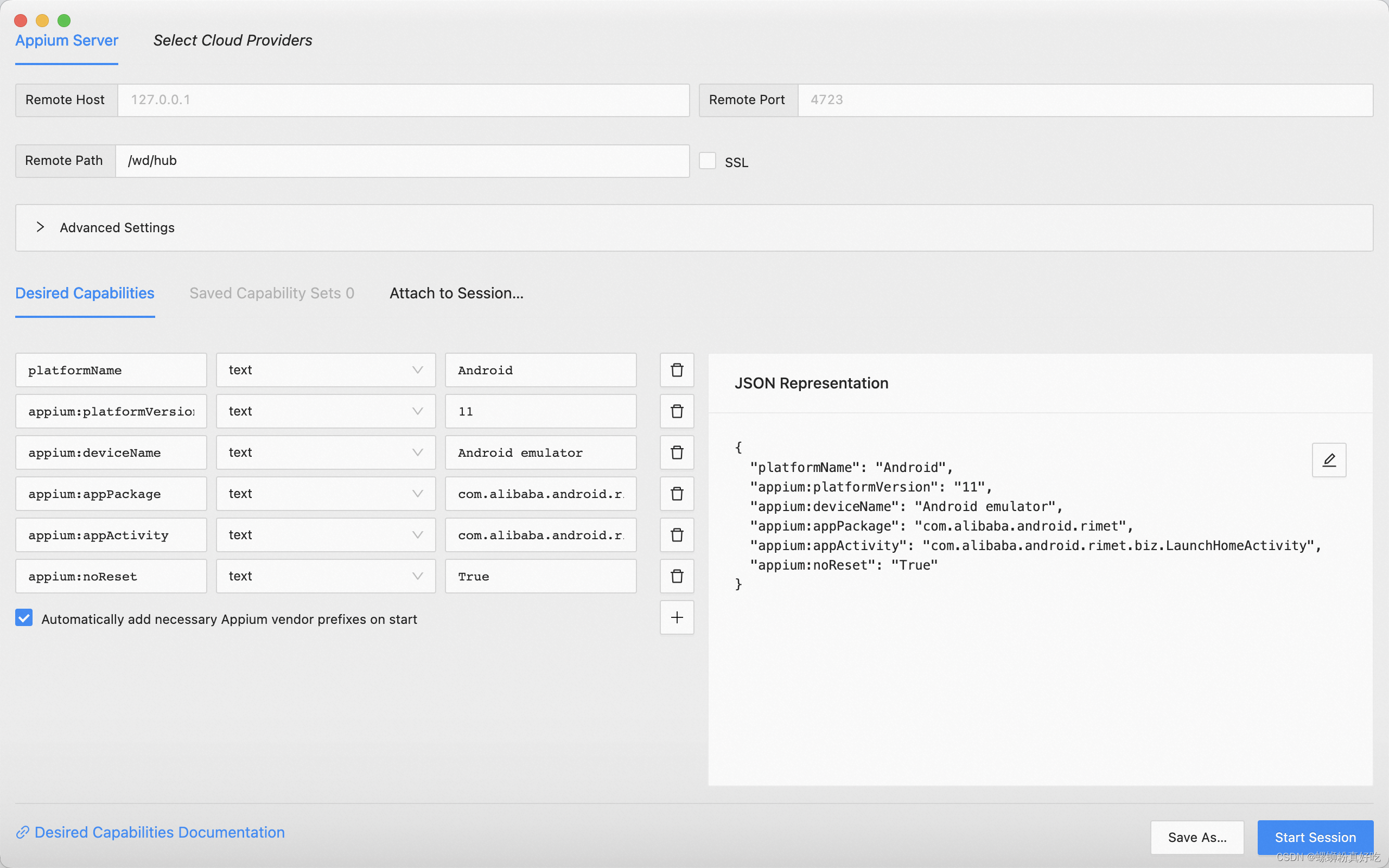
Mac电脑,python+appium+安卓模拟器使用步骤
1、第一步,环境搭建,参考这位博主的文章,很齐全 https://blog.csdn.net/qq_44757414/article/details/128142859 我在最后一步安装appium-doctor的时候,提示权限不足,换成sudo appium-doctor即可 2、第二步࿰…...

Linux命令·find进阶
find是我们很常用的一个Linux命令,但是我们一般查找出来的并不仅仅是看看而已,还会有进一步的操作,这个时候exec的作用就显现出来了。 exec解释:-exec 参数后面跟的是command命令,它的终止是以;为结束标志的࿰…...

R语言ggplot2 | 用百分比格式表示数值
📋文章目录Percent() 函数介绍例子1,在向量中格式化百分比:例子2,格式化数据框列中的百分比:例子3,格式化多个数据框列中的百分比:如何使用percent()函数在绘图过程展示通常在绘图时,…...

【代码训练营】day53 | 1143.最长公共子序列 1035.不相交的线 53. 最大子序和
所用代码 java 最长公告子序列 LeetCode 1143 题目链接:最长公告子序列 LeetCode 1143 - 中等 思路 这个相等于上一题的不连续状态 dp[i] [j]:以[0, i-1]text1和以[0, j-1]text2 的最长公共子序列的长度为dp[i] [j]递推公式: 相同&#x…...
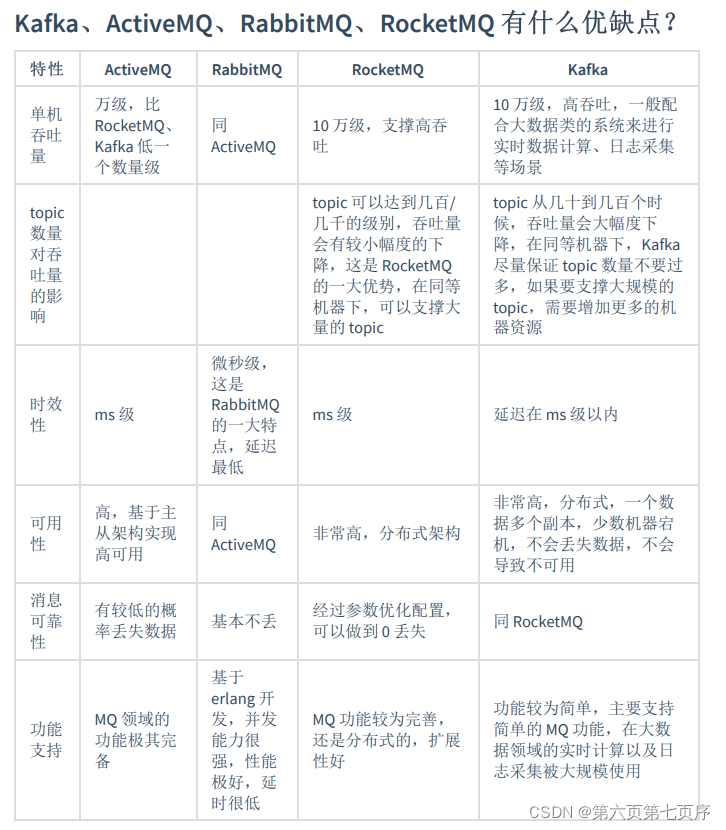
消息队列理解
为什么使用消息队列 使⽤消息队列主要是为了: 减少响应所需时间和削峰。降低系统耦合性(解耦/提升系统可扩展性)。 当我们不使⽤消息队列的时候,所有的⽤户的请求会直接落到服务器,然后通过数据库或者 缓存响应。假…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
