企业或者个体户为什么会经营异常?
在复杂多变的市场经济环境中,无论是企业还是个体工商户,都可能遭遇经营异常的情况。及时识别这些预警信号并采取有效措施,对于避免潜在风险、保持健康发展至关重要。本文将深入探讨企业与个体户常见的经营异常类型、识别方法以及应对策略,并在文末简要介绍我们提供的专业数据定制服务,如何帮助制定科学决策。
1. 经营异常的常见类型
-
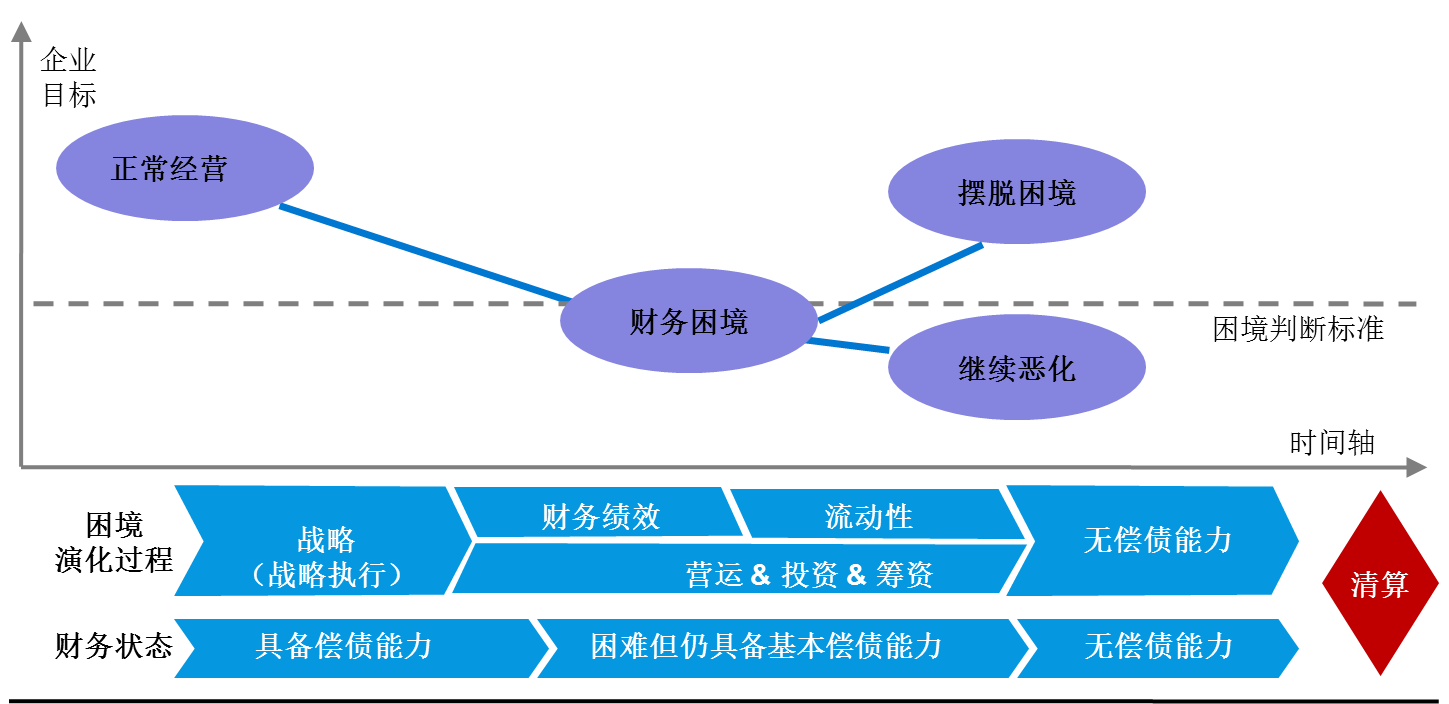
财务困境:现金流紧张、负债率高、连续亏损等。
-
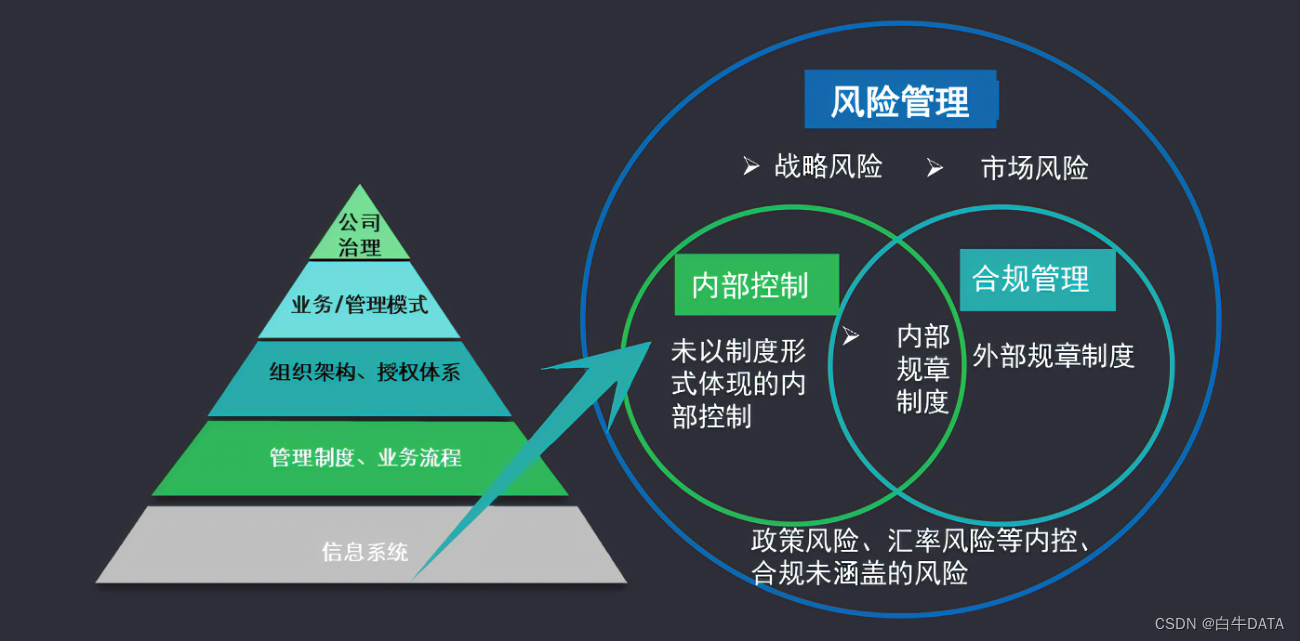
合规问题:税务违规、环保不达标、资质证书过期。

-
市场响应迟缓:产品过时、市场需求变化快、竞争加剧。
-
管理混乱:内部沟通不畅、决策效率低、人才流失。

-
客户关系恶化:投诉增多、客户满意度下降、市场份额减少。
2. 预警信号识别
-
财务指标异常:关注利润率、库存周转率、应收账款周期等指标的异常波动。
-
法律诉讼与负面新闻:频繁的法律纠纷、媒体负面报道可能预示着合规或声誉风险。
-
员工动态:高离职率、招聘困难可能反映内部管理问题。
-
市场反馈:销售下滑、顾客评价骤降需警惕市场需求变化。
-
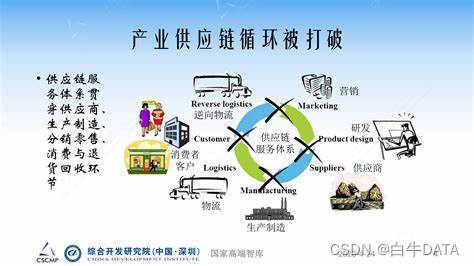
供应链不稳定:供应商延迟交货、质量下降可能影响正常运营。
3. 应对策略
-
加强财务管理:建立严格的预算控制体系,优化成本结构,保持健康的现金流。

-
合规自查与培训:定期进行内部审计,确保各项业务操作符合法律法规要求。
-
市场敏锐性:增强市场研究,快速调整产品策略,紧跟消费者需求变化。
-
内部管理优化:提升组织效能,加强团队建设,促进有效沟通。
-
客户关系管理:积极解决客户投诉,建立长期的客户忠诚计划。
面对经营中的种种挑战,我们作为领先的企业数据定制服务商,打造了用户友好的在线营销线索查询平台,支持多种查询条件筛选,界面直观,操作便捷。无论您是需要批量导出数据,还是希望通过API接口集成至内部系统,我们都提供了灵活多样的访问方式。我们拥有庞大的企业信息数据库,涵盖了国内数百万家企业基本信息、财务报告、经营动态、行业分析、供应链信息、司法风险、知识产权等多个维度,确保您获取的数据全面且深入。立即联系我们,开启您的智慧经营之旅!
相关文章:

企业或者个体户为什么会经营异常?
在复杂多变的市场经济环境中,无论是企业还是个体工商户,都可能遭遇经营异常的情况。及时识别这些预警信号并采取有效措施,对于避免潜在风险、保持健康发展至关重要。本文将深入探讨企业与个体户常见的经营异常类型、识别方法以及应对策略&…...

ROS从入门到精通4-3:制作Docker镜像文件Dockerfile
目录 0 专栏介绍1 为什么需要Dockerfile?2 Dockerfile书写原则3 Dockerfile常用指令3.1 FROM3.2 MAINTAINER3.3 RUN3.4 ADD3.5 COPY3.6 CMD3.7 ENV3.8 EXPOSE3.9 WORKDIR3.10 ARG 4 Dockerfile构建ROS工程实例 0 专栏介绍 本专栏旨在通过对ROS的系统学习࿰…...

【CV】计算机视觉是什么?
计算机视觉是一门研究如何使机器“看”的学科,旨在实现从图像或视频中获取信息的技术和方法。它涵盖了图像处理、模式识别、机器学习等多个领域,是人工智能领域的重要分支之一。以下是计算机视觉的一般概要介绍: 概要介绍: 图像…...

如何在Vue中实现鼠标悬浮展示与隐藏弹窗的功能
如果你需要鼠标在元素和弹窗上时保持弹窗显示,而鼠标离开这两者时隐藏弹窗,你可以使用一个稍微复杂的逻辑来处理鼠标的进入和离开事件。 这通常涉及到延时关闭弹窗,以便给用户足够的时间从元素移动到弹窗上,而不触发弹窗关闭。以…...
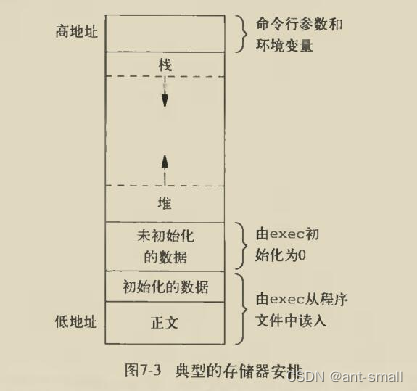
03 Linux编程-进程
1、进程的相关概念 1.1 程序与进程 程序是静态的概念,进程是程序的一次运行活动。 1.2 查看系统中有哪些进程 ps #只显示一小部分进程 ps -aux #会打印当前所有进程 ps -aux|grep init #使用grep筛选出只含有init的进程top #运行显示的进程有点类似windows…...
Hbuild-X运行ios基座app
一、说明 ios真机第一次运行的时候需要下载插件,这个都是自动监测,自动下载的,不用多说。ios真机运行是需要签名的,不然就会报以下错误。如何制作免费的签名证书呢,需要借助爱思助手来完成。 二、安装爱思助手 &…...

Node.js基础:从入门到实战
初识 Node.js 与内置模块 (初识) 1、知道什么是node.js 2、知道node.js可以做什么 3、node.js 中js的组成部分 (内置模块) 4、用 fs 模块读写操作文件 5、使用 path 模块处理路径 6、使用http 模块写一个基本的web服务器 初识 N…...

考研408笔记总结~
目录 一.数据结构 二.计算机组成原理 三.操作系统 四.计算机网络 私以为边看视频,边做笔记会更专注些,大家需要自取。欢迎大家和我一起探讨考研的问题,包括不仅限于专业课,数学,英语等等......,想说什么…...

使用在线工具等方式下载推特视频
使用在线工具等方式下载推特视频 使用在线工具 Visit a Twitter video downloader website: Websites like twdown.net, twittervideodownloader.com, and savevideo.me offer services to download Twitter videos.Paste the Twitter video URL into the designated input bo…...

性能优化:几方面考虑
我们可以继续再考虑下关于性能优化,我们还能从哪些方面着手呢? 1. 代码层面: 使用更高效的数据结构和算法。使用缓存避免多次数据库交互减少不必要的计算和内存分配。利用并行和异步编程提高性能。使用性能分析工具定位和优化瓶颈。 2. We…...

学习大数据:论学习Spark的重要性
随着科技的不断发展,大数据已经成为了当今社会的热门话题。大数据技术的出现,为我们提供了处理海量数据的新方法,使得我们能够从这些数据中挖掘出有价值的信息。在众多的大数据处理框架中,Apache Spark无疑是最为出色的一种。本文…...

学习java第七十一天
DI:依赖注入 依赖注入是spring容器中创建对象时给其设置依赖对象的方式,比如给spring一个清单,清单中列出了需要创建B对象以及其他的一些对象(可能包含了B类型中需要依赖对象),此时spring在创建B对象的时候…...

Altium Designer PCB快捷键设置
6)PCB修改快捷键,并自定义工具栏 添加boardlayerset系统命令。 修改系统脚本, 在D:\Program Files\Altium\AD18\System下,找到advpcb.rcs文件,打开。 Tree MNPCB_LayerSets CaptionManage Layer Se&ts Popup Emp…...
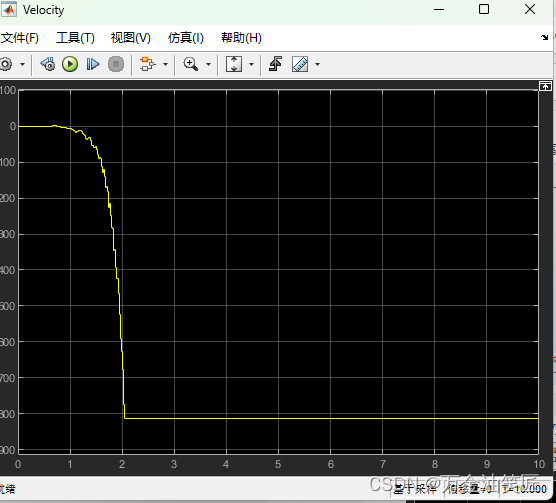
玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真(案例实战)
** 玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真(案例实战) ** 目录 玩转Matlab-Simscape(初级)- 08 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真&…...
vue嵌套路由
一、嵌套 children配置 1.父类路由 mymusic 2.子类路由 musicson 1.创建MusicSon组件 <template><div><p>从前和后来</p><p>唯一</p><p>运气来的似有若无</p></div> </template><script>export defaul…...
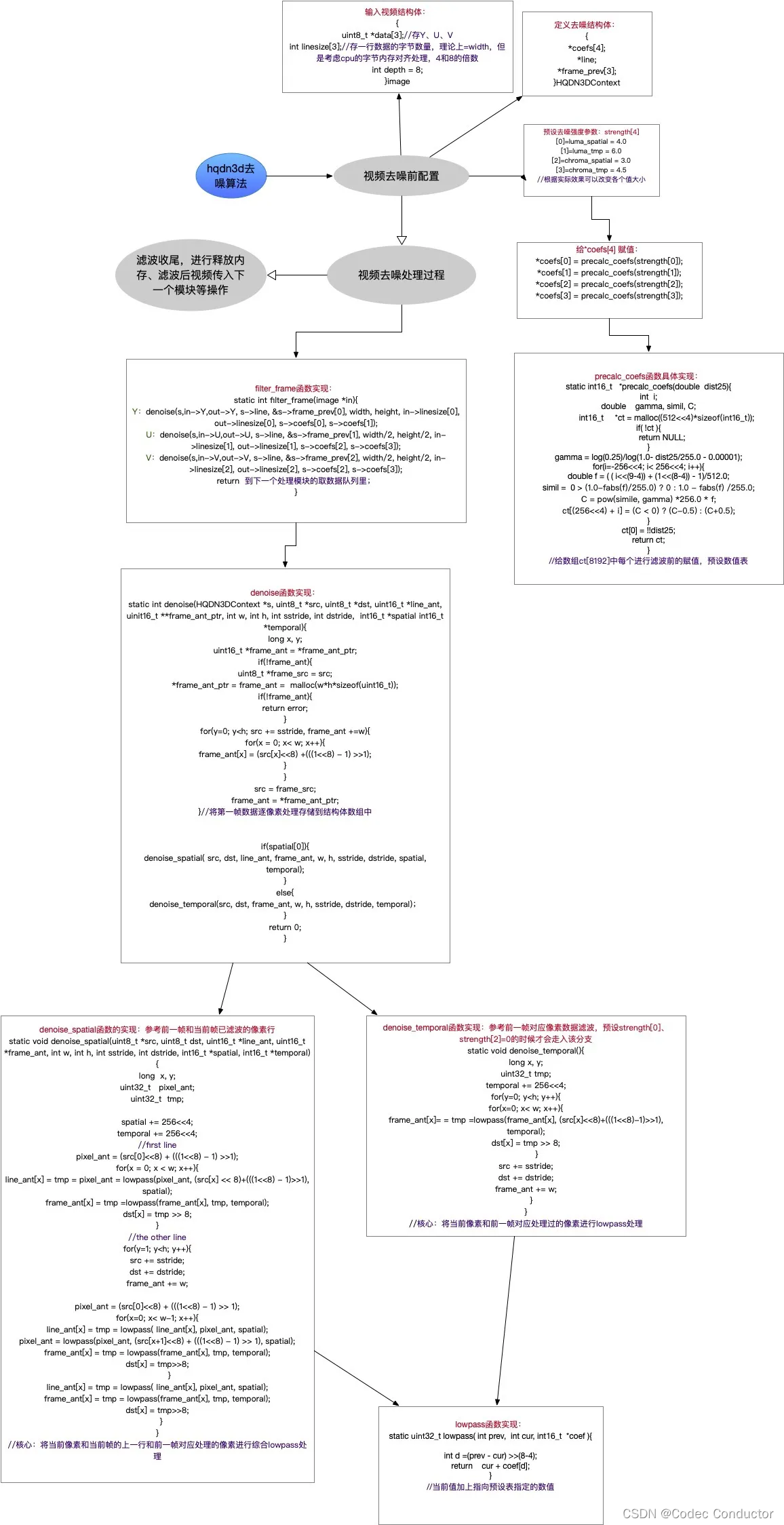
视频降噪算法 hqdn3d 原理分析
视频降噪 视频降噪是一种处理技术,旨在减少视频中的噪声,提高画面质量。噪声可能来自多种源头,包括摄像机的传感器、压缩算法、传输过程中的干扰等。降噪处理对于视频监控、视频会议、电影后期制作以及任何需要高画质输出的应用场景都非常重…...
Ansys Mechanical|屈曲分析技术
屈曲分析的基本概念 当受拉杆件的应力达到屈服极限或强度极限时,将引起塑性变形或断裂。这些是由于强度不足所引起的失效。 在工程中,我们会注意到当细长杆件受压时,表现出与强度失效完全不同的性质。当杆件受压超过某一临界值时࿰…...

【大模型微调】一文掌握7种大模型微调的方法
本篇文章深入分析了大型模型微调的基本理念和多样化技术,细致介绍了LoRA、适配器调整(Adapter Tuning)、前缀调整(Prefix Tuning)等多个微调方法。详细讨论了每一种策略的基本原则、主要优点以及适宜应用场景,使得读者可以依据特定的应用要求和计算资源限…...

MySQL表突然卡死,删、查操作加载不停解决办法
今天遇到了MySQL删表的时候卡死情况。然后通过网上查阅资料和项目组沟通,了解到了有多人同时对同一张表进行了操作。我和另一个同事同时进行了删除操作,然后另两位同时进行了查询操作,然后还有一位同事用dolphin调度,用datax采集数…...

Rust 标准库的结构及其模块路径
在 Rust 中,标准库提供了一组核心功能,以帮助开发者执行常见的编程任务。当使用这些功能时,我们需要通过特定的模块路径来引用它们。下面,我们将详细介绍 Rust 标准库的结构,并提供相应的 use 路径。 Rust 标准库模块…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
