【机器学习与实现】支持向量机SVM
目录
- 一、SVM (Support Vector Machine) 概述
- (一)支持向量机SVM的主要特点
- (二)支持向量与间隔最大化
- (三)线性可分/不可分
- (四)软间隔 (soft margin) 与核技巧 (kernel trick)
- (五)核技巧配合软间隔解决线性不可分问题
- 二、硬间隔解决线性可分问题
- (一)线性可分的决策超平面
- (二)硬间隔、决策边界和支持向量之间关系
- (三)最大化间隔宽度
- (四)最小化损失函数及其求解方法
- (五)带不等式约束的优化问题的解与KKT条件
- (六)拉格朗日对偶问题及其求解
- 三、软间隔解决线性不可分问题
- (一)软间隔SVM分类器的核心思想
- (二)软间隔SVM分类器的损失函数
- (三)核技巧使用映射函数升维解决分类问题
- (四)软间隔+核技巧的SVM优化问题
- (五)拉格朗日对偶问题与核函数
- (六)常见的核函数
- 四、scikit-learn中的SVM分类器及其主要参数
- (一)多分类的情形
- (二)SVM的属性和方法
- 五、支持向量机应用示例
一、SVM (Support Vector Machine) 概述
(一)支持向量机SVM的主要特点
- 支持向量机 SVM 是一种既可以用于分类、也可以用于回归问题的监督学习算法。
- SVM 的主要思想是找到一个具有最大间隔 (max margin) 的分类决策超平面,从而可以将不同类别的样本点分隔开。
- SVM 是一个非常强大的算法,因为它使用内积核函数将原始输入数据映射到高维空间,从而能够处理高维空间和非线性问题,并且能够有效地避免过拟合。
- SVM 的缺点是它对于大型数据集的计算成本很高,以及内积核函数的选择和调整需要一定的经验和技巧。
(二)支持向量与间隔最大化

图中深蓝色线便是决策边界,也称分离超平面;两条虚线之间宽度叫做间隔 (margin)。支持向量机的优化目标为——间隔最大化。
支持向量(红蓝加圈的点)确定决策边界位置;而其他数据并没有对决策起到任何作用。因此,SVM 对于数据特征数量远高于数据样本量的情况也有效(可以处理高维数据)。
(三)线性可分/不可分

- 线性可分问题采用硬间隔 (hard margin);即间隔内没有数据点。
- 支持向量机解决线性不可分问题,需要并用软间隔和核技巧。
(四)软间隔 (soft margin) 与核技巧 (kernel trick)

- 软间隔相当于一个缓冲区。使用软间隔分类时,允许有数据点侵入间隔,甚至超越间隔带。
- 核技巧将数据映射到高维特征空间,是一种数据升维。
(五)核技巧配合软间隔解决线性不可分问题

二、硬间隔解决线性可分问题
(一)线性可分的决策超平面
1、决策超平面定义
决策超平面定义为: f ( x ) = w T x + b = 0 f(x)=w^Tx+b=0 f(x)=wTx+b=0,其中 w w w 是超平面的法向量

接下来我们的目标是研究不同类别的支持向量间的间距如何用系数向量 w w w 和 b b b 表示出来。只要能表示出来这个间距,通过间距最大化就可能求出系数向量 w w w 和 b b b,这样就得到了决策面。
2、平面外一点到平面的距离

-
设 x x x 是平面上任一点, q q q 是平面外任一点,向量 a a a 是两者的连线,则有: a = q − x , w T + b = 0 a=q-x, w^T+b=0 a=q−x,wT+b=0
-
设向量 a a a 在法向量 w w w 方向的投影向量 d d d 的长度为 D D D,则 D = ∣ w T a ∣ ∣ ∣ w ∣ ∣ = ∣ w T ( q − x ) ∣ ∣ ∣ w ∣ ∣ = ∣ w T q + b ∣ ∣ ∣ w ∣ ∣ \begin{aligned}D=\frac{|w^Ta|}{||w||}=\frac{|w^T(q-x)|}{||w||}=\frac{|w^Tq+b|}{||w||}\end{aligned} D=∣∣w∣∣∣wTa∣=∣∣w∣∣∣wT(q−x)∣=∣∣w∣∣∣wTq+b∣
-
一般情况下距离不考虑正负。但是,对于分类问题,考虑距离正负便于判断点和超平面关系,因此去掉分子的绝对值符号,用 D > 0 D>0 D>0 表示 q q q 在平面上方;反之 D < 0 D<0 D<0 表示 q q q 在平面下方。
(二)硬间隔、决策边界和支持向量之间关系

-
硬间隔的下边界为 l 1 l_1 l1 , l 1 l_1 l1 到决策边界距离为 − h -h −h。而支持向量 C 在 l 1 l_1 l1 上,则有: w T x + b ∣ ∣ w ∣ ∣ = − h \begin{aligned}\frac{w^Tx+b}{||w||}=-h\end{aligned} ∣∣w∣∣wTx+b=−h
-
硬间隔的上边界为 l 2 l_2 l2, l 2 l_2 l2 到决策边界距离为 + h +h +h。而支持向量 A、B 在 l 2 l_2 l2 上,则有: w T x + b ∣ ∣ w ∣ ∣ = + h \begin{aligned}\frac{w^Tx+b}{||w||}=+h\end{aligned} ∣∣w∣∣wTx+b=+h
-
距离决策边界大于等于 + h +h +h 的样本点,标记为 y = + 1 y=+1 y=+1;距离决策边界小于等于 − h -h −h 的样本点,标记为 y = − 1 y=-1 y=−1,则有:
{ w T x + b ∣ ∣ w ∣ ∣ ≥ + h , y = + 1 w T x + b ∣ ∣ w ∣ ∣ ≤ − h , y = − 1 ⇒ ( w T x + b ) y ∣ ∣ w ∣ ∣ h ≥ 1 \left\{ \begin{array}{l} \begin{aligned}\frac{w^Tx+b}{||w||}≥+h,y=+1\end{aligned}\\[3ex] \begin{aligned}\frac{w^Tx+b}{||w||}≤-h,y=-1\end{aligned} \end{array} \right. \Rightarrow \frac{(w^Tx+b)y}{||w||h}≥1 ⎩ ⎨ ⎧∣∣w∣∣wTx+b≥+h,y=+1∣∣w∣∣wTx+b≤−h,y=−1⇒∣∣w∣∣h(wTx+b)y≥1
(三)最大化间隔宽度
为简化计算,令分母 ∣ ∣ w ∣ ∣ h = 1 ||w||h=1 ∣∣w∣∣h=1,则间隔上下边界的解析式变为:
{ w T x + b = + 1 w T x + b = − 1 \left\{ \begin{array}{l} w^Tx+b=+1 \\[1ex] w^Tx+b=-1 \end{array} \right. {wTx+b=+1wTx+b=−1
则间隔宽度 2 h = 2 ∣ ∣ w ∣ ∣ 2h=\frac{2}{||w||} 2h=∣∣w∣∣2,最大化间隔宽度可表示为
arg max w , b 2 ∣ ∣ w ∣ ∣ s u b j e c t t o ( x ( i ) w + b ) y ( i ) ≥ 1 , i = 1 , 2 , 3 , . . . , n \begin{aligned} &\argmax_{w,b} \frac{2}{||w||}\\[3ex] &subject \ to \ (x^{(i)}w+b)y^{(i)}≥1,i=1,2,3,...,n \end{aligned} w,bargmax∣∣w∣∣2subject to (x(i)w+b)y(i)≥1,i=1,2,3,...,n
(四)最小化损失函数及其求解方法
最大化间隔宽度等价于求解下列带不等式约束的最小化问题:
arg min w , b ∣ ∣ w ∣ ∣ 2 2 = w T w 2 = w ⋅ w 2 s u b j e c t t o ( x ( i ) w + b ) y ( i ) ≥ 1 , i = 1 , 2 , 3 , . . . , n (a)式 \begin{aligned} &\argmin_{w,b} \frac{||w||^2}{2}=\frac{w^Tw}{2}=\frac{w\cdot w}{2}\tag*{(a)式}\\[3ex] &subject \ to \ (x^{(i)}w+b)y^{(i)}≥1,i=1,2,3,...,n \end{aligned} w,bargmin2∣∣w∣∣2=2wTw=2w⋅wsubject to (x(i)w+b)y(i)≥1,i=1,2,3,...,n(a)式
-
求解方法1:因为 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2 是严格的凸函数,所以该问题属于经典的凸优化问题,可以用 QP (二次规划) 算法求解。
-
求解方法2:通过拉格朗日乘子法,把上述带约束的最小化问题转化成无约束的最小化问题:
L ( w , b , λ ) = w ⋅ w 2 + ∑ i = 1 n λ i ( 1 − y ( i ) ( x ( i ) w + b ) ) (b)式 L(w,b,\lambda)=\frac{w\cdot w}{2}+\sum_{i=1}^n\lambda_i(1-y^{(i)}(x^{(i)}w+b))\tag*{(b)式} L(w,b,λ)=2w⋅w+i=1∑nλi(1−y(i)(x(i)w+b))(b)式 其中, λ = [ λ 1 λ 2 ⋯ λ n ] T \lambda=\left[\begin{matrix}\lambda_1 \ \lambda_2 \ \cdots \ \lambda_n\end{matrix} \right]^T λ=[λ1 λ2 ⋯ λn]T
(五)带不等式约束的优化问题的解与KKT条件
根据优化理论,上述(a)式子存在最优解的充要条件是满足如下KKT条件:
K T T 条件 { ∂ L ( w , b , λ ) ∂ w = 0 , ∂ L ( w , b , λ ) ∂ b = 0 , 其中 L ( w , b , λ ) 是前面的 ( b ) 式 λ i ≥ 0 g i ( w , b ) = 1 − y ( i ) ( w T x ( i ) + b ) ≤ 0 , i = 1 , 2 , . . . , n λ i g i ( w , b ) = 0 KTT条件 \left\{ \begin{array}{l} \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial w}=0, \ \frac{\partial L(w,b,\lambda)}{\partial b}=0, \ 其中L(w,b,\lambda)是前面的(b)式\end{aligned}\\[1ex] \begin{aligned}\lambda_i≥0 \end{aligned}\\[1ex] \begin{aligned}g_i(w,b)=1-y^{(i)}(w^Tx^{(i)}+b)≤0, \ i=1,2,...,n\end{aligned}\\[1ex] \lambda_ig_i(w,b)=0 \end{array} \right. KTT条件⎩ ⎨ ⎧∂w∂L(w,b,λ)=0, ∂b∂L(w,b,λ)=0, 其中L(w,b,λ)是前面的(b)式λi≥0gi(w,b)=1−y(i)(wTx(i)+b)≤0, i=1,2,...,nλigi(w,b)=0
上面第4式 λ i g i ( w , b ) = 0 \lambda_ig_i(w,b)=0 λigi(w,b)=0 也称为互补条件,它表示:若 λ i > 0 \lambda_i>0 λi>0,则 1 − y ( i ) ( w T x ( i ) + b ) = 0 1-y^{(i)}(w^Tx^{(i)}+b)=0 1−y(i)(wTx(i)+b)=0,即对应的样本点 x ( i ) x^{(i)} x(i) 一定是落在间隔超平面上的支持向量;若 g i ( w , b ) < 0 g_i(w,b)<0 gi(w,b)<0,即 y ( i ) ( w T x ( i ) + b ) > 1 y^{(i)}(w^Tx^{(i)}+b)>1 y(i)(wTx(i)+b)>1 则一定有 λ i = 0 \lambda_i=0 λi=0,说明非支持向量对应的拉格朗日乘子一定为0。
因为支持向量数量较少,说明大于0的拉格朗日乘子较少,因此拉格朗日向量是一个稀疏向量。
(六)拉格朗日对偶问题及其求解
根据KKT条件第一行的求导式等于0,可得:
{ ∂ L ( w , b , λ ) ∂ w = w − ∑ i = 1 n λ i y ( i ) x ( i ) T = 0 ∂ L ( w , b , λ ) ∂ b = ∑ i = 1 n λ i y ( i ) = 0 ⇒ { w = ∑ i = 1 n λ i y ( i ) x ( i ) T ∑ i = 1 n λ i y ( i ) = 0 (c)式 \left\{ \begin{array}{l} \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial w}=w-\sum_{i=1}^n\lambda_iy^{(i)}x^{(i)T}=0\end{aligned}\\[2ex] \begin{aligned}\frac{\partial L(w,b,\lambda)}{\partial b}=\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \begin{aligned}w=\sum_{i=1}^n\lambda_iy^{(i)}x^{(i)T}\end{aligned}\\[2ex] \begin{aligned}\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned} \end{array} \right.\tag*{(c)式} ⎩ ⎨ ⎧∂w∂L(w,b,λ)=w−i=1∑nλiy(i)x(i)T=0∂b∂L(w,b,λ)=i=1∑nλiy(i)=0⇒⎩ ⎨ ⎧w=i=1∑nλiy(i)x(i)Ti=1∑nλiy(i)=0(c)式
( c ) (c) (c) 式带入前面的 ( b ) (b) (b) 式并消去 w w w 和 b b b 向量,得到只含拉格朗日乘子的损失函数:
L ( λ ) = ∑ i = 1 n λ i − ∑ j = 1 n ∑ i = 1 n λ i λ j y ( i ) y ( j ) ( x ( i ) ⋅ x ( j ) ) 2 (d)式 \begin{aligned} L(\lambda)=\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\left(x^{(i)}\cdot x^{(j)}\right)}{2}\tag*{(d)式} \end{aligned} L(λ)=i=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)(x(i)⋅x(j))(d)式 其中, x ( i ) ⋅ x ( j ) x^{(i)}\cdot x^{(j)} x(i)⋅x(j) 为两个向量的内积。
由此得到拉格朗日对偶问题。该对偶问题可以用 SMO (序列最小化) 算法来高效求解。
arg min λ ∑ i = 1 n λ i − ∑ j = 1 n ∑ i = 1 n λ i λ j y ( i ) y ( j ) ( x ( i ) ⋅ x ( j ) ) 2 s u b j e c t t o { ∑ i = 1 n λ i y ( i ) = 0 λ i ≥ 0 , i , j = 1 , 2 , 3 , . . . , n \begin{aligned} &\argmin_\lambda\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\left(x^{(i)}\cdot x^{(j)}\right)}{2}\\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}\sum_{i=1}^n\lambda_iy^{(i)}=0\end{aligned}\\[1ex] \begin{aligned}\lambda_i≥0, \ \ i,j=1,2,3,...,n\end{aligned} \end{array} \right. \end{aligned} λargmini=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)(x(i)⋅x(j))subject to⎩ ⎨ ⎧i=1∑nλiy(i)=0λi≥0, i,j=1,2,3,...,n
三、软间隔解决线性不可分问题
(一)软间隔SVM分类器的核心思想

软间隔SVM分类器的核心思想是允许一些样本不满足硬间隔约束/条件,即允许对一些样本犯错。
这样做是牺牲部分数据点分类准确性,来换取更宽的间隔,由此降低了模型对噪声点的敏感性,可以避免SVM分类器过拟合,提升了模型的泛化性能。
(二)软间隔SVM分类器的损失函数
arg min w , b , ξ w ⋅ w 2 + C ∑ i = 1 n ξ i s u b j e c t t o { y ( i ) ( x ( i ) w + b ) ≥ 1 − ξ i , i = 1 , 2 , 3 , . . . , n ξ i ≥ 0 \begin{aligned} &\argmin_{w,b,\xi}\frac{w\cdot w}{2}+C\sum_{i=1}^n\xi_i \\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}y^{(i)}\left(x^{(i)}w+b\right)≥1-\xi_i, \ i=1,2,3,...,n\end{aligned}\\[1ex] \begin{aligned}\xi_i≥0\end{aligned} \end{array} \right. \end{aligned} w,b,ξargmin2w⋅w+Ci=1∑nξisubject to⎩ ⎨ ⎧y(i)(x(i)w+b)≥1−ξi, i=1,2,3,...,nξi≥0
软间隔有两个重要参数:
- 松弛变量 (slack variable) ξ \xi ξ,一般读作 /ksaɪ/
- 惩罚因子 (penalty parameter) C
1、松弛变量
松弛变量 ξ \xi ξ 表示样本离群的程度,松弛变量值越大,对应的样本离群越远,松弛变量为零,则对应的样本没有离群。SVM希望各样本点的松弛变量之和 ∑ i = 1 n ξ i \begin{aligned}\sum_{i=1}^n\xi_i\end{aligned} i=1∑nξi 越小越好。
2、惩罚因子
(1)惩罚因子 C 是用户设定的一个大于等于0的超参数
- C决定了你有多重视离群点带来的损失,你定的C越大,对目标函数的损失也越大,此时就暗示着你非常不愿意放弃这些离群点。
- 最极端的情况是你把C定为无限大,这样只要稍有一个点离群,目标函数的值马上变成无限大,马上让问题变成无解,这就退化成了硬间隔问题。
- 较小的C值代表着较高的容错性,此时训练误差可能会大,但泛化误差可能会小。
(2)惩罚因子对软间隔宽度和决策边界的影响

管制宽松(对应C值小),则弹性空间大,容错性高,未来可能发展得更好!
(三)核技巧使用映射函数升维解决分类问题
例1

例2
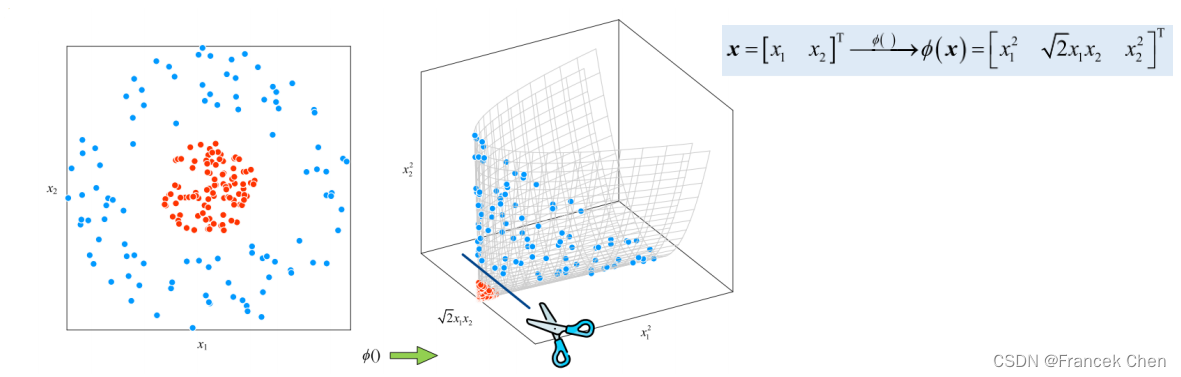
(四)软间隔+核技巧的SVM优化问题
软间隔 + 核技巧的SVM 优化问题的基本思想就是通过最小化如下的损失函数,希望在映射后的高维空间求解一个最优分类超平面:
arg min w , b w ⋅ w 2 + C ∑ i = 1 n ξ i s u b j e c t t o { y ( i ) ( w ⋅ ϕ ( x ( i ) ) + b ) ≥ 1 − ξ i , i = 1 , 2 , 3 , . . . , n ξ i ≥ 0 \begin{aligned} &\argmin_{w,b}\frac{w\cdot w}{2}+C\sum_{i=1}^n\xi_i \\[3ex] &subject \ to \left\{ \begin{array}{l} \begin{aligned}y^{(i)}\left(w\cdot \phi\left(x^{(i)}\right)+b\right)≥1-\xi_i, \ i=1,2,3,...,n\end{aligned}\\[1ex] \begin{aligned}\xi_i≥0\end{aligned} \end{array} \right. \end{aligned} w,bargmin2w⋅w+Ci=1∑nξisubject to⎩ ⎨ ⎧y(i)(w⋅ϕ(x(i))+b)≥1−ξi, i=1,2,3,...,nξi≥0 其中, ϕ ( ) \phi() ϕ() 是映射函数。
(五)拉格朗日对偶问题与核函数
引入映射函数后的无约束拉格朗日对偶问题的形式如下:
L ( w , b , λ ) = w ⋅ w 2 + ∑ i = 1 n λ i ( 1 − y ( i ) ( w ⋅ ϕ ( x ( i ) ) + b ) ) = ∑ i = 1 n λ i − ∑ j = 1 n ∑ i = 1 n λ i λ j y ( i ) y ( j ) ϕ ( x ( i ) ) ⋅ ϕ ( x ( j ) ) ⏞ K e r n e l f u n c t i o n 2 \begin{aligned} L(w,b,\lambda)&=\frac{w\cdot w}{2}+\sum_{i=1}^n\lambda_i\left(1-y^{(i)}\left(w\cdot \phi\left(x^{(i)}\right)+b\right)\right)\\[3ex] &=\sum_{i=1}^n\lambda_i-\frac{\sum_{j=1}^n\sum_{i=1}^n\lambda_i\lambda_jy^{(i)}y^{(j)}\overbrace{\phi\left(x^{(i)}\right)\cdot\phi \left(x^{(j)}\right)}^{Kernel function}}{2} \end{aligned} L(w,b,λ)=2w⋅w+i=1∑nλi(1−y(i)(w⋅ϕ(x(i))+b))=i=1∑nλi−2∑j=1n∑i=1nλiλjy(i)y(j)ϕ(x(i))⋅ϕ(x(j)) Kernelfunction
- 这里出现了两个向量映射到高维空间后的向量内积的形式
- 因为映射函数 ϕ \phi ϕ 是未知的,所以该内积无法直接计算
- 实际通过使用核函数来模拟高维空间的向量内积
核函数一般记为 κ ( x ( i ) , x ( j ) ) \kappa\left(x^{(i)},x^{(j)}\right) κ(x(i),x(j)),并且定义核函数等于高维空间的向量内积:
κ ( x ( i ) , x ( j ) ) = ϕ ( x ( i ) ) ⋅ ϕ ( x ( j ) ) \kappa\left(x^{(i)},x^{(j)}\right)=\phi\left(x^{(i)}\right)\cdot\phi \left(x^{(j)}\right) κ(x(i),x(j))=ϕ(x(i))⋅ϕ(x(j))
(六)常见的核函数
如何选择核函数还没有统一的方法,但可以用常见的四种核函数去尝试分类。其中,线性核是支持向量机 SVM 的标配。
- 线性核 (linear kernel) : κ ( x , q ) = x ⋅ q \begin{aligned}\kappa(x,q)=x\cdot q\end{aligned} κ(x,q)=x⋅q
- 多项式核 (polynomial kernel) : κ p o l y ( d ) ( x , q ) = ( γ x ⋅ q + r ) d \begin{aligned}\kappa_{poly(d)}(x,q)=(\gamma x\cdot q+r)^d\end{aligned} κpoly(d)(x,q)=(γx⋅q+r)d
- 高斯核 (Gaussian kernel),也叫径向基核 RBF (radial basis function kernel) : κ R B F ( x , q ) = exp ( − γ ∣ ∣ x − q ∣ ∣ 2 ) \begin{aligned}\kappa_{RBF}(x,q)=\exp\left(-\gamma||x-q||^2\right)\end{aligned} κRBF(x,q)=exp(−γ∣∣x−q∣∣2)
- Sigmoid 核 (sigmoid kernel) : κ S i g m o i d ( x , q ) = tanh ( γ x ⋅ q + r ) \begin{aligned}\kappa_{Sigmoid}(x,q)=\tanh(\gamma x\cdot q+r)\end{aligned} κSigmoid(x,q)=tanh(γx⋅q+r)
以二次核为例

可以发现 ϕ ( ) \phi() ϕ() 映射规则并不唯一。或者说, ϕ ( ) \phi() ϕ() 的具体形式并不重要,我们关心的是映射规则和标量结果。
四、scikit-learn中的SVM分类器及其主要参数
常用于构建SVM模型的类为SVC,其基本语法格式如下:
class sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr',
random_state=None)

(一)多分类的情形
基本思想是将多分类任务分解为多个二分类任务,对于每一个二分类任务使用一个SVM分类器。

(二)SVM的属性和方法


五、支持向量机应用示例
取自UCI公共测试数据库中的汽车评价数据集作为本例的数据集,该数据集共有6个特征数据,1个分类标签,共1728条记录,部分数据如下表所示。
| a 1 a_1 a1 | a 2 a_2 a2 | a 3 a_3 a3 | a 4 a_4 a4 | a 5 a_5 a5 | a 6 a_6 a6 | d d d |
|---|---|---|---|---|---|---|
| 4 | 4 | 2 | 2 | 3 | 2 | 3 |
| 4 | 4 | 2 | 2 | 3 | 3 | 3 |
| 4 | 4 | 2 | 2 | 3 | 1 | 3 |
| 4 | 4 | 2 | 2 | 2 | 2 | 3 |
| 4 | 4 | 2 | 2 | 2 | 3 | 3 |
| 4 | 4 | 2 | 2 | 2 | 1 | 3 |
| 4 | 4 | 2 | 2 | 1 | 2 | 3 |
| 4 | 4 | 2 | 2 | 1 | 3 | 3 |
| 4 | 4 | 2 | 2 | 1 | 1 | 3 |
| 4 | 4 | 2 | 4 | 3 | 2 | 3 |
| 4 | 4 | 2 | 4 | 3 | 3 | 3 |
| 4 | 4 | 2 | 4 | 3 | 1 | 3 |
注:数据集下载地址为:http://archive.ics.uci.edu/dataset/19/car+evaluation
数据集car.xlsx下载地址:
链接:https://pan.quark.cn/s/5c25b1f7fb08
提取码:z8Q7
其中特征 a 1 a_1 a1 ~ a 6 a_6 a6 的含义及取值依次为:
- Buying (购买价格) :v-high, high, med, low
- maint (维修成本) :v-high, high, med, low
- Doors (车门数量) :2, 3, 4, 5-more
- Persons (载客人数) :2, 4, more
- lug_boot (行李箱大小) :small, med, big
- Safety (安全等级) :low, med, high
分类标签 d d d 的取值情况为:unacc 1, acc 2, good 3, v-good 4
取数据集的前1690条记录作为训练集,余下的作为测试集,计算其预测准确率。其计算流程及思路如下:
1、数据获取
import pandas as pd
data = pd.read_excel('car.xlsx')
2、训练样本与测试样本划分。其中训练用的特征数据用x表示,预测变量用y表示;测试样本则分别记为 x 1 x_1 x1 和 y 1 y_1 y1。
x = data.iloc[:1690,:6].as_matrix()
y = data.iloc[:1690,6].as_matrix()
x1= data.iloc[1691:,:6].as_matrix()
y1= data.iloc[1691:,6].as_matrix()
3、支持向量机分类模型构建
(1)导入支持向量机模块svm。
from sklearn import svm
(2)利用svm创建支持向量机类svm。
clf = svm.SVC(kernel='rbf')
其中核函数可以选择线性核、多项式核、高斯核、sig核,分别用linear,poly,rbf,sigmoid表示,默认情况下选择高斯核。
(3)调用svm中的fit()方法进行训练。
clf.fit(x, y)
(4)调用svm中的score()方法,考查其训练效果。
rv=clf.score(x, y); # 模型准确率(针对训练数据)
(5)调用svm中的predict()方法,对测试样本进行预测,获得其预测结果。
R=clf.predict(x1)
示例代码如下:
import pandas as pd
data = pd.read_excel('car.xlsx')
x = data.iloc[:1690,:6].as_matrix()
y = data.iloc[:1690,6].as_matrix()
x1= data.iloc[1691:,:6].as_matrix()
y1= data.iloc[1691:,6].as_matrix()
from sklearn import svm
clf = svm.SVC(kernel='rbf')
clf.fit(x, y)
rv=clf.score(x, y);
R=clf.predict(x1)
Z=R-y1
Rs=len(Z[Z==0])/len(Z)
print('预测结果为:',R)
print('预测准确率为:',Rs)

相关文章:

【机器学习与实现】支持向量机SVM
目录 一、SVM (Support Vector Machine) 概述(一)支持向量机SVM的主要特点(二)支持向量与间隔最大化(三)线性可分/不可分(四)软间隔 (soft margin) 与核技巧 (kernel trick)…...

当代人工智能三教父——深度学习三巨头
文章目录 引言 人物介绍 突出贡献 专业名词解释 引言 今天下午闲来无事翻阅了一下csdn首页的头条文章——《27 岁天才创始人 Joel Hellermark 分享了自己和“AI 教父” Geoffery Hinton 的最新采访》 感觉挺有意思,就从头到尾的看了一遍,里面有很多…...

Django项目从创建到开发以及数据库连接的主要步骤,精简实用
1、项目创建 安装命令:pip install django3 -i <https://pypi.tuna.tsinghua.edu.cn/simple>上述命令是使用清华镜像,安装django3在项目的创建目录执行命令:django-admin startproject 项目名称(英文)就可以在指…...

linux 命令 grep 排除 No such file or directory
du -sh * 2>&1 | grep -v "proc" command 2>&1 | grep -v "No such file or directory" 这里的 2>&1 是将错误输出重定向到标准输出,然后 grep -v "No such file or directory" 会过滤掉包含 &qu…...
Unity 滑动条(Slider)拖拽开始和结束、点击等事件的拓展功能
目录 前言 一、关于slider的监听事件 二、方案一 (无脚本版) 三、方案二 (继承slider脚本进行拓展) 四、方案三(外部脚本添加) 前言 前一段时间在使用这个功能,发现搜索出来的文章和脚本&…...
持续更新 Linux输出重定向 Linux通配符 Linux正则表达式 持续更新....)
Linux 学习知识 (简单易懂 )持续更新 Linux输出重定向 Linux通配符 Linux正则表达式 持续更新....
一.输出重定向 标准输出:是将信息输出在终端 标准错误输出:在执行命令的过程中所产生错误信息也是输出在终端标准输入:从键盘输入 1.1标准输出重定向 作用:将本来要显示在终端上的信息重定向到一个文件中 实现方法:…...
前端vue用el-table如何实现表头内容过长换行处理,实现换行效果
前端vue用el-table如何实现表头内容过长换行处理,实现换行效果 这是效果图 有两种方法,一种简易版本,一种万能方法,都是el-table,先看文档 表头标题是可以自定义的 方法一 label的解释写在代码里面了,这里会自动形成换…...

15:00面试,15:08出来,面试问的有点变态。。。。
🍅 视频学习:文末有免费的配套视频可观看 🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天…...

【BUG】流式响应requests得到: ping - 和时间戳
前情提要 运行Langchain-Chatchat项目,使用自定义请求访问API Server流式输出 报错展示 b: ping - 2024-05-22 00:46:04.83252000:00\r\n\r\n报错原因 这通常是由于 Server-Sent Events (SSE) 实现中使用的“心跳”机制,以确保连接保持活跃。一些 SSE…...

人工智能应用-实验5-BP 神经网络分类手写数据集
文章目录 🧡🧡实验内容🧡🧡🧡🧡代码🧡🧡🧡🧡分析结果🧡🧡🧡🧡实验总结🧡🧡 ǹ…...

K8s Pod 资源进阶
文章目录 K8s Pod 资源进阶pod 资源限制限制资源单位 资源限制实战Pod 服务质量QosDownward API可注入的元数据信息环境变量方式注入元数据存储卷方式注入元数据为注册服务注入Pod 名称为 JVM 注入堆内存限制 K8s Pod 资源进阶 pod 资源限制 资源限制的方法: Req…...

掌握Edge浏览器的使用技巧
导言: Edge浏览器是微软推出的一款现代化、高效的网络浏览器。它不仅提供了基本的浏览功能,还具备了许多强大的特性和技巧,可以帮助用户更好地利用浏览器进行工作和娱乐。本文将介绍一些Edge浏览器的使用技巧,帮助读者更好地掌握这…...
Qt封装ping命令并将ping结果显示到界面
实现界面及在Windows 10下的运行结果如下: 代码如下: pingNetWork.h // 检测网络是否ping通的工具#ifndef PINGNETWORK_H #define PINGNETWORK_H#include <QWidget> #include"control_global.h" namespace Ui { class CPingNetWork; }c…...
图论(洛谷刷题)
目录 前言: 题单: P3386 【模板】二分图最大匹配 P1525 [NOIP2010 提高组] 关押罪犯 P3385 【模板】负环 P3371 【模板】单源最短路径(弱化版) SPFA写法 Dij写法: P3385 【模板】负环 P5960 【模板】差分约束…...
安卓部署ffmpeg全平台so并实现命令行调用
安卓 FFmpeg系列 第一章 Ubuntu生成ffmpeg安卓全平台so 第二章 Windows生成ffmpeg安卓全平台so 第三章 生成支持x264的ffmpeg安卓全平台so 第四章 部署ffmpeg安卓全平台so并使用(本章) 文章目录 安卓 FFmpeg系列前言一、添加so1、拷贝ffmpeg到项目2、bu…...

Go语言中MD5盐值加密解决用户密码问题
1. 用户密码存储的挑战 在Web应用开发中,用户密码的安全存储是一个核心问题。明文存储用户密码是极其危险的,因为一旦数据库被泄露,攻击者就可以直接获取用户的密码。为了保护用户密码,我们需要采取加密措施。 2. MD5算法简介 …...

flutter开发实战-本地SQLite数据存储
flutter开发实战-本地SQLite数据库存储 正在编写一个需要持久化且查询大量本地设备数据的 app,可考虑采用数据库。相比于其他本地持久化方案来说,数据库能够提供更为迅速的插入、更新、查询功能。这里需要用到sqflite package 来使用 SQLite 数据库 预…...

【路由組件】
完成Vue Router 安装后,就可以使用路由了,路由的基本使用步骤,首先定义路由组件,以便使用Vue Router控制路由组件展示与 切换,接着定义路由链接和路由视图,以便告知路由组件渲染到哪个位置,然后…...

【C++风云录】数字逻辑设计优化:电子设计自动化与集成电路
集成电路设计:打开知识的大门 前言 本文将详细介绍关于数字芯片设计,电子设计格式解析,集成电路设计工具,硬件描述语言分析,电路验证以及电路优化六个主题的深入研究与实践。每一部分都包含了主题的概述,…...
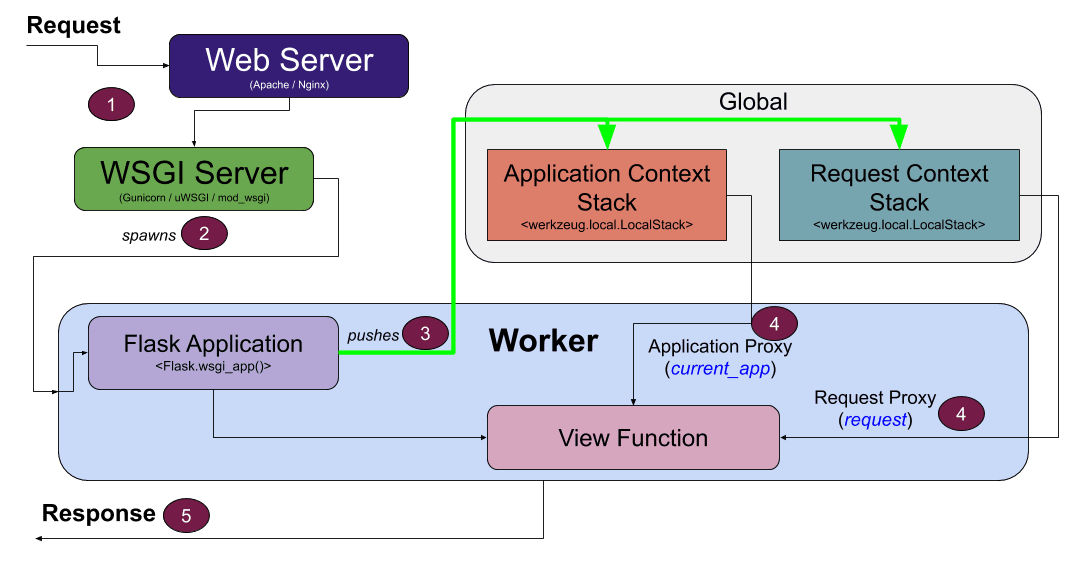
Flask Response 对象
文章目录 创建 Response 对象设置响应内容设置响应状态码设置响应头完整的示例拓展设置响应的 cookie重定向响应发送文件作为响应 总结 Flask 是一个 Python Web 框架,用于快速开发 Web 应用程序。在 Flask 中,我们使用 Response 对象来构建 HTTP 响应。…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...
