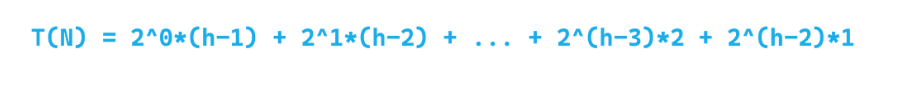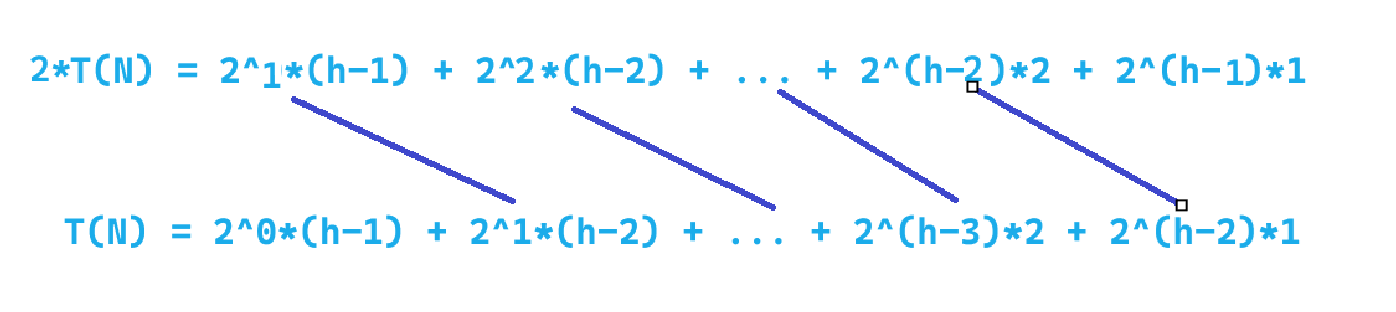[建堆堆排序的时间复杂度推导]向上建堆向下建堆堆排序的时间复杂度分析推导
💖💖💖欢迎来到我的博客,我是anmory💖💖💖
又和大家见面了
欢迎来到动画详解数据结构系列
作为一个程序员你不能不掌握的知识
先来自我推荐一波
个人网站欢迎访问以及捐款
推荐阅读
如何低成本搭建个人网站
专栏:动画详解leetcode算法题
C语言知识
前导知识:求二叉树的节点个数
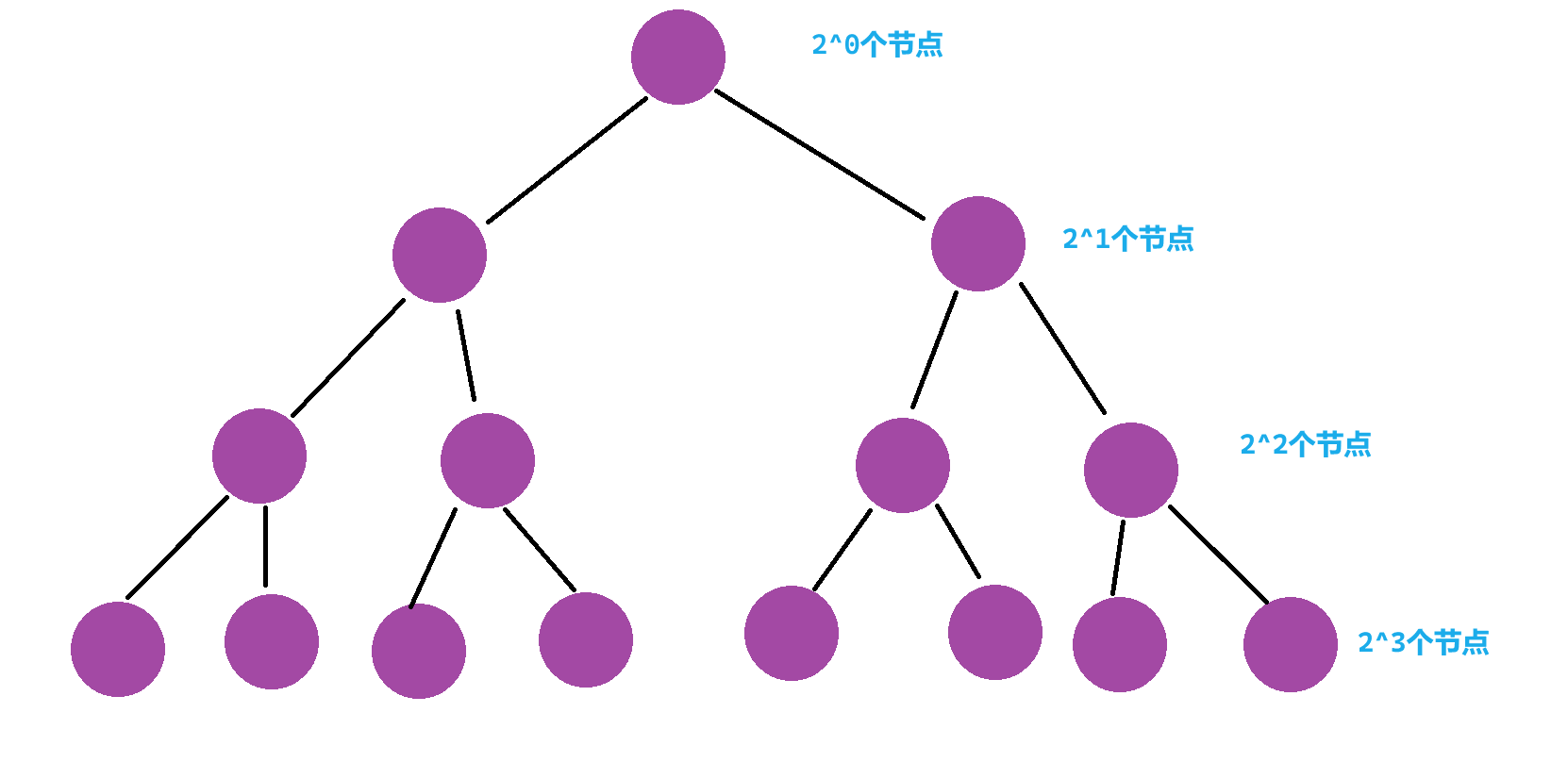
满二叉树的节点个数
对于一个满二叉树,每一层都满足等比数列,所以其节点个数总和我们可以使用等比数列求和公式来计算
我们假设满二叉树的高度是 h h h,节点个数是 N N N
因此,满二叉树的节点个数是 N = 2 h − 1 N = 2^h-1 N=2h−1
满二叉树的高度是 h = l o g 2 ( N + 1 ) h = log_2(N+1) h=log2(N+1)
最后一层只有一个节点的二叉树的节点个数
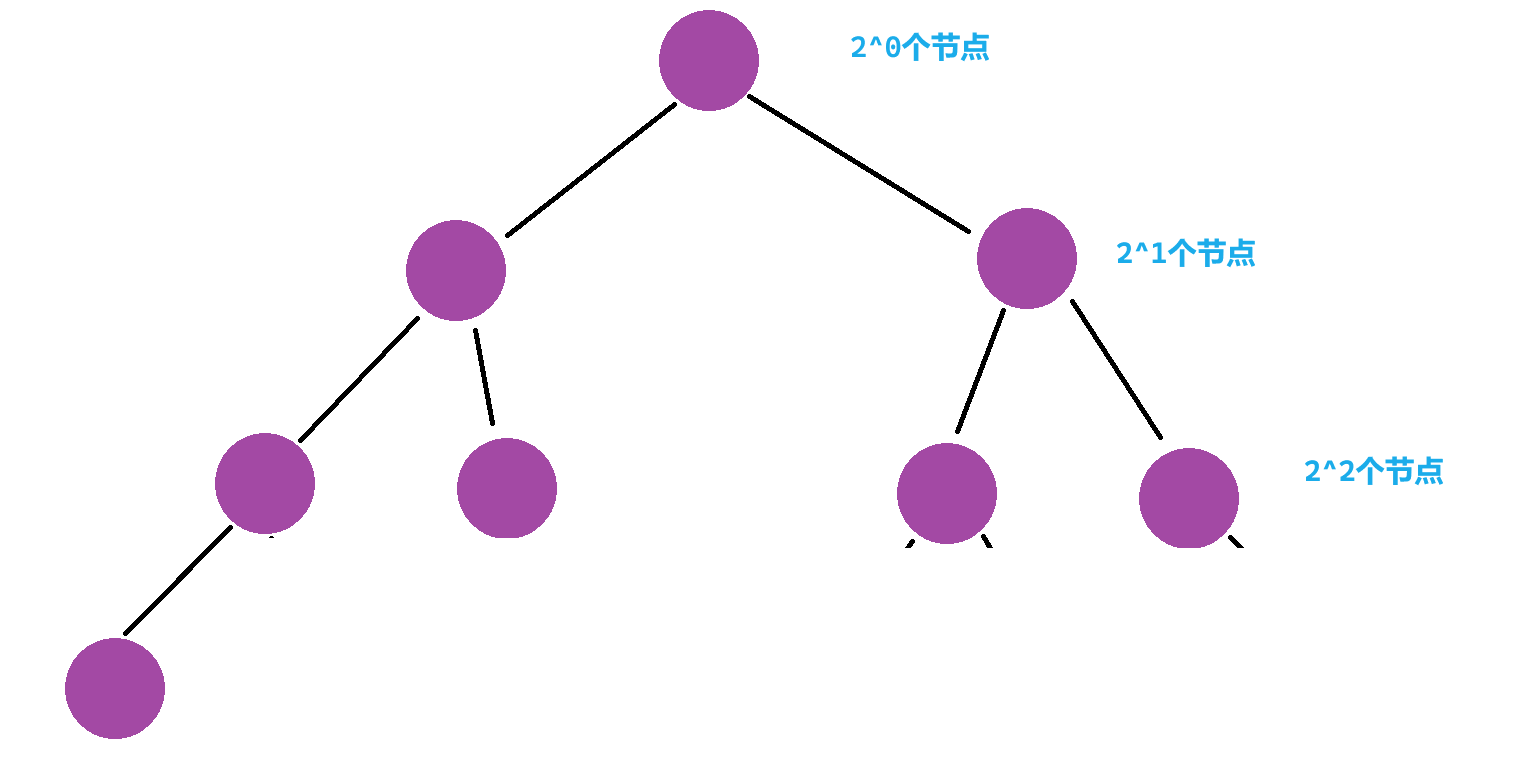
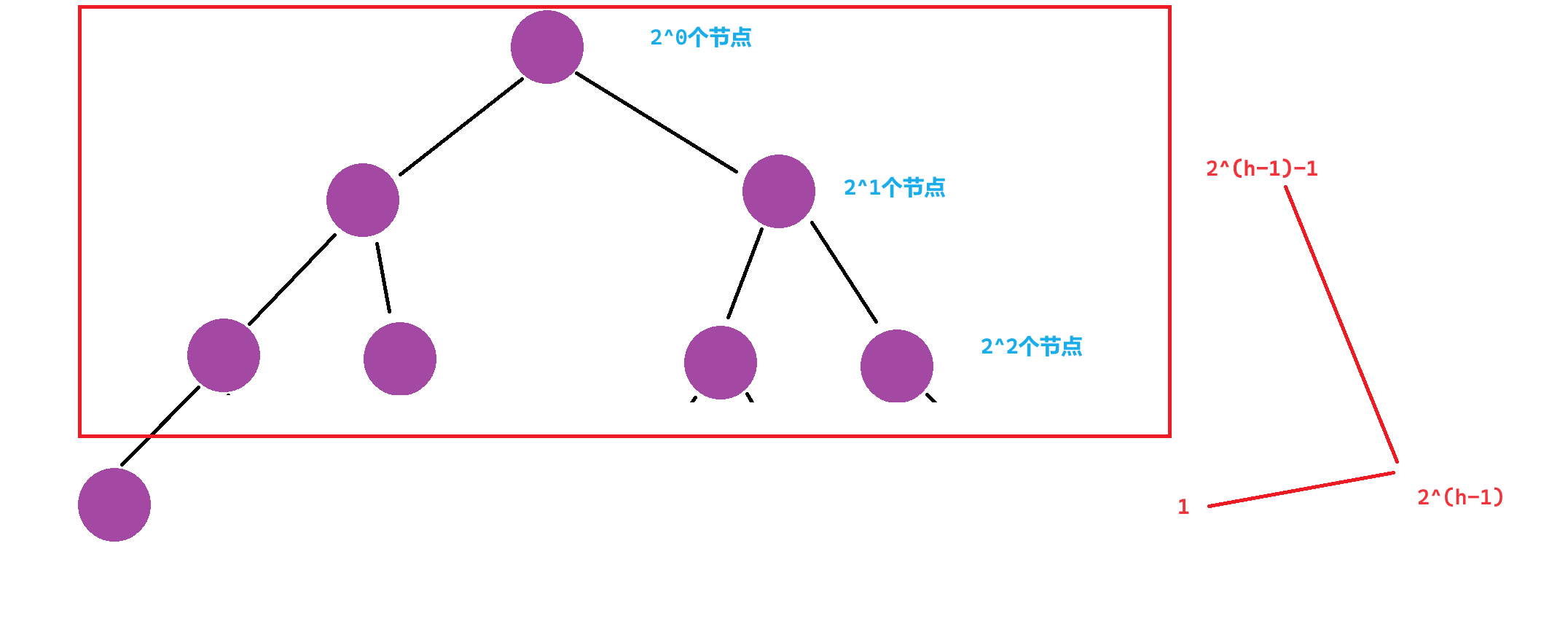
这样的二叉树的节点个数为 N N N= 2^h-1
高度为 h = l o g 2 N h=log_2N h=log2N
向下建堆的时间复杂度推导
向下建堆代码
// 向下调整函数
// n是指堆中有效元素的数量, parent是指堆顶的元素
// 需要比较子节点哪个大哪个小
void AdjustDown(HPDataType* a, int n,int parent)
{// 先假设左孩子大int child = parent * 2 + 1;while (child < n)// 当child>=n时就说明child已经到达叶子节点了{// 先找出左右孩子节点中大的那个if (child + 1 < n && a[child + 1] > a[child])// 说明假设错误,交换小的那个子节点{child++;}// 和父亲节点进行比较if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
向下建堆的时间复杂度推导
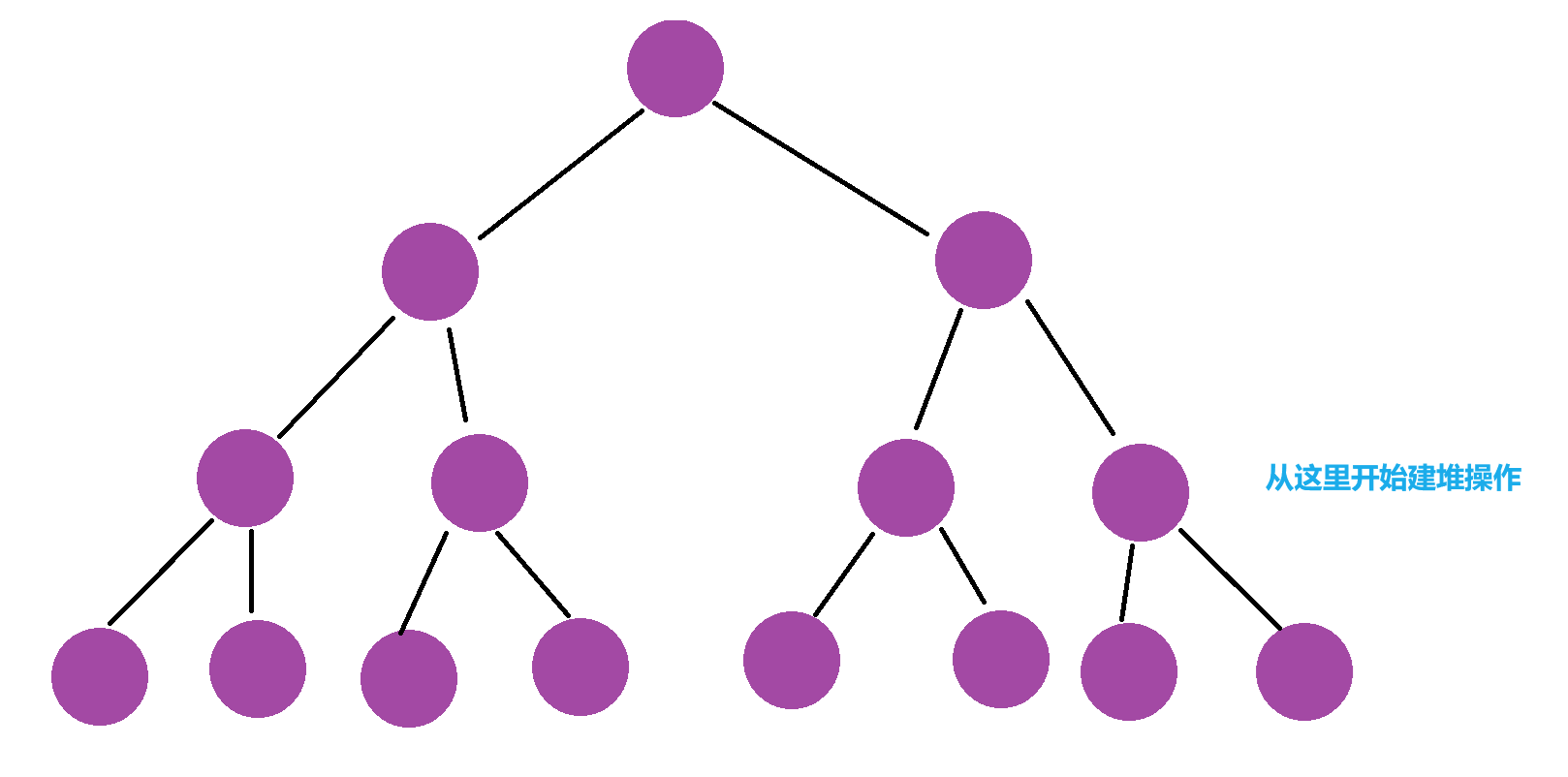
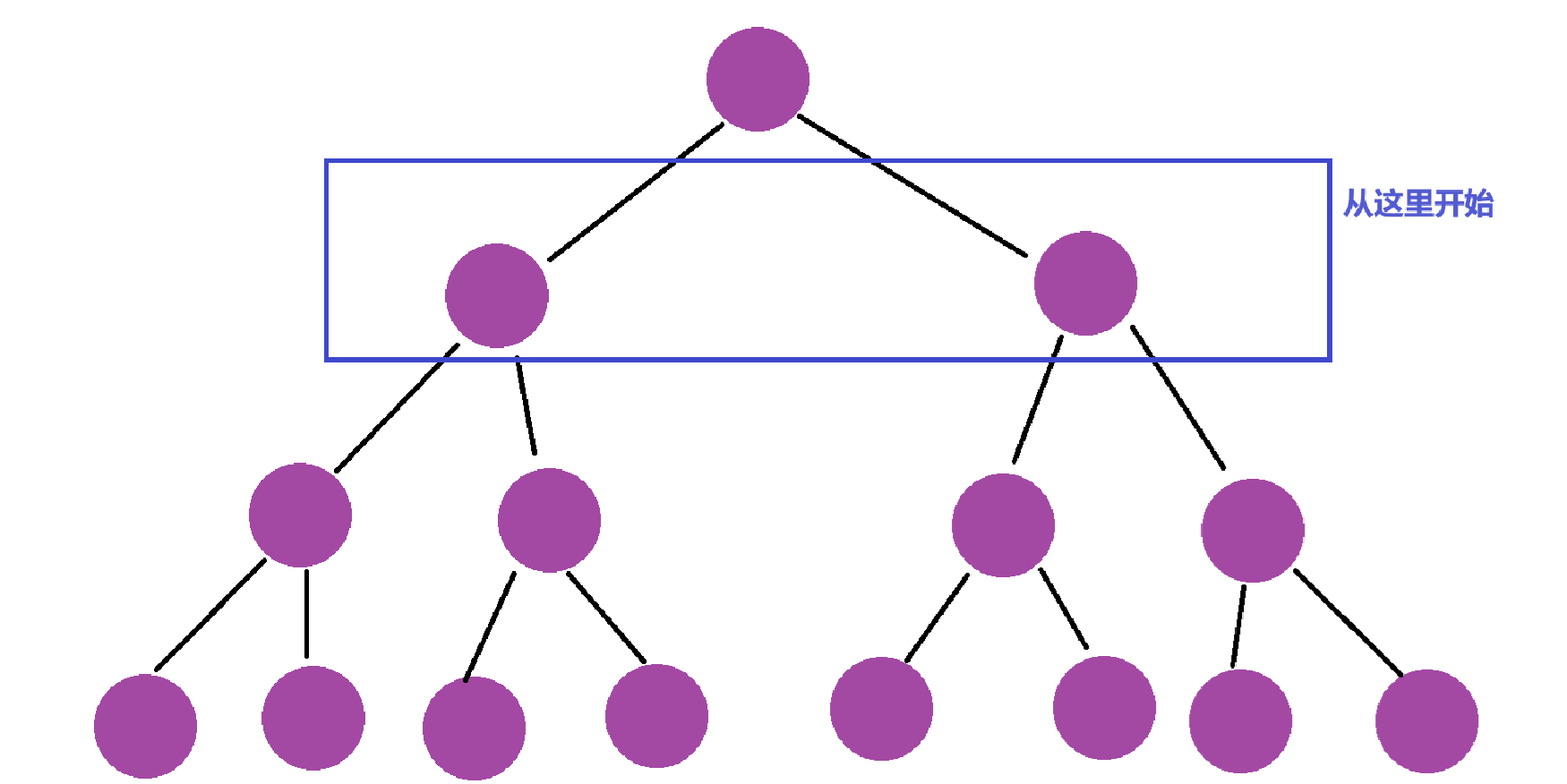
首先我们需要明白的是向下建堆是从倒数第一个非叶子节点开始建堆的
知道了这个之后,我们就可以开始考虑最坏的建堆情况,也就是每一次都要向下调整
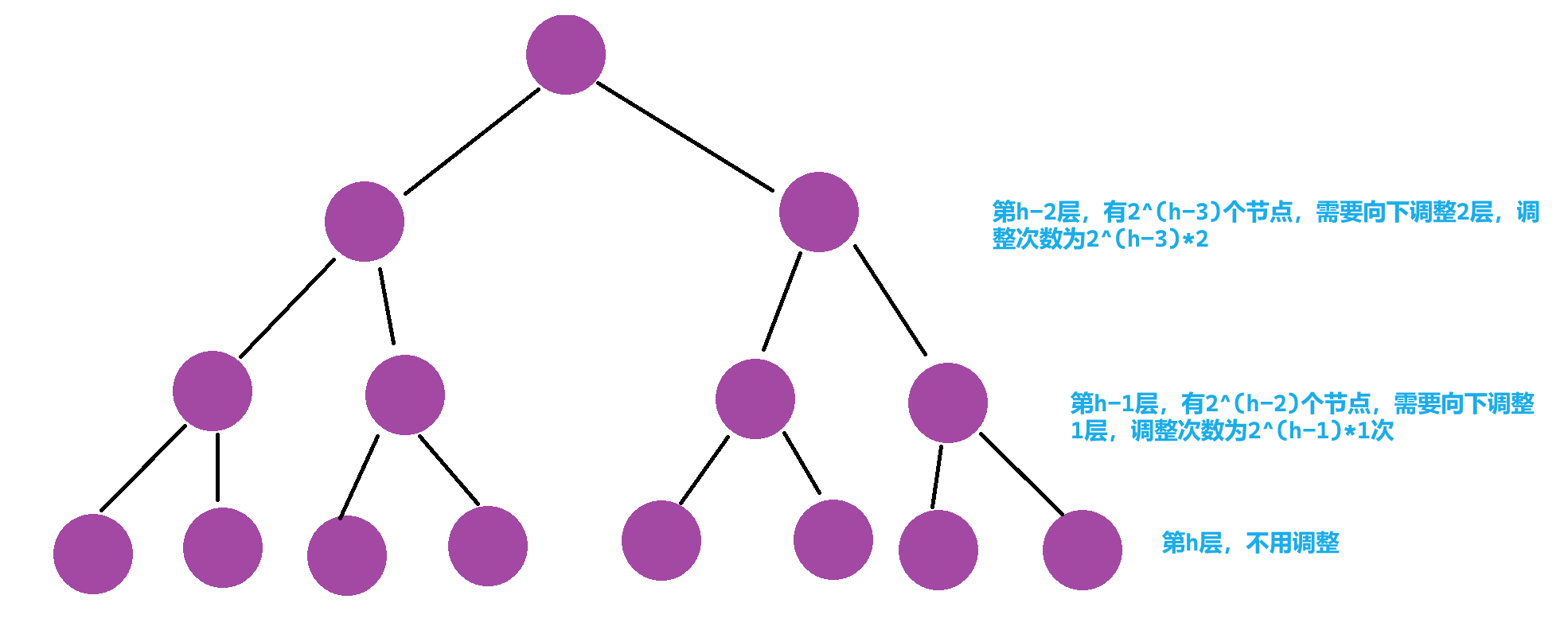
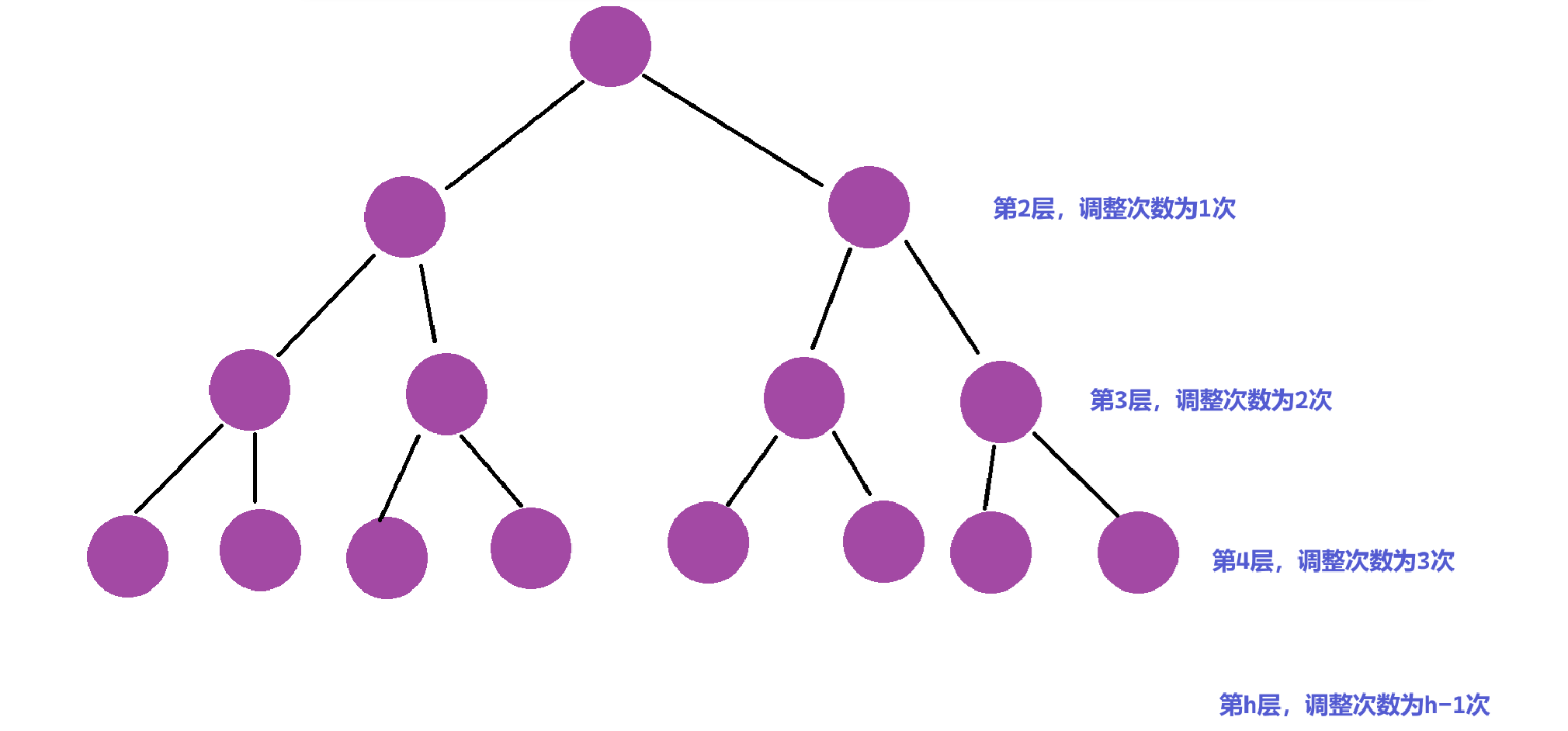
依旧假设高度为 h h h,我们可以算出每一层需要调整的次数
因此我们不难列出总的调整次数的公式
那么,要想算出 T ( N ) T(N) T(N),我们就可以使用错位相减法来对其进行求和
因此,向下调整的总次数为:
因此我们可以得到向下调整建堆的时间复杂度是
O ( N ) O(N) O(N)
除此之外,我们还可以发现
节点数多的调整的次数就少
节点数少的调整的次数就多
向上建堆的时间复杂度推导
向上建堆代码
// 向上调整函数
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child){// 大堆调整if (a[child] > a[parent]){Swap(&a[child], a[parent]);child = parent;parent = (child - 1) / 2;}// 若已经满足大堆,那么就跳出循环else{break;}}
}
向上建堆复杂度推导
向上调整建堆是从第二层开始的
因此我们可以算出调整的总次数
因此我们可以算出向上调整建堆的时间复杂度为
O ( N l o g N ) O(NlogN) O(NlogN)
除此之外我们可以发现
节点数少的层调整次数少
节点数多的层调整次数多
堆排序的时间复杂度推导
堆排序代码
// 对数组进行堆排序,需要建堆
void HeapSort(int* a, int n)
{// 降序,建小堆// 升序,建大堆for (int parent = (n-1-1)/2; parent > 0; parent--){AdjustDown(a, n, parent);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
堆排序的时间复杂度推导
我们可以发现,第一个for循环使用了向下调整建堆,其复杂度为 O ( N ) O(N) O(N)
第二个循环按理来说应该是 O ( N 2 ) O(N^2) O(N2)
但因为第二个循环并非是最坏的情况,所以我们认为其时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
因此,堆排序的时间复杂度就为
O ( N l o g N ) O(NlogN) O(NlogN)
💖💖💖非常感谢各位的支持💖💖💖
我们共同进步
本系列持续更新,关注我,带你了解更多数据结构知识
下期再见
相关文章:

[建堆堆排序的时间复杂度推导]向上建堆向下建堆堆排序的时间复杂度分析推导
💖💖💖欢迎来到我的博客,我是anmory💖💖💖 又和大家见面了 欢迎来到动画详解数据结构系列 作为一个程序员你不能不掌握的知识 先来自我推荐一波 个人网站欢迎访问以及捐款 推荐阅读 如何低成本搭…...

【C++初阶】--- C++入门(上)
目录 一、C的背景及简要介绍1.1 什么是C1.2 C发展史1.3 C的重要性 二、C关键字三、命名空间2.1 命名空间定义2.2 命名空间使用 四、C输入 & 输出 一、C的背景及简要介绍 1.1 什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题&…...

安装和使用图像处理软件GraphicsMagick @FreeBSD
GraphicsMagick是一个用于处理图像的读取、写入和操作的工具软件。它被誉为图像处理领域的“瑞士军刀”,短小精悍,支持超过88种图像格式,包括DPX、GIF、JPEG、JPEG-2000、PNG、PDF、PNM和TIFF等。 GraphicsMagick的主要特点包括:…...

一款功能强大的安卓虚拟机应用——VMOS Pro使用分享
前段时间我刚刚分享一个WeChat平板模块能够允许用户自由修改系统设置,让你的Android备用手机焕发新生,实现手机PAD化,实现两台设备同时登录微信号。今天我分享的这个相比WeChat更为简单,因为它可以通过虚拟机的方式进行多种androi…...
【408真题】2009-12
“接”是针对题目进行必要的分析,比较简略; “化”是对题目中所涉及到的知识点进行详细解释; “发”是对此题型的解题套路总结,并结合历年真题或者典型例题进行运用。 涉及到的知识全部来源于王道各科教材(2025版&…...
)
vue3第三十三节(TS 之 computed watch)
vue3 组合是API 中我们经常使用的 监听函数 computed 和 watch使用 1、computed 里面添加类型 <script setup lang"ts"> import { ref, computed } from vue const age ref(18) // 定义一个Person 接口 interface Person {age: numbername: string } const…...

工厂模式(简单工厂模式+工厂模式)
工厂模式的目的就是将对象的创建过程隐藏起来,从而达到很高的灵活性,工厂模式分为三类: 简单工厂模式工厂方法模式抽象工厂模式 在没有工厂模式的时候就是,客户需要一辆马车,需要客户亲自去创建一辆马车,…...
)
整理好了!2024年最常见 20 道 Redis面试题(四)
上一篇地址:整理好了!2024年最常见 20 道 Redis面试题(三)-CSDN博客 七、Redis 单线程模型是如何工作的? Redis 是一个基于单线程模型的高性能键值存储数据库。尽管 Redis 操作大多数是单线程执行的,但它…...
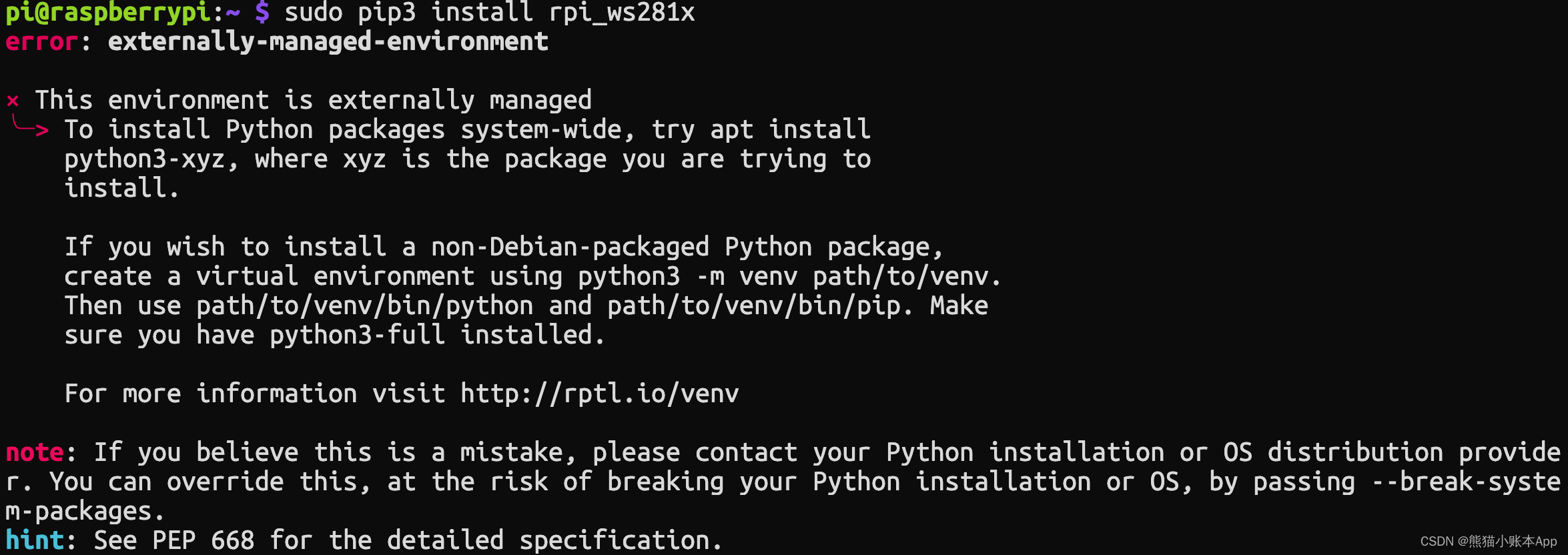
sudo pip3 install rpi_ws281x error: externally-managed-environment
报错 error: externally-managed-environment piraspberrypi:~ $ sudo pip3 install rpi_ws281x error: externally-managed-environment This environment is externally managed ╰─> To install Python packages system-wide, try apt installpython3-xyz, where xyz i…...
day08-Java常用API
day08——Java常用API 一、今日内容介绍、API概述 各位同学,我们前面已经学习了面向对象编程,使用面向编程这个套路,我们需要自己写类,然后创建对象来解决问题。但是在以后的实际开发中,更多的时候,我们是…...

设计模式--建造者模式
建造者模式是一种创建型设计模式,它允许用户通过一步一步地构建对象来创建复杂的对象。这种模式在许多应用场景中非常有用,例如在创建具有多个可选参数的对象、构建具有多种配置的对象以及生成具有多个部分的对象时。 应用场景 创建具有多个可选参数的…...

运行时间比较
subprocess.run() 函数参数的含义: shell_command:这是要执行的命令。它可以是一个字符串,也可以是一个包含命令和参数的列表。例如,“ls -l” 或 [“ls”, “-l”]。shellTrue:这是一个布尔值参数,指示是…...
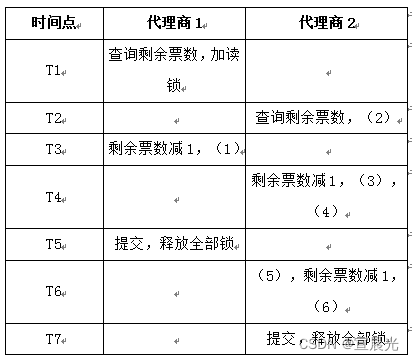
【系统架构师】-案例篇(十四)数据库与分布式
1、规范化 不满足3NF,导致的存储异常 原关系模式 航班(航班编号,航空公司,起飞地,起飞时间,目的地,到达时间,剩余票数,票价) 代理商(代理商编号…...
Golang实现递归复制文件夹
代码 package zdpgo_fileimport ("errors""os""path/filepath""strings" )// CopyDir 复制文件夹 // param srcPath 源文件夹 // param desPath 目标文件夹 // return error 错误信息 func CopyDir(srcPath, desPath string) error {…...

【漏洞复现】用友U8 CRM uploadfile 文件上传致RCE漏洞
0x01 产品简介 用友U8 Cloud是用友推出的新一代云ERP,主要聚焦成长型、创新型企业,提供企业级云ERP整体解决方案。 0x02 漏洞概述 用友 U8 CRM客户关系管理系统 uploadfle.php 文件存在任意文件上传漏洞,未经身份验证的攻击者通过漏洞上传…...

键盘盲打是练出来的
键盘盲打是练出来的,那该如何练习呢?很简单,看着屏幕提示跟着练。屏幕上哪里有提示呢?请看我的截屏: 截屏下方有8个带字母的方块按钮,这个就是提示,也就是我们常说的8个基准键位,我…...

构建sqli-labs学习环境与掌握SQL注入技术教程
根据提供的文档内容,以下是关于安装sqli-labs学习环境和SQLI-LABS教学的详细步骤和知识点: 安装sqli-labs学习环境 环境准备 操作系统:CentOS 7.6主机名:xuegod63IP地址:192.168.1.63 关闭防火墙和SELinux 禁用并…...

力扣HOT100 - 1143. 最长公共子序列
解题思路: 动态规划 class Solution {public int longestCommonSubsequence(String text1, String text2) {int m text1.length(), n text2.length();int[][] dp new int[m 1][n 1];for (int i 1; i < m; i) {char c1 text1.charAt(i - 1);for (int j 1…...

【贪心算法题目】
1. 柠檬水找零 这一个题目是一个比较简单的模拟算法,只需要根据手里的钱进行找零即可,对于贪心的这一点,主要是在20元钱找零的情况下,此时会出现两种情况:10 5 的组合 和 5 5 5 的组合,根据找零的特点&a…...

yarn常用命令
Yarn 是一个快速、可靠且安全的依赖管理工具,用于替代 npm。以下是一些常用的 Yarn 命令,用于不同的包管理和项目依赖安装场景: 初始化一个新的项目 yarn init这个命令会引导你创建一个 package.json 文件。 安装依赖 yarn add [package]…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...