R实验 参数检验(二)
- 实验目的:
- 掌握正态分布和二项分布中,功效与样本容量之间的关系;
- 学会利用R软件完成一个正态总体方差和两个正态总体方差比的区间估计和检验。
实验内容:
(习题5.28)一种药物可治疗眼内高压,目的是阻止青光眼的发展。现试验了 10 名病人,治疗一个月后,他们的眼压平均降低了 5mmHg ,且标准差为 10mmHg。其功效为多少?如果功效在80% 以上,应当至少选择多少名试验者?
提示:此题是单个正态总体的功效和样本容量的计算问题。参考例5.34。在使用power.t.test()函数时,参数delta=5,sd=10。
解:
(1)功效是多少?
功效大约为0.184
源代码及运行结果:(复制到此处,不要截图)
> power.t.test(10,delta = 5,sd = 10)Two-sample t test power calculation
n = 10
delta = 5
sd = 10
sig.level = 0.05
power = 0.1838375
alternative = two.sided
NOTE: n is number in *each* group
结论:此时功效为0.184,功效偏低
(2)功效在80% 以上,应当至少选择多少名试验者?
功效在80%以上,至少要选择64名实验者
源代码及运行结果:(复制到此处,不要截图)
> power.t.test(power = 0.80,delta = 5,sd = 10)Two-sample t test power calculation
n = 63.76576
delta = 5
sd = 10
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
结论:n=63.77.至少取64名实验者
(习题5.29)为了检测某种药物服用后可能导致血压升高,找了8名药物服用者,他们的平均收缩压为 132.86 mmHg ,样本标准差为 15.34 mmHg。对照组共 21 人,他们的平均收缩压为127.44 mmHg ,样本标准差为 18.23 mmHg。 如果假设数据服从正态分布,试分析该药物服用后是否能导致血压升高?检验的功效是多少?如果功效要达到 80 每组至少取多少个样本?
t test power calculation n1 = 31.2884 n2 = 21 d = 0.8058214 sig.level = 0.05 power = 0.8 alternative = two.sided |
提示:此题是两个正态总体的功效和样本容量的计算问题。参考例5.35。但此题与例5.35略有不同:此题的两个样本标准差不相同,因此在使用power.t.test()函数时,参数sd需要按P127公式(5.46)中的分母来计算。另外,也可以使用pwr包来计算功效。
解:
(1)功效是多少?
功效大约为0.464
源代码及运行结果:(复制到此处,不要截图)
> library(pwr)> n1<-8> n2<-21> mean_diff<- 132.86-127.44> sd1<-15.34> sd2<-18.23> pwr.t2n.test(n1 = n1,n2 = n2,d = mean_diff/sqrt((sd1^2/n1)+(sd2^2/n2)))t test power calculation
n1 = 8
n2 = 21
d = 0.8058214
sig.level = 0.05
power = 0.4643853
alternative = two.sided
结论:此时功效为0.464,功效偏低
(2)功效在80% 以上,应当至少选择多少名试验者?
功效在80%以上,至少要选择32名实验者
源代码及运行结果:(复制到此处,不要截图)
结论:n=31.3,至少要选择32名实验者
(习题5.30)对于习题 5.26 ,如果要求功效达到 80% 以上,试验时至少选择多少个样本?
提示:此题是两个总体比例的功效和样本容量的计算问题。参考例5.36。
解:
源代码及运行结果:(复制到此处,不要截图)
power.prop.test(power = 0.8,p1 = 34/70, p2 = 31/80)Two-sample comparison of proportions power calculation
n = 399.1236
p1 = 0.4857143
p2 = 0.3875
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group
结论:n=399.12,至少要选择400个样本,才能让功效达到80%
(习题5.31)某汽车公司要求员工恪守时间,以在公众面前树立良好的值得信赖的形象。公司要求各个汽车的汽车到站时间的变化不能太大,具体要求是:到站时间的标准差不能超过2分钟。公司在某市的汽车中转站随机地抽取了 10 次汽车的到站时间如下(单位:分钟):
15 .2 17.5 19.6 16.6 21 . 3 17.1 15.0 15.5 20.0 16.2
试分析该公司的汽车司机是否遵守时间规定?
> source("C:\\Users\\黄培滇\\Desktop\\R语言生物统计学\\chap05\\var1.test.R")> X<-c(15.2,17.5,19.6,16.6,21.3,17.1,15.0,15.5,20.0,16.2)> var1.test(X,var = 2^2,alternative = "less")| $X.squared [1] 10.8 $sample.var [1] 4.8 $df [1] 9 $conf.inter [1] 0.00000 12.99204 $p.value [1] 0.7103325 |
提示:此题是单个正态总体的方差检验。参考例5.37。
解:提出假设:
H0:σ2≥22
H1:σ2<22
源代码及运行结果:(复制到此处,不要截图)
结论:P值>0.05,接受原假设,即到站时间的标准差超过2分钟
(习题5.32)对习题5.16中甲乙两种稻种的数据作方差比的区间估计,并用其估计值来判定两数据是否等方差。若两数据方差不相等,试重新计算两稻种产量的期望差m1-m2的置信区间(a =0.05)。
提示:在R软件中,var.test()函数能够提供两个样本方差比的区间估计。此结果可认为方差不等。因此重新计算期望差时应该采取方差不等的参数。
解:
源代码及运行结果:(复制到此处,不要截图)
> a<-c(140,137,136,140,145,148,140,135,144,141)> b<-c(135,118,115,140,128,131,130,115,131,125)> Table<-data.frame(a,b)> var.test(a,b)F test to compare two variances
data: a and b
F = 0.23533, num df = 9, denom df = 9, p-value =
0.04229
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.05845276 0.94743902
sample estimates:
ratio of variances
0.2353305
> t.test(a,b,var.equal = F)Welch Two Sample t-test
data: a and b
t = 4.6287, df = 13.014, p-value = 0.0004712
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
7.359713 20.240287
sample estimates:
mean of x mean of y
结论:var.test()计算结果中,P值<0.05,且置信区间不包含1,这说明两者方差并不相等,且重新求出其95%置信区间为7.40,,20.24
(习题5.33)检验习题5.24中试验组和对照组的数据的方差是否相同。
提示:此题是两个正态总体的方差检验。参考例5.38。
解:提出假设:
H0:σ12=σ22
H1:σ12≠σ22
源代码及运行结果:(复制到此处,不要截图)
> 甲<-c(140,137,136,140,145,148,140,135,144,141)> 乙<-c(135,118,115,140,128,131,130,115,131,125)> Table<-data.frame(甲,乙)> with(Table,var.test(甲,乙))F test to compare two variances
data: 甲 and 乙
F = 0.23533, num df = 9, denom df = 9, p-value =
0.04229
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.05845276 0.94743902
sample estimates:
ratio of variances
0.2353305
结论:P值<0.05,拒绝原假设,即试验组和对照组的数据的方差存在差异
思考:
检验功效 p 就是正确地否定了错误的原假设的概率,即 p = 1-β,其中 β 称为犯第 二 类错误的概率。在R软件,利用 power.t.test() 函数可以完成正态分布均值(差)的检验功效或样本容量的计算;利用 pwr.prop.test() 函数可以完成两组数据比率差的检验功效或样本容量的计算。
影响均值检验功效的因素有:
样本量n:其他条件不变情况下,样本量越大,发生第二类错误的概率 β (包括第一类错误的概率)越小,因此功效越__高___;
差异Δ(两总体时是μ1-μ2,单总体时是μ1-μ0):以单个总体为例,其他条件不变情况下,差异越大,说明样本与总体之间的差异越大,越容易被检验出来,因此统计功效越__高__。
样本标准差σ:σ越小,功效越大。
显著性水平α:由于α与 β 是此消彼涨的关系,因此α越大,β 越小,因此功效越__高___;
事实上,上述前3个因素①②③与功效共4个量,知道其中3个,就可以求出另一个。这也是power.t.test()函数中最重要的几个参数。
单个正态总体的方差的区间估计和检验(设样本容量为n)
当这个总体的均值μ已知时,用到的是哪个分布?
正态分布
当这个总体的均值μ未知时,用到的是哪个分布?
t分布
两个正态总体的方差比的区间估计和检验(设两个样本容量分别为n1、n2)
当这两个总体的均值μ1、μ2已知时,用到的是哪个分布?
F分布
当这两个总体的均值μ1、μ2未知时,用到的是哪个分布?
F分布
在R的基本函数中,没有计算单个总体方差的区间估计与假设检验的函数;两个正态总体的情况下,可通过方差比的估计和检验来两个总体的方差是否相同,可以利用R软件中的 var.test() 函数来完成。
相关文章:
)
R实验 参数检验(二)
实验目的:掌握正态分布和二项分布中,功效与样本容量之间的关系;学会利用R软件完成一个正态总体方差和两个正态总体方差比的区间估计和检验。 实验内容: (习题5.28)一种药物可治疗眼内高压,目的…...

【Linux】进程信号及相关函数/系统调用的简单认识与使用
文章目录 前言一、相关函数/系统调用1. signal2. kill3. abort (库函数)4. raise (库函数)5. alarm 前言 现实生活中, 存在着诸多信号, 比如红绿灯, 上下课铃声…我们在接收到信号时, 就会做出相应的动作. 对于进程也是如此的, 进程也会收到来自 OS 发出的信号, 根据信号的不同…...
什么是Spring Boot)
Spring (14)什么是Spring Boot
Spring Boot是一个开源的Java基础框架,旨在简化Spring应用的创建和开发过程。Spring Boot通过提供一套默认配置(convention over configuration),自动配置和启动器(starters)来减少开发者的开发工作量和配置…...

区间预测 | Matlab实现CNN-KDE卷积神经网络结合核密度估计多置信区间多变量回归区间预测
区间预测 | Matlab实现CNN-KDE卷积神经网络结合核密度估计多置信区间多变量回归区间预测 目录 区间预测 | Matlab实现CNN-KDE卷积神经网络结合核密度估计多置信区间多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现CNN-KDE卷积神经网络结合…...

Java集合框架全景解读:从源码到实践精通指南
1. Java集合框架简介 在Java中,集合框架是用于存储和处理数据集合的一组类和接口。它提供了一系列的数据结构,比如列表(List)、集(Set)和映射(Map)。这些数据结构为开发者处理数据提…...

Python | Leetcode Python题解之第107题二叉树的层序遍历II
题目: 题解: class Solution:def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:levelOrder list()if not root:return levelOrderq collections.deque([root])while q:level list()size len(q)for _ in range(size):node q.popl…...
H4vdo 台湾APT-27视频投放工具
地址:https://github.com/MartinxMax/H4vdo 视频 关于 H4vdo RTMP lock 屏播放视频工具,可以向目标发送有效载荷,播放目标的屏幕内容。目标无法曹作计算机 使用方法 安装依赖 根据你的操作系统选择一个安装程序 RTMP 服务端 ./rtsp-simple-server.…...

数据结构(树)
1.树的概念和结构 树,顾名思义,它看起来像一棵树,是由n个结点组成的非线性的数据结构。 下面就是一颗树: 树的一些基本概念: 结点的度:一个结点含有的子树的个数称为该结点的度; 如上图&#…...

HTML静态网页成品作业(HTML+CSS)——川西旅游介绍网页(2个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有2个页面。 二、作品演示 三、代…...
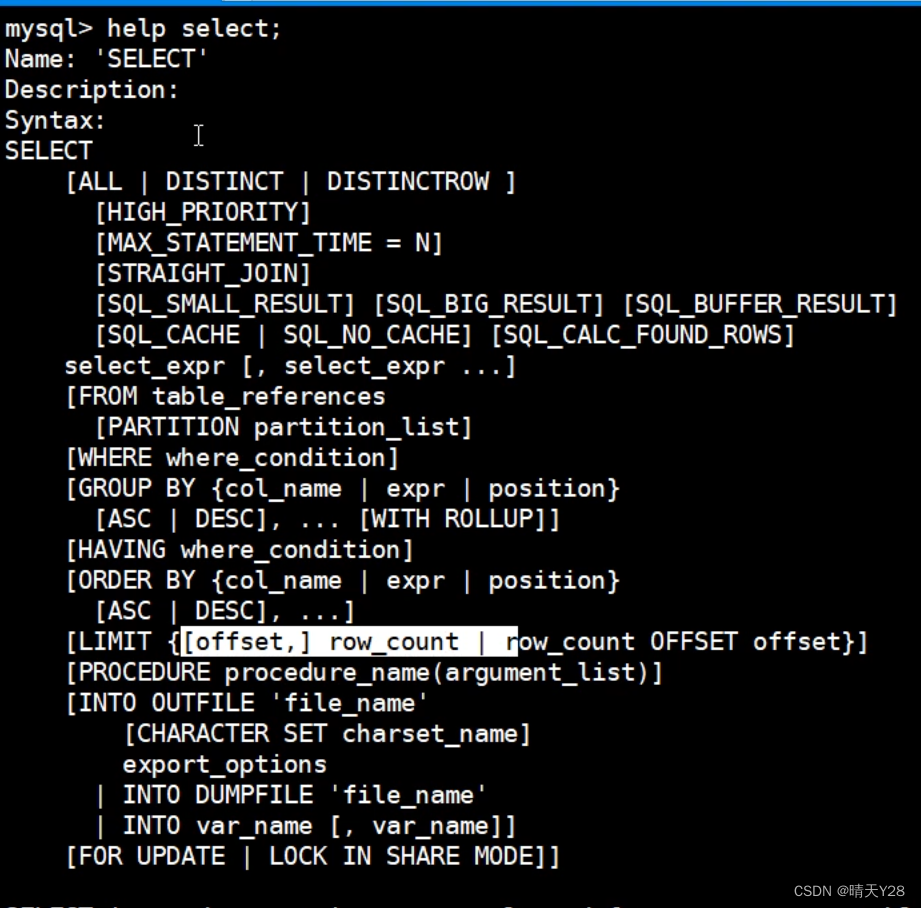
MySQL数据库单表查询中查询条件的写法
1.使用比较运算符作为查询条件 ; !; >; >; <; <; 如上图所示,可以使用命令select 字段,字段 from 表名 where Gender “M”; 即挑选出Gender “M” 的教师, 如上图所示,可以使用命令select 字段,…...

SQL靶场搭建
概述 简单介绍一下SQL靶场的搭建,以及在搭建过程中遇到的一些问题。使用该软件搭建靶场相对简单,适合新手小白。当然,也可以在自己的虚拟机下进行搭建,相对来说就较为复杂。本章主要讲解使用Phpstudy进行SQL靶场搭建。 这里我推…...

Cocos Creator 帧动画播放组件制作详解
前言 Cocos Creator 是一个强大的游戏开发工具,提供了丰富的功能和组件,其中帧动画播放组件是游戏开发中常用的组件之一,通过帧动画播放组件可以实现角色动画、特效动画等效果。本文将详细介绍如何使用 Cocos Creator 制作帧动画播放组件&am…...

基于STM32控制的双轮自平衡小车的设计
基于STM32控制的双轮自平衡小车的设计是一项涉及电子、控制理论、机械设计和编程的综合工程。以下是关于该设计的一个概述,包括关键组件、控制策略和示例代码。 设计概述 1. 项目背景 自平衡小车作为一种智能控制系统,其设计和实现涉及到多个学科领域…...

Dijkstra算法在《庆余年》中的应用:范闲的皇宫之旅
❤️❤️❤️ 欢迎来到我的博客。希望您能在这里找到既有价值又有趣的内容,和我一起探索、学习和成长。欢迎评论区畅所欲言、享受知识的乐趣! 推荐:数据分析螺丝钉的首页 格物致知 终身学习 期待您的关注 导航: LeetCode解锁100…...

HTML静态网页成品作业(HTML+CSS)——利物浦足球俱乐部介绍网页设计制作(5个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,共有5个页面。 二、作品演示 三、代码目录 四、网站代码 HTML部分代…...

mac 查看占用80端口的命令
在 Mac 上,如果你想查看哪个进程正在使用 80 端口,你可以使用 lsof 命令。这个命令非常强大,用于列出被进程打开或使用的文件信息。 打开你的终端,并输入以下命令: sudo lsof -i :80这里,-i :80 选项告诉…...
【Qt常用控件】—— 布局管理器
目录 前言 (一)垂直布局 (二)水平布局 (三)网格布局 (四)表单布局 (五)分组布局 (六)Spacer 总结 前言 之前使⽤Qt在界⾯上…...

模板中的右值引用(万能引用)、引用折叠与完美转发
模板中的右值引用(万能引用)、引用折叠与完美转发 文章目录 模板中的右值引用(万能引用)、引用折叠与完美转发一、万能引用与引用折叠1. 模板中的右值引用2. 自动类型推导(auto)与万能引用3. 引用折叠与万能引用4. lambda表达式捕…...

Nacos启动报错:[db-load-error]load jdbc.properties error
在学习Nacos中间件时,出现了一个错误,竟然启动报错!!!! 这个错误第一次遇见,当时我感觉大体就是--数据库连接方面的错误。 可是,对于初学者的我来说一脸懵啊??ÿ…...

5.23相关性分析
相关性分析是一件很自然而然的事情,在生活中和科学研究中,我们都可能会不由自主地关注两件或者多件事情之间的联系。比如性别和方向感有没有关系,有多大关系,辨别不同事物时如何说明特征的科学性(也就是该特征和事物的…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
