Python高克勒-曼宁-斯特里克勒公式计算一维流量
📜曼宁公式-用例
📜Python流体数据统计模型和浅水渗流平流模型模拟 | 📜Python蒸发散物理问题(微积分-线性代数-拉普拉斯和傅立叶变换)
✒️Python计算一维流量
高克勒-曼宁-斯特里克勒公式公式基于一维(横截面平均)流动特性的假设,将明渠水流的水深和流速联系起来。斯特里克勒公式是对纳维-斯托克斯方程和连续性方程进行大幅简化的结果。 尽管一维方法在很大程度上已被至少二维数值模型所取代,但一维斯特里克勒公式公式仍经常用作边界条件的第一近似值。
斯特里克勒公式的基本形式为:
u = k s t ⋅ S 1 / 2 ⋅ R h 2 / 3 u=k_{s t} \cdot S^{1 / 2} \cdot R_h^{2 / 3} u=kst⋅S1/2⋅Rh2/3
其中,
- u u u 是 ( m / s m / s m/s ) 中的横截面平均流速
- k s t k_{s t} kst 是斯特里克勒系数 ( m 1 / 3 / s m ^{1 / 3} / s m1/3/s ),对应于曼宁 n m n_m nm 的倒数。
- k s t ≈ 20 ( n m ≈ 0.05 ) k_{s t} \approx 20\left(n_m \approx 0.05\right) kst≈20(nm≈0.05) 对于粗糙、复杂和接近自然的河流
- k s t ≈ 90 ( n m ≈ 0.011 ) k_{s t} \approx 90\left(n_m \approx 0.011\right) kst≈90(nm≈0.011) 用于光滑、混凝土内衬的渠道
- k s t ≈ 26 / D 90 1 / 6 k_{s t} \approx 26 / D_{90}^{1 / 6} kst≈26/D901/6 (基于颗粒尺寸 D 90 D_{90} D90 进行近似,其中 90 % 90 \% 90% 的表面沉积物颗粒较小)
- S S S 是假设的能量斜率 ( m / m ) ( m / m ) (m/m),可以假设其对应于稳定、均匀流动条件下的河道斜率。
- R h R_h Rh 是水力半径(米)
水力半径 R h R_h Rh是润湿面积 A A A与润湿周长 P P P的比率。 A A A 和 P P P 都可以作为水深 h h h 和河道底部宽度 b b b 的函数进行计算。许多河道横截面可以近似为梯形,其中水面宽度 B = b + 2 ⋅ h ⋅ m B=b+2 \cdot h \cdot m B=b+2⋅h⋅m(其中 m m m是下图所示的岸坡)。
因此, A A A 和 P P P 由以下公式得出:
A = h ⋅ 0.5 ⋅ ( b + B ) = h ⋅ ( b + h ⋅ m ) P = b + 2 h ⋅ ( m 2 + 1 ) 1 / 2 \begin{gathered} A=h \cdot 0.5 \cdot(b+B)=h \cdot(b+h \cdot m) \\ P=b+2 h \cdot\left(m^2+1\right)^{1 / 2} \end{gathered} A=h⋅0.5⋅(b+B)=h⋅(b+h⋅m)P=b+2h⋅(m2+1)1/2
最后,排水 Q ( m 3 / s ) Q\left( m ^3 / s \right) Q(m3/s)可计算为:
Q = u ⋅ A = k s t ⋅ S 1 / 2 ⋅ R h 2 / 3 ⋅ A Q=u \cdot A=k_{s t} \cdot S^{1 / 2} \cdot R_h^{2 / 3} \cdot A Q=u⋅A=kst⋅S1/2⋅Rh2/3⋅A
编写一个脚本,将流量打印为河道底宽 b b b、岸坡 m m m、水深 h h h、坡度 S S S 和斯特里克勒系数 k s t k_{s t} kst 的函数。
def reversed_mannings_fun(tar, args):Q, b, m_l, m_r, n_m, S_0 = argsarea = ((((tar * m_l) + (tar * m_r) + b) + b) / 2) * tarperimeter = b + (tar * (m_l * m_l + 1) ** 0.5) + (tar * (m_r * m_r + 1) ** 0.5)ratio = area / perimeterreturn (Q * n_m / S_0 ** 0.5) - (area * ratio ** (2.0 / 3.0))def solve(fun, x0, precision, args):last_x = x0next_x = last_x + 10 * precision while abs(last_x - next_x) > precision:next_y = fun(next_x, args)last_x = next_xnext_x = last_x - next_y / derivative(fun, last_x, precision, args) # update estimate using N-Rreturn next_xdef derivative(fun, x, delta_x, args):return (fun(x + delta_x, args) - fun(x - delta_x, args)) / (2.0 * delta_x)if __name__ == '__main__':Q = 15.5 b = 5.1 m_left = 2.5 m_right = 2.5 n_m = 1/20 S_0 = 0.005 init_value = .01 args0 = [Q, b, m_left, m_right, n_m, S_0]x_found = solve(reversed_mannings_fun, init_value, init_value / 10.0, args0)print("Iterated water depth = %.3f" % x_found)🔗参阅:亚图跨际
相关文章:

Python高克勒-曼宁-斯特里克勒公式计算一维流量
📜曼宁公式-用例 📜Python流体数据统计模型和浅水渗流平流模型模拟 | 📜Python蒸发散物理问题(微积分-线性代数-拉普拉斯和傅立叶变换) ✒️Python计算一维流量 高克勒-曼宁-斯特里克勒公式公式基于一维(横截面平均)…...
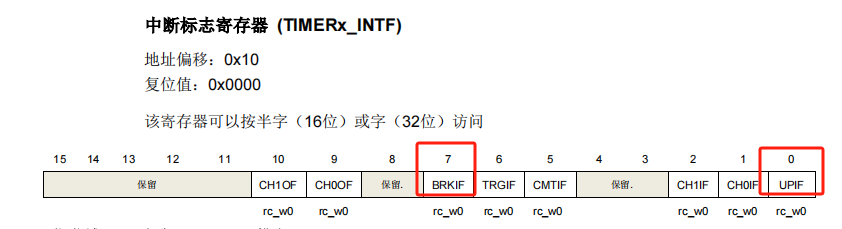
【GD32系列--基本定时器Timer + 定时1ms 灯光间隔1s闪烁例程】
这里写目录标题 一、定时器的作用二、定时器简介1、定时器类型2、时钟树3、定时器功能配置框图 三、定时器寄存器分析1、控制寄存器(TIMERx_CTL0))2、DMA 和中断使能寄存器 (TIMERx_DMAINTEN)3、预分频寄存器 (TIMERx_PSC)4、计数器自动重载寄存器 (TIME…...
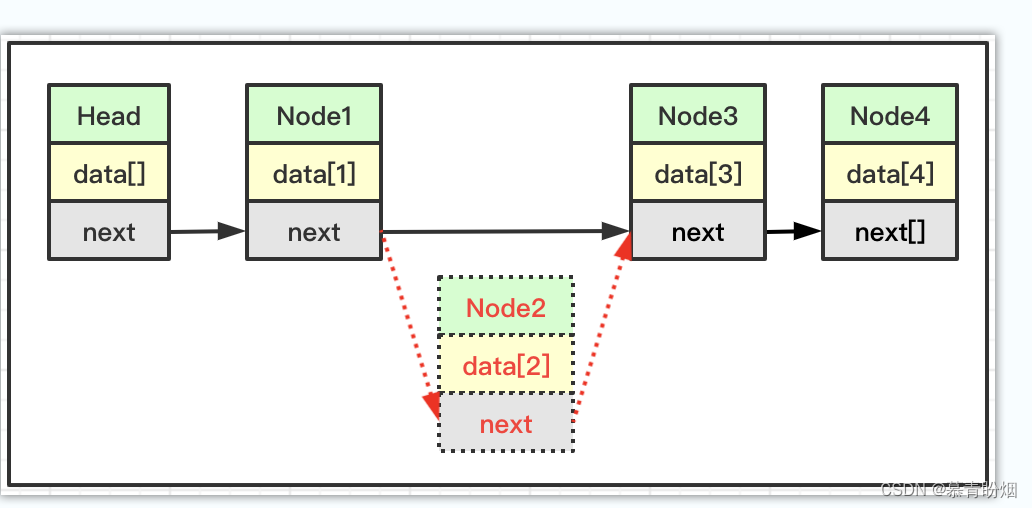
第11章 集合与迭代器
目录 目录 目录 11.1 Collection集合 11.1.1 集合的概念 11.1.2 Collection接口 1、添加元素 2、删除元素 3、查询与获取元素 11.2 List 有序集合 11.2.1 新增方法 11.2.2 ArrayList 11.2.3 LinkedList 1、单向链表 2、双向链表 3、删除元素 11.3 Set 无序集合 …...

探索Linux中的神奇工具:探秘tail命令的妙用
探索Linux中的神奇工具:探秘tail命令的妙用 在Linux系统中,tail命令是一个强大的工具,用于查看文件的末尾内容。本文将详细介绍tail命令的基本用法和一些实用技巧,帮助读者更好地理解和运用这个命令。 了解tail命令 tail命令用…...

1688商品API接口:电商数据自动化的新引擎
1688作为中国领先的B2B电子商务平台,为广大商家和制造商提供了一个展示和交易商品的广阔市场。随着1688商品API接口的推出,开发者和商家现在能够通过编程方式自动化获取和管理商品数据,极大地提高了工作效率和数据处理的灵活性。 一、1688商…...

路由器不能端口映射什么原因?如何设置内网映射?
近期有小伙伴发来求助信息,他以前开游戏服务器和别人一起玩,那个时候端口映射还好,不知道哪一天开始突然不行了,已经是公网了,光猫是桥接的状态,连路由器都换了,就是不能端口映射开服务器&#…...
开源RAG,本地mac启动 dify源码服务
一、Dify文档 参考官方文档来操作,基本没太大的问题。一些细节,我在本篇文章中补充了出来。 这篇文章主要讲以源码的方式启动后端服务,前端服务使用容器启动。 dify 文档地址 欢迎使用 Dify | 中文 | Dify Dify 本地源码部署文档ÿ…...

【Linux取经路】基于信号量和环形队列的生产消费者模型
文章目录 一、POSIX 信号量二、POSIX 信号量的接口2.1 sem_init——初始化信号量2.2 sem_destroy——销毁信号量2.3 sem_wait——等待信号量2.4 sem_post——发布信号量 三、基于环形队列的生产消费者模型3.1 单生产单消费模型3.2 多生产多消费模型3.3 基于任务的多生产多消费模…...
计算机SCI期刊,中科院2区,收稿范围非常广泛!
一、期刊名称 Journal of Web Semantics 二、期刊简介概况 期刊类型:SCI 学科领域:计算机科学 影响因子:2.5 中科院分区:2区 出版方式:开放出版 版面费:$1600 三、期刊征稿范围 《网络语义学杂志》…...

JDK、JRE、编译指令和垃圾回收机制详解
JDK 全称 Java SE Development Kit (Java 开发工具包) JVM虚拟机:Java运行的地方 核心类库:Java提前编好的东西 开发工具: javac,java,jdb,jhat javac:Java编译器,用于将Java源代码编译成Java字节码文件(.class)。 java: java…...

【ARM 嵌入式 C 入门及渐进 6.2 -- ARMv8 C 内嵌汇编读系统寄存器的函数实现】
请阅读【嵌入式开发学习必备专栏】 文章目录 ARMv8 C 内嵌汇编读系统寄存器 ARMv8 C 内嵌汇编读系统寄存器 要在ARMv8架构中通过C代码和内嵌汇编来读取系统寄存器s3_0_c15_c5_5的值,并将其返回,可以按照以下方式实现system_read_reg函数: #…...

使用 LlamaParse 进行 PDF 解析并创建知识图谱
此 Python 笔记本提供了有关利用 LlamaParse 从 PDF 文档中提取信息并随后将提取的内容存储到 Neo4j 图形数据库中的综合指南。本教程在设计时考虑到了实用性,适合对文档处理、信息提取和图形数据库技术感兴趣的开发人员、数据科学家和技术爱好者。 该笔记本电脑的主…...

Oracle行迁移解析
行迁移(Row Migration)是Oracle数据库中的另一个现象,它与行链接类似,都是由于数据行大小的变化导致的存储问题,但其本质和影响有所不同。 触发条件:行迁移发生在当一个已存在的、原先能够完全存储在一个数…...

【k8s】 busybox镜像、挂载volume卷
1. 概述 busybox是一个包含了nslookup,ping,wget等网络处理命令的Pod容器(不含curl命令),它的体积非常小,适合做一些容器内的网络调试。 即创建一个docker ,进去执行 ping 命令等 2. 启动容器 2.1 会自动退出&…...
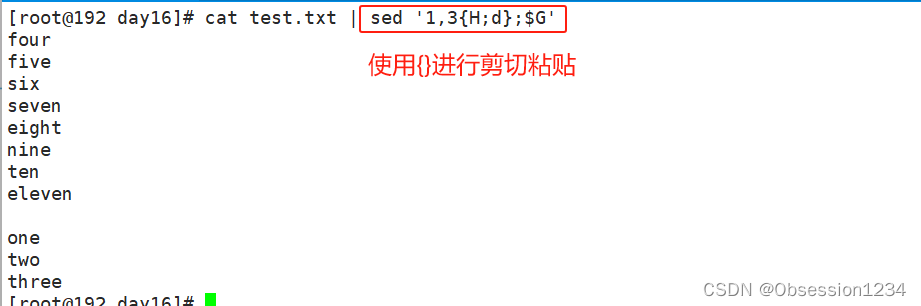
文本三剑客之 sed 编辑器
一.sed 概述 1.sed 介绍 sed是一种流编辑器,流编辑器会在编辑器处理数据之前基于预先提供的一组规则来编辑数据流。 sed编辑器可以根据命令来处理数据流中的数据,这些命令要么从命令行中输入,要么存储在一个 命令文本文件中。 2.sed 的工…...
-查询优化(3)-索引合并)
【MySQL精通之路】SQL优化(1)-查询优化(3)-索引合并
主博客: 【MySQL精通之路】SQL优化(1)-CSDN博客 上一篇: 【MySQL精通之路】SQL优化(1)-查询优化(2)-范围查询优化-CSDN博客 下一篇: 目录 1.索引合并-交集访问算法 2.索引合并联合访问算法 3.索引合并-排序联合访问算法 4.影响索引合…...
)
Linux中安装配置并使用samba服务(Centos以及Ubuntu)
目录 前言1. 基本知识2. Centos3. Ubuntu3.1 物理服务器3.2 云服务器前言 在window与linux系统中配置一个共享文件夹,可以做很多时间,比如映射器或者像linux中定时存放文件等 1. 基本知识 在Ubuntu上安装和配置Samba服务可以让你的Ubuntu机器与Windows、macOS以及其他Linu…...

three.js能实现啥效果?看过来,这里都是它的菜(06)
这是第五期了,本期继续分享three.js可以实现的3D动画案例,有老铁反馈再发案例的时候,是否可以顺道分享一下three.js的知识点,好吧,安排。 材质动画 材质动画可以实现各种复杂的视觉效果,包括但不限于以下…...

利用ESP32-C3将TF卡内容变成U盘进行读取
利用ESP32-C3将TF卡内容变成U盘进行读取 ESP32-C3是一款高性价比的微控制器,具备WiFi和蓝牙功能,广泛应用于物联网(IoT)项目中。除了常见的无线通信功能外,ESP32-C3还可以用来模拟U盘读取TF卡内容。本文将介绍如何通过…...

C++小病毒
C小病毒(注:对电脑无过大伤害) 短短行,创造奇迹! 把这个文件命名为virus.exe就可以使用了。 #include<bits/stdc.h> #include<windows.h> using namespace std; int main() {HWND hwnd GetForegroundW…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

归并排序:分治思想的高效排序
目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法,由约翰冯诺伊曼在1945年提出。其核心思想包括: 分割(Divide):将待排序数组递归地分成两个子…...
