【线性回归】梯度下降
文章目录
- @[toc]
- 数据
- 数据集
- 实际值
- 估计值
- 梯度下降算法
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 结果可视化
- 完整代码
- 结果可视化
- 线性拟合结果
- 代价变化
文章目录
- @[toc]
- 数据
- 数据集
- 实际值
- 估计值
- 梯度下降算法
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 结果可视化
- 完整代码
- 结果可视化
- 线性拟合结果
- 代价变化
数据
数据集
( x ( i ) , y ( i ) ) , i = 1 , 2 , ⋯ , m \left(x^{(i)} , y^{(i)}\right) , i = 1 , 2 , \cdots , m (x(i),y(i)),i=1,2,⋯,m
实际值
y ( i ) y^{(i)} y(i)
估计值
h θ ( x ( i ) ) = θ 0 + θ 1 x ( i ) h_{\theta}\left(x^{(i)}\right) = \theta_{0} + \theta_{1} x^{(i)} hθ(x(i))=θ0+θ1x(i)
梯度下降算法
估计误差
h θ ( x ( i ) ) − y ( i ) h_{\theta}\left(x^{(i)}\right) - y^{(i)} hθ(x(i))−y(i)
代价函数
J ( θ ) = J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 J(\theta) = J(\theta_{0} , \theta_{1}) = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)^{2}} = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(\theta_{0} + \theta_{1} x^{(i)} - y^{(i)}\right)^{2}} J(θ)=J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1i=1∑m(θ0+θ1x(i)−y(i))2
学习率
- α \alpha α是学习率,一个大于 0 0 0的很小的经验值,决定代价函数下降的程度
参数更新
Δ θ j = ∂ ∂ θ j J ( θ 0 , θ 1 ) \Delta{\theta_{j}} = \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) Δθj=∂θj∂J(θ0,θ1)
θ j : = θ j − α Δ θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j} := \theta_{j} - \alpha \Delta{\theta_{j}} = \theta_{j} - \alpha \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) θj:=θj−αΔθj=θj−α∂θj∂J(θ0,θ1)
$$
\left[
\begin{matrix}
\theta_{0} \
\theta_{1}
\end{matrix}
\right] :=
\left[
\begin{matrix}
\theta_{0} \
\theta_{1}
\end{matrix}
\right] -
\alpha
\left[
\begin{matrix}
\cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \
\cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}}
\end{matrix}
\right]
$$
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] e ( i ) = h θ ( x ( i ) ) − y ( i ) \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right) x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] \kern{2em} e^{(i)} = h_{\theta}\left(x^{(i)}\right) - y^{(i)} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑m(hθ(x(i))−y(i))m1i=1∑m(hθ(x(i))−y(i))x(i) = m1i=1∑me(i)m1i=1∑me(i)x(i) e(i)=hθ(x(i))−y(i)
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] = [ 1 m ( e ( 1 ) + e ( 2 ) + ⋯ + e ( m ) ) 1 m ( e ( 1 ) x ( 1 ) + e ( 2 ) x ( 2 ) + ⋯ + e ( m ) x ( m ) ) ] = 1 m [ 1 1 ⋯ 1 x ( 1 ) x ( 2 ) ⋯ x ( m ) ] [ e ( 1 ) e ( 2 ) ⋮ e ( m ) ] = 1 m X T e = 1 m X T ( X θ − y ) \begin{aligned} \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] &= \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) \\ \cfrac{1}{m} \left(e^{(1)} x^{(1)} + e^{(2)} x^{(2)} + \cdots + e^{(m)} x^{(m)}\right) \end{matrix} \right] \\ &= \cfrac{1}{m} \left[ \begin{matrix} 1 & 1 & \cdots & 1 \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \end{matrix} \right] \left[ \begin{matrix} e^{(1)} \\ e^{(2)} \\ \vdots \\ e^{(m)} \end{matrix} \right] = \cfrac{1}{m} X^{T} e = \cfrac{1}{m} X^{T} (X \theta - y) \end{aligned} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑me(i)m1i=1∑me(i)x(i) = m1(e(1)+e(2)+⋯+e(m))m1(e(1)x(1)+e(2)x(2)+⋯+e(m)x(m)) =m1[1x(1)1x(2)⋯⋯1x(m)] e(1)e(2)⋮e(m) =m1XTe=m1XT(Xθ−y)
- 由上述推导得
Δ θ = 1 m X T e \Delta{\theta} = \cfrac{1}{m} X^{T} e Δθ=m1XTe
θ : = θ − α Δ θ = θ − α 1 m X T e \theta := \theta - \alpha \Delta{\theta} = \theta - \alpha \cfrac{1}{m} X^{T} e θ:=θ−αΔθ=θ−αm1XTe
Python实现
导包
import numpy as np
import matplotlib.pyplot as plt
数据预处理
x = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones((m, 1)), x]
y = y.reshape(m, 1)
迭代过程
alpha = 0.01 # 学习率
iter_cnt = 1000 # 迭代次数
cost = np.zeros(iter_cnt) # 代价数据
theta = np.zeros((2, 1))for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# cost[i] = 1 / (2 * m) * np.sum(np.square(error)) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta
结果可视化
# 线性拟合结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.savefig('../pic/fit.png')
plt.show()# 代价结果
plt.plot(cost)
plt.savefig('../pic/cost.png')
plt.show()
完整代码
import numpy as np
import matplotlib.pyplot as pltx = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones((m, 1)), x]
y = y.reshape(m, 1)alpha = 0.01 # 学习率
iter_cnt = 1000 # 迭代次数
cost = np.zeros(iter_cnt) # 代价数据
theta = np.zeros((2, 1))for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# cost[i] = 1 / (2 * m) * np.sum(np.square(error)) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta# 线性拟合结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.savefig('../pic/fit.png')
plt.show()# 代价结果
plt.plot(cost)
plt.savefig('../pic/cost.png')
plt.show()
结果可视化
线性拟合结果

代价变化

相关文章:

【线性回归】梯度下降
文章目录 [toc]数据数据集实际值估计值 梯度下降算法估计误差代价函数学习率参数更新 Python实现导包数据预处理迭代过程结果可视化完整代码 结果可视化线性拟合结果代价变化 数据 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , y^{(i)}\right) , i 1 ,…...

GMSL图像采集卡,适用于无人车、自动驾驶、自主机器、数据采集等场景,支持定制
基于各种 系列二代 G MS L 图像采集卡(以下简称 二代图像采集卡)是一款自主研发的一款基于 F P G A 的高速图像产品,二代图像采集卡相比一代卡,由于采用PCIe G en 3 技术,速度和带宽都相应的有了成 倍的提高。该图像…...

docker不删除容器更改其挂载目录
场景:docker搭建的jenkins通常需要配置很多开发环境,当要更换挂载目录,每次都需要删除容器重新运行,不在挂载目录的环境通常不会保留。 先给一个参考博客docker不删除容器,修改容器挂载或其他_jenkins 修改容器挂载do…...
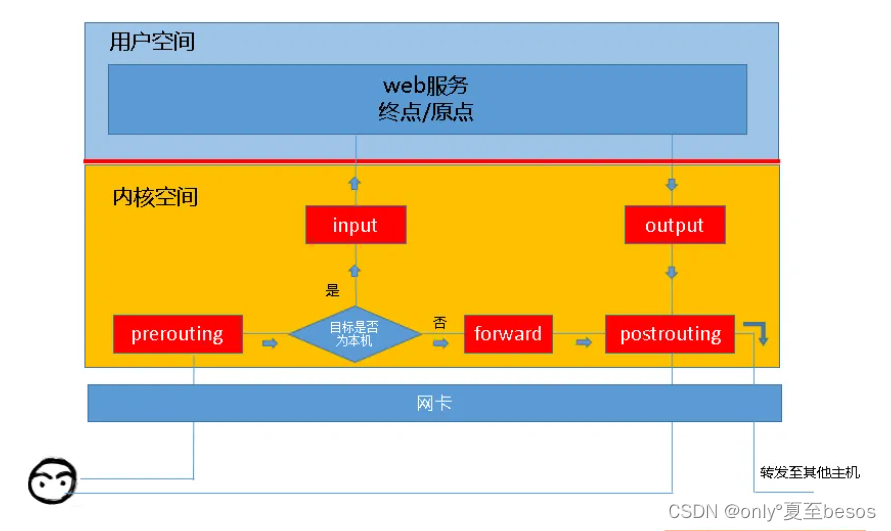
K8s Service 背后是怎么工作的?
kube-proxy 是 Kubernetes 集群中负责服务发现和负载均衡的组件之一。它是一个网络代理,运行在每个节点上, 用于 service 资源的负载均衡。它有两种模式:iptables 和 ipvs。 iptables iptables 是 Linux 系统中的一个用户空间实用程序,用于…...
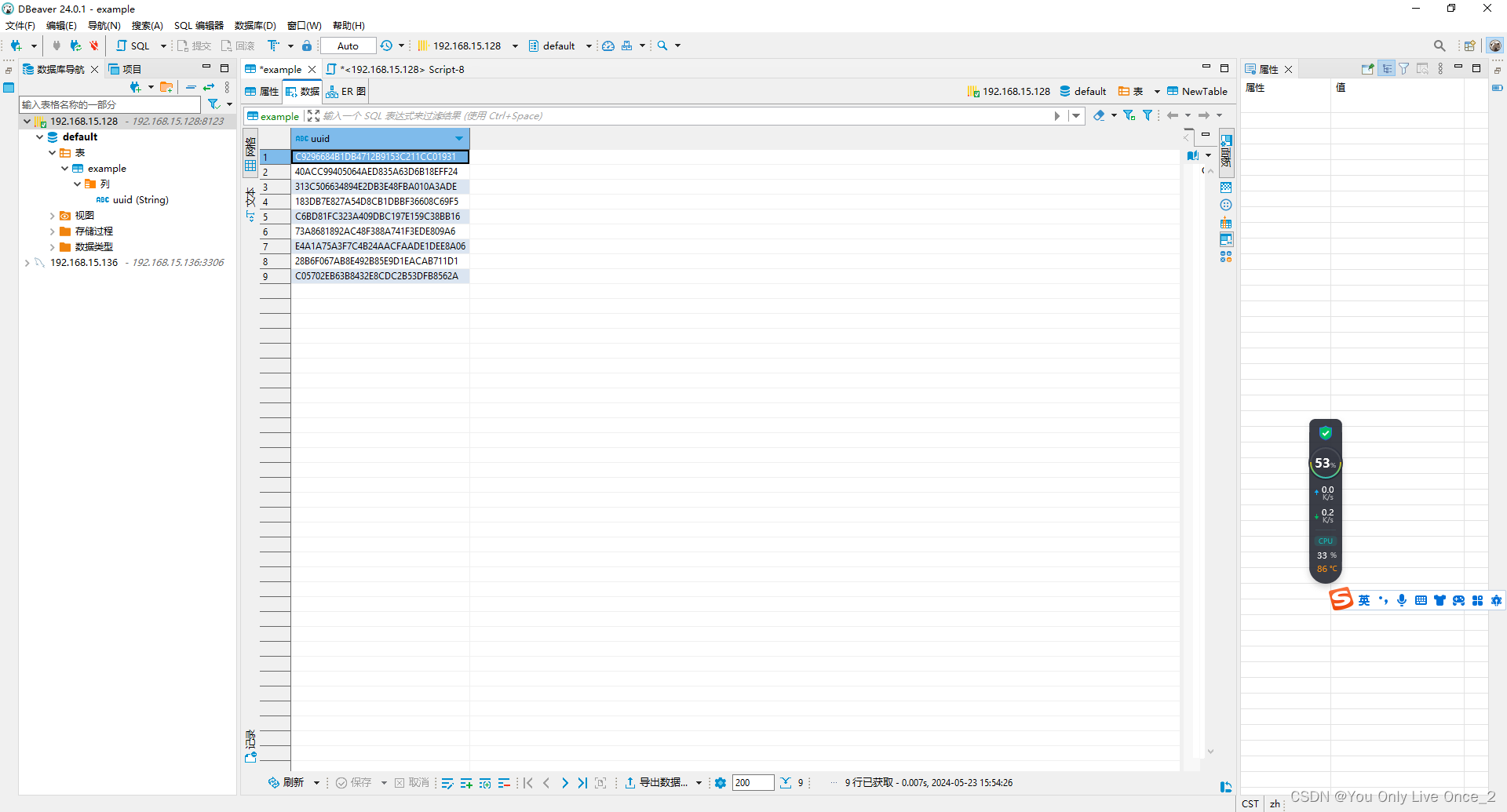
ClickHouse配置与使用
静态IP配置 # 修改网卡配置文件 vim /etc/sysconfig/network-scripts/ifcfg-ens33# 修改文件内容 TYPEEthernet PROXY_METHODnone BROWSER_ONLYno BOOTPROTOstatic IPADDR192.168.18.128 NETMASK255.255.255.0 GATEWAY192.168.18.2 DEFROUTEyes IPV4_FAILURE_FATALno IPV6INIT…...

将某一个 DIV 块全屏展示
文章目录 需求分析 需求 上节我们研究了如何将页面中的指定 div 下载为图片:跳转查看 本节演技一下如何将 DIV 全屏展示 全屏展示某一个 DIV 分析 其实就是模拟键盘动作 F11 var element document.getElementById(pic) var requestMethod element.requestFullS…...

K8S集群再搭建
前述:总体是非常简单的,就是过程繁琐,不过都是些重复的操作 master成员: [controller-manager, scheduler, api-server, etcd, proxy,kubelet] node成员: [kubelet, proxy] master要修改的配置文件有 1. vi /etc/etcd/etcd.conf # 数…...

工具-博客搭建
以下相关讲解均基于hexo github pages方案,请注意!!!博客搭建方案选择 参考文章1 搭建教程 参考文章1 hexo github pages搭建过程中遇到的问题 删除categories、tags 1、删除含有需要删除categories、tags的文章 2、hexo …...

贪心算法:合并区间
参考资料:代码随想录 题目链接:. - 力扣(LeetCode) 做过用最少数量的箭引爆气球和无重叠区间这两道题目后,题意和题解都不难理解。唯一的一点儿难点是对于api的运用。 class Solution {public int[][] merge(int[][…...

DFA 算法
为什么要学习这个算法 前一段时间遇到了瓶颈,因为词库太多了导致会有一些速度过慢,而且一个正则表达式已经放不下了,需要进行拆分正则才可以。 正好我以前看过有关 dfa 的介绍,但是并没有深入的进行研究,所以就趁着周…...

Web(数字媒体)期末作业
一.前言 1.本资源为类似于打飞机的网页游戏 2.链接如下:【免费】前端web或者数字媒体的期末作业(类似于打飞机的2D网页小游戏)资源-CSDN文库 二.介绍文档...

展现金融科技前沿力量,ATFX于哥伦比亚金融博览会绽放光彩
不到半个月的时间里,高光时刻再度降临ATFX。而这一次,是ATFX不曾拥有的桂冠—“全球最佳在线经纪商”(Best Global Online Broker)。2024年5月15日至16日,拉丁美洲首屈一指的金融盛会—2024年哥伦比亚金融博览会(Money Expo Colombia 2024) 于…...
、元素rem实现自适应)
html 根字号 以及 设置根元素font-size:calc(100vw/18.75)、元素rem实现自适应
rem 单位介绍:rem 是相对文档根元素(html)字体大小的尺寸单位,当元素的尺寸或文字字号等使用 rem 单位时,会随着根元素的 font-size变化而变化。 得出结论:在不同分辨率的设备下动态设置根元素的字体大小就可以实现页面自适应。 …...

size_t无符号数相关知识点
size_t无符号数相关知识点 在代码编译的时候,报错一个warning: comparison between signed and unsigned interger expression [-wsign-compare] 找到代码,告警这一段代码 size_t count timeProtocol.m_intersectionArray.size(); for (u…...
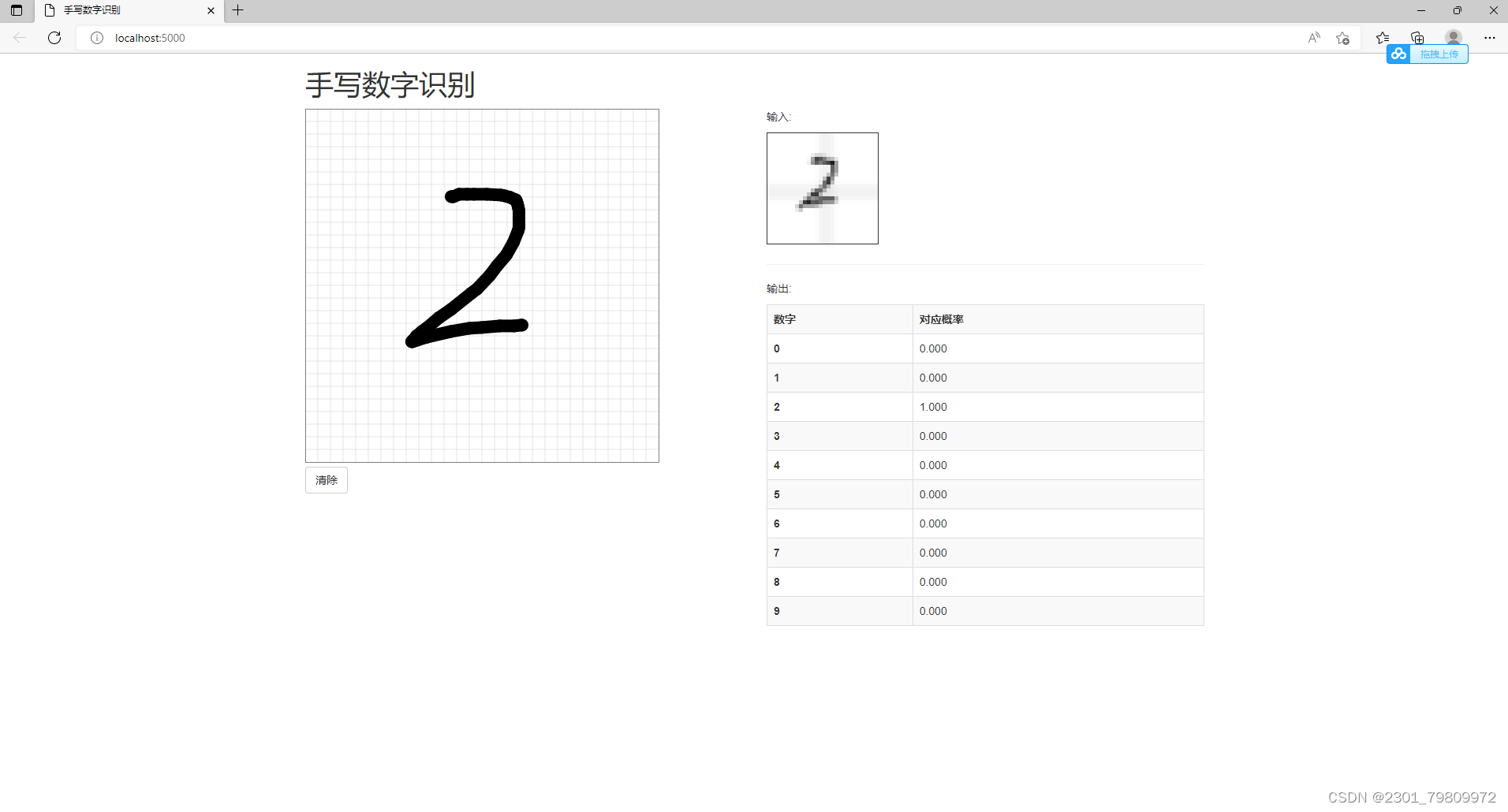
深度学习之基于Tensorflow+Flask框架Web手写数字识别
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 一、项目背景与意义 手写数字识别是深度学习领域中的一个经典问题,也是计算机视觉领域的重要应用之一。…...

2024电工杯B题食谱评价与优化模型思路代码论文分析
2024年电工杯数学建模竞赛B题论文和代码已完成,代码为B题全部问题的代码,论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解(问题1模型的建立和求解、问题2模型的建立和求解、问题3模型的建立和求解)、模型…...
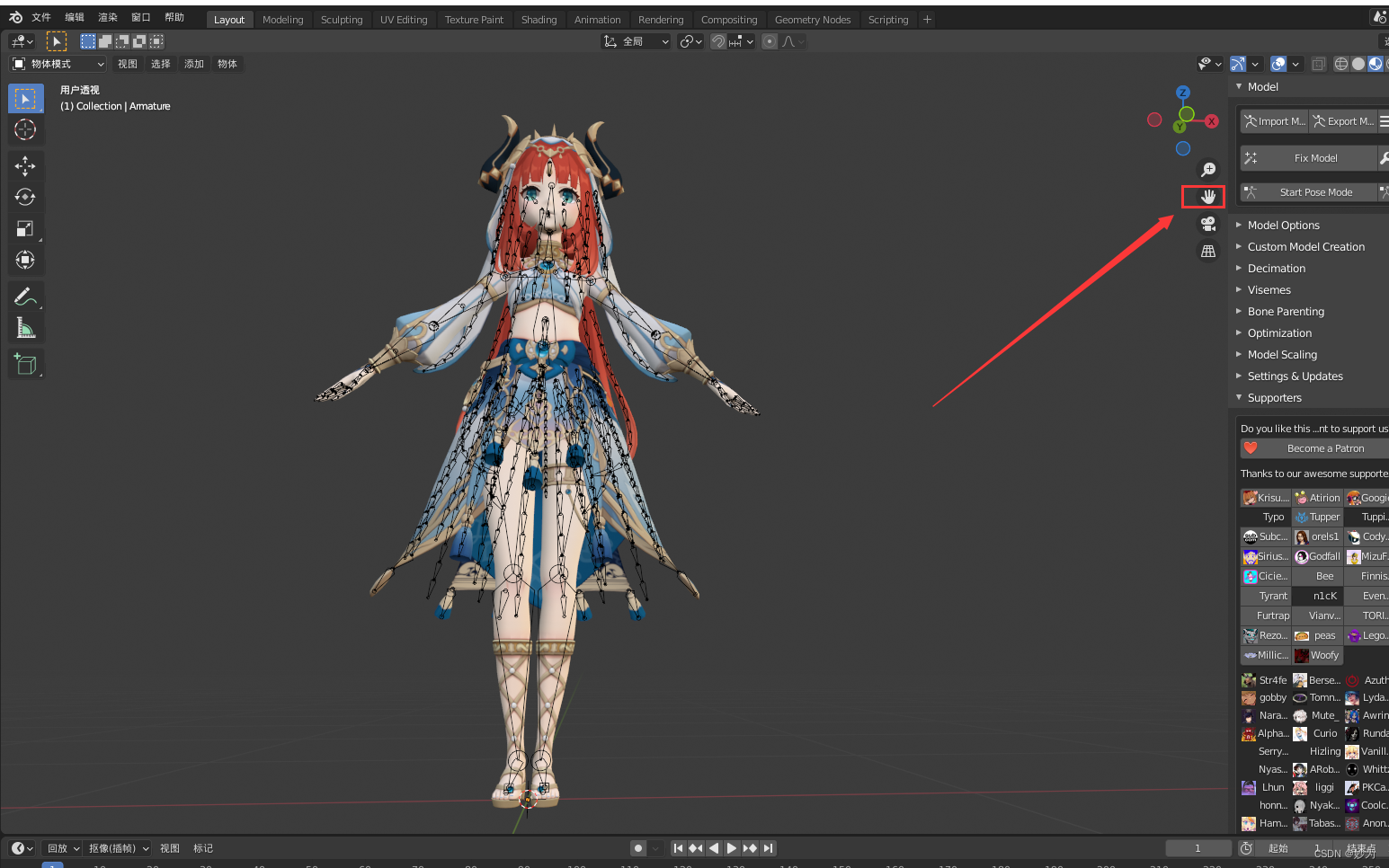
blender安装cats-blender-plugin-0-19-0插件,导入pmx三维模型
UE5系列文章目录 文章目录 UE5系列文章目录前言一、Blender安装二、cats-blender-plugin-0-19-0插件下载三、下载bmp文件四、在blender2.93中安装cats-blender-plugin-0-19-0插件 前言 blender本身不支持pmx三维模型,需要用到cats-blender-plugin-0-19-0插件。 一…...

[源码+搭建教程]西游伏妖篇手游_GM_单机+和朋友玩
为了学习和研究软件内含的设计思想和原理,本人花心血和汗水带来了搭建教程!!! 教程不适于服架设,严禁服架设!!!请牢记!!! 教程仅限学习使用&…...
windows、mac、linux中node版本的切换(nvm管理工具),解决项目兼容问题 node版本管理、国内npm源镜像切换
文章目录 在工作中,我们可能同时在进行2个或者多个不同的项目开发,每个项目的需求不同,进而不同项目必须依赖不同版本的NodeJS运行环境,这种情况下,对于维护多个版本的node将会是一件非常麻烦的事情,nvm就是…...

【MySQL精通之路】全文搜索-布尔型全文搜索
1.使用方法 MySQL可以使用IN BOOLEAN MODE修饰符执行布尔全文搜索。 使用此修饰符,某些字符在搜索字符串中单词的开头或结尾具有特殊含义。 在下面的查询中,和-运算符分别表示单词必须存在或不存在,才能进行匹配。 因此,查询检…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
