matlab在管理学中的应用简matlab基础【三】
规划论及MATLAB计算
1、线性规划
问题的提出
例1. 某工厂在计划期内要安排甲、乙两种产品的生产,已知生产单位产品所需的资源A、B、C的消耗以及资源的计划期供给量,如下表:
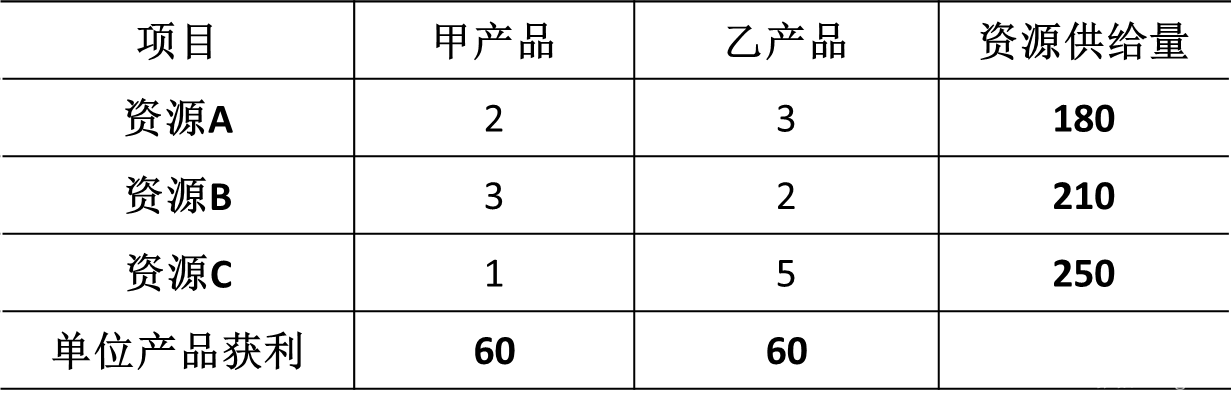 问题:工厂应分别生产多少单位甲、乙产品才能使工厂获利最多?
问题:工厂应分别生产多少单位甲、乙产品才能使工厂获利最多?
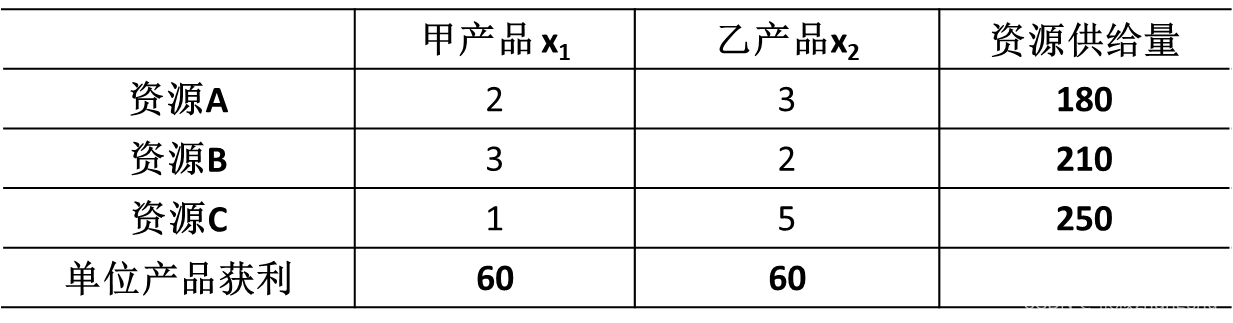
解:设 甲、乙产品的产量分别为x1、x2 ,
工厂获利为 z , 则
目标函数:
Max z = 60x1 + 60x2
约束条件:s.t.
2 x1 + 3 x2 ≤ 180
3 x1 + 2 x2 ≤ 210
x1 + 5 x2 ≤ 250
x1 , x2 ≥ 0
从上述的例子看出,建立数学模型的基本过程是:
1)搞清要解决的问题:目标 和 条件;
2)设置决策变量–描述解决问题的方案;
3)描述约束条件和非负约束;
4)给出目标函数,确定目标函数的优化方向,即优化是对目标函数取最大还是最小。
(2)线性规划模型:一般形式
目标函数:
Max(Min)z = c1 x1 + c2 x2 + … + cn xn
约束条件:s.t.
a11 x1 + a12 x2 + … + a1n xn ≤( =, ≥ )b1
a21 x1 + a22 x2 + … + a2n xn ≤( =, ≥ )b2
…… ……
am1 x1 + am2 x2 + … + amnxn ≤( =, ≥ )bm
x1 ,x2 ,… ,xn ≥ 0
线性规划一般数学模型的矩阵形式
目标函数 max(或min) z=c·x
约束条件 A·x≤ ( =, ≥ ) b
x≥0
式中 c=(c1,c2,…,cn), x=(x1,x2,…,xn)τ
a11 a12 … a1n
A= a21 a22 … a2n , b=(b1,b2,…,bm)τ… am1 am2 … amn
3)线性规划模型:标准形式
目标函数:
Max z = c1 x1 + c2 x2 + … + cn xn
约束条件:s.t.
a11 x1 + a12 x2 + … + a1n xn =b1
a21 x1 + a22 x2 + … + a2n xn =b2
…… ……
am1 x1 + am2 x2 + … + amnxn =bm
x1 ,x2 ,… ,xn ≥ 0
线性规划标准型的矩阵形式
目标函数 max z=c·x
约束条件 A·x = b
x≥0
式中 c=(c1,c2,…,cn), x=(x1,x2,…,xn)τ
a11 a12 … a1n
A= a21 a22 … a2n , b=(b1,b2,…,bm)τ… am1 am2 … amn
(4)线性规划的图解法
目标函数:
max Z= X1 + X2
约束条件:
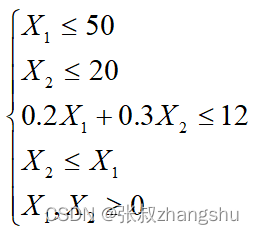
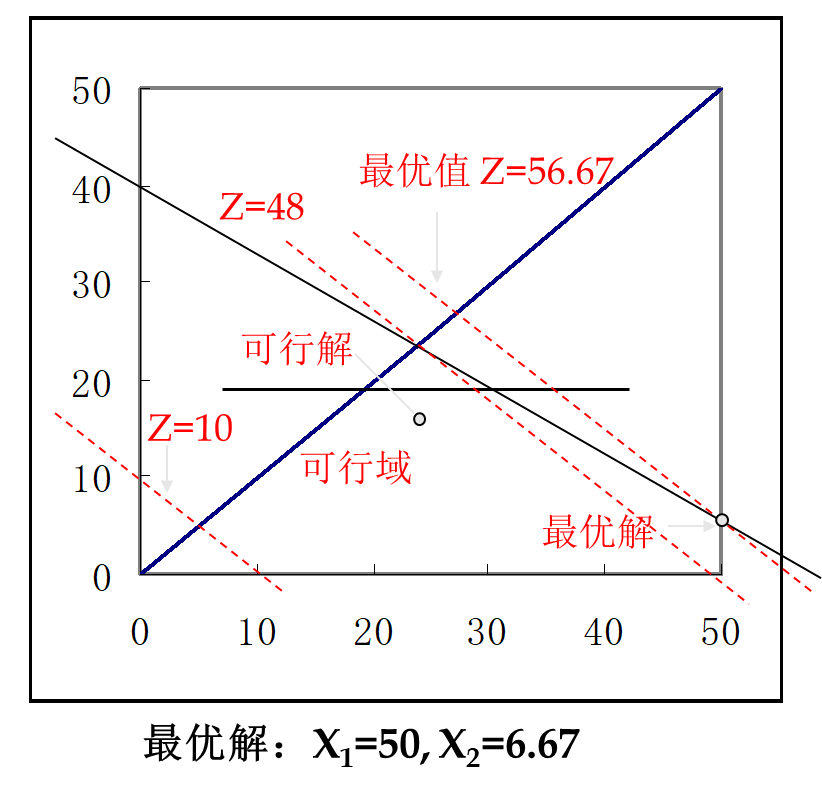
例1 的图解
目标函数:
Max z = 60 x1 + 60 x2
约束条件:
2 x1 + 3 x2 ≤ 180 (A)
3 x1 + 2 x2 ≤ 210 (B)
x1 + 5 x2 ≤ 250 ©
x1 , x2 ≥ 0 (D)
得到最优解:
x1 = 54, x2 = 24
最优目标值 z = 4680
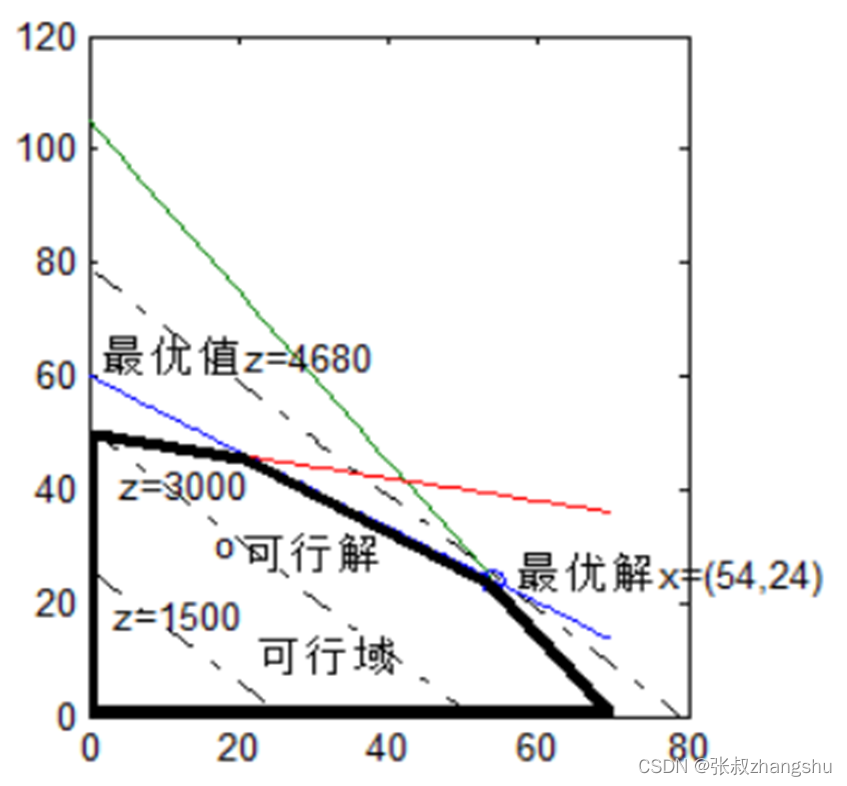
解的几种情况:
线性规划的最优解如果存在
则必定有一个顶点(极点)是最优解
① 唯一解
目标函数等值线与约束边界只有一个交点
② 无穷多最优解
目标函数等值线与约束边界平行
③ 无界解
可行域不封闭
④ 无可行解
可行域为空集
(5)线性规划解的概念
引入松驰变量____含义是资源的剩余量
例1 中引入 s1, s2, s3 模型化为 标准型
目标函数:Max z = 60 x1 + 60 x2 + 0 s1 + 0 s2 + 0 s3
约束条件:s.t. 2 x1 + 3 x2 + s1 = 180
3 x1 + 2 x2 + s2 = 210
x1 + 5 x2 + s3 = 250
x1 , x2 , s1 , s2 , s3 ≥ 0
对于标准型的最优解 x1 =54 x2 = 24 , s1 = 0 s2 = 0 s3 = 76
说明:生产54单位甲产品和24单位乙产品将消耗完所有的A、B资源,但对资源C则还剩余76。
基最优解、最优解、基可行解、基解、可行解的关系如下所示:

(6)线性规划的基本定理
① 线性规划问题的所有可行解构成的集合(可行域)
R={x|A·x=b,x≥0}
R是一凸集(包括无界域),它有有限个顶点;
② 线性规划问题的每个基可行解
对应可行域凸集R的一个顶点;
③ 若线性规划问题有最优解,
则必定在某顶点处得到
基本定理把可行域的有限个顶点与基可行解这一代数概念联系起来,可通过求基可行解的代数方法来得到可行域的一切极点,能在有限的计算中获得最优点。
相关文章:

matlab在管理学中的应用简matlab基础【三】
规划论及MATLAB计算 1、线性规划 问题的提出 例1. 某工厂在计划期内要安排甲、乙两种产品的生产,已知生产单位产品所需的资源A、B、C的消耗以及资源的计划期供给量,如下表: 问题:工厂应分别生产多少单位甲、乙产品才能使工厂获…...
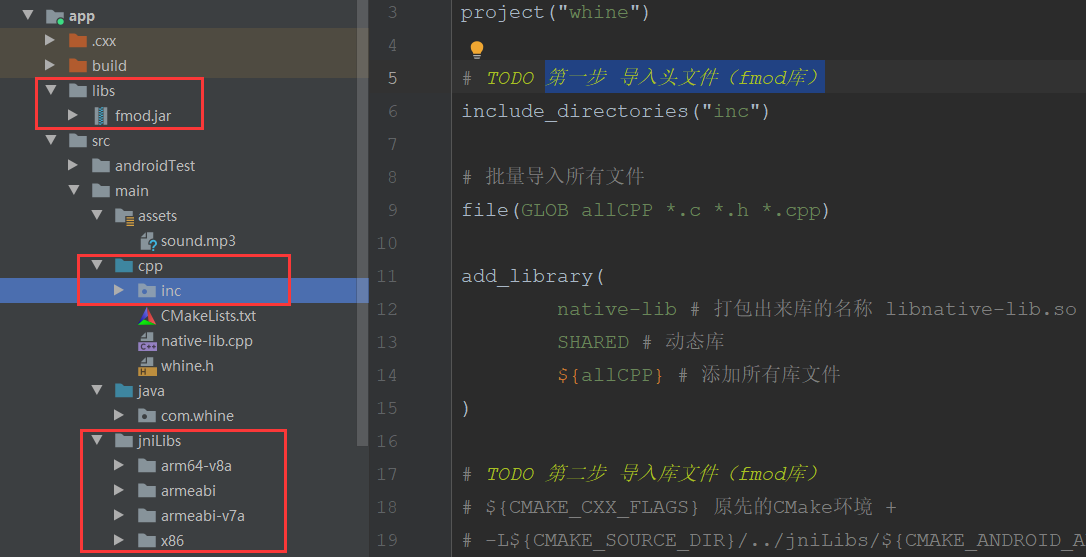
NDK JNI 变声器实现
Android NDK 导入 C库的开发流程学习;通过使用fmod的C库,实现变声器功能。导入库文件1)复制fmod的C库到cpp目录下2)复制fmod的so库到jniLibs目录下3)复制fmod的jar库到libs目录下4)将声音文件复制到assets目…...

VMLogin防关联指纹浏览器的主帐号和子账号区别介绍
VMLogin主账户管理子账户,主要用于团队协作,分账户登录使用,主账户相当于老板,子账户相当于员工。 主账户创建并管理子账户; 主账户可以修改子账户的密码; 主账户可以设置子账户是否有创建配置文件权限&a…...

Apache DolphinScheduler GitHub Star 突破 10000!
点击蓝字 关注我们今天,Apache DolphinScheduler GitHub Star 突破 10000,项目迎来一个重要里程碑。这表明 Apache DolphinScheduler 已经在全球的开发者和用户中获得了广泛的认可和使用。DolphinScheduler 旨在解决公司日常运营中的大数据处理工作流调度…...

程序员中的女性力量——做不被定义的自己
她是office lady,亦是程序媛,程序员界的靓丽色彩,不可或缺。 “只有那些疯狂到以为自己能够改变世界的人——才能真正改变世界。” 女性该如何定义自己?程序媛怎么发挥自己最大的价值。 争取自己做选择,经济和思想都独…...

pb中Datawindow中每页打印固定行
Datawindow中每页打印固定行 第一步: 增加一个计算列,此计算列必须放在Detail段,Expression中输入:ceiling(getrow()/20),这里20还可以用全局函数取代,这样可以允许用户任意设置每页打印多少行。 第二步: 定义分组,选择菜单Rows->Create Group...按计算列字段…...
【独家】)
华为OD机试 - 内存池(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:内存池题…...

SaaS简介
SaaS 简介 SaaS被认为是云计算的一部分,其他包括基础设施即服务(IaaS)、平台即服务(PaaS)、桌面即服务(DaaS)、托管软件即服务(MSaaS)、移动后端即服务(MBaaS)、数据中心即服务(DCaaS)、集成平台即服务(iPaaS)和信息技术管理即服务(ITMaaS) SaaS应用程序通常由web浏…...

unity 实现使用三张图片来表达车速,通过传值达到车速
//速度 public Image SpeedNums_Unit; public Image SpeedNums_Ten; //public Image SpeedNums_Hundred; //kw public Image MileageNums_Unit; public Image MileageNums_Ten; /// /// 仪表速度UI /// private void SpeedUI(string speedStr) {if (SpeedNums_Unit == null) …...
程序员看过都说好的资源网站,你值得拥有。
程序员必备的相关资源网站一.技术社区1.GitHub2.Gitee(码云)3.稀土掘金4.OSCHINA开源中国5.CSDN6.博客园7.SegmentFault(思否)8.Stack Overflow9.Golang中文社区10.ChinaUnix11.51CTO12.Ruby China二.技术教程1.Devdocs2.码农教程…...

【MySQL高级篇】第03章 用户与权限管理
第03章 用户与权限管理 1. 用户管理 1.1 登录MySQL服务器 启动MySQL服务后,可以通过mysql命令来登录MySQL服务器,命令如下: mysql –h hostname|hostIP –P port –u username –p DatabaseName –e "SQL语句"-h参数后面接主机…...
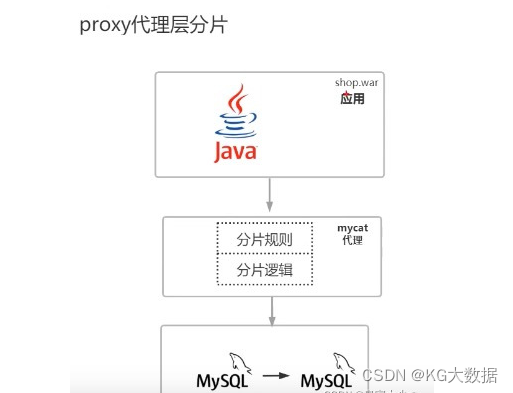
MySQL的分库分表?通俗易懂
1- 为什么要分库分表 如果一个网站业务快速发展,那这个网站流量也会增加,数据的压力也会随之而来,比如电商系统来说双十一大促对订单数据压力很大,Tps十几万并发量,如果传统的架构(一主多从)&a…...

elasticsearch 查询语法
match_all 查询所有 GET test/_search {"query": {"match_all": {}} }match 单字段匹配查询 GET test/_search {"query":{"match":{"name":"zhangsan"}} }multi_match 多字段匹配查询 GET test/_search {"…...

深入剖析MVC模型与三层架构
MVC(Model-View-Controller)模型和三层架构都是常见的软件架构模式,用于实现大型应用程序和软件系统。下面是对它们的深入剖析: MVC模型 MVC模型是一种将应用程序分成三个主要组件的软件架构模式,分别是模型…...

使用 Wall 搭建个人照片墙和视频墙
下载 Github:https://github.com/super-tongyao/wall 国内仓库(不推荐,只做加速访问,无编译包和发行版,以github仓库为准):https://gitee.com/Super_TongYao/wall 推荐github仓库,下载最新版…...

03_Linux压缩解压,用户用户组,文件权限
目录 Linux下常用的压缩格式 gzip 压缩工具 gzip 对文件夹进行压缩 bzip2 压缩工具 tar打包工具 对.tar.bz2 进行压缩和解压缩 对.tar.gz 进行压缩和解压缩 rar格式 zip格式 Linux用户 Linux用户组 创建用户和用户组 Linux文件权限 Linux文件权限修改 Linux下常用…...
硬盘分区数据恢复?这些方法助您解忧
案例:分区把电脑文件丢了,数据还能恢复吗? “急急急!!!本人电脑小白,在使用磁盘管理合并E、F分区的时候,不小心把D分区给删除了,D分区里面存放了很多重要的数据与文件&a…...
高校竞赛信息管理系统
摘要随着当今社会的发展,时代的进步,各行各业也在发生着变化,比如高校竞赛信息管理这一方面,利用网络已经逐步进入人们的生活。传统的高校竞赛信息管理,都是学生去学校查看竞赛信息然后再进行报名,这种传统…...

还是要学好数学啊
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:第一分钟,将任一格子染成蓝色。之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。下图分别是 1、2、…...
ActiveMQ反序列化漏洞原理+复现
ActiveMQ反序列化漏洞 ActiveMQ ActiveMQ是开源消息总线,消息中间件 工作原理 通过使用消息队列,实现服务的异步处理,主要目的是减少请求响应时间和解耦合。 消息队列,服务器A将客户发起的请求放入服务器B的消息队列中&#…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
