二叉树顺序结构及链式结构
一.二叉树的顺序结构
1.定义:使用数组存储数据,一般使用数组只适合表示完全二叉树,此时不会有空间的浪费
注:二叉树的顺序存储在逻辑上是一颗二叉树,但是在物理上是一个数组,此时需要程序员自己想清楚调整数据时应该怎样调整
2.堆
(1)定义:集合中所有元素按照完全二叉树的顺序存储在一个一维数组中,并满足Ki<=K2*i+1且K2*i+2(或Ki<=K2*i+1且K2*i+2)的规律,则称之为堆

(2)性质:
1>堆中某个节点的值总是不大于(或不小于)其父节点的值
2>堆是一颗完全二叉树
3>大堆:任何一个父节点的值>=孩子的值
小堆:任何一个父节点的值<=孩子的值
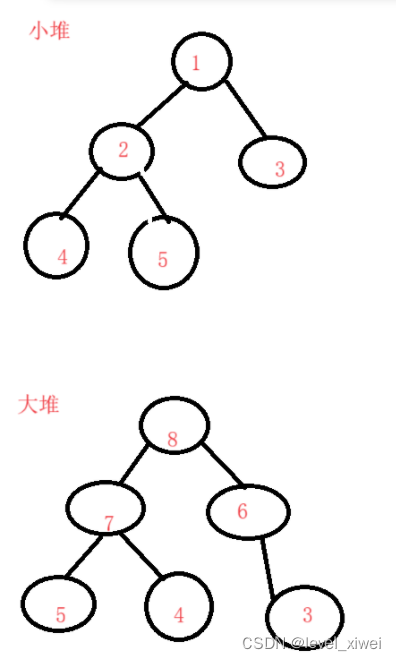
(3)堆的实现(以小堆为例)
1>堆的结构体定义:数组指针(用于存储数据),有效数据个数,空间容量大小
typedef int HeapDataType;
typedef struct Heap
{HeapDataType* a;//数组指针int size;//有效数据个数int capacity;//有效空间大小
}HP;
2>堆的初始化:
//堆的初始化
void HPInit(HP* ph)
{assert(ph);ph->a = NULL;ph->size = ph->capacity = 0;
}
3>堆的销毁:
//堆的销毁
void HPDestory(HP* ph)
{assert(ph);free(ph->a);ph->a = NULL;ph->size = ph->capacity = 0;
}4>向堆中插入数据:
**思路:将数据插在原数据的最后面,在不断向上调整以保证插入数据后仍为小堆
**画图解释
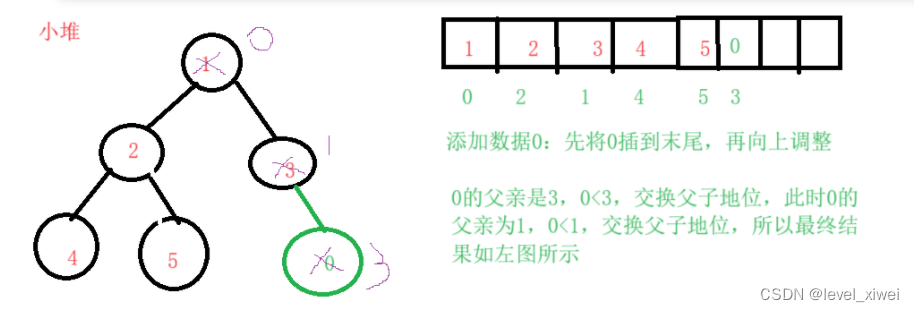
**代码实现
//向堆内插入数据
void HPPush(HP* ph, HeapDataType x)
{assert(ph);//判断是否需要增容if (ph->size == ph->capacity){int newcapacity = ph->capacity * 2 == 0 ? 4 : ph->capacity * 2;HeapDataType* tmp = (HeapDataType*)realloc(ph->a, sizeof(HeapDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}ph->a = tmp;ph->capacity = newcapacity;}ph->a[ph->size] = x;ph->size++;AdjustUp(ph->a, ph->size-1);}
5>向上调整数据:
思路:找孩子的父亲,判断父亲是否大于孩子,若大于则交换父子地位,继续向上调整
注:由于堆是完全二叉树,一个父亲最多有两个孩子,所以父亲的下标应该是孩子的下标减一再除以2,即parent=(child-1)/2;
//向上调整
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent= (child - 1) / 2;}else{break;}}
}6>删除根部数据:
思路:先交换根部数据和最后一个数据,再删除根部数据,同时将最后一个数据向下调整以保证删除后的堆仍为小堆
//删除堆顶数据(根位置)
void HPPop(HP* ph)
{assert(ph);Swap(&ph->a[0], &ph->a[ph->size - 1]);ph->size--;AdjustDown(ph->a, ph->size, 0);
}7>向下调整数据:
**思路:先找左右孩子中较小的那个孩子,与父亲相比,若父亲大于孩子,则交换父子地位,继续向下调整
注:由于堆是完全二叉树,一个父亲最多有两个孩子,所以左孩子的下标应该是父亲的下标乘以2再加1,即child=parent*2+1;
**画图解释
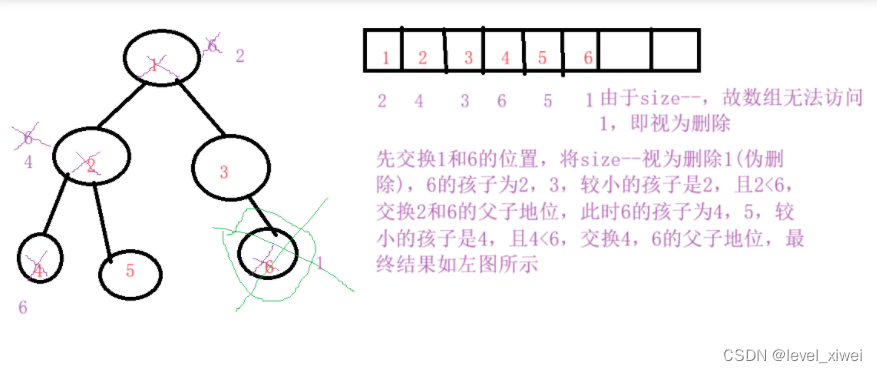
**代码实现
//向下调整
void AdjustDown(HeapDataType* a, int size, int parent)
{//默认左孩子小int child = parent * 2 + 1;while (child < size){//找左右孩子中小的那一个if ((child+1) < size && a[child+1] < a[child]){child ++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}(4)堆的应用
1>堆排序
1.1)思路:注:降序:建小堆,升序建大堆
将数组中的元素建堆,交换最后的数据与首位数据,并进行向下调整,让size--,循环操 作,直至完成排序
1.2)时间复杂度:O(N*log N)


1.3)画图解释:
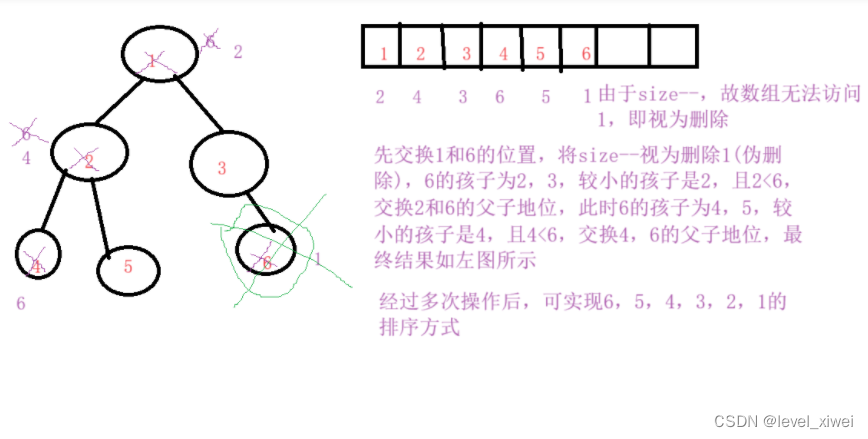
1.4)代码实现
void HeapSort(int* a, int size)
{//将数组建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}int end = size - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}2>TOP_K(以求前K个最大的数据为例)
2.1)定义:求出数据中前K个最大的数据(或前K个最小的数据)
2.2)思路:
思路一:创建一个含N个节点的大堆,PopK次,即可获取前K个最大的数据
弊端:当N非常大时,在创建节点时需要占用大量的内存
思路二:建一个含K个节点的小堆,将剩余的N-K个数据与堆顶数据相比,若大于堆顶数据则入 堆进行向下调整,否则进行下一个比较
注:思路二更优,效率高
2.3)代码实现
void TOP_K(int* a,int n,int k)
{//在文件中读取数据const char* fp = "data.txt";FILE* fout = fopen(fp, "r");if (fout == NULL){perror("fopen fail");return;}//读取前K个数据for (int i = 0; i < k; i++){fscanf(fout,"%d", &a[i]);}//建小堆for (int i = (k-1-1)/2;i>=0;i--){AdjustDown(a, k, i);}//将剩余的n-k个数据于堆顶数据相比int x = 0;while (fscanf(fout,"%d",&x)!=EOF){if (a[0]<x){a[0] = x;AdjustDown(a, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", a[i]);}printf("\n");
}
2.4)数据验证
思路:将N的节点的数据模上N,是他们处于小于N的状态,在随机挑K个数据将他们调大于N,若在选出来的K个数据为大于N的数据,则说明该程序执行的是选取前K个最大的数据的指令
二.二叉树的链式结构(以二叉链表为例)
注:在二叉树的实现中多用递归来达到一层一层向下查找的目的(所以读者需要熟练掌握递归的相关知识)
1.定义:用链表表示一颗二叉树,即用链表表示元素之间的逻辑关系
2.二叉树节点的定义:该节点内存储的数据,指向左孩子的指针,指向右孩子的指针
typedef int BTNodeData;
typedef struct BinaryTreeNode
{BTNodeData val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;3.二叉树的创建(根据前序遍历来创建二叉树):
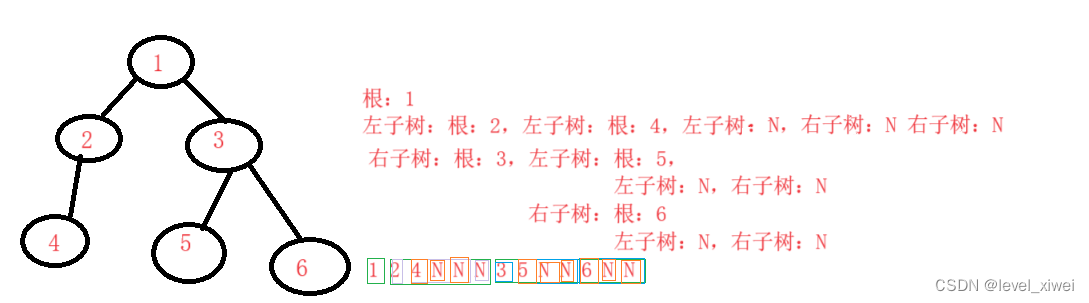
以数组abd##e#h##cf##g##构建二叉树
1>思路:1)若当前数据为#,则返回NULL;
2)否则开辟一个二叉树节点root,将该数据赋给val,给左,右孩子赋值,通过调用函数递 归实现
2>代码实现:
//创建二叉树
BTNode* BTCreate(BTNodeData* a, int* pi)
{if (a[*pi] == ‘#’){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = a[*pi];(*pi)++;root->left = BTCreate(a,pi);root->right = BTCreate(a, pi);return root;
}4.二叉树的前序遍历:
1>访问顺序:根,左子树,右子树
2>思路:如果根为空,打印N,什么都不返回;否则先打印根的值,再调用该函数,将左子树的地址作为参数,然后调用该函数,将右子树的地址作为参数,利用递归实现前序遍历
3>代码实现
//前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}5.二叉树的中序遍历
1>访问顺序:左子树,根,右子树
2>思路:与前序遍历类似
3>代码实现
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}6.二叉树的后序遍历
1>访问顺序:左子树,右子树,根
2>思路:与前序遍历类似
3>代码实现
//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}7.二叉树的层序遍历
1>思路:利用队列,让上一层的节点先入队列,在删除他们时,带进去下一层,若节点为空不进队列
2>代码实现:
//层序遍历
void BTLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->val);//当节点不为空时入队列if (front->left){QueuePush(&q, front->left);}if(front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q);
}
8.二叉树的节点个数
1>思路:1)如果根节点为空,返回0;
2)否则返回左子树的节点数+右子树的节点数+1(利用递归法实现左右子树节点数的计算)
2>代码实现:
//二叉树节点个数
int BTSize(BTNode* root)
{if (root == NULL){return 0;}return BTSize(root->left) + BTSize(root->right) + 1;
}
9.二叉树的叶子节点个数
1>思路:1)如果根为空,返回0;
2)如果左右孩子均为空,返回1;
3)否则返回左子树叶子数+右子树叶子数(利用递归实现左右子树叶子数的计算)
2>代码实现:
//二叉树叶子节点个数
int BTLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BTLeafSize(root->left) + BTLeafSize(root->right);
}10.二叉树第K层节点个数
1>思路:1)如果根为空返回0;
2)如果k==1,返回1;
3)否则返回左子树的k-1层+右子树的k-1层
注:将树一层一层向下压,直至出现两种特殊情况
2>代码实现:
//二叉树第K层节点个数
int BTLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTLevelKSize(root->left, k - 1) + BTLevelKSize(root->right, k - 1);
}11.二叉树查找值为X的节点
1>思路:1)若根为空,返回空;
2)若根的值等于待查找数据,返回根的地址;
3)否则查找左子树是否有值为X的节点若有返回该节点的地址,否则查找右子树是否有值 为X的节点若有返回该节点的地址,若左右子树均没有是否有值为X的节点,则返回空
2>代码实现:
//二叉树查找值为X的节点
BTNode* BTFind(BTNode* root, BTNodeData x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}//比较左子树是否有节点值为xBTNode* ret1 = BTFind(root->left, x);if (ret1!=NULL){return ret1;}//比较右子树是否有节点值为xBTNode* ret2 = BTFind(root->right, x);if (ret2 != NULL){return ret2;}//左右子树中均未找到值为x的节点return NULL;
}12.树的高度
1>思路:1)若根为空,返回0;
2)否则记录并分别求左右子树的高度,哪个值更大哪个即为树的高度
注:每次都需记录所求的树的高度,否则会出现走到上一层忘了下一层的情况,导致反复求某棵树高度的情况
2>代码实现:
//二叉树的高度
int BTHeight(BTNode* root)
{if (root == NULL){return 0;}int HeightLeft = BTHeight(root->left)+1;int HeightRight = BTHeight(root->right)+1;return HeightLeft > HeightRight ? HeightLeft : HeightRight ;
}13.二叉树的销毁
1>思路:用后序遍历的思想先销毁左右子树,再销毁根(若先销毁根,销毁根后,无法找到左右子树)
2>代码实现
//二叉树的销毁
void BTDestory(BTNode* root)
{if (root == NULL)return;BTDestory(root->left);BTDestory(root->right);free(root);}14.判断二叉树是否为完全二叉树
1>思路:无论节点是否为空都入队列,当检查到第一个空节点时,开始遍历后面的节点看是否有非空节点,若有,则不是完全二叉树,否则是完全二叉树
2>代码实现
//二叉树是否为完全二叉树
bool BTComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//若第一个空如队列,跳出循坏,开始遍历看之后是否有非空节点的存在if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//遍历,看是否有非空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}相关文章:

二叉树顺序结构及链式结构
一.二叉树的顺序结构 1.定义:使用数组存储数据,一般使用数组只适合表示完全二叉树,此时不会有空间的浪费 注:二叉树的顺序存储在逻辑上是一颗二叉树,但是在物理上是一个数组,此时需要程序员自己想清楚调整…...

【Python】pandas连续变量分箱
路过了学校花店 荒野到海边 有一种浪漫的爱 是浪费时间 徘徊到繁华世界 才发现你背影 平凡得特别 绕过了城外边界 还是没告别 爱错过了太久 反而错得完美无缺 幸福兜了一个圈 🎵 林宥嘉《兜圈》 import pandas as pd import numpy as np from sklearn.model_selecti…...

Qt 打卡小程序总结
1.Qt::Alignment(枚举类型)用于指定控件或文本的对齐方式 Qt::AlignLeft:左对齐。Qt::AlignRight:右对齐。Qt::AlignHCenter:水平居中对齐。Qt::AlignTop:顶部对齐。Qt::AlignBottom:底部对齐。…...

【qt】标准项模型
标准项模型 一.使用标准型项模型1.应用场景2.界面拖放3.创建模型4.配套模型5.视图设置模型6.视图属性的设置 二.从文件中拿到数据1.文件对话框获取文件名2.创建文件对象并初始化3.打开文件对象4.创建文本流并初始化5.读取文本流6.关闭文件7.完整代码 三.为模型添加数据1.自定义…...
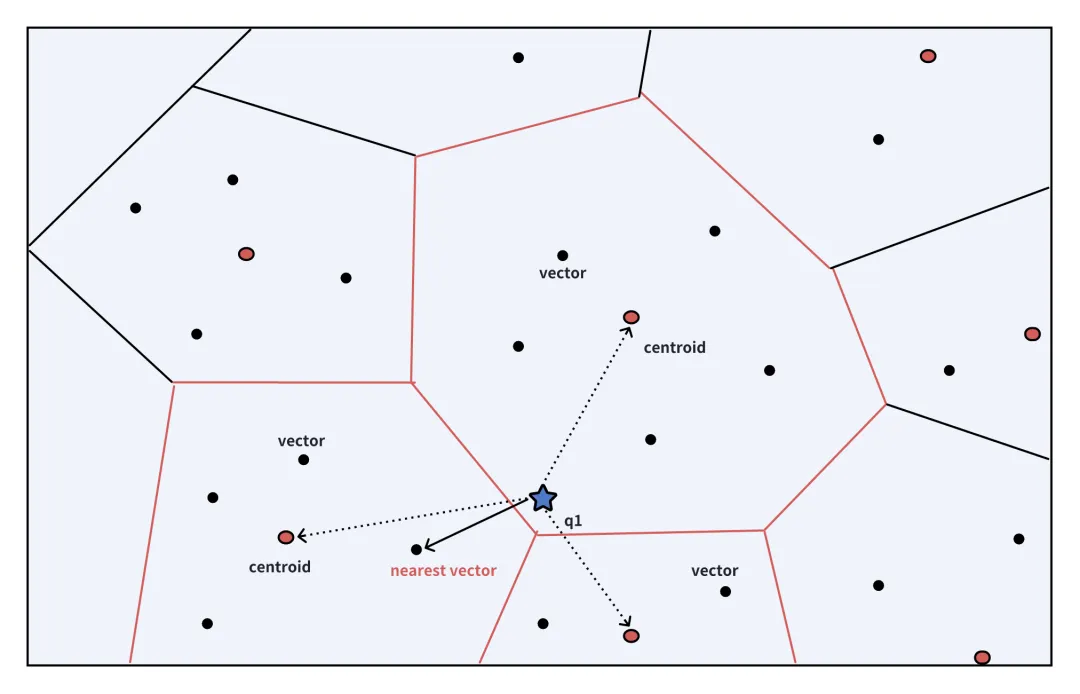
一文深度剖析 ColBERT
近年来,向量搜索领域经历了爆炸性增长,尤其是在大型语言模型(LLMs)问世后。学术界开始重点关注如何通过扩展训练数据、采用先进的训练方法和新的架构等方法来增强 embedding 向量模型。 在之前的文章中,我们已经深入探…...
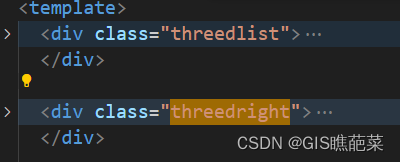
css左右滚动互不影响
想实现左右都可以滚动,且互不影响。 只需要再左边的css里面 .threedlist {cursor: pointer;width: 280px;position: fixed;height: 100vh; /* 定义父容器高度 */overflow-y: auto; /* 只有在内容超过父容器高度时才出现滚动条 */} 如果想取消滚动条样式 .threedli…...

【linux-uboot移植-mmc及tftp启动-IMX6ULL】
目录 1. uboot简介2. 移植前的基本介绍:2.1 环境系统信息: 3. 初次编译4. 烧录编译的u-boot4.1 修改网络驱动 5. 通过命令启动linux内核5.1 通过命令手动启动mmc中的linux内核5.1.1 fatls mmc 1:15.1.2 fatload mmc 1:1 0x80800000 zImage5.1.3 fatload mmc 1:1 0x8…...
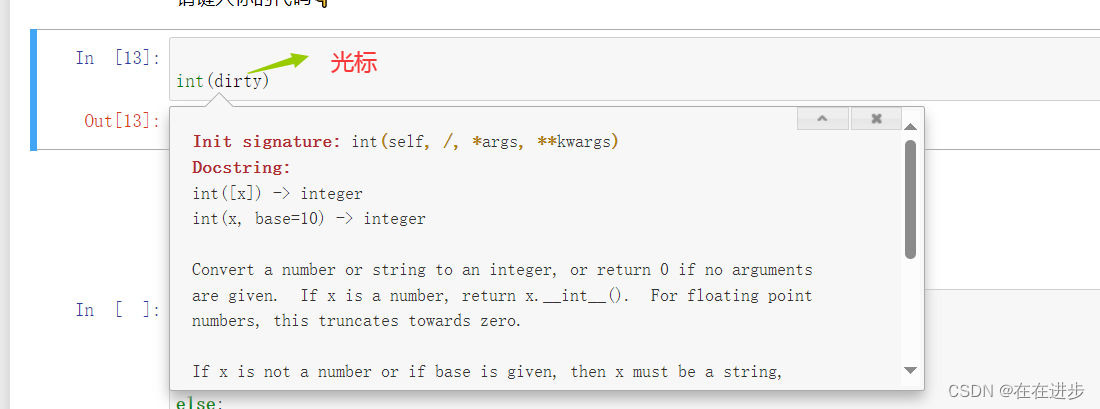
Python-温故知新
1快速打开.ipynb文件 安装好anaconda后,在需要打开notebook的文件夹中, shift键右键——打开powershell窗口——输入jupyter notebook 即可在该文件夹中打开notebook的页面: 2 快速查看函数用法 光标放在函数上——shift键tab 3......

绿联NAS DXP系列发布:内网穿透技术在私有云的应用分析
5月23日,绿联科技举行了“新一代存储方式未来已来”发布会,发布了绿联NAS私有云DXP系列(包括两盘位到八盘位的九款新品)以及由绿联科技自研的全新NAS系统UGOS Pro。此次绿联发布的DXP系列九款产品,共有两盘位、四盘位、…...

力扣:242. 有效的字母异位词
242. 有效的字母异位词 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。 注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。 示例 1: 输入: s "anagram", t "nagaram"…...
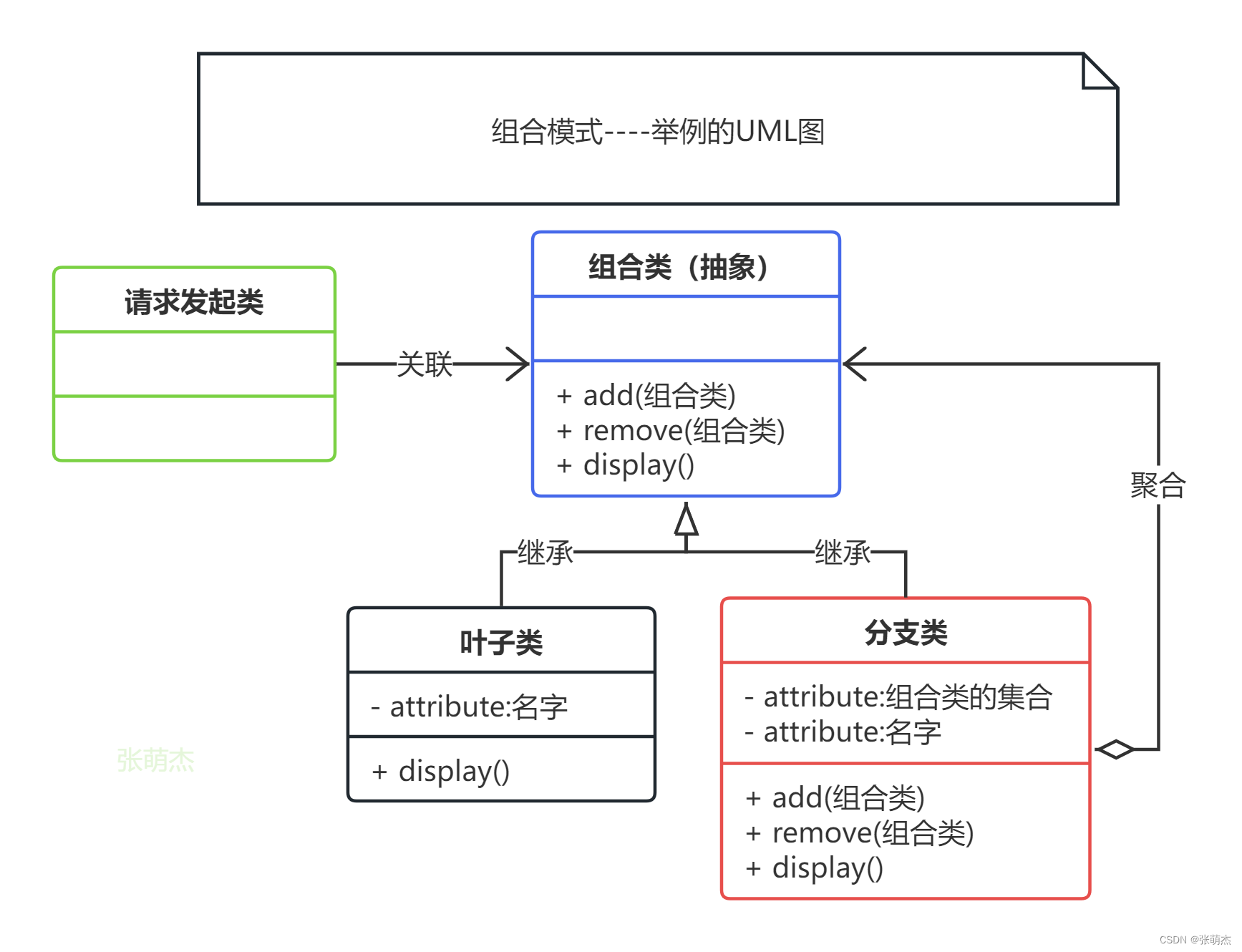
设计模式14——组合模式
写文章的初心主要是用来帮助自己快速的回忆这个模式该怎么用,主要是下面的UML图可以起到大作用,在你学习过一遍以后可能会遗忘,忘记了不要紧,只要看一眼UML图就能想起来了。同时也请大家多多指教。 组合模式(Composit…...
)
MyBatis面试题(Mybaits的优点、缺点、适用场合、与Hibernate有哪些不同)
一、Mybaits的优点: 1、基于 SQL 语句编程,相当灵活,不会对应用程序或者数据库的现有设计造成任 何影响,SQL 写在 XML里,解除 sql与程序代码的耦合,便于统一管理;提供 XML 标签,支持…...

python写接口性能测试
import time import requestsdef measure_response_time(api_url):try:start_time time.time()response requests.get(api_url, timeout10) # 设置超时时间为10秒end_time time.time()response_time end_time - start_timeprint(f"接口 {api_url} 的响应时间为&#…...

《暮色将尽》跨越世纪的历程,慢慢走向并完善自我
《暮色将尽》跨越世纪的历程,慢慢走向并完善自我 戴安娜阿西尔(1917-2019),英国知名文学编辑、作家。著有《暮色将尽》《昨日清晨》《未经删节》《长书当诉》等。 曾嵘 译 文章目录 《暮色将尽》跨越世纪的历程,慢慢走…...

python-鸡兔同笼问题:已知鸡和兔的总头数与总脚数。求笼中鸡和兔各几只?
【问题描述】典型的鸡兔同笼问题。 【输入形式】输入总头数和总脚数两个实数:h,f 【输出形式】笼中鸡和兔的个数:x,y 【样例输入】16 40 【样例输出】鸡12只,兔4只 【样例说明】输入输出必须保证格式正确。…...

【NumPy】关于numpy.transpose()函数,看这一篇文章就够了
🧑 博主简介:阿里巴巴嵌入式技术专家,深耕嵌入式人工智能领域,具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍:分享嵌入式开发领域的相关知识、经验、思考和感悟,欢迎关注。提供嵌入式方向…...
什么是住宅IP代理?为什么需要家庭 IP 代理
家庭代理 IP 允许您选择特定位置(国家、城市或移动运营商)并作为代理上网该区域的真实用户。住宅代理 IP 可以定义为保护用户免受一般网络流量影响的中介。它们在隐藏您的 IP 地址的同时充当缓冲区。住宅代理 IP 是服务提供商分配给用户的替代 IP 地址。…...

Java方法的重载
Java方法的重载 前言一、为什么要有重载代码示例问题 代码示例 二、重载的使用代码示例 三、重载的规则针对同一个类代码示例 前言 推荐一个网站给想要了解或者学习人工智能知识的读者,这个网站里内容讲解通俗易懂且风趣幽默,对我帮助很大。我想与大家分…...
RabbitMQ 消息队列安装及入门
市面常见消息队列中间件对比 技术名称吞吐量 /IO/并发时效性(类似延迟)消息到达时间可用性可靠性优势应用场景activemq万级高高高简单易学中小型企业、项目rabbitmq万级极高(微秒)高极高生态好(基本什么语言都支持&am…...

K8S认证|CKA题库+答案| 14. 排查故障节点
14、排查集群中的故障节点 CKA v1.29.0模拟系统免费下载试用: 百度网盘:https://pan.baidu.com/s/1vVR_AK6MVK2Jrz0n0R2GoQ?pwdwbki 题目: 您必须在以下Cluster/Node上完成此考题: Cluster …...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
