LeetCode 1542.找出最长的超赞子字符串:前缀异或和(位运算)
【LetMeFly】1542.找出最长的超赞子字符串:前缀异或和(位运算)
力扣题目链接:https://leetcode.cn/problems/find-longest-awesome-substring/
给你一个字符串 s 。请返回 s 中最长的 超赞子字符串 的长度。
「超赞子字符串」需满足满足下述两个条件:
- 该字符串是
s的一个非空子字符串 - 进行任意次数的字符交换后,该字符串可以变成一个回文字符串
示例 1:
输入:s = "3242415" 输出:5 解释:"24241" 是最长的超赞子字符串,交换其中的字符后,可以得到回文 "24142"
示例 2:
输入:s = "12345678" 输出:1
示例 3:
输入:s = "213123" 输出:6 解释:"213123" 是最长的超赞子字符串,交换其中的字符后,可以得到回文 "231132"
示例 4:
输入:s = "00" 输出:2
提示:
1 <= s.length <= 10^5s仅由数字组成
解题方法:前缀和+哈希表+位运算
回文串有两种情况:
- 所有字符都出现了偶数次、
- 有且仅有一个字符出现了奇数次。
也就是说我们只用关心每个字符出现次数是奇数还是偶数即可。因此我们可以使用一个数 m a s k mask mask, m a s k mask mask的第 i i i位表示数字 i i i出现次数是否为奇数次。
加入在 m a s k mask mask的基础上又出现了 i i i,则新的 m a s k mask mask的计算公式为:
mask ^= 1 << i。
我们只需要遍历一遍字符串,并且使用哈希表,哈希表 m a [ m a s k ] ma[mask] ma[mask]为前面所有数字结果为 m a s k mask mask的第一次出现位置。则遍历过程中有“
- 若当前 m a s k mask mask出现过,则这两次出现位置之间所有字符都出现了偶数次,满足回文串要求;
- 若当前 m a s k mask mask变化一位后在哈希表中存在,则这两次出现位置之间的字符串只有一个出现了奇数次,满足回文串要求。
遍历结束,算法结束。
- 时间复杂度 O ( l e n ( s ) × C ) O(len(s)\times C) O(len(s)×C),其中 C C C是字符个数,这里 C = 10 C=10 C=10
- 空间复杂度 O ( min { l e n ( s ) , 2 C } ) O(\min\{len(s), 2^C\}) O(min{len(s),2C})
AC代码
C++
class Solution {
public:int longestAwesome(string s) {int mask = 0, ans = 1;unordered_map<int, int> ma;ma[0] = -1;for (int i = 0; i < s.size(); i++) {mask ^= (1 << (s[i] - '0'));if (ma.count(mask)) {ans = max(ans, i - ma[mask]);}else {ma[mask] = i;}// 一个奇数次字符for (int j = 0; j < 10; j++) {int mask2 = mask ^ (1 << j);if (ma.count(mask2)) {ans = max(ans, i - ma[mask2]);}}}return ans;}
};
Python
class Solution:def longestAwesome(self, s: str) -> int:mask, ans = 0, 1ma = {0: -1}for i in range(len(s)):mask ^= 1 << (ord(s[i]) - ord('0'))if mask in ma:ans = max(ans, i - ma[mask])else:ma[mask] = ifor j in range(10):mask2 = mask ^ (1 << j)if mask2 in ma:ans = max(ans, i - ma[mask2])return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/139077950
相关文章:
)
LeetCode 1542.找出最长的超赞子字符串:前缀异或和(位运算)
【LetMeFly】1542.找出最长的超赞子字符串:前缀异或和(位运算) 力扣题目链接:https://leetcode.cn/problems/find-longest-awesome-substring/ 给你一个字符串 s 。请返回 s 中最长的 超赞子字符串 的长度。 「超赞子字符串」需…...

LLM企业应用落地场景中的问题概览
三个问题 AI思维快速工具:需要对接LLM的API、控制幻觉、管理知识库。POC验证四个难点 私有化部署的环境:包括网络和服务器环境。交互友好意想不到的情况方向选择:让客户做目标和方向的选择问题 一、RAG 多跳问题 通常发生在报告编写的数据整理环节,比如要从一堆报表中找…...
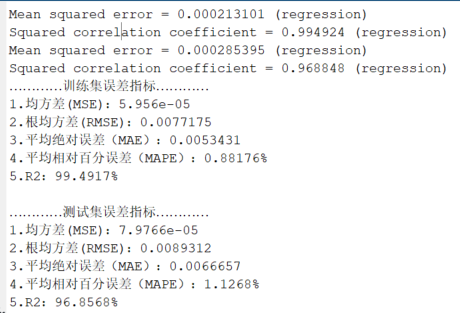
基于灰狼优化算法优化支持向量机(GWO-SVM)时序预测
代码原理及流程 基于灰狼优化算法优化支持向量机(GWO-SVM)的时序预测代码的原理和流程如下: 1. **数据准备**:准备时序预测的数据集,将数据集按照时间顺序划分为训练集和测试集。 2. **初始化灰狼群体和SVM模型参数…...

C++中获取int最大与最小值
不知道大家有没有遇到过这种要求:“返回值必须是int,如果整数数超过 32 位有符号整数范围 [−2^31, 2^31 − 1] ,需要截断这个整数,使其保持在这个范围内。例如,小于 −2^31 的整数应该被固定为 −2^31 ,大…...
学习通高分免费刷课实操教程
文章目录 概要整体架构流程详细步骤云上全平台登录步骤小结 概要 我之前提到过一个通过浏览器的三个脚本就可以免费高分刷课的文章,由于不方便拍视频进行实操演示,然后写下了这个实操教程,之前的三个脚本划到文章末尾 整体架构流程 整体大…...

缓存降级
当Redis缓存出现问题或者无法正常工作时,需要有一种应对措施,避免直接访问数据库而导致整个系统瘫痪。缓存降级就是这样一种机制。 主要的缓存降级策略包括: 本地缓存降级 当Redis缓存不可用时,可以先尝试使用本地进程内缓存,如Guava Cache或Caffeine等。这样可以减少对Redis…...
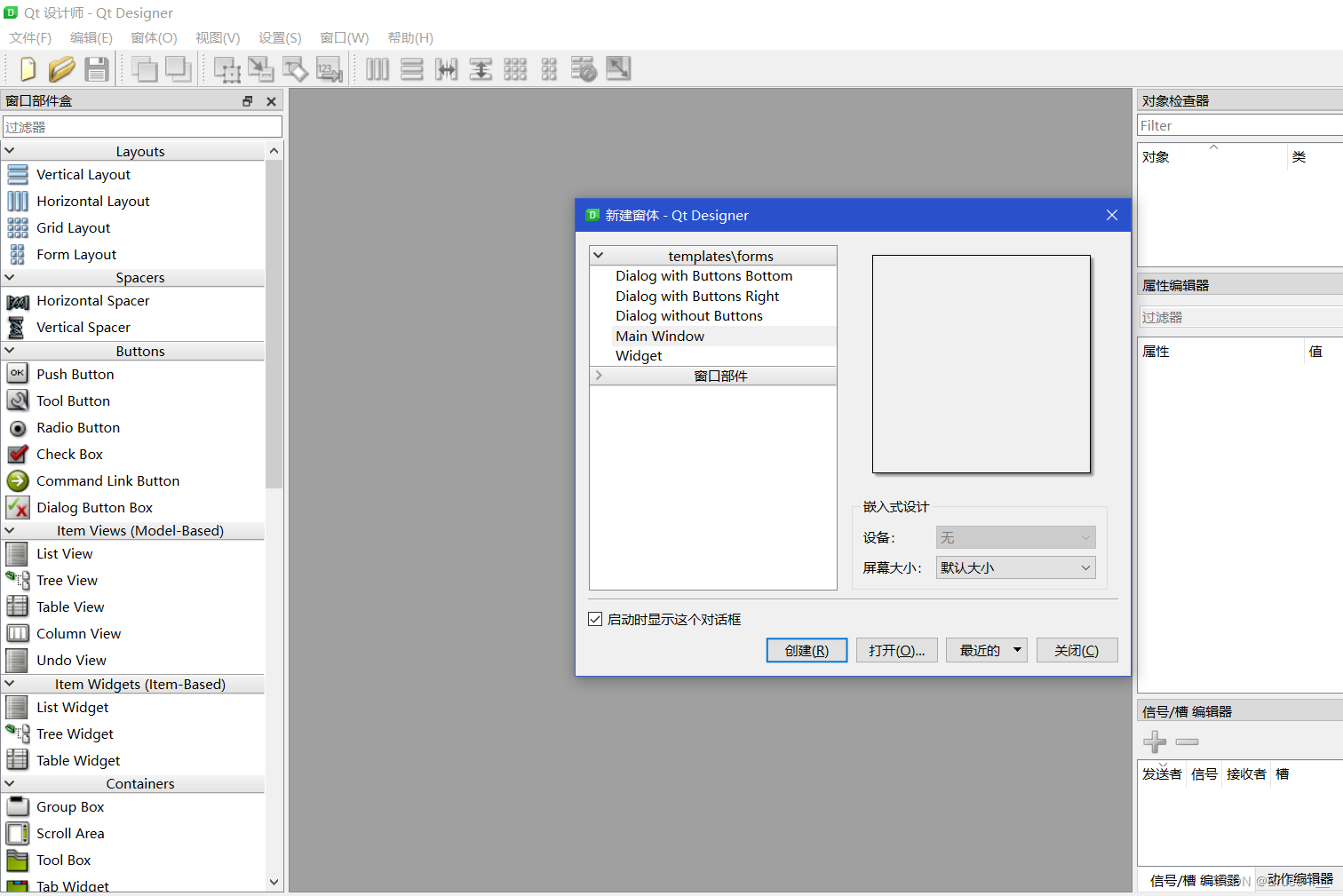
PyQt6--Python桌面开发(32.QMenuBar菜单栏控件)
QMenuBar菜单栏控件 选择Main Window...

golang创建式设计模式---工厂模式
创建式设计模式—工厂模式 目录导航 创建式设计模式---工厂模式1)什么是工厂模式2)使用场景3)实现方式4)实践案例5)优缺点分析 1)什么是工厂模式 工厂模式(Factory Method Pattern)是一种设计模式,旨在创建对象时,将对象的创建与使用进行分离。通过定义…...

高精度定位平板主要应用在哪些领域
高精度定位平板是一种集成了高精度定位技术和强大计算能力的设备,能够提供亚米级甚至厘米级的定位精度。其应用领域广泛,涵盖测绘、精准农业、工程建设、地理信息系统(GIS)、公共安全等多个方面。这种设备凭借其高精度和耐用性&am…...

conda使用常用命令
Conda是一个非常常用的Python包管理器,也是Anaconda Python发行版的一部分。它可以帮助用户安装、更新、卸载Python包,以及管理Python虚拟环境。在这篇博客中,我们将总结一些常用的Conda命令及其用法。 安装和更新Conda 在使用Conda之前&…...
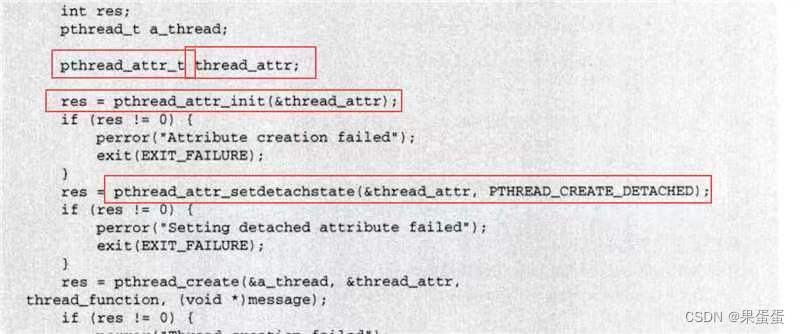
22-LINUX--多线程and多进程TCP连接
一.TCP连接基础知识 1.套接字 所谓套接字(Socket),就是对网络中不同主机上的应用进程之间进行双向通信的端点的抽象。一个套接字就是网络上进程通信的一端,提供了应用层进程利用网络协议交换数据的机制。从所处的地位来讲,套接字上联应用进程…...

像素级创意:深入浅出PixelCNN图像合成技术
参考 https://arxiv.org/pdf/1601.06759 https://blog.csdn.net/zcyzcyjava/article/details/126559327 需要熟悉熵的一些理论、和极大释然估计等价于最小化交叉熵等知识 1. pixelcnn建模方法 pixelcnn做生成模型的想必都有耳闻。它是一种自回归模型,什么是自回归…...

MyBatisPlus使用流程
引入依赖 <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.4</version> </dependency> 版本号根据需要选取 在实体类上加注解声明,表信息 根据数…...

爬虫技术升级:如何结合DrissionPage和Auth代理插件实现数据采集
背景/引言 在大数据时代,网络爬虫技术已经成为数据收集的重要手段之一。爬虫技术可以自动化地从互联网上收集数据,节省大量人力和时间成本。然而,当使用需要身份验证的代理服务器时,许多现有的爬虫框架并不直接支持代理认证。这就…...
go 微服务框架kratos错误处理的使用方法及原理探究
通过go语言原生http中响应错误的实现方法,逐步了解和使用微服务框架 kratos 的错误处理方式,以及探究其实现原理。 一、go原生http响应错误信息的处理方法 处理方法: ①定义返回错误信息的结构体 ErrorResponse // 定义http返回错误信息的…...

AI播客下载:Dwarkesh Podcast(关于AI的深度访谈)
Dwarkesh Podcast 是由 Dwarkesh Patel 主持的播客,专注于深度访谈和探讨各种复杂且有趣的话题。该播客在业界获得了极高的评价,被认为是对话和思想交流的平台。 Dwarkesh Podcast 的内容涵盖了多个领域,包括经济学、哲学以及科技等。例如&am…...

C++11function包装器的使用
类模板std::function是一种通用、多态的函数包装。std::function的实例可以对任何可以调用的目标实体进行存储、 复制和调用操作。这些目标实体包括普通函数、Lambda表达式、函数指针、以及其他函数对象等。std::function对象是对 C中现有的可调用实体的一种类型安全的包裹&…...

Vue3判断变量和对象不为null和undefined
Vue3判断变量和对象不为null和undefined 一、判断变量二、判断对象 一、判断变量 在 Vue 3 中,你可以使用 JavaScript 提供的常规方式来检查变量是否不为 null 和不为 undefined。你可以分别使用严格不等运算符 ! 来比较变量是否不为 null 和不为 undefined。以下是…...
C++进阶:C++11(列表初始化、右值引用与移动构造移动赋值、可变参数模版...Args、lambda表达式、function包装器)
C进阶:C11(列表初始化、右值引用与移动构造移动赋值、可变参数模版…Args、lambda表达式、function包装器) 今天接着进行语法方面知识点的讲解 文章目录 1.统一的列表初始化1.1{}初始化1.2 initializer_listpair的补充 2.声明相关关键字2.1a…...

Vue.js Promise 与 async/await 的比较
在现代 Web 开发中,异步操作是不可避免的。在处理异步数据获取时,开发人员通常会使用 Promise 或 async/await。虽然两者都可以实现相同的功能,但它们在代码风格、可读性和错误处理等方面有所不同。本文将对这两种方法进行比较,并…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
