2021牛客OI赛前集训营-提高组(第三场)T2交替
2021牛客OI赛前集训营-提高组(第三场)
题目大意
一个长度为nnn的数组aaa,每秒都会变成一个长度为n−1n-1n−1的新数组a′a'a′,其变化规则如下
- 如果当前数组aaa的大小nnn为偶数,则对于新数组a′a'a′的每一个位置i(1≤i<n)i(1\leq i<n)i(1≤i<n),ai′=ai+ai+1a'_i=a_i+a_{i+1}ai′=ai+ai+1
- 如果当前数组aaa的大小nnn为奇数,则对于新数组a′a'a′的每一个位置i(1≤i<n)i(1\leq i<n)i(1≤i<n),ai′=ai−ai+1a'_i=a_i-a_{i+1}ai′=ai−ai+1
最终数组经过n−1n-1n−1秒后变为一个数字,求这个数字对109+710^9+7109+7取模后的结果。
题解
通过打表可以发现,当nnn为偶数时,aia_iai对答案的贡献为(−1)t×Cn/2−1t(-1)^t\times C_{n/2-1}^{t}(−1)t×Cn/2−1t,其中t=⌊i−12⌋t=\lfloor\dfrac{i-1}{2}\rfloort=⌊2i−1⌋。
如果nnn为偶数,则直接用上面的规律来求即可。如果nnn为奇数,那么操作一次,将nnn变为偶数,再用上面的规律来求即可。
当然,考场上可以直接用打表发现的规律,但学习要严谨,所以下面给出证明。
用多项式a1x+a2x2+⋯+anxna_1x+a_2x^2+\cdots+a_nx^na1x+a2x2+⋯+anxn表示当前的状态,用xix^ixi的系数表示当前第iii个位置的值。
- 对于长度为偶数变为奇数的操作,相当于原来的多项式乘上(1+1x)(1+\dfrac 1x)(1+x1)
- 对于长度为奇数变为偶数的操作,相当于原来的多项式乘上(1−1x)(1-\dfrac 1x)(1−x1)
那么nnn每减去2,则多项式乘上(1−1x2)(1-\dfrac{1}{x^2})(1−x21)。
对于偶数的nnn,多项式要乘上(1−1x2)n/2−1(1+1x)=(1−Cn/2−111x2+Cn/2−121x4−⋯)(1+1x)(1-\dfrac{1}{x^2})^{n/2-1}(1+\dfrac 1x)=(1-C_{n/2-1}^1\dfrac{1}{x^2}+C_{n/2-1}^2\dfrac{1}{x^4}-\cdots)(1+\dfrac 1x)(1−x21)n/2−1(1+x1)=(1−Cn/2−11x21+Cn/2−12x41−⋯)(1+x1)。最后的答案就是xxx的系数。
我们考虑如何求xxx的系数。对于最初多项式中的xix^ixi,
- 如果iii是奇数,则xix_ixi可以和(−1)tCn/2−1t1xi−1(-1)^tC_{n/2-1}^{t}\dfrac{1}{x^{i-1}}(−1)tCn/2−1txi−11相乘来得到xxx的项
- 如果iii是偶数,则xix_ixi可以和(−1)tCn/2−1t1xi−2×1x(-1)^tC_{n/2-1}^{t}\dfrac{1}{x^{i-2}}\times \dfrac 1x(−1)tCn/2−1txi−21×x1相乘来得到xxx的项
其中t=⌊i−12⌋t=\lfloor\dfrac{i-1}{2}\rfloort=⌊2i−1⌋。
那么就可以得到开头的结论。
时间复杂度为O(n)O(n)O(n)。
code
#include<bits/stdc++.h>
using namespace std;
int n;
long long ans=0,a[100005],jc[100005],ny[100005];
long long mod=1000000007;
long long mi(long long t,long long v){if(!v) return 1;long long re=mi(t,v/2);re=re*re%mod;if(v&1) re=re*t%mod;return re;
}
long long C(int x,int y){return jc[x]*ny[y]%mod*ny[x-y]%mod;
}
int main()
{scanf("%d",&n);jc[0]=1;for(int i=1;i<=n;i++) jc[i]=jc[i-1]*i%mod;ny[n]=mi(jc[n],mod-2);for(int i=n-1;i>=0;i--) ny[i]=ny[i+1]*(i+1)%mod;for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}if(n==1){printf("%d",(a[1]%mod+mod)%mod);return 0;}if(n%2==1){--n;for(int i=1;i<=n;i++){a[i]=(a[i]-a[i+1]+mod)%mod;}}for(int i=1;i<=n;i++){int x=(n-1)/2,y=(i-1)/2;if(y&1) ans=(ans-C(x,y)*a[i]%mod+mod)%mod;else ans=(ans+C(x,y)*a[i]%mod+mod)%mod;}printf("%lld",ans);return 0;
}
相关文章:
T2交替)
2021牛客OI赛前集训营-提高组(第三场)T2交替
2021牛客OI赛前集训营-提高组(第三场) 题目大意 一个长度为nnn的数组aaa,每秒都会变成一个长度为n−1n-1n−1的新数组a′aa′,其变化规则如下 如果当前数组aaa的大小nnn为偶数,则对于新数组a′aa′的每一个位置i(1≤…...

论文投稿指南——中文核心期刊推荐(金融)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...
【独家】)
华为OD机试 - 不等式(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:不等式题…...
90后老板用低代码整顿旅行社,创2000万年收,他是怎么做到的?(真实)
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

Apache Dubbo 存在反序列化漏洞(CVE-2023-23638)
漏洞描述 Apache Dubbo 是一款轻量级 Java RPC 框架 该项目受影响版本存在反序列化漏洞,由于Dubbo在序列化时检查不够全面,当攻击者可访问到dubbo服务时,可通过构造恶意请求绕过检查触发反序列化,执行恶意代码 漏洞名称Apache …...

【YOLO】YOLOv8训练自定义数据集(4种方式)
YOLOv8 出来一段时间了,继承了分类、检测、分割,本文主要实现自定义的数据集,使用 YOLOV8 进行检测模型的训练和使用 YOLOv8 此次将所有的配置参数全部解耦到配置文件 default.yaml,不再类似于 YOLOv5,一部分在配置文件…...

linux重置root用户密码
重置root密码 法一:rd.break 第 1 步:重启系统编辑内核参数 第 2 步:找到 linux 这行,在此行末尾空格后输入rd.break (End键也可直接进入行尾) 成功后显示页面为: 第 3 步:查看。…...
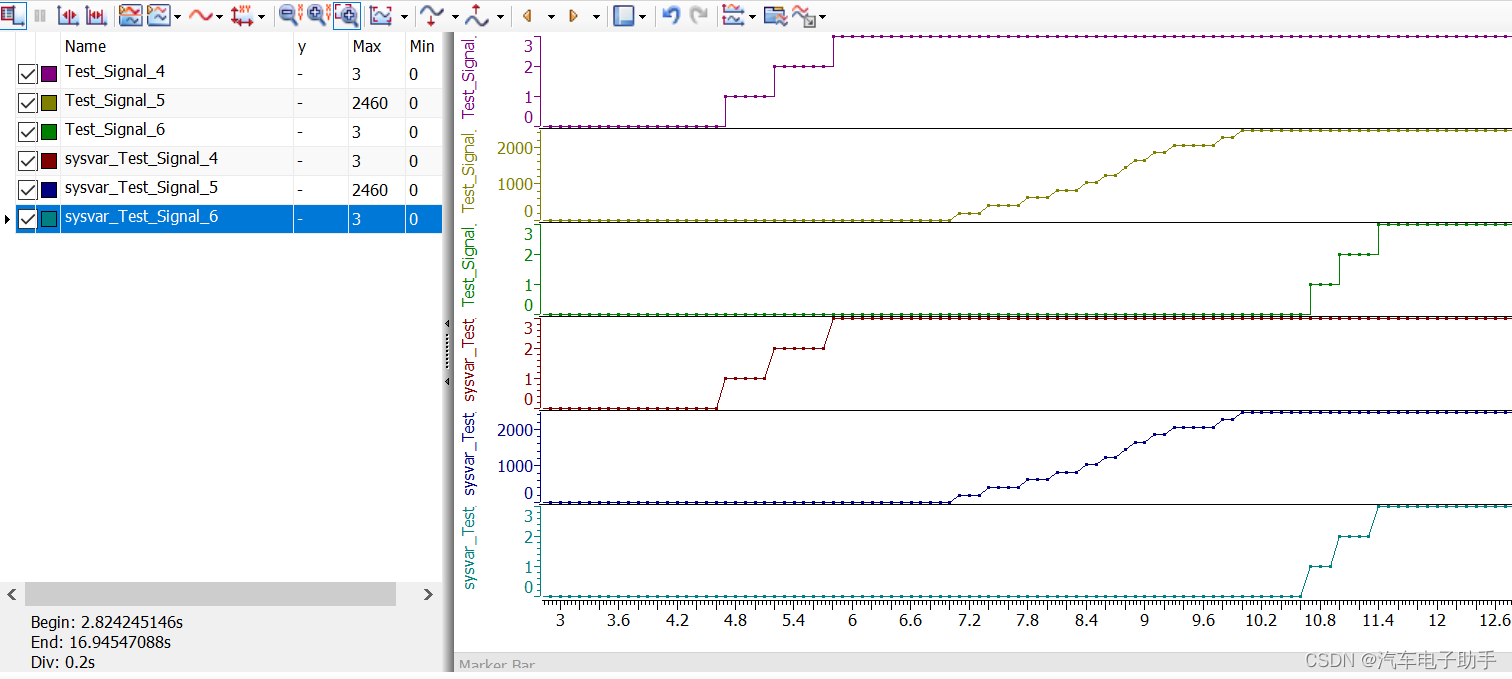
【DBC专题】-10-CAN DBC转换C语言代码Demo_接收Rx报文篇
案例背景(共15页精讲): 该篇博文将告诉您,CAN DBC转换C语言代码Demo,只需传递对应CAN信号关联参数,无需每个信号"左移"和"右移",并举例介绍:在CANoe/Canalyzer中CAPL中的应用ÿ…...

AtCoder292 E 思维
题意: 给定一副n(n≤3000)n(n\leq 3000)n(n≤3000)个顶点,mmm条有向边的图,可以在图中添加有向边,求添加的最少边数,使得这副图满足:如果顶点aaa到顶点bbb有边,顶点bbb到ccc右有边,…...

20230309英语学习
What Is Sleep Talking? We Look at the Science 为什么人睡觉会说梦话?来看看科学咋说 Nearly everyone has a story about people talking in their sleep.Though it tends to be more common in children, it can happen at any age:A 2010 study in the jour…...
CAD转换PDF格式怎么弄?教你几种方法轻松搞定!
CAD是从事与艺术创作相关等行业的打工人们必需的工作软件,可以用来完成建筑设计图、设计图纸等。在日常的工作中,一些伙伴经常需要传输图纸给合作方来完成探讨。但是CAD图纸需要使用专业软件才能打开,这就给文件传送带来了一定的困难。而且传…...

AtCoder 259E LCM
题意: 以唯一分解形式给出nnn个数: aipi,1ei,1pi,2ei,2...pi,tei,ta_{i}p_{i,1}^{e_{i,1}}p_{i,2}^{e_{i,2}}...p_{i,t}^{e_{i,t}} aipi,1ei,1pi,2ei,2...pi,tei,t 现在可以将某个数改为111,求所有改法中,有多少个…...

MQTT协议-取消订阅和取消订阅确认
MQTT协议-取消订阅和取消订阅确认 客户端向服务器取消订阅 取消订阅的前提是客户端已经通过CONNECT报文连接上服务器,并且订阅了一个主题 UNSUBSCRIBE—取消订阅 取消订阅的报文同样是由固定报头可变报头有效载荷组成 固定报头由两个字节组成,第一个…...

90后小伙,用低代码“整顿”旅游业,年入2000万,他是怎么做到的?
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

C51---PWM 脉冲宽度调制
1.PWM:脉冲宽度调制,它是通过一系列脉冲宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码。也就是说通过调节占空比的变化来调节信号、能量等的变化,占空比就是指在一个周期内,信号处于…...

毕业设计 基于51单片机WIFI智能家居系统设计
基于51单片机WIFI智能家居系统设计1、毕业设计选题原则说明(重点)2、项目资料2.1 系统框架2.2 系统功能3、部分电路设计3.1 STC89C52单片机最小系统电路设计3.2 ESP8266 WIFI电路设计3.3 DHT11温湿度传感器电路设计4、部分代码展示4.1 LCD12864显示字符串…...
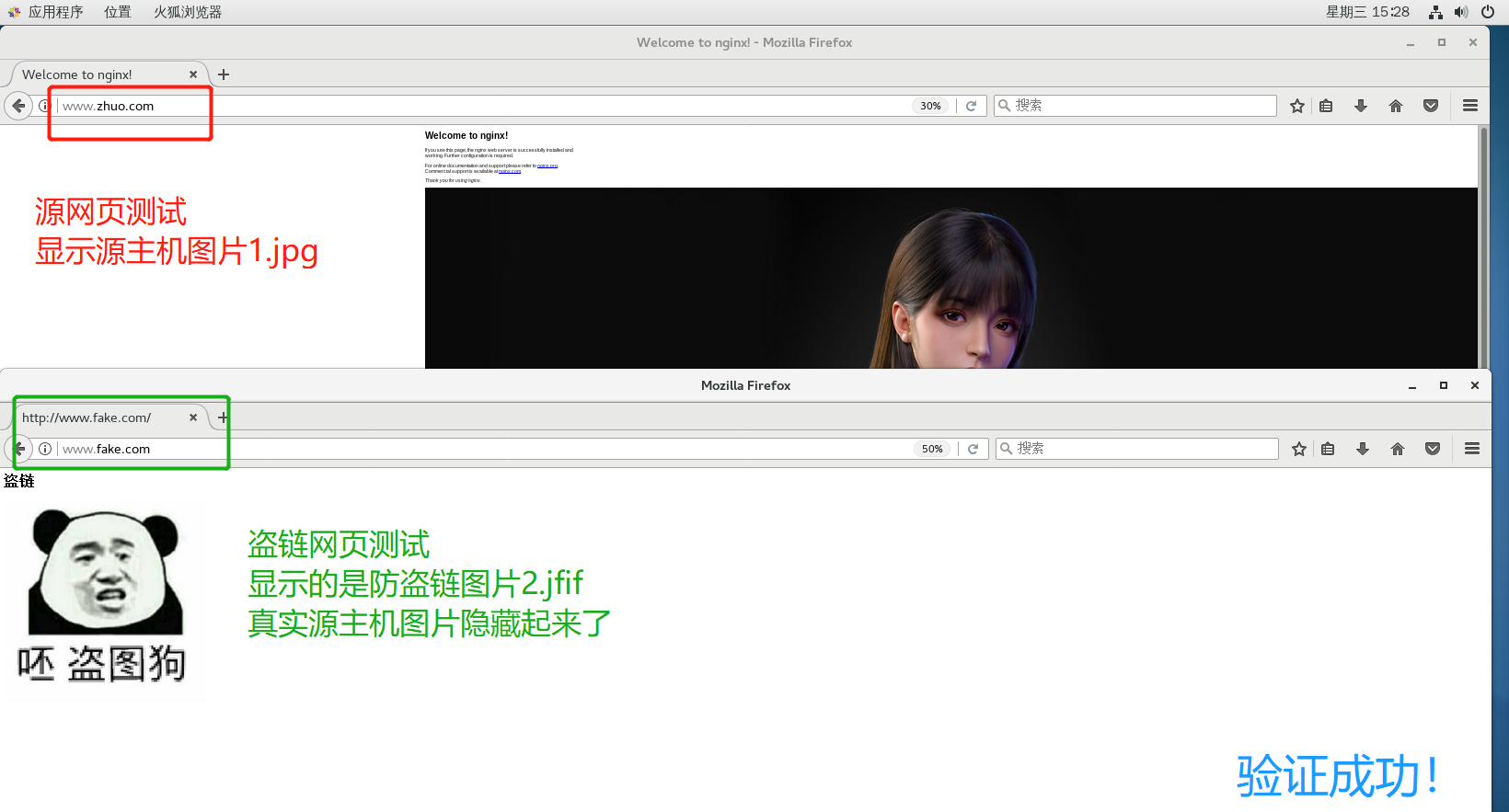
Nginx服务优化措施与配置防盗链
目录 一.优化Nginx的相关措施 二.隐藏/查看版本号 三.修改用户与组 四.设置缓存时间 五.日志切割脚本 六.设置连接超时控制连接访问时间 七.开启多进程 八.配置网页压缩 九.配置防盗链 1.配置web源主机(192.168.79.210 www.zhuo.com) 1.1 安装…...

Java 某厂面试题真题合集
哈喽~大家好,这篇来看看Java 某厂面试题真题合集。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Spr…...

很特别的5G市场,5.75亿部手机,却有11亿5G用户,这是怎么了?
中国在5G商用方面已取得了巨大的成绩,这是毋庸置疑的,不过近期公布的一份数据却相当特别,5G手机用户数为5.75亿,而开通了5G套餐的用户数却已超过11亿,这数据对比有点意思。中国在5G商用方面推进很快,建成的…...

go modules
文章目录1. 简介示例1. 示例——同一项目2. 示例——不同项目3. 示例——添加远程模块依赖库1. 简介 go module是Go1.11版本之后官方推出的版本管理工具,并且从Go1.13版本开始,go module将是Go语言默认的依赖管理工具。到今天Go1.14版本推出之后Go modu…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
