AtCoder 259E LCM
题意:
以唯一分解形式给出nnn个数:
ai=pi,1ei,1pi,2ei,2...pi,tei,ta_{i}=p_{i,1}^{e_{i,1}}p_{i,2}^{e_{i,2}}...p_{i,t}^{e_{i,t}} ai=pi,1ei,1pi,2ei,2...pi,tei,t
现在可以将某个数改为111,求所有改法中,有多少个不同的lcm(a1,a2,...,an)lcm(a_{1},a_{2},...,a_{n})lcm(a1,a2,...,an)
Solution:
由于涉及lcmlcmlcm,不妨将各个数改写成这样的形式
a1=2e1,13e1,25e1,3.......an=2en,13en,25en,3....a_{1}=2^{e_{1,1}}3^{e_{1,2}}5^{e_{1,3}}.... \\ ... \\ a_{n}=2^{e_{n,1}}3^{e_{n,2}}5^{e_{n,3}}.... a1=2e1,13e1,25e1,3.......an=2en,13en,25en,3....
那么
lcm(a1,a2,...,an)=2max{e1,1,e2,1,...,en,1}3max{e1,2,e2,2,...,en,2}...lcm(a_{1},a_{2},...,a_{n})=2^{max\{e_{1,1},e_{2,1},...,e_{n,1}\}}3^{max\{e_{1,2},e_{2,2},...,e_{n,2}\}}... lcm(a1,a2,...,an)=2max{e1,1,e2,1,...,en,1}3max{e1,2,e2,2,...,en,2}...
考虑删掉一个数的影响,即将某个数aka_{k}ak设为1
ak=203050....a_{k}=2^{0}3^{0}5^{0}.... ak=203050....
对于一个质数底pk,ip_{k,i}pk,i,如果他的幂是nnn个数里同底的唯一最高次的话,删去他才会对lcmlcmlcm有影响,如果两个数的唯一最高次的底的构成是一样的,那么对这两个数的操作是等价的,于是考虑存在多少个不同的构成的数。
由于唯一分解内,不同的构成的乘积一定不同,于是可以用他们的乘积代表他们的构成,用一个map来指示这个底的最高次
底x的最高次幂=map1[x]
底x有多少个最高次幂=tot[x]
把他们的乘积加入set后,set的大小就是答案
#include<iostream>
#include<vector>
#include<cstdlib>
#include<numeric>
#include<unistd.h>
#include<queue>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<set>
#include<map>
#include<stack>
#include<utility>
#include<cctype>
#include<cassert>
#include<thread>
#include<bitset>
using namespace std;using ll=long long;
const int N=2e5+5,inf=0x3fffffff;
const long long INF=0x3fffffffffffffff,mod=1e11+7;int n;
vector<int>p[N],e[N];
map<int,int>map1,tot;int main() {#ifdef stdjudgefreopen("in.txt","r",stdin);auto TimeFlagFirst=clock();#endifstd::ios::sync_with_stdio(false);std::cin.tie(nullptr);cin>>n;for(int i=1;i<=n;i++) {int t; cin>>t;while(t--) {int pp,ee; cin>>pp>>ee;if(!map1.count(pp)) map1[pp]=ee,tot[pp]=1;else if(ee>map1[pp]) map1[pp]=ee,tot[pp]=1;else if(ee==map1[pp]) tot[pp]++;p[i].emplace_back(pp);e[i].emplace_back(ee);}}set<ll>set1;for(int i=1;i<=n;i++) {ll val=1;for(int j=0;j<p[i].size();j++) {if(e[i][j]==map1[p[i][j]]&&tot[p[i][j]]==1) val=val*p[i][j]%mod;}set1.insert(val);}cout<<set1.size()<<endl;#ifdef stdjudgefreopen("CON","r",stdin);std::cout<<std::endl<<"耗时:"<<std::clock()-TimeFlagFirst<<"ms"<<std::endl;std::cout<<std::flush;system("pause");#endifreturn 0;
}
相关文章:

AtCoder 259E LCM
题意: 以唯一分解形式给出nnn个数: aipi,1ei,1pi,2ei,2...pi,tei,ta_{i}p_{i,1}^{e_{i,1}}p_{i,2}^{e_{i,2}}...p_{i,t}^{e_{i,t}} aipi,1ei,1pi,2ei,2...pi,tei,t 现在可以将某个数改为111,求所有改法中,有多少个…...

MQTT协议-取消订阅和取消订阅确认
MQTT协议-取消订阅和取消订阅确认 客户端向服务器取消订阅 取消订阅的前提是客户端已经通过CONNECT报文连接上服务器,并且订阅了一个主题 UNSUBSCRIBE—取消订阅 取消订阅的报文同样是由固定报头可变报头有效载荷组成 固定报头由两个字节组成,第一个…...
90后小伙,用低代码“整顿”旅游业,年入2000万,他是怎么做到的?
热爱旅游的92年成都小伙猴哥,大学毕业后开了一家旅行社,主要从事川藏、云南定制游服务。 从今年春节开始,国内各地旅游业开始复苏,向旅行社打电话咨询的人越来越多。 旅游的人多是好事,也是一种烦恼,因为…...

C51---PWM 脉冲宽度调制
1.PWM:脉冲宽度调制,它是通过一系列脉冲宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码。也就是说通过调节占空比的变化来调节信号、能量等的变化,占空比就是指在一个周期内,信号处于…...

毕业设计 基于51单片机WIFI智能家居系统设计
基于51单片机WIFI智能家居系统设计1、毕业设计选题原则说明(重点)2、项目资料2.1 系统框架2.2 系统功能3、部分电路设计3.1 STC89C52单片机最小系统电路设计3.2 ESP8266 WIFI电路设计3.3 DHT11温湿度传感器电路设计4、部分代码展示4.1 LCD12864显示字符串…...
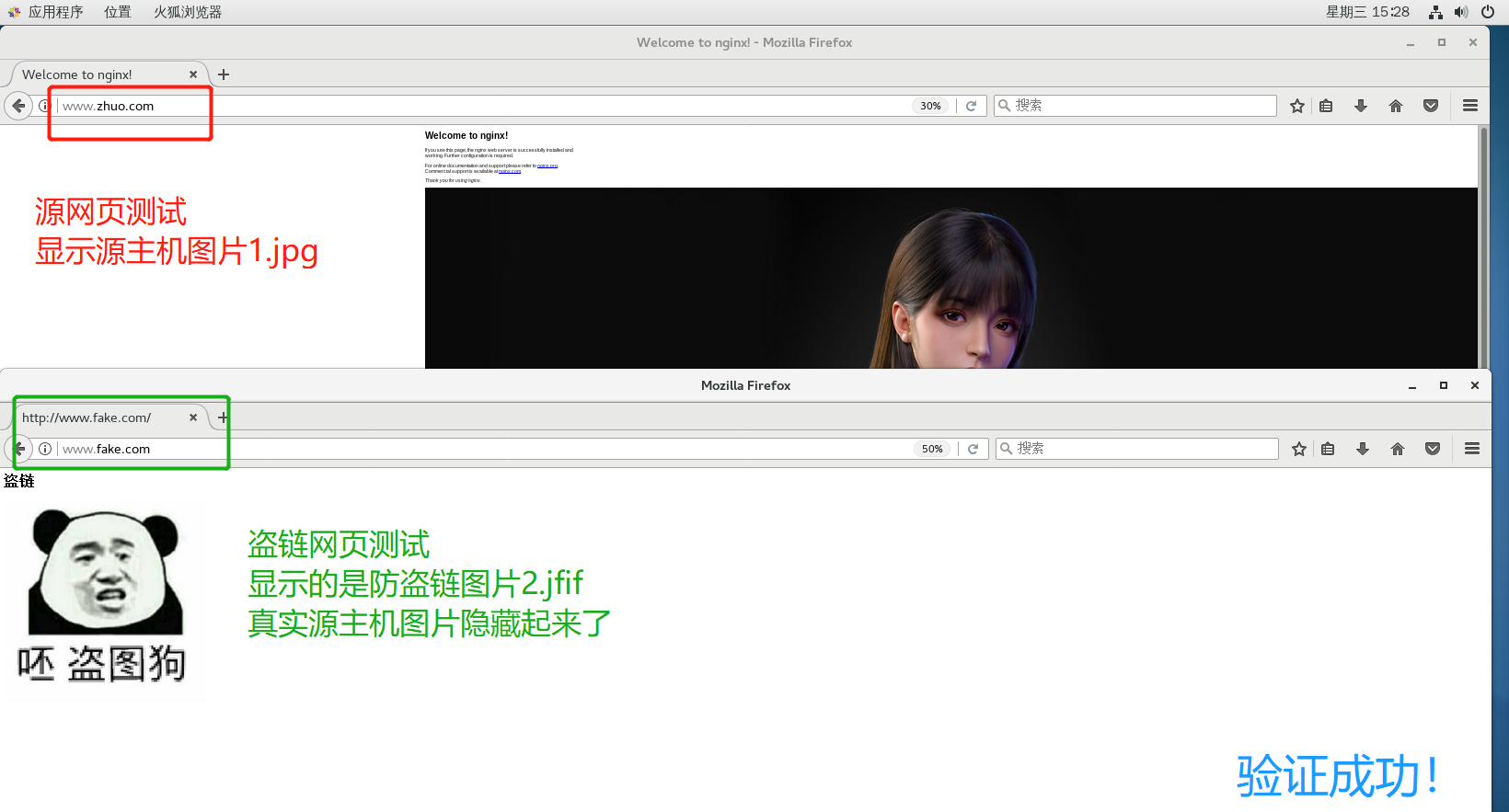
Nginx服务优化措施与配置防盗链
目录 一.优化Nginx的相关措施 二.隐藏/查看版本号 三.修改用户与组 四.设置缓存时间 五.日志切割脚本 六.设置连接超时控制连接访问时间 七.开启多进程 八.配置网页压缩 九.配置防盗链 1.配置web源主机(192.168.79.210 www.zhuo.com) 1.1 安装…...

Java 某厂面试题真题合集
哈喽~大家好,这篇来看看Java 某厂面试题真题合集。 🥇个人主页:个人主页 🥈 系列专栏:【日常学习上的分享】 🥉与这篇相关的文章: Spr…...

很特别的5G市场,5.75亿部手机,却有11亿5G用户,这是怎么了?
中国在5G商用方面已取得了巨大的成绩,这是毋庸置疑的,不过近期公布的一份数据却相当特别,5G手机用户数为5.75亿,而开通了5G套餐的用户数却已超过11亿,这数据对比有点意思。中国在5G商用方面推进很快,建成的…...

go modules
文章目录1. 简介示例1. 示例——同一项目2. 示例——不同项目3. 示例——添加远程模块依赖库1. 简介 go module是Go1.11版本之后官方推出的版本管理工具,并且从Go1.13版本开始,go module将是Go语言默认的依赖管理工具。到今天Go1.14版本推出之后Go modu…...
Baklib客户故事:快递助手ERP
快递助手ERP以多平台多店铺订单管理为核心,集打单发货、商品、库存、采购、售后于一体,中小商家易上手的轻量级ERP,可以满足满足微商、自建商城、档口货源网、一件代发等不同类型客户的打单需求,通过开放平台API接口,自…...
MongoDB学习(java版)
MongoDB概述 结构化数据库 结构化数据库是一种使用结构化查询语言(SQL)进行管理和操作的数据库,它们的数据存储方式是基于表格和列的。结构化数据库要求数据预先定义数据模式和结构,然后才能存储和查询数据。结构化数据库通常…...

RK3568平台开发系列讲解(显示篇)什么是DRM
🚀返回专栏总目录 文章目录 一、DRM介绍二、DRM与framebuffer的区别沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍什么是DRM。 一、DRM介绍 DRM 是 Linux 目前主流的图形显示框架,相比FB架构,DRM更能适应当前日益更新的显示硬件。 比如FB原生不支…...

Python蓝桥杯训练:基本数据结构 [二叉树] 上
Python蓝桥杯训练:基本数据结构 [二叉树] 上 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 上一、前言二、有关二叉树理论基础1、二叉树的基本定义2、二叉树的常见类型3、二叉树的遍历方式三、有关二叉树的层序遍历的题目1、[二叉树的层序遍历](http…...
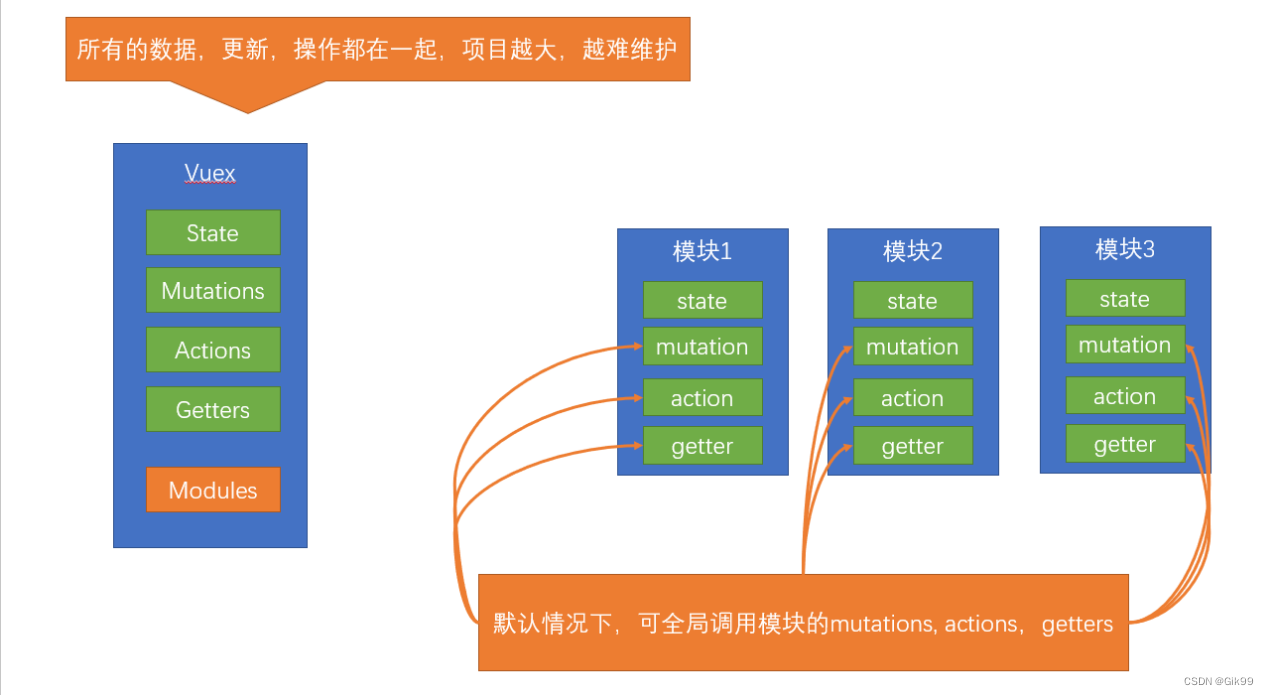
vuex基础之初始化功能、state、mutations、getters、模块化module的使用
vuex基础之初始化功能、state、mutations、getters、模块化module的使用一、Vuex的介绍二、初始化功能三、state3.1 定义state3.2 获取state3.2.1 原始形式获取3.2.2 辅助函数获取(mapState)四、mutations4.1 定义mutations4.2 调用mutations4.2.1 原始形式调用($store)4.2.2 辅…...

WebSphere中间件漏洞总结
WebSphere中间件漏洞总结 一、WebSphere简介 WebSphere为SOA(面向服务架构)环境提供软件,以实现动态的、互联的业务流程,为所有业务情形提供高度有效的应用程序基础架构。WebSphere是IBM的应用程序和集成软件平台,包含所有必要的中间件基础架构(包括服务器、服务和工具)…...

Unity之ASE实现影魔灵魂收集特效
前言 我们今天来实现一下Dota中的影魔死亡后,灵魂收集的特效。效果如下: 实现原理 1.先添加一张FlowMap图,这张图的UV是根据默认UV图,用PS按照我们希望的扭曲方向修改的如下图所示: 2.通过FlowMap图,我…...

半入耳式耳机运动会不会掉、佩戴超稳固的运动耳机推荐
现在越来越多的人开始意识到运动的重要性,用运动给身体增加一道“防护墙”是最好的生活方式了,不过,日复一日做着几乎相同的动作,难免索然无味,所以很多人都会选择在运动时戴上耳机听歌解闷,这时候也有不少…...
使用Tensorflow完成一个简单的手写数字识别
Tensorflow中文手册 介绍TensorFlow_w3cschool 模型结构图: 首先明确模型的输入及输出(先不考虑batch) 输入:一张手写数字图(28x28x1像素矩阵) 1是通道数 输出:预测的数字(1x10的one…...

OpenGL三种向着色器传递数据的方法 attributes,uniform,texture以及中间产物
(1)属性,使在顶点着色器中使用的变量,用于描述顶点的属性,如位置、颜色、法向量等,attributes通常用于描述每个顶点的属性,因此在顶点缓冲对象中存储,渲染的时候,openGL会…...

详解package.json和package-lock
详解package.json和package-lockpackage.json和package-lock.json作用首先要明确一点,package.json不会自动生成,需要我们使用 npm init 创建。package-lock.json是自动生成的,我们使用 npm install 安装包后就会自动生成。在我们执行 npm in…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
